0 引言
随着光伏发电技术的不断发展,三电平逆变器越来越多地受到关注,由于其开关管容量小、效率高,在工程中得到越来越多的应用[1]。但由于三电平逆变器的开关频率比较高,导致由于死区原因引起的逆变器并网电流谐波问题更加明显;另外由于控制作用和电网背景谐波引起的电网电流谐波也是导致并网电流谐波特性变差的重要因素。
针对电网电流谐波大等并网电流问题,业界提出了多种谐波抑制方案[2],包括采用谐振控制器的方法和死区补偿的方法等[3-4],其中谐振控制器能够对特定次的谐波进行无差跟踪和抑制,但对含有多次谐波的并网电流就需要并联多个谐振控制器进行抑制,这就增加了系统的复杂性[5];死区补偿方法的原理是通过抬高调制波幅值来消除死区带来的谐波影响,有一定的效果,但不明显[6]。
重复控制能够对周期性的误差信号起到很好的抑制作用,因此能够对多次谐波起到抑制作用,但由于重复控制对系统的作用有一定的延迟性,故动态性能比较差[7];而PI控制能够对基波信号有很好的跟踪性能,响应速度比较快,但稳态性能比较差。因此,采用PI+重复控制的控制策略不仅能够兼顾系统的快速性和稳定性,还能对并网电流的谐波起到很好的抑制作用,得到了广泛的应用[8-9]。
然而传统的PI+重复控制在PI和重复控制相互耦合之后,容易导致等效重复控制出现不稳定,针对该问题,有文章提出PI与重复控制进行加权平均的策略进行控制,但该策略的加权系数不容易确定且运行过程中时刻需要改变,相对比较麻烦[10]。也有文章提出利用针对各次谐波的谐振滤波器相加组成的补偿函数进行稳定性补偿[11],但补偿函数复杂,不易实现。
本文在传统的PI+重复控制的基础上,采用最常见的PI控制器进行补偿,不仅控制简单,参数容易整定,而且与传统的PI+重复控制构成双PI+重复控制系统(DPI+RC);在保证了传统PI+重复控制系统跟踪的快速性和准确性前提下,确保了系统的稳定性。因此,该控制方法更具实际工程意义。最后,通过仿真和试验测试,验证了该控制策略对谐波抑制的可行性与有效性。
1 三电平逆变器数学模型
三电平逆变器的主电路结构图如图1所示,功率桥采用T字形拓扑结构。其中L1为桥臂侧滤波电感,L2为网侧滤波电感,C为滤波电容,构成LCL型滤波器;i为桥臂电流,igrid为并网电流,ic为电容电流。
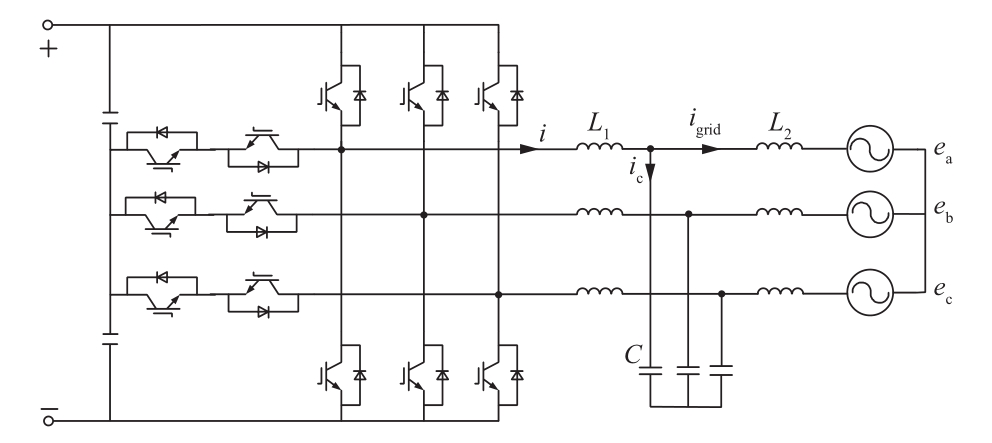
图1 三电平并网逆变器主电路图
Fig.1 Main circuit diagram of the three - level grid inverter
由上图可以得出逆变器交流侧简化结构图,如图2所示。
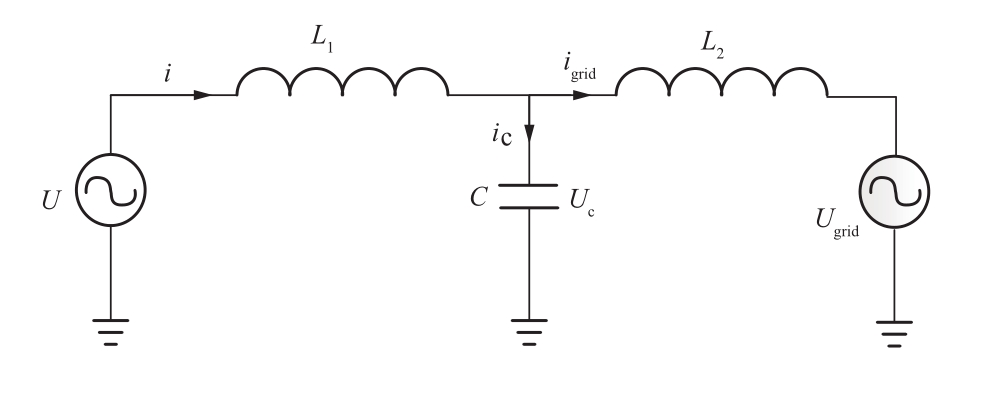
图2 逆变器交流侧简化结构图
Fig.2 Diagram of the relationship between inverter and grid structure
假设L1、L2及C均为理想元件,根据交流侧简化结构图可以得出下式,其中U为桥臂输出电压;由图2可以得出
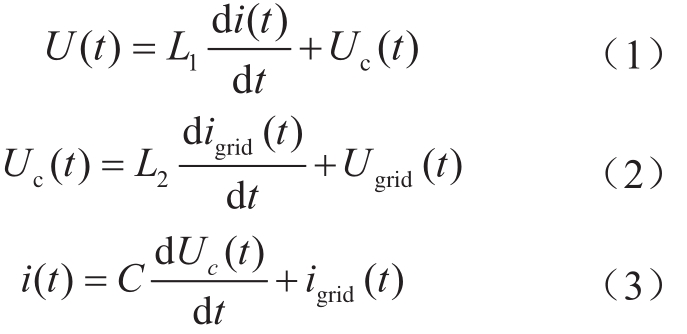
由式(1)、式(2)和式(3)可以得出并网电流和桥臂电压之间的传递函数
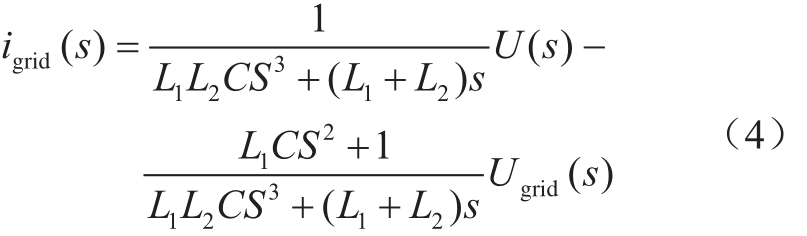
若把电网电压当作系统的干扰量,则可得到滤波器的输入电压到输出电流的传递函数
由式(4)可以看出,并网电流igrid跟Ugrid和U有关,即并网电流的谐波产生跟电网电压、电网背景谐波及逆变器控制输出的桥臂电压有关[12]。其中电网中经常含有5、7次谐波,进而导致并网电流中会含有一定的5、7次谐波;而由于逆变器调制中的死区效应等控制也会引起并网电流含有一定的谐波成分;针对该问题,提出了一种双PI+重复的控制方法对谐波进行抑制。
2 双PI+重复控制的谐波抑制及稳定性分析
2.1 重复控制原理及谐波抑制
重复控制是基于内模原理的一种控制方法,重复控制器结构如图3所示。
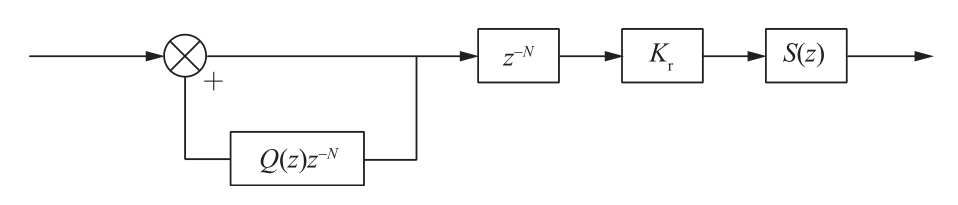
图3 重复控制器结构图
Fig.3 Structure diagram of repeat control
其内模是由延时时间为一个外部信号周期的延时环节经正反馈构成的。对于重复出现且频率是基波倍数的谐波信号,该内模的输出信号是输入信号的逐周期累加,其作用与积分环节相近,能够对输入的外部信号进行调节。当输入信号最终被调节为0时,该内模仍然会逐周期输出与上周期相同的控制信号,从而实现系统的零稳态误差跟踪。
式中,Kr为重复控制器增益;通常Q(z)为一低通滤波器或者一个小于1的常数;补偿环节S(z)一般情况下由补偿器Gc(z)和二阶低通滤波Hc(z)两部分组成。
令Q(z) = 0.95,S(z) =1,当Kr不同时,重复控制器的伯德图如图4所示,从图中可以看出,重复控制器在倍频次处的增益很大,所以重复控制器可以对倍频次谐波进行无差控制;而在频率点f = (50k+25)Hz,(k = 1,2,3…)处,该重复控制器相频曲线必然穿过(-2k+1)π,(k = 1,2,3…),从而产生稳定性问题,若要保证该环节稳定,需保证在这些频率点处的幅值增益应小于0 dB,由图4可知,当Kr增大到一定值,这些频率点处的幅值增益将会大于0 dB,所以为保证系统稳定,Kr的取值一般要求小于1。

图4 重复控制器伯德图
Fig.4 Bode diagram of repeat control
2.2 PI+重复控制原理及稳定性分析
2.2.1 PI+重复控制原理分析
重复控制能够对周期性的谐波成分进行无静差跟踪;但由于其包含延迟环节,所以重复控制器动态性能较差,传统的PI+重复控制采用的是PI与重复控制并联的控制策略。
图5为传统的PI+重复控制系统结构图,PI(z)为PI控制器,G(z)为被控对象,H(z)为反馈环节;PI控制器与重复控制器并联。
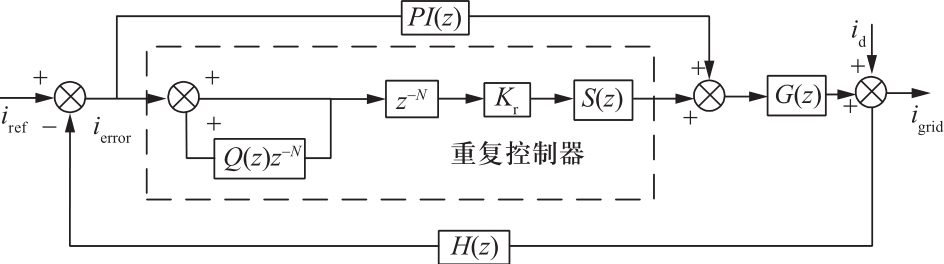
图5 PI+重复控制系统结构图
Fig.5 Structure diagram of PI + repeat control
PI+重复控制器的传递函数如下式
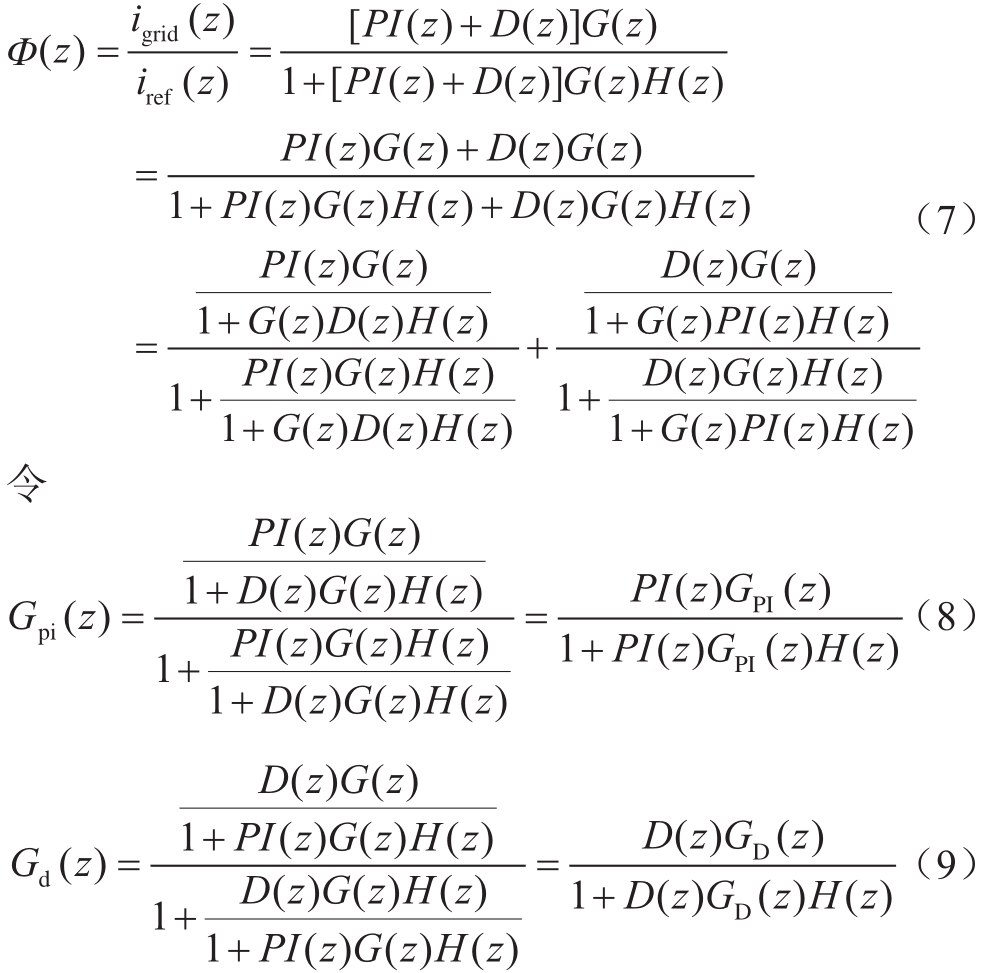
由上式推导可以得出,电流内环由Gpi(z)和Gd(z)组成,其中Gpi(z)等效为PI控制环,其等效控制对象为![]() 等效为重复控制闭环器,等效控制对象
等效为重复控制闭环器,等效控制对象![]() 且PI控制环和重复控制环有耦合。
且PI控制环和重复控制环有耦合。
2.2.2 PI+重复控制参数设计及稳定性分析
根据控制理论,只要复合控制的各子系统是稳定的,复合系统就是稳定的,故只要Gpi(z)和Gd(z)是稳定的,系统就是稳定的。
本文被控对象为LCL滤波器及相应的延迟环节,其LCL参数为:桥臂侧电感L1=170 μH,并网侧电感L2=20 μH,滤波电容C= 140 μF。
被控对象经过双线性变换后,传递函数为
其中,离散周期为100 μs。考虑到光伏逆变器主要抑制谐波为13次以下,故可取Hc(z)的截止频率为800 Hz,采用双线性变换离散化后的传递函数
首先在不考虑重复控制器作用情况下,重复控制器等效控制对象GD(z)的开环bode图如图6所示,由图可知该环节的幅值裕度为-1.81 dB,相位裕度为-18.2°,说明该等效控制对象本身不稳定。
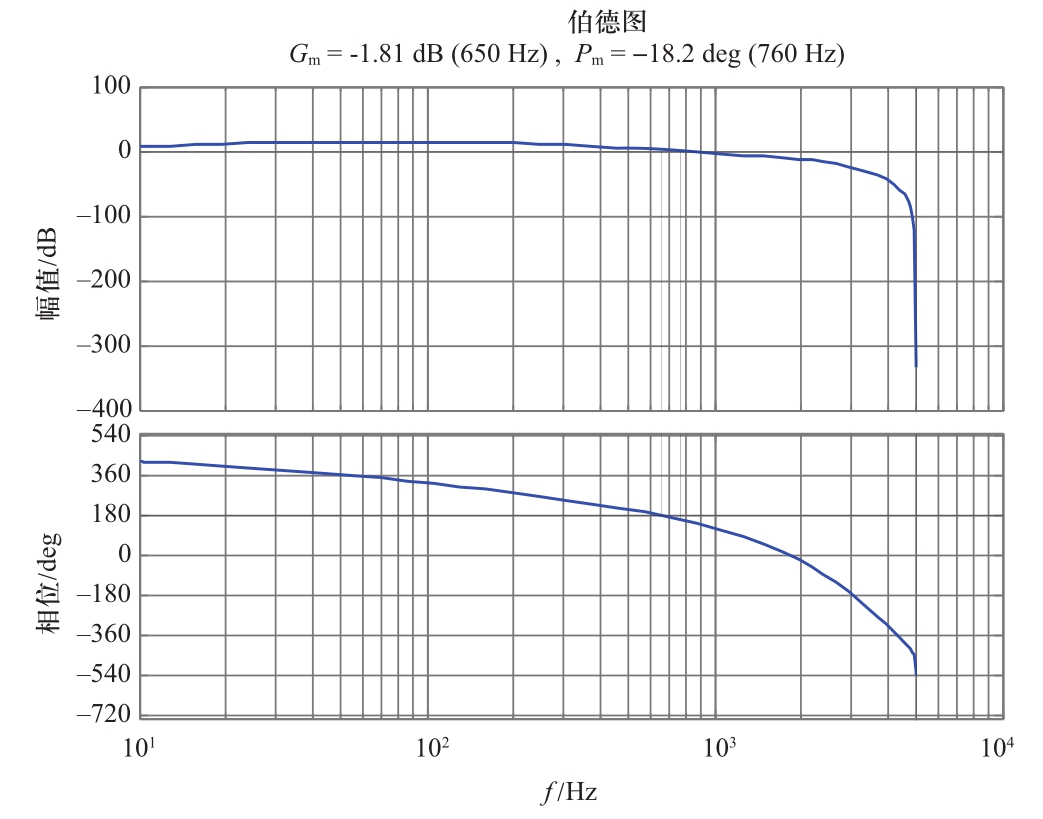
图6 补偿前等效控制对象bode图
Fig.6 Bode diagram of the equivalent control object before compensation
2.3 双PI+重复控制稳定性分析
针对传统PI+重复控制等效控制对象不稳定的问题,本文提出利用PI控制器进行补偿,原理图如图7所示;利用PI2补偿控制器的高频幅值衰减特性,使已补偿系统的截止频率下降,从而使系统获得足够的稳定裕度。
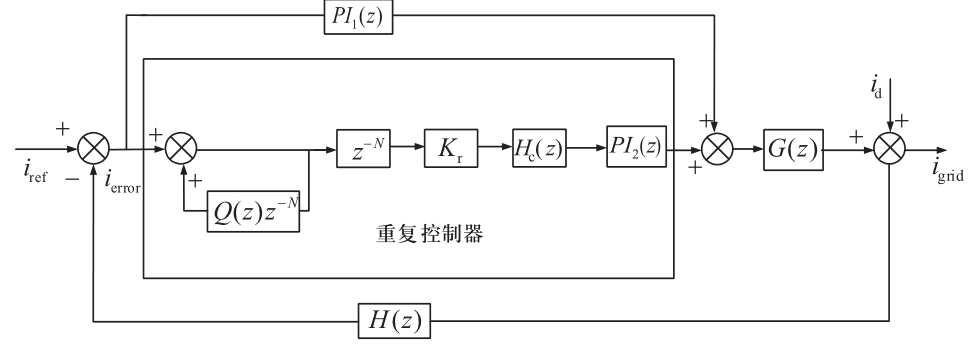
图7 双PI+重复控制原理图
Fig.7 Structure diagram of double PI + repeat control
在上述系统的基础上,此处取PI2进行补偿:![]() 离散化后传递函数
离散化后传递函数![]() 加入PI补偿后重复控制器等2效控制对象GD(z)的开环bode图如图8所示,由图可知,幅值裕度为12.1 dB,相位裕度为无穷,故该开环系统稳定。
加入PI补偿后重复控制器等2效控制对象GD(z)的开环bode图如图8所示,由图可知,幅值裕度为12.1 dB,相位裕度为无穷,故该开环系统稳定。
补偿后等效重复控制环Gd(z)的伯德图如图9所示,该系统幅值裕度为4.5 dB,相角裕度为47.2°;所以等效重复控制为稳定系统。另外,中低频段,在基频及倍频处,系统保持高增益;高频段,幅频特性能够快速衰减,以保证系统的稳定裕度。
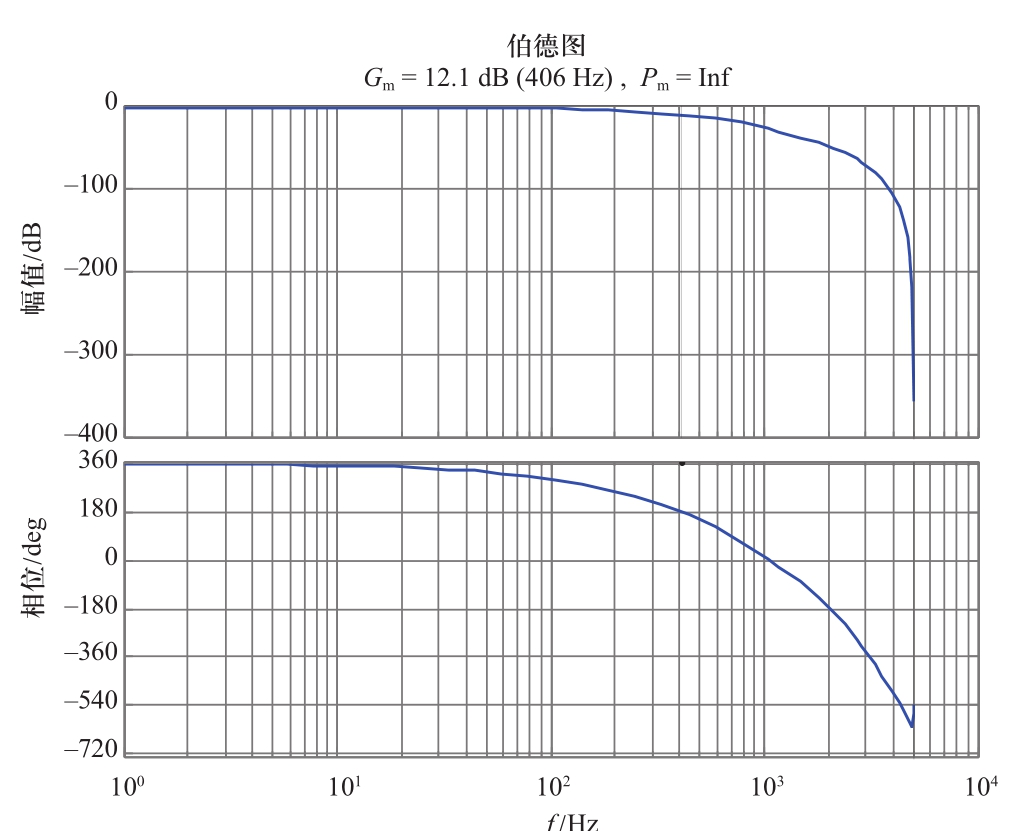
图8 补偿后等效控制对象bode图
Fig.8 Bode diagram of the equivalent control object after compensation
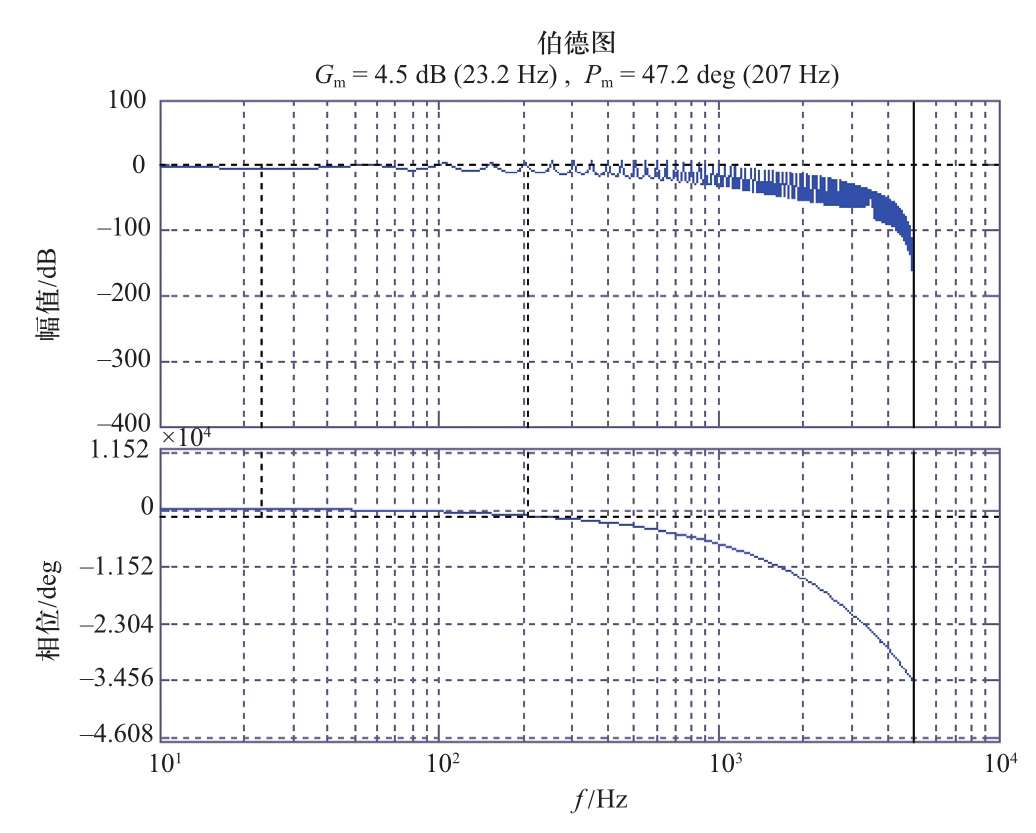
图9 等效重复控制伯德图
Fig.9 Bode diagram of equivalent repetitive control
3 仿真分析与实验验证
3.1 仿真分析
本文在Matlab/Simulink搭建了三电平逆变器仿真模型,对双PI+重复控制策略进行了验证。逆变器交流额定电压540 V,开关频率4.8 kHz。逆变器恒流模式下,电流指令800 A时并网电流波形如图10所示。
由图10可以看出,采用双PI+重复控制对并网电流的谐波有很好的抑制作用。
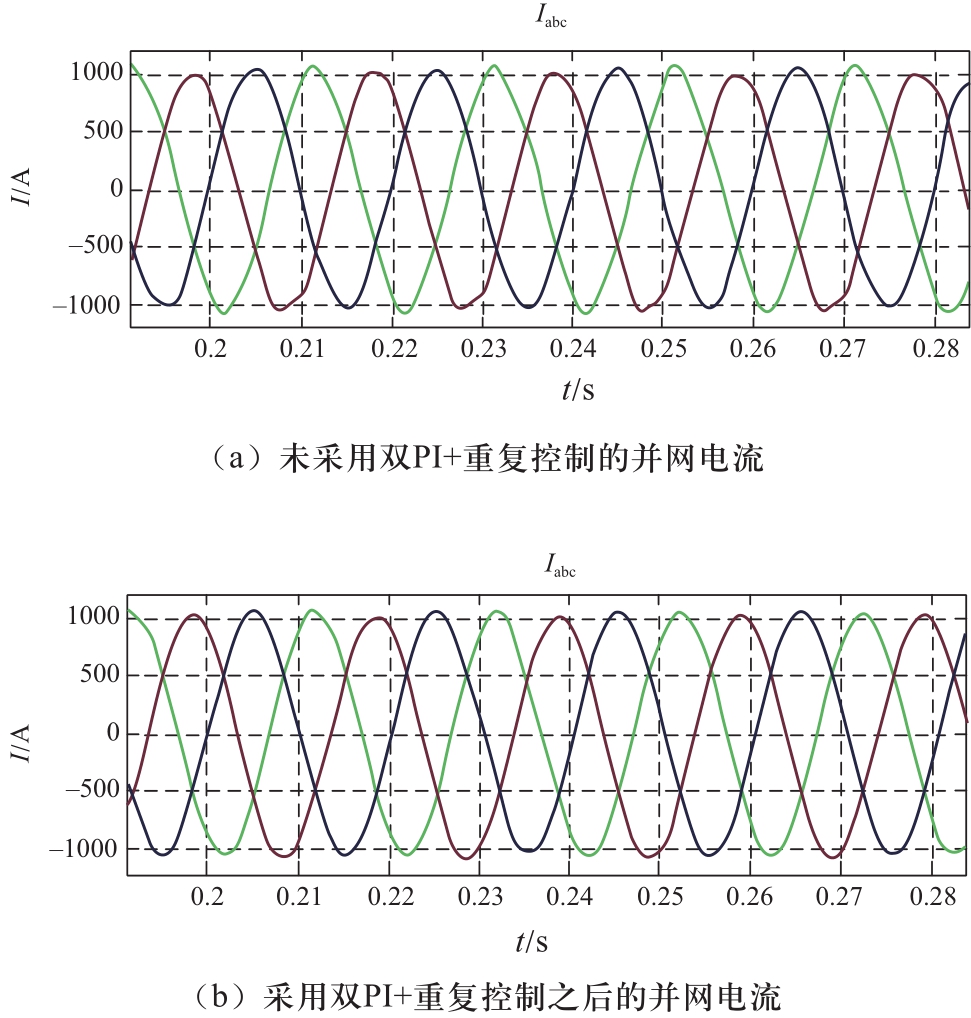
图10 采用双PI+重复控制前后并网电流对比
Fig.10 The comparison of the current diagram before and after the double PI+ repetition control was adopted
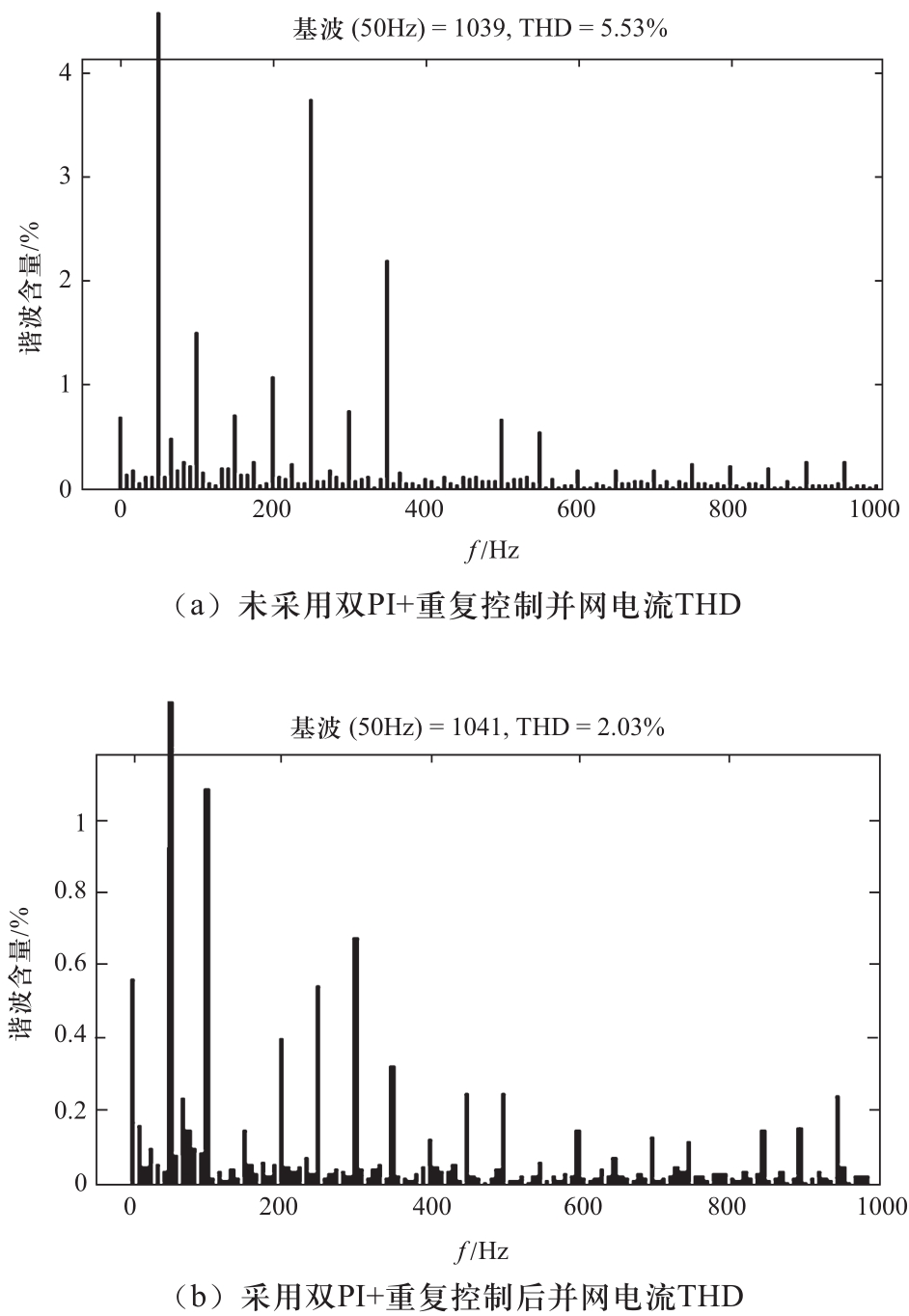
图11 采用双PI+重复控制前后并网电流THD对比
Fig.11 The comparison of the current THD diagram before and after the double PI+ repetition control was adopted
由图11仿真电流THD对比可以看出,双PI+重复控制对5次、7次、11次、13次等倍频次的谐波有明显降低。
3.2 实验验证
在现有1 MW三电平逆变器控制算法基础上融入双PI+重复控制算法,并搭建环流试验平台对算法进行验证,环流试验平台待测逆变器开关频率4.8 kHz,直流输入电压850 V,交流输出电压540 V;恒压恒流模式下对逆变器在30%额定功率点的电流波形进行测试,相同工况下,加入双PI+重复控制前后的电流波形如图12所示。

图12 采用双PI+重复控制前后逆变器并网电流对比
Fig.12 The comparison of the current diagram before and after the double PI+ repetition control was adopted
由图12实验波形对比可以看出,采用双PI+重复控制后,逆变器谐波特性变好。其中总的谐波含量由5.82%降到3.37%,5次谐波含量由4.068%降到1.98%,7次谐波含量由3.890%降到1.697%,谐波抑制效果明显。
4 结论
本文在分析三电平逆变器谐波产生原因的基础上,分析了重复控制策略对并网电流谐波抑制的机理;并分析了PI+重复控制系统的稳定性:经分析指出传统PI+重复控制等效控制对象不稳定,从而导致系统稳定性差。针对于此,本文提出了双PI+重复控制,兼顾PI+重复控制系统快速性和准确性的同时,提高了系统的稳定性,从而能够有效地对并网电流谐波进行抑制。最终通过仿真和试验,验证了双PI+重复控制对谐波抑制的可行性与有效性。该策略同样也可应用于其他电力电子并网产品中。
参考文献
[1]郭虎成. 三电平逆变器控制技术研究现状[J]. 机械制造与自动化,2013,41(1):179-180,183.Guo Hucheng. Development of Control Technology for Three-Level Inverter[J]. Machine Building & Automation,2013,41(1): 179-180, 183(in Chinese).
[2]王兆安,杨君,刘进军. 谐波抑制和无功功率补偿[M]. 北京:机械工业出版社,2016,1.
[3]费万民,吕征宇,姚文熙. 三电平逆变器特定谐波消除脉宽调制方法的研究[J]. 中国电机工程学报,2003,23(9):11-15.Fei Wanmin, Lyu Zhengyu, Yao Wenxi. Research on Selected Harmonic Elimination PWM Technique Applicable to Three-Level Voltage Inverters[J]. Proceedings of the CSEE, 2003,23(9): 11-15(in Chinese).
[4]张云,孙力,孙醒涛,等. 三相H桥三电平逆变器谐波抑制方法[J]. 电力自动化设备,2009,29(9):21-25.Zhang Yun, Sun Li, Sun Xingtao, et al. Harmonic Suppression of Three-Phase Three-Level Inverter with H Bridges[J].Electric Power Automation Equipment, 2009, 29(9): 21-25(in Chinese).
[5]孟建辉,石新春,付超,等. 基于PR控制的光伏并网电流优化控制[J]. 电力自动化设备,2014,34(2):42-47.Meng Jianhui, Shi Xinchun, Fu Chao, et al. Optimal Control of Photovoltaic Grid-Connected Current Based on PR Control[J].Electric Power Automation Equipment, 2014, 34(2): 42-47(in Chinese).
[6]梁燕,李生林,周长新,等. 组串式逆变器谐波抑制策略[J]. 自动化技术与应用,2017,36(3):67-70.Liang Yan, Li Shenglin, Zhou Changxin, et al. Harmonic Elimination Strategy of String Inverter Systen[J]. Techniques of Automation and Application, 2017, 36(3): 67-70(in Chinese).
[7]陈东,张军明,钱照明,等. 一种具有频率变化适应性的并网逆变器改进型重复控制方法[J]. 电工技术学报,2014,29(6):64-70.Chen Dong, Zhang Junming, Qian Zhaoming, et al. An Improved Repetitive Control Scheme for Grid-Connected Inverter with Frequency-Varying Adaptability [J]. Transactions of China Electronic Technical Society, 2014, 29(6): 64-70(in Chinese).
[8]Zhou Keliang, Low K, Wang D, et al. Zero-phase Odd Harmonic Repetitive Controller for a Single-phase PWM Inverter [J]. IEEE Transactions on Power Electronics, 2006,21(1): 193-201.
[9]Yang Shuitao, Cui Bin, Zhang Fan, et al. A Robust Repetitive Control Method for CVCF Inverters with Very Low Harmonic Distortion [C]//Applied Power Electronics Conference,Anaheim, CA, USA, 2007.
[10]王禹玺,刘秦维,刘伟,等. 一种加权式并联型重复控制的研究[J]. 电工技术学报,2015,30(8):127-134.Wang Yuxi, Liu Qinwei, Liu Wei, et al. Study of Weighted Parallel-Type Repetitive Control[J]. Transactions of China Electronic Technical Society, 2015, 30(8): 127-134(in Chinese).
[11]王斯然,吕征宇. LCL 型并网逆变器中重复控制方法研究[J]. 中国电机工程学报,2010,30(27):69-75.Wang Siran, Lyu Zhengyu. Research on Repetitive Control Method Applied to Grid-Connected Inverter with LCL Filter[J]. Proceedings of the CSEE, 2010, 30(27): 69-75(in Chinese).
[12]张崇巍,张兴. PWM整流器及其控制[M]. 北京:机械工业出版社,2003,10.
A Strategy for Harmonic Suppression of Photovoltaic Inverter Based on Double PI+ Repetitive Control
Liu Chong-yang, Gao Zhi-jun, Liu Gang, Sun Jian, Li Jian-wei
(Xuji Group Corporation, Xuchang 461000, Henan Province, China)
Abstract:In this paper, the main circuit structure of the photovoltaic inverter is analyzed, the mathematical model of the net output current is generated, and the mechanism of harmonic generation of inverter under this model is analyzed.Based on the analysis of traditional PI+ repetitive control,for the problem of the equivalent repetitive control object instability easily caused by the coupling of traditional PI and repetitive control, this paper presents a control strategy of Double Proportional Integral + Repetitive Control (DPI+RC).By using PI compensation, the stability of the system is ensured by ensuring the speed and accuracy of traditional PI+ repetitive control system tracking. Finally, the feasibility of the control strategy for harmonic suppression is verified through simulation and experimental analysis.
Keywords:photovoltaic inverter; PI compensation; double PI +repetitive control; harmonic suppression

刘重洋
作者简介:
刘重洋(1988),男,硕士研究生,研究方向为电力电子应用、新能源控制。E-mail:liuchongyang_xj@foxmail.com。
高志军(1985),男,硕士研究生,研究方向为大功率电力电子设备并网技术。
刘刚(1973),男,硕士研究生,高级工程师,研究方向为大功率电力电子变流技术与应用。
(责任编辑 赵杨)
