0 引言
配电网处于电力系统的末端,直接面向电力用户。当前,配电网存在网架结构薄弱、自动化水平低等问题;同时,光伏、风电等新型电源,以及电动汽车等新型负荷的接入,使得配电网内电压波动越限、馈线功率失衡等现象日趋严重[1-2]。常规配电网调控手段无法有效解决以上问题。
智能软开关(soft normally open point,SNOP)就是在上述背景下衍生出的安装于传统联络开关处的电力电子装置,它能够准确控制其所连接馈线的有功功率与无功功率,从而有效应对分布式电源和负荷带来的随机性和波动性[3-4]。SNOP的引入彻底改变了传统配电网闭环设计、开环运行的供电方式,避免了开关变位造成的安全隐患,大大提高了配电网控制的实时性与快速性,同时给配电网的运行带来了诸多益处[5]。
基于模块化多电平换流器(modular multilevel converter,MMC)的背靠背型两端/多端柔性直流配电系统是SNOP其中一种实现形式。MMC采用子模块级联实现多电平输出,无需器件直接串联,具有损耗低、可靠性高等优点,在国内外得到了广泛应用[6-7]。MMC通常采用联接变压器与交流系统相连。联接变压器可以实现交直流系统的故障隔离,提高系统运行的可靠性。但是,联接变压器的配置使得柔性直流配电系统的成本和占地大幅度增加。SNOP离城市负荷中心较近,对紧凑化设计的要求较高,因此,SNOP需要考虑无联接变压器的设计方案[8-10]。
SNOP在无变压器的情况下,交流系统的零序分量将不能被天然隔离,一个交流系统的零序分量将通过SNOP传递至其他相连的交流系统,扩大系统影响范围。文献[8]提出了双换流变、单换流变和无换流变三种柔性环网控制器拓扑结构,结合交直流故障特性分析,综合比较了三者优缺点。文献[9]根据柔性环网控制器的技术特点提出了平波电抗器、联接变压器等设备的紧凑化方法,以减小设备占地面积及投资,适应不同场合需求。文献[10]针对分区互联装置单变压器的拓扑结构,分析了桥臂闪络故障的故障特性,提出了基于闭合子模块旁路开关的保护动作策略,确保交流断路器可靠动作。文献[11]研究了单变压器分区互联装置交流系统单相接地故障和直流系统单极接地故障的相关特性,分别提出了零序电压策略和基于切除子模块和闭合子模块旁路开关的保护动作策略。文献[12]分析了无变压器柔性环网控制装置的交、直流故障特性,推导了故障后换流器在不同工作模式下故障电流的解析方程。然而,现有研究缺少对无变压器情况下交流系统发生不对称接地故障时,SNOP系统本质特性的分析和理论推导,以及相应控制策略设计。
SNOP通常连接于馈线末端,本文以接入交流10 kV配电系统的±10 kV基于无变压器MMC型的SNOP为研究对象,结合10 kV配网中性点经消弧线圈接地的系统特征,通过理论推导的方式,揭示零序分量在交直流之间的传递特性,然后,从抑制零序分量的角度出发,提出有效的系统拓扑及相应控制策略,满足无变压器型SNOP交流故障穿越要求,提高系统运行可靠性。
1 系统接线及数学模型
SNOP具有多种系统接线形式,图1给出三种典型方式。SNOP1:连接同一个10 kV供区内的两条不同馈线;SNOP2:连接两个不同10 kV供区的两条馈线;SNOP3:连接三(多)个不同供区的三(多)条馈线。三个供区都采用中性点经消弧线圈接地方式,MMC与交流供区直接相连,共用接地支路。下文以SNOP2为例进行研究。
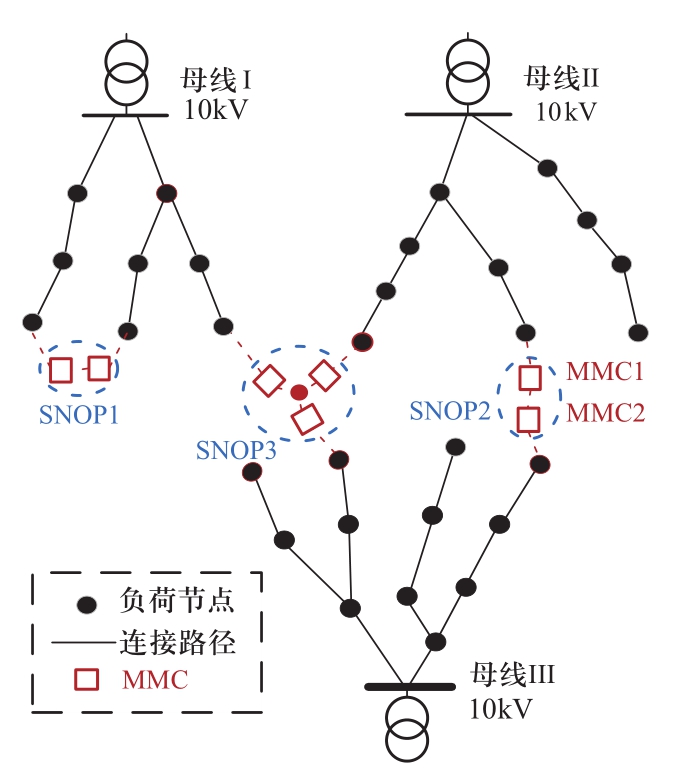
图1 SNOP系统接线形式
Fig.1 System connection form of SNOP
图2 给出了MMC的结构示意图。桥臂电感的电感值记为2L,桥臂等值电阻记为2R。外部交流系统的三相输入电压分别用ua、ub和uc来表示,外部交流系统的三相输入电流分别用ia、ib和ic来表示。直流侧输出电压和输出电流分别用 Ud和 Id来表示,正极直流电压和负极直流电压分别用 Udp和 Udn表示,“o”点表示直流侧的虚拟中性点。j相(j=a, b,c)上桥臂和下桥臂电流分别用 ijp和ijn来表示,ujp和ujn分别是j相上桥臂和下桥臂串联子模块组的输出端电压,uo是直流侧中性点的对地电压。半桥子模块(half-bridge submodule, HBSM)的结构如图2(c)所示。
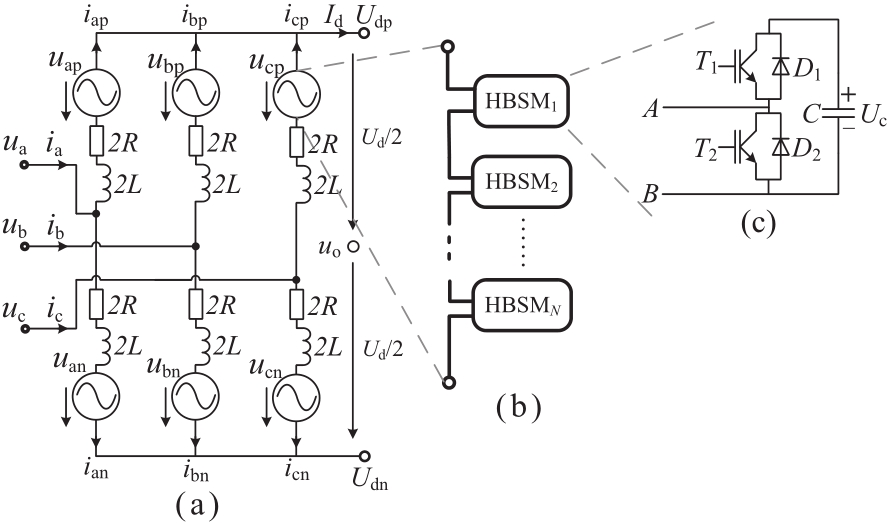
图2 MMC结构示意图
Fig.2 Schematic diagram of MMC
根据文献[13]的公式推导结果,有
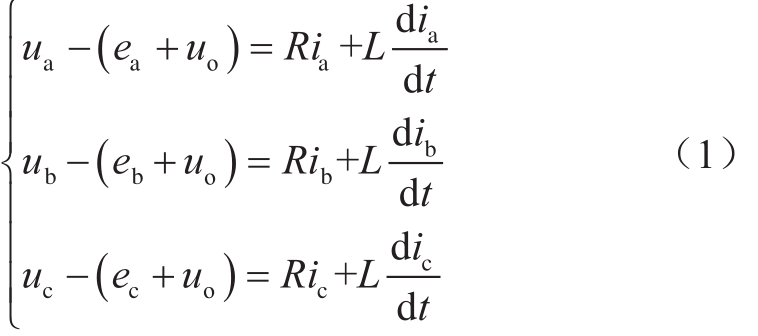
其中,![]()
根据对称分量法及式(1),MMC的交流侧动态数学模型可以分解为正序分量、负序分量和零序分量三个独立的子系统。
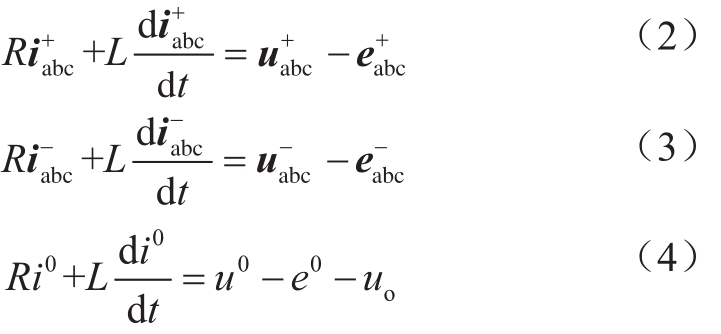
从式(2)和(3)可以看出,正负序分量内,已无 uo项,表明 uo与正负序系统无关,仅由零序系统决定。正序分量和负序分量经正、负序 dq 变换,并经拉普拉斯变换后的数学模型已十分成熟[13],在此不再赘述。
根据式(4)零序公式,可以得到图3所示的MMC零序数学模型。
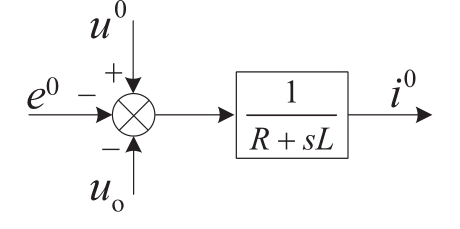
图3 MMC零序数学模型
Fig.3 Zero-sequence mathematical model of MMC
2 传统正负序控制下的故障响应特性
为实现交流故障穿越,根据正负序数学模型所建立的正负序系统下的内外环控制策略也已十分成熟[14],在此不再赘述。无论是控制正负序下的功率还是电流,控制环节生成的最终指令都是通过调节图2所示的 ujp和 ujn实现。而仅考虑正序分量和负序分量控制的控制器,实际输出的 ujp和 ujn必然仅包含正序分量和负序分量,ej也只包含有正负序分量,而无零序分量,即e0= 0。
因此,在传统仅具有正负序分量控制的策略下,不对称故障时,式(4)可改写为
采用中性点经消弧线圈接地的10 kV配电系统在发生对称接地或不对称接地故障时,接地电流往往较小,继而i0≈ 0。因此,从式(5)可得
由于正负极直流电压Udp和Udn分别为0.5Ud+ uo和uo—0.5Ud,交流系统发生不对称接地故障时,uo将为非零量,会导致正负极直流电压的偏移波动,但直流极间电压保持不变。
由于图1所示的MMC1和MMC2采用背靠背连接形式,“o”点可视为两者直流侧的公共虚拟中性点。在MMC1交流侧发生不对称接地故障导致“o”点电压偏移时,MMC2由于均只配置有正负序控制器,通过公式(5)反推可知,MMC2的交流侧将因“o”点电压的偏移导致出现零序电压分量,且该零序分量的大小与MMC1侧近乎相同(忽略回路上部分零序阻抗压降)。零序分量的引入,将导致MMC2交流电压的波动。如此,相当于将MMC1侧的不对称接地故障传递至了MMC2所在的供区,引起故障扩大化。
在10 kV经消弧线圈接地的配电系统中,单相接地故障下,配电系统允许暂时运行2小时,以提高供电可靠性。此种情况下,SNOP若不闭锁,与MMC1和MMC2相连的两个供区相当于共同经历了2小时接地故障,整个配电系统的安全稳定运行会受到较大的冲击。
3 单相接地故障特性分析
根据上述分析,为进一步定量分析系统不对称故障特性,以图1中与MMC1相连的交流馈线发生C相金属性接地故障为例进行相应故障特性分析。若故障前,三相电压对称,额定相电压幅值为Um,A相初始相位为φ1。接地故障发生后,故障相对地电压为0,非接地相对地电压幅值升为线电压[12]。
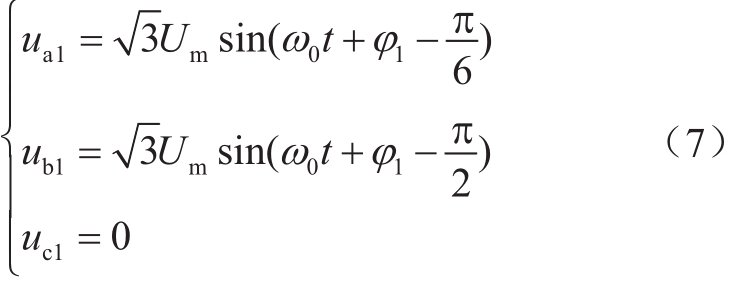
采用对称分量法可得正序、负序、零序电压为

C相发生单相金属性接地故障时,正序分量和零序分量幅值相同,均为额定相电压幅值。从式(6)可得
令电压调制比k(k < 1)为
那么,正极直流电压Udp和负极直流电压Udn分别为
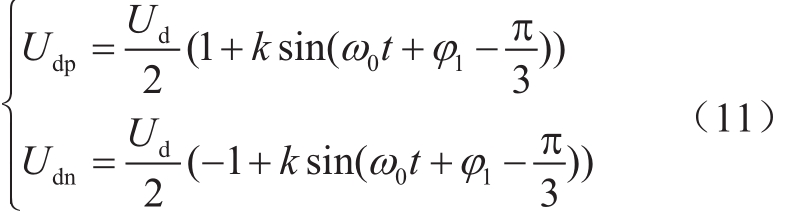
从式(11)可以看出,正负极直流电压发生工频波动,波动幅值等同于交流相电压幅值Um。正极和负极虽有电压波动,但波动仍维持在正负极的极性范围之内,未发生极性反转情况。正极直流电压的最大值为0.5(1+k)Ud,最小值0.5(1-k)Ud;负极直流电压的最大值为-0.5(1+k)Ud,最小值为-0.5(1-k)Ud。可见正极和负极的最大电压已接近极间电压,对系统的安全运行造成影响。
对于MMC2而言,由于uo存在式(9)的电压波动,由式(5)和(6)可知,MMC2的交流系统中,将会引入同式(9)的零序电压。MMC2交流系统未发生接地故障,因而MMC1交流侧单相接地故障发生前,MMC2交流系统仅含有正序分量,即(为简化问题分析,假设MMC2交流侧的稳态相电压幅值与MMC1相同,两者具有相同的电压调制比):
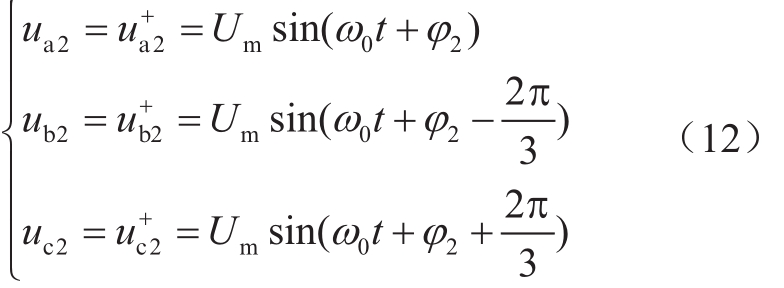
其中,φ2为初始相位。采用对称分量法的逆变换计算(a = ej120°),可以确切得出MMC2交流系统在MMC1交流侧故障时的电压如式(13)所示。利用式(13)即可定量获得MMC2的交流电压特性。
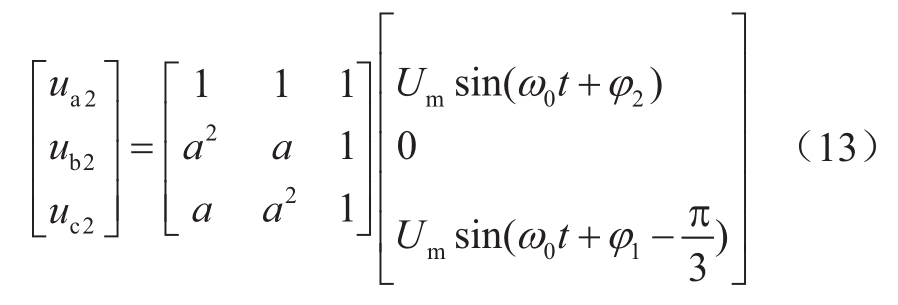
(1)若φ1-φ2=0,即MMC1交流系统与MMC2交流系统的相位相等或十分相近,有
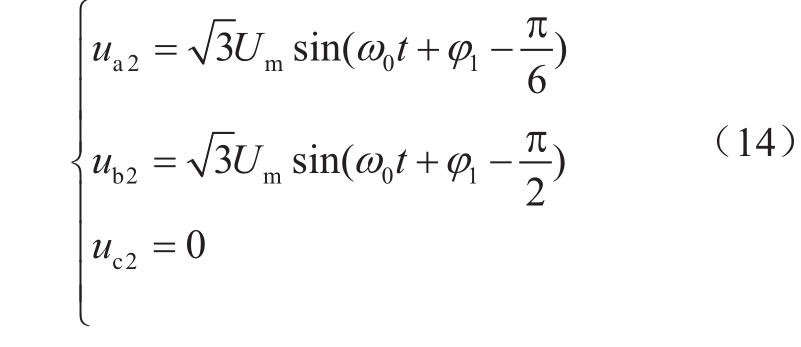
对比式(7)和(14)可知,在忽略一些阻抗压降的情况下,MMC2的交流电压与MMC1(故障侧)的近乎相同。相当于MMC2交流侧C相发生金属性接地故障。
(2)若φ1-φ2≠0,则MMC2的交流电压将随相角差的变化而变化。在一个城市配网内,SNOP所连供区之间的相角差一般不会较大,比如在-15°~15°之间,因此,MMC2具体的电压值虽然与式(14)不同,但仍较为接近,式(14)仍具有参考价值。
需要指出的是,本节只是以单相金属性接地故障为例进行了理论计算和推导,若为两相故障或单相经电阻接地故障,亦可采用类似的方法进行理论计算,以定量了解不对称故障对两个供区电压特性的影响。
4 对应优化策略
4.1 控制策略优化
从上述理论推导可以看出,直流电压的工频波动是由“o”点电压uo非零所致。为抑制零序分量通过SNOP从一侧传递至其他侧,减小故障影响范围,就需要通过相应控制策略,将uo限制于零值附近。从式(4)和图3可以看出,唯有将e0控制于
才能有效达到直流电压波动抑制的目的。另一方面,零序电流会流过桥臂,引发电力电子器件过热等问题,尤其是零序电流较大的情况下,因此,还需要增加对零序电流的控制。
零序电流以工频交流量的形式存在,基于现有已熟知的比例谐振(proportional resonant,PR)控制器[15-16]可以实现交流信号无差调节的常识,根据式(15)内各变量之间的数学关系,本文针对性地设计了如图4所示的零序控制环节。其中,Kp为比例系数;KR为谐振系数;ω0为控制交流信号的角频率;ωc为截止频率。为消除零序电流分量,PR控制器输入端的零序电流参考值设置为0,同时,为抑制零序电压引起“o”点电压波动,引入交流电压零序分量u0作为前馈量。
4.2 拓扑结构要求
加入零序控制环节后,桥臂电压将引入零序分量,桥臂内正、负、零序电压的矢量叠加即是桥臂电压真正的输出要求。如此,便需要考虑如下问题:每个桥臂能够输出的电压由子模块结构、子模块电容电压和子模块个数共同决定,其输出电压范围有限,当零序电压引入后,现有的MMC桥臂能否输出满足要求的电压值。
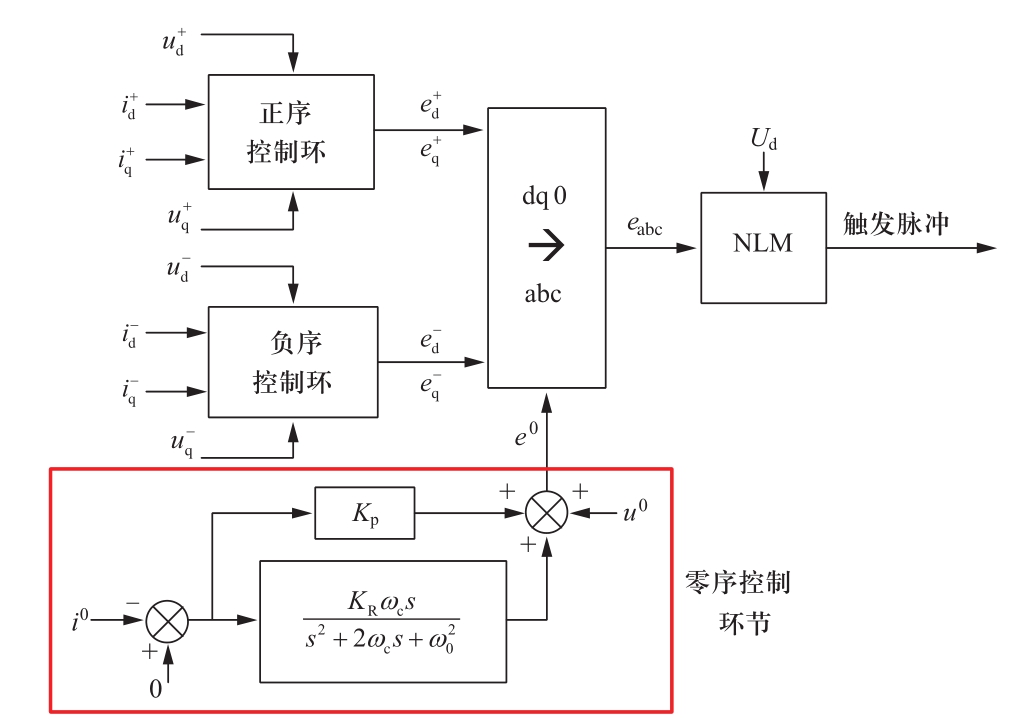
图4 MMC优化控制策略
Fig.4 Optimized control strategy of MMC
实际上,当正、负、零序电流被有效限制在允许范围内时,桥臂电感、电阻等压降由于幅值太小基本可以不考虑,因此,换流器出口处的交流电压与uj近似相同。每个桥臂输出的电压如下式所示:

不同故障下,uj各相电压幅值均不同。以单相接地故障为例,将式(7)代入上式,可知A相和B相桥臂所需输出的最大电压和最小电压为式(17)和(18),C相桥臂输出的电压几乎恒为0.5Ud。
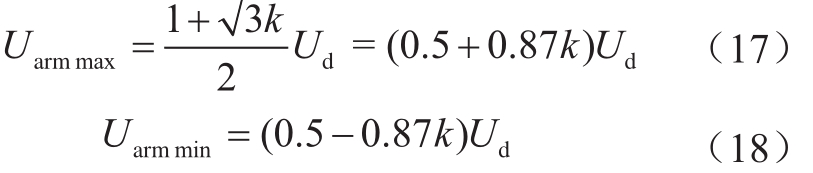
若要求SNOP能够完全控制各序分量,则每个桥臂需含有能够输出负电平的(0.87k - 0.5)N个子模块,同时,能够输出正电平的子模块个数应达到(0.87k + 0.5)N,其中,N=Ud/ Uc,Uc为子模块电容电压。稳定运行时,电压调制比 k 一般介于0.8~0.95。若取 k = 0.85,则负电平个数为0.24N,正电平个数为1.24N。
4.3 混合型MMC
根据上述分析可知,由于HBSM仅具备正、零两种电平输出能力,因此,纯粹的半桥MMC不能满足上述要求,需采用具有负电平输出能力的子模块。当前,具备负电平输出能力的子模块拓扑结构形式已较多,本文以全桥子模块(full-bridge sub-module,FBSM)为例进行阐述。单个FBSM具有正、零、负三种电平输出能力,为满足零序抑制的目的同时又节省投资成本,可采用HBSM和FBSM混合级联而成的混合型MMC结构形式。根据上节的分析结果可知,在不考虑子模块冗余的情况下,单个桥臂所需的FBSM个数为(0.87k—0.5)N,HBSM个数为N。
中性点经消弧线圈接地的10 kV系统中,一般单相接地故障所导致的相电压抬升最为严重。因此,按照上述方法构成的混合型MMC能够满足其他故障类型下系统零序分量的抑制要求,平抑直流电压波动以及零序分量向非故障供区的传递。
为降低子模块增加和替换所需的投资成本,从式(16)可以看出,通过降低交流故障期间的直流电压能够达到子模块增加个数减少的目的,本文受限于篇幅,不再展开说明。无论是降直流电压还是不降直流电压,图4所示的控制策略均适用。
5 仿真分析
5.1 仿真参数
在电磁暂态仿真软件PSCAD/EMTDC中搭建了如图5所示的仿真平台。额定直流电压为±10 kV,每个MMC额定功率为10 MW。两个10 kV供区内每条馈线以及与SNOP相连馈线上的负荷采用 Fixed Load 静态负荷模型依据不同负荷的特性进行等效建模。供区1和供区 2 均采用中性点经消弧线圈接地方式,中性点接地电感为0.78 H。分别向供区1和供区 2 供电的110 kV电网系统均采用短路比SCR=5的等效系统,且电压相角差为0。每个MMC桥臂都含有24个HBSM(包含2个冗余),HBSM的额定电压为0.91 kV,电容值为5000 μF,桥臂电抗为3 mH。
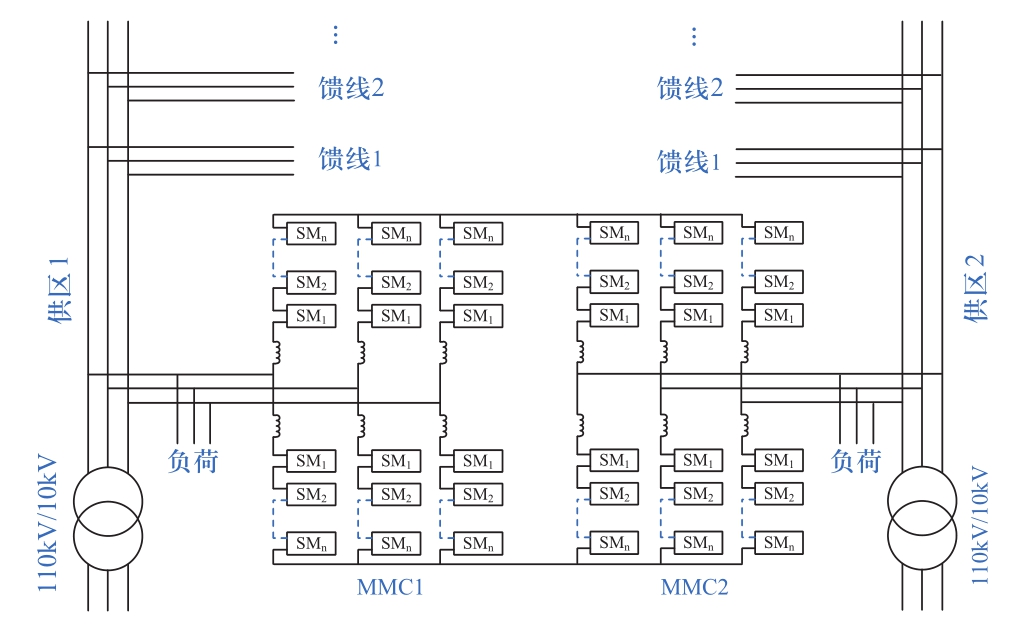
图5 仿真模型示意图
Fig.5 Schematic diagram of simulation model
5.2 传统控制策略系统响应特性
稳态运行情况下,MMC1采用定有功功率和定无功功率控制策略,MMC2采用定直流电压和定无功功率控制策略。以0.8 s~0.9 s时间段内,MMC1交流系统发生A相金属性接地故障为例。
图6(a)~(f)给出了MMC1侧三相交流电压、正负极直流电压、交流零序电压、交流零序电流、子模块电容电压和A相上桥臂子模块投入个数的响应曲线。从图中可以看出,故障发生后,A相电压突变为0,B相和C相电压升高为相电压的1.73倍,交流零序电压幅值与额定相电压幅值相同,正极直流电压和负极直流电压内,包含有与交流电压零序分量幅值和相位均相一致的工频波动,论证了式(9)的正确性。由于交流配电系统经消弧线圈接地,因此,零序电流较小,如图6(d)所示,零序电流幅值小于16 A。在整个故障期间,由于控制系统只包含正序和负序控制,而零序分量未产生实际功率,因此,MMC1桥臂子模块投切和子模块电容电压在故障期间并未发生改变。
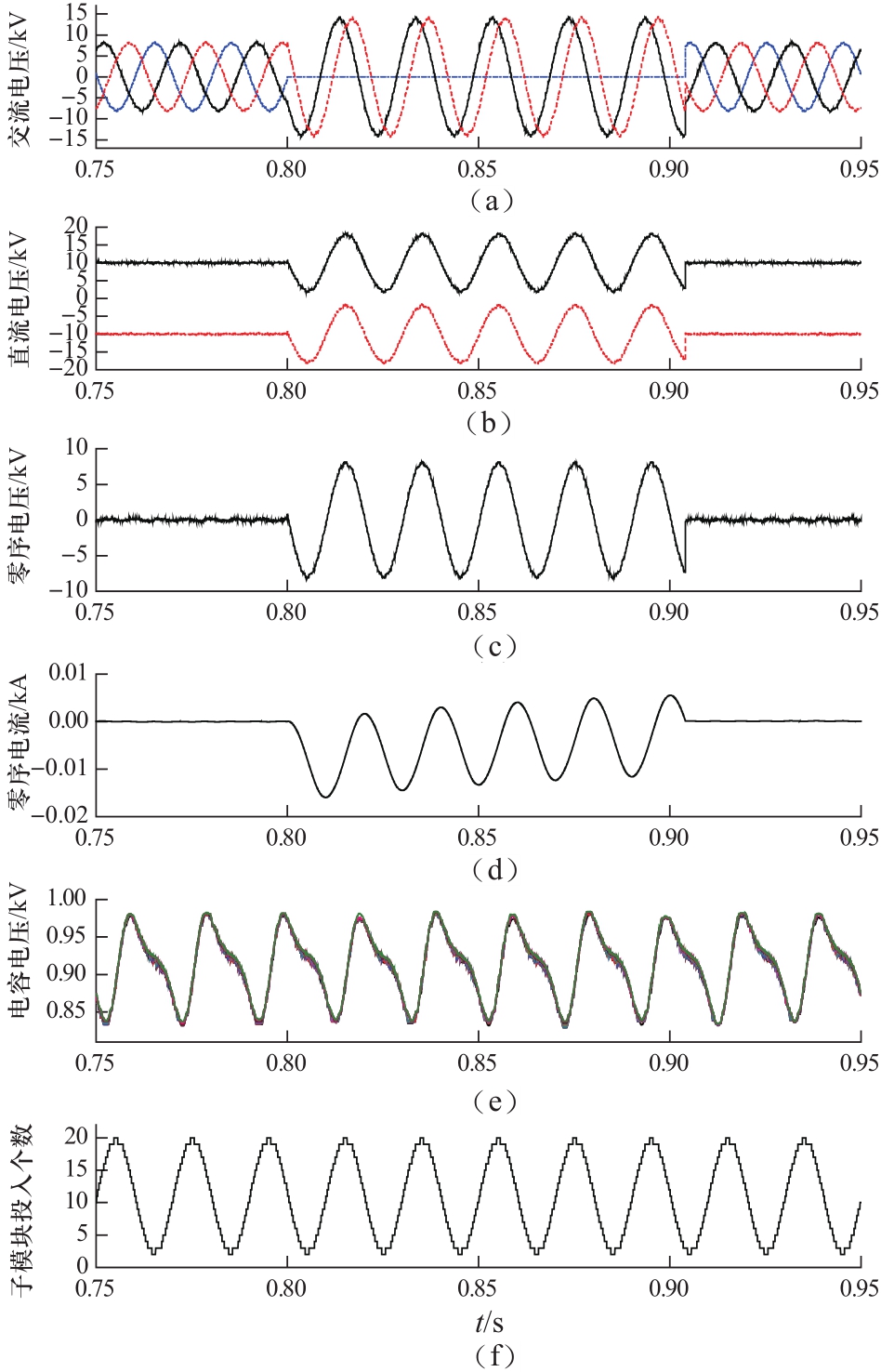
图6 优化前的MMC1故障响应特性
Fig.6 Fault response characteristics of MMC1 before optimization
图7(a)~(e)给出了MMC2侧三相交流电压、交流零序电压、交流零序电流、子模块电容电压和A相上桥臂子模块投入个数的响应曲线。从图中可以看出,故障发生后,A相电压幅值变为1.5 kV,B相和C相电压幅值升高为13.2 kV和14.8 kV,电压特性与MMC1交流侧类同,论证了上文理论推导的正确性。MMC2交流零序电压幅值与MMC1的交流零序电压相一致,零序电流较小,幅值小于16 A。在整个故障期间,MMC2桥臂子模块投切和子模块电容电压均未发生改变,原理同MMC1。
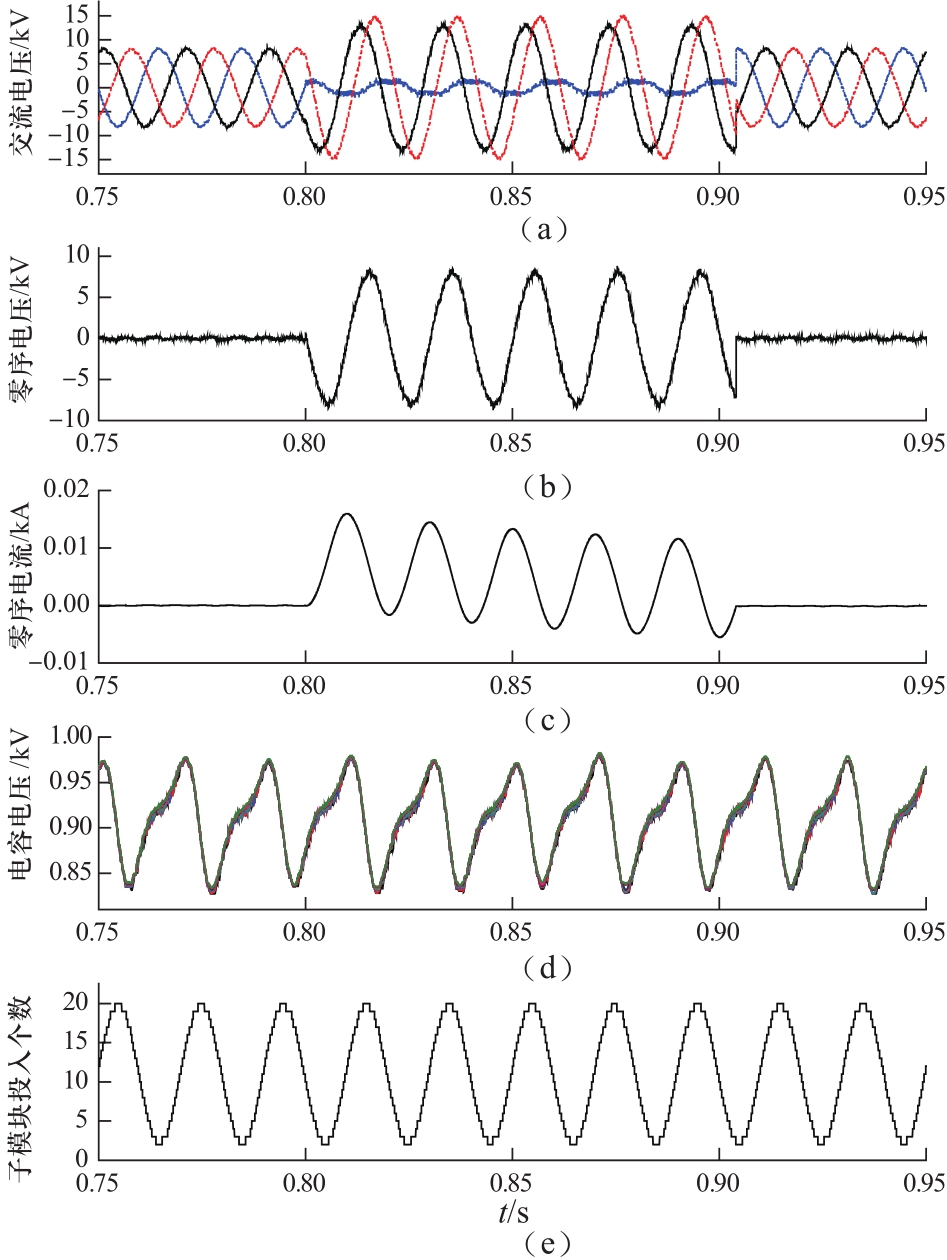
图7 优化前的MMC2故障响应特性
Fig.7 Fault response characteristics of MMC2 before optimization
5.3 优化后的系统响应特性
稳态运行下,交流配电网额定线电压为10 kV,SNOP直流侧的正负极电压为±10 kV,因此,电压调制比为0.82,根据上一节结果可得,改进后的混合型MMC内每个桥臂含有22个HBSM和5个FBSM,子模块电容值相同。t=0.8 s时刻,MMC1交流系统发生A相金属性接地故障,在t=0.9 s时刻,投入零序附加控制环。图8给出了MMC1侧三相交流电压、正负极直流电压、交流零序电流、子模块电容电压和三相上桥臂电平投入个数的响应曲线。
从图中可以看出,零序附加控制投入后,正负极直流电压波动被马上抑制,稳定运行于额定电压水平。零序电流被平抑至零值附近,子模块电容电压稳定于额定值附近,A相投入的电平数维持在11附近,B相和C相投入的电平数最大为27,最小为-5。
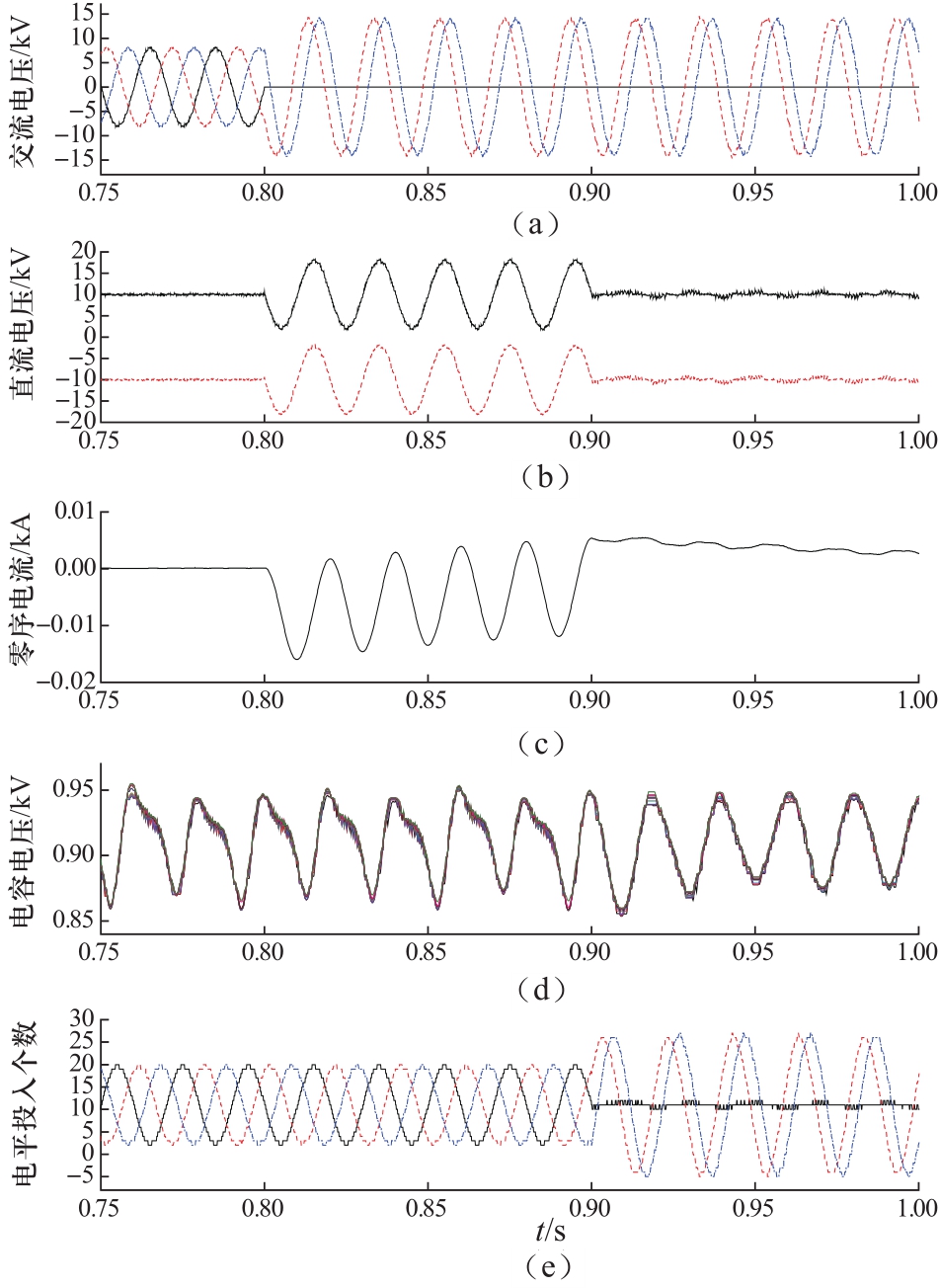
图8 优化后的MMC1故障响应特性
Fig.8 Fault response characteristics of MMC1 after optimization
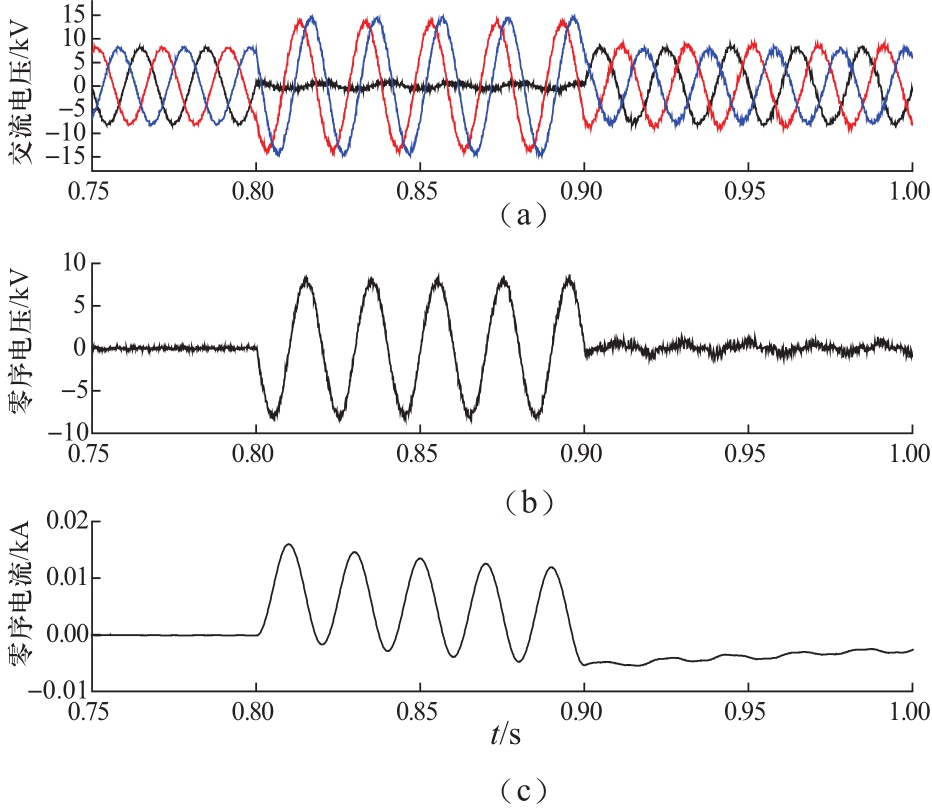
图9 优化后的MMC2故障响应特性
Fig.9 Fault response characteristics of MMC2 after optimization
图9 给出了MMC2侧三相交流电压、交流零序电压、交流零序电流的响应曲线。从图中可以看出,零序附加控制投入后,零序电压分量和零序电流分量被有效抑制,MMC2所在供区的交流电压迅速恢复至三相对称稳定状态,表明MMC1侧供区发生的故障不再影响MMC2所在供区,故障范围被有效限制。
6 结语
本文通过理论分析和公式推导揭示了SNOP在不安装联接变压器情况下,交流故障侧零序电压引发直流电压和非故障侧交流电压波动的内在机理,提出了相应策略以抑制零序分量在交直流之间的传递,并得出以下结论。
(1)当发生单相接地等不对称故障引发交流系统产生零序电压后,该零序分量会直接叠加于正负极直流电压上,引起正负极直流电压工频波动,但极间电压维持不变。同时,该零序分量通过SNOP传递至非故障供区,引发非故障系统的交流电压波动,非故障供区的电压特性与系统参数以及供区间的电压幅值和相位差相关。
(2)本文根据公式推导,提出了基于PR控制器的零序控制环和增加FBSM的混合型MMC拓扑改进方案。针对本文所描述问题的特殊性,对零序控制环和混合型MMC都进行了针对性设计。仿真结果证实了所提方法能够有效抑制供区内交流不对称故障所引发的直流电压波动和正常供区交流电压波动现象,能够将故障影响区域限制在一定范围内,有效提升配网供电可靠性。
参考文献
[1]朱正,廖清芬,刘涤尘,等. 考虑新能源与电动汽车接入下的主动配电网重构策略[J]. 电力系统自动化,2015,39(14):82-88.Zhu Zheng, Liao Qingfen, Liu Dichen, et al. Strategy of Distribution Network Reconfiguration Considering Wind Power and Electric Vehicle Integration[J]. Automation of Electric Power Systems, 2015, 39(14): 82-88(in Chinese).
[2]丁明,石雪梅. 新能源接入对主动配电网的影响[J]. 电力建设,2015,36(1):76-84.Ding Ming, Shi Xuemei. Effect of New Energy Paralleling to the Active Distributed Networks[J]. Electric Power Construction, 2015, 36(1): 76-84(in Chinese).
[3]王成山,孙充勃,李鹏,等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化,2015,39(9):82-87.Wang Chengshan, Sun Chongbo, Li Peng, et al. SNOP-based Operation Optimization and Analysis of Distribution Networks[J]. Automation of Electric Power Systems, 2015,39(9): 82-87(in Chinese).
[4]王岸. SNOP的研究及其在配电网中的应用[D]. 北京交通大学,2015.
[5]李智诚,吴建中,和敬涵,等. 软常开点的双闭环控制及其在配电网中的应用[J]. 智能电网,2013,1(1):49-55.Li Zhicheng, Wu Jianzhong, He Jinghan, et al. Dual Closed-Loop Control of Soft Normally OpenPoints and Its Application in Distribution Networks[J]. Smart Grid, 2013, 1(1): 49-55(in Chinese).
[6]许烽,徐政,张哲任,等. 基于降损调制技术的全桥MMC电容电压无需排序均衡控制[J]. 电网技术,2013,37(12):3347-3355.Xu Feng,Xu Zheng,Zhang Zheren, et al. Reduced Loss Modulation Based Capacitor Voltage Non-sorting Balancing Control for Full-bridge MMC[J]. Power Systems Technology,2013, 37(12): 3347-3355(in Chinese).
[7]熊桥坡,罗安,马伏军. 模块化多电平SVG负序补偿容量比较[J]. 中国电机工程学报,2014,34(24):4049-4056.Xiong Qiaopo,Luo An,Ma Fujun. Comparison of Negative Sequence Compensation Capacity Between SVGs based on Modular Multilevel Converters[J]. Proceedings of the CSEE,2014,34(24):4049-4056(in Chinese).
[8]高凯,阳岳希,张艳军,等. 适用于城市电网的柔性环网控制器拓扑方案研究[J]. 电网技术,2016,40(1):78-85.Gao Kai, Yang Yuexi, Zhang Yanjun, et al. A Topology Research of Flexible Looped Network Controller Suitable to Urban Power Grid[J]. Power System Technology, 2016, 40(1):78-85(in Chinese).
[9]张艳军,周季,高凯,等. 柔性环网控制器原理及紧凑化研究[J]. 智能电网,2017,5(5):434-441.Zhang Yanjun, Zhou Ji, Gao Kai, et al. Research on the Principle and Compact of Flexible Looped Network Controller[J]. Smart Grid, 2017, 5(5): 434-441(in Chinese).
[10]尹昌新,李蕴,陈平,等. 分区互联装置桥臂闪络故障保护策略设计[J]. 电力建设,2017,38(2):100-105.Yin Changxin, Li Yun, Chen Ping, et al. Protection Scheme Design for Interconnecting Device Under Arm Flashover Fault[J]. Electric Power Construction, 2017, 38(2): 100-105(in Chinese).
[11]周杨,尹昌新,贺之渊,等. 单变压器分区互联装置接地故障特性研究及控制保护策略设计[J]. 中国电机工程学报,2017,37(23):6901-6909.Zhou Yang, Yin Changxin, He Zhiyuan, et al. Characteristic Investigation and Control of Single Transformer Interconnecting Device Under Grounding Fault Condition[J].Proceedings of the CSEE, 2017, 37(23): 6901-6909(in Chinese).
[12]姜田贵,谢晔源,李洪涛,等. 中性点经消弧线圈接地系统中柔性环网控制装置接地故障分析[J]. 电力建设,2016,37(5):146-152.Jiang Tiangui, Xie Yeyuan, Li Hongtao, et al. Grounding Fault Analysis of Flexible Loop Network Control Device in Neutral Point Grounding System with Arc Suppression Coil[J]. Electric Power Construction, 2016, 37(5): 146-152(in Chinese).
[13]管敏渊. 基于模块化多电平换流器的直流输电系统控制策略研究[D]. 浙江大学,2013.
[14]徐政,屠卿瑞,管敏渊,等. 柔性直流输电系统[M]. 北京:机械工业出版社,2013.
[15]胡家兵,贺益康,王宏胜,等. 不平衡电网电压下双馈感应发电机转子侧变换器的比例-谐振电流控制策略[J]. 中国电机工程学报,2010,30(6):48-56.Hu Jiabing, He Yikang, Wang Hongsheng, et al. Proportionalresonant Current Control Scheme for Rotor- side Converter of Doubly-fed Induction Generators Under Unbalanced Network Voltage Conditions[J]. Proceedings of the CSEE, 2010, 30(6):48-56(in Chinese).
[16]曾恒力,年珩,周义杰. 基于比例谐振控制的共直流母线开绕组永磁同步电机零序电流抑制技术[J]. 电工技术学报,2016,31(22):35-44.Zeng Hengli, Nian Heng, Zhou Yijie. Zero Sequence Current Suppression for Open Winding Permanent Magnet Synchronous Motor with Common DC Bus Based on Proportional-resonant Controller[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 35-44(in Chinese).
Fault Characteristics and Corresponding Strategies of Transformerless Soft Normally Open Point
XU Feng1,2, XUAN Xiao-hua1, YU Hai-hong1, LU Yi1, QIU Peng1, JIANG Dao-zhuo2, HUANG Xiao-ming3
(1. State Grid Zhejiang Electric Power Research Institute, Hangzhou 310014, Zhejiang Province, China;2. College of Electric Engineering, Zhejiang University, Hangzhou 310027, Zhejiang Province, China;3. Huzhou Power Supply Company of State Grid Zhejiang Electric Power Company, Huzhou 313000, Zhejiang Province, China)
Abstract:This paper focuses on the soft normally open point(SNOP) which has no transformers and connects to the 10 kV distribution network through the arc suppression coil grounding mode. A mathematical model of positive, negative and zero sequence components under AC fault is established, by the circuit analysis and the sequence component decomposition.Then the mechanism of the voltage fluctuation at the DC side and non-fault AC fault caused by the zero-sequence voltage at the fault side is analyzed under the case without transformers.Taking the single-phase grounding fault as an example, the fluctuation formula of the DC voltage and AC voltage is deduced in detail. Based on the theoretical analysis, the zerosequence control strategy and the sub-module improvement strategy of the modular multilevel converter (MMC) are proposed. A back-to-back SNOP simulation model is established in PSCAD/EMTDC. The simulation results verify the accuracy of the theoretical analysis under AC faults, and the validity of zero-sequence control and MMC topology improvement strategies.
Keywords:no transformer; SNOP; MMC; zero-sequence component; FBSM

许烽
作者简介:
许烽(1988),男,博士,工程师,主要研究方向为高压直流输电和柔性直流输电及大功率电力电子技术。E-mail:xuf_1988@163.com。
宣晓华(1965),男,硕士,教授级高级工程师,主要研究方向为电力系统继电保护和计算机自动化。
虞海泓(1971),男,学士,高级工程师,主要研究方向为电力系统规划和设计。
(责任编辑 张鹏)
