0 引言
电化学储能技术因可灵活、高效地改善随机性、间歇性新能源的可调控性能,被认为是推动风、光等可再生能源成为主力电源的关键技术之一。但是现阶段大规模储能技术由于投资成本高,缺少固定收益模式,因此商业化程度较低。与此同时,电动汽车作为保障能源安全和低碳转型的重要技术途径,近年来得到了井喷式的发展。
按美国电动汽车协会推荐的标准,为保证续驶里程和安全运行,汽车电池在剩余80%标称容量时应退役更换[1-2]。随着电动汽车保有量的增加,未来动力锂离子电池退役量逐年增加,有研究机构预测,2019年将迎来退役电池的吉瓦时时代,2025年预计动力锂离子电池退役量将接近100 GWh。大批量动力电池不断退役,为电力储能的低成本化带来机遇,有望最大化发挥电池全寿命周期价值。
2002年至2010年,国际上对电动汽车电池的退役再利用技术进行了充分的研究,自2010年,研究机构开始探索动力电池退役后在储能系统中应用的可能性,并进行实证试验,2014年包括宝马、丰田等各个电动汽车生产企业开始全面布局梯次利用市场,建设梯次利用电池储能系统。中国自2011年开始研究电池梯次利用的筛选原则、成组方法和系统方案,并在充换电站和混合微电网中进行应用。梯次利用电池储能系统从理论研究到小规模示范电站出现,并随着技术进步规模逐渐扩大。
与新电池相比,退役电池存在性能离散度高、容量跳水可能性增大等特征,导致梯次利用储能系统可用容量下降、安全失效风险加剧,因此在使用退役电池前,需要对其性能进行评估,推测该电池的后续应用性能。本文主要研究通过抽检试验,推测退役电池后续容量衰退路径,即构建寿命预测模型。现阶段依据机理、特征和历史数据可将退役动力电池的寿命预测方法分为三种。基于机理的寿命预测方法[3],首先对电池的物理化学过程进行模型描述,然后研究老化过程对状态变量影响的规律,但这种预测模型需要精细的参数,复杂程度较高,针对老化因素的测试比较复杂[4-6]。基于特征分析的寿命预测是利用电池老化过程中所表现出来特征参量的演变,建立特征量提取值与电池健康状态之间的对应关系用于寿命预测[7-9]。主要是分析电化学阻抗谱与寿命的关系,但在工程应用中,电化学阻抗的测量比较复杂,应用中存在局限性。基于数据驱动寿命预测是从测试数据的角度出发描述电池性能,分析电池运行过程中的SOC区间、温度、内阻等与寿命的关系[10-11],这种方法以采集的数据为基础,通过数据分析处理方法挖掘其中的隐含信息进行预测,是一种较为实用的预测方法[12-16]。但将实际应用中所有可能的因素全部进行实验测试也是不现实的,所获得的数据往往具有很强的不确定性和不完整性。
针对上述分析,在已有电池寿命预测方法中,存在需要精细测试参数,或未考虑退役动力电池在梯次利用过程的性能突变的问题,已无法满足退役动力电池的寿命预测需求。为能更好地在工程应用中对退役动力电池进行寿命预测,本文提出一种综合考虑数据驱动和电化学外特性的退役电池寿命预测方法,在寿命预测过程中依据容量历史数据和电池的外特性特征参数判定是否出现容量突变,并结合支持向量回归机和粒子滤波的方法对电池容量进行预测,以期获得高精度的电池寿命预测结果,为梯次利用电池储能系统的安全运行提供支撑。
1 梯次利用电池寿命预测需求分析
电池寿命衰减从内部机理分析,主要包括三个方面,分别是电解液分解损耗、正极过渡金属溶出及锂离子的不可逆损失导致的结构变化。另外,电池负极表面也可能产生锂沉积,可能损伤隔膜,导致电池寿命衰减。寿命衰减的外特性表现有容量降低、内阻升高、安全隐患增大、效率降低等。
锂电池的寿命受以下因素影响:
(1)电池的设计与制造。不同电池的材料具有天然不同的使用寿命,比如磷酸铁锂材料由于结构稳定、充放电过程电池结构变化小、材料自身氧化还原能力弱等,循环寿命好于LiCoO2等正极材料。同时,同一种材料的制作或合成方法不同,材料结构完整性、缺陷、表面形貌等都会影响电池的使用寿命。再者,电池的制作过程也会影响电池的寿命,如环境的洁净度、湿度等。
(2)使用环境。电池是电化学储能装置,具有温度敏感的特征,电池的自身发热、温度管理、环境温度都会影响电池的寿命。电池使用环境的湿度不同,对电池的腐蚀性也就不同,对电池的包装及密封性产生的影响程度不同,也会导致电池寿命的不同。使用时电池的振动冲击等也会对电池及电池组的机械性能产生影响,对电池寿命产生影响。
(3)电池的使用工况。电池的充放电深度、工作SOC区间、充放电电流大小、工作频次、使用时间等不同都会影响电池的寿命。对于同一材料体系、同样制作工艺的电池,电池的工作工况不同会对电池的寿命产生非常大的影响,是对电池寿命影响最大的后天因素。
起因、机理及影响因素的多样化导致电池的寿命预测一直是难以解决的问题,而退役动力电池的寿命预测更加复杂,除了前述的电池设计和制造上的原因,即便同一规格型号的汽车电池,在不同汽车上的使用和维护的差异也会引起电池退役时性能状态的不同,电动汽车的运行历程、汽车使用期间的运行工况、电池成组方式、充电方式、管理和维护方法等都会影响电池退役时的性能状态。
图1所示为某电动汽车退役电池的容量衰退曲线,其特征是曲线变化趋势差异大,性能易突变,容易造成安全隐患。因此,梯次利用电池寿命预测方法应具有以下特点:
(1)由于动力电池在退役界面之前的数据无法获取,而其梯次利用后寿命相对较短,因此所构建方法需能在较少数据情况下完成寿命预测。
(2)退役动力电池在梯次利用时,会出现性能突变的情况,需在预测过程中进行突变辨识,并结合辨识结果修正预测模型。
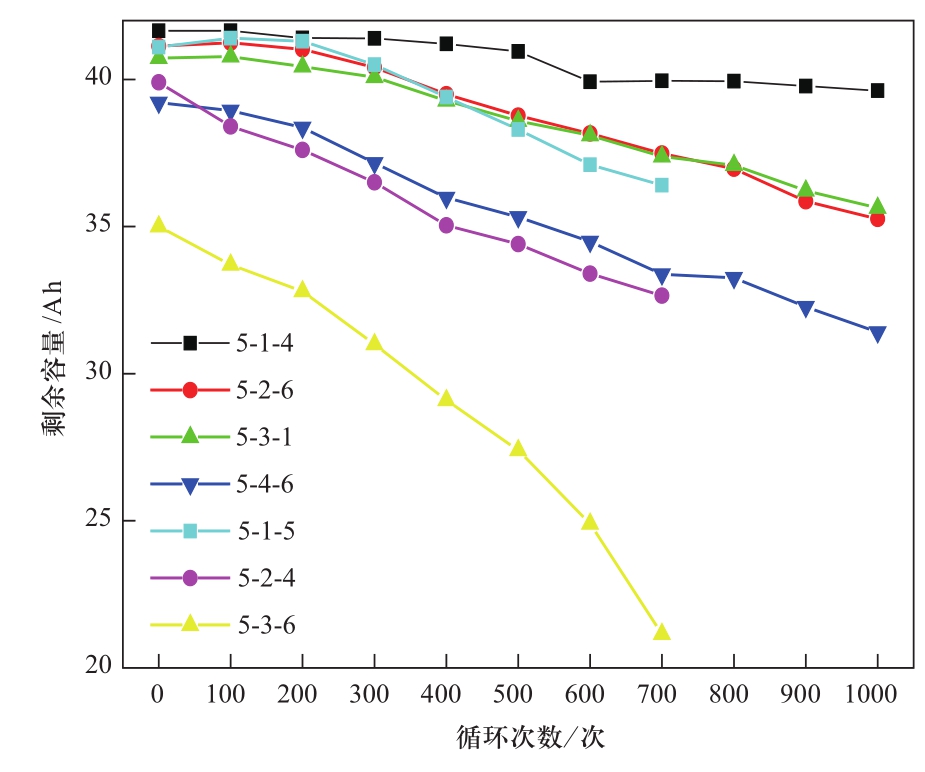
图1 退役电池再循环剩余容量衰退曲线
Fig.1 The decline of residual capacity in different cycles
本文针对上述需求,研究适用于较少数据的寿命预测方法,同时辨识电池循环过程中的性能突变,并分析性能突变中特征参量的变化阈值,提出一种综合考虑历史数据和电池性能的寿命预测方法。
2 综合考虑数据模型和电池性能的寿命预测算法
2.1 基于向量回归机和粒子滤波的预测算法
由于电池容量的衰退曲线呈非线性变化趋势,而支持向量机通过引入空间变化和核技巧,可以将非线性问题的求解转化为线性问题。同时,支持向量机还可以将非线性问题中可能存在的维数问题,通过由核函数向内积运算的转化而解决。在求解回归问题时,即为支持向量回归机(support vector regression,SVR)。因此,本文首先利用支持向量回归机对历史测量数据进行训练建模,利用训练得到的模型预测未来的测量数据,再结合粒子滤波的方法,使得系统状态在预测期间仍能保持实时更新,从而获得系统未来时刻的状态。
粒子滤波算法由序贯重要性采样和重采样构成。序贯重要性采样的实质是将状态的后验概率密度用一系列随机样本的加权和近似,可表述为![]() 其中
其中![]() 为0~k时刻的状态,
为0~k时刻的状态,![]() 是 k 时刻概率密度中密度p( x)所抽取某个样本的集合,样本即为粒子,粒子对应的归一化权值为
是 k 时刻概率密度中密度p( x)所抽取某个样本的集合,样本即为粒子,粒子对应的归一化权值为![]()
在序贯重要性采样中需要考虑粒子数匮乏导致的退化现象,为降低退化中少数具有很大权值的粒子起主导作用的可能性,引入有效粒子Neff来衡量退化现象,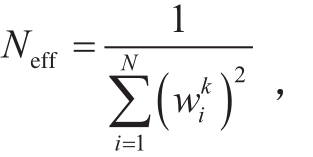 是否进行重采样的依据为有效粒子是否小于阈值Nth,阈值一般取2N/3。若是小于则表示粒子退化严重,需要进行重采样。
是否进行重采样的依据为有效粒子是否小于阈值Nth,阈值一般取2N/3。若是小于则表示粒子退化严重,需要进行重采样。
本文对所采用的粒子滤波算法首先进行初始化, k=0,根据已知概率密度p(x0),采样粒子集![]() 然后进行重要性权值计算,根据
然后进行重要性权值计算,根据![]() 更新粒子权值
更新粒子权值![]()
![]() 归一化重要性权值
归一化重要性权值![]() 若
若![]() 则进行重采样,原来带有的权值样本
则进行重采样,原来带有的权值样本![]() 得到新的等权样本在没有进行重采样的情况下,
得到新的等权样本在没有进行重采样的情况下,![]()
![]() 在进行重采样的情况下,
在进行重采样的情况下,![]() 对算法进行判断是否结束,若是则退出程序,如果没有,则令
对算法进行判断是否结束,若是则退出程序,如果没有,则令![]() 则返回重要性权值计算。
则返回重要性权值计算。
基于向量回归机和粒子滤波的预测算法流程为:
(1)样本预处理。一般对于给定时间序列将其分成训练集和测试集两个部分。在进行建模和预测之前,为了获得更准确的预测结果,同时减少计算的复杂度,避免大数值对训练模型的影响,通常对数据在用于训练之前进行归一化处理。
(2)模型的选择。在支持向量机中,核函数的选择、核函数参数的选择、二次规划参数的选择统称为模型选择。核函数的选择直接关系到模型的性能,合适的模型能够使支持向量机既有好的学习能力,又有好的推广能力。但是现在没有统一的模型选择的标准,只能根据特定的应用背景选择模型。
与其他类型的核函数相比较,径向基函数(radial basis function,RBF)具有参数少、回归精度高等优点,故本文SVR选择RBF核函数,核参数和惩罚因子利用交叉验证寻优。为了减少计算量,采用 Cao氏方法来确定满足条件的最小嵌入维数m。
(3)训练模型。通过回归分析,建立数据与时间的关系,以此实现对未来数据的预测。对于时间序列,根据输入的映射关系,得到支持向量回归的学习样本 。
(4)预测输出。 支持向量回归的时间序列 1 步预测方程为
式中,![]() 支持向量回归的时间序列2步预测方程为
支持向量回归的时间序列2步预测方程为
式中,![]()
由此递推可知,支持向量回归的时间序列p步预测方程为
式中,![]()
(5)状态更新。将上述预测的测量值代入系统的状态空间模型中,用其更新粒子重要性权值,然后进行重采样,获得系统k+1时刻的状态 。
(6)判断是否达到阈值。若达到阈值则退出程序,若否则令k=k+1,返回进行状态更新。
综上所述,基于支持向量回归机和粒子滤波预测方法的流程如图2所示。
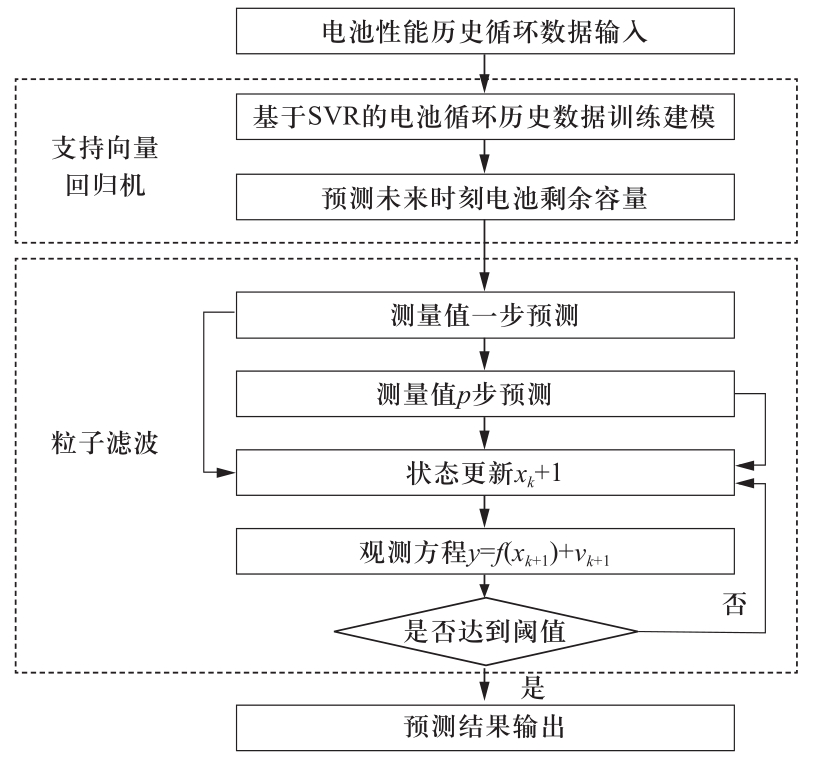
图2 基于支持向量回归机和粒子滤波的预测流程
Fig.2 Prediction based on support vector regression and particle filter
2.2 电池容量突变辨识
由于电池在循环过程中会出现容量跳水的现象,需要对容量突变的时间点进行准确定位,而基于小波变换进行数据分析时,其在时域和频域都具有良好的局部性质,可以聚焦所研究对象的任意细节,并进行分析,因此本文选择小波变换处理电池循环过程中的容量突变。
根据小波变换的应用分类,在理论分析中常用连续小波变换,而离散小波变换更切合工程实践。在分析电池容量突变现象时,需要准确定位容量突变的位置,而离散小波变换在对所分析的数据进行下采样时,采用二进抽取算法。该算法针对每层进行分解后,系数减半,无法实现数据突变的精确辨识,而在离散小波变换基础上提出的静态小波变换在进行变换时不进行下采样,所分析得出的近似和细节系数与原数据采样点位置无较大差别,因此,可以采用离散小波变化进行突变位置辨识。
小波变换的具体定义是:对于一个时间序列函数f(t),函数
称为f(t)的小波变换。这里t是时间,a是分析变换的伸缩尺度,大小与频率相关,b为平移参数,对应着分析事例的起始时间。而![]() 是f(t)的小波变换模。针对突变位置的辨识,在Mallat算法中可用李氏指数a来进行描述,其与所分析数据的小波变换模的关系为
是f(t)的小波变换模。针对突变位置的辨识,在Mallat算法中可用李氏指数a来进行描述,其与所分析数据的小波变换模的关系为
式中,a为李氏指数[17-18],在时间和尺度的平面上,将所有模的极大值点进行连线,并求得其斜率,即为李氏指数。在二进制小波变换中,令a= 2j,对式(1)两边取以2为底的对数,则
在进行奇异点辨识时,判别的理论依据是a是否大于0,在t时刻,小波变换的模极大值由a的正负决定随尺度j的增大而增大或减小。
通过对正负模极大值两条线在低尺度上的交点即可辨识得出奇异点位置。为了保证两条曲线可以相交,其可延伸至尺度接近零处,进而准确定位信号奇异点的位置。
由于小波函数有很多种,在基本小波的选择中,选择较好正交性、双正交性的sym4小波作为基本小波,该小波光滑且接近对称,sym4小波的高层细节部分不会产生明显受小波形状影响的多分辨率分析成分。将电池发生容量突变的数据进行小波变换,利用sym4对突变后的电池容量数据进行5层静态小波分解,并求出各尺度细节系数的局部极大值和极小值,通过绘制模极大值线,判定各点幅值随尺度增大的变化情况,并计算李氏指数,即可确定电池在性能测试过程中的容量突变点。
为了避免仅用容量数据分析引起的误判,还需叠加电池外特性进行突变判别。应结合每100次循环后的性能测试所获得的外特性参数,分析与电池单体性能突变相关的特征参量,确定可引起容量突变的阈值。最终综合考虑电池外特性和基于小波变换的容量突变的结果,判定电池容量突变点。由于在容量发生突变后,电池寿命将加速衰减,因此在寿命预测过程中,对于发生容量突变的电池,将不再进行寿命预测,而是发出电池安全预警。
2.3 基于数据模型和电池性能的电池寿命预测
结合第2.1节和2.2节的分析,本文将支持向量回归机与粒子滤波方法结合起来,在电池容量预测模型中进行应用。针对退役动力电池在寿命末期会出现容量跳水的情况,在寿命预测过程中对容量突变辨识,以提高电池寿命预测的可信度。其预测流程如图3所示。
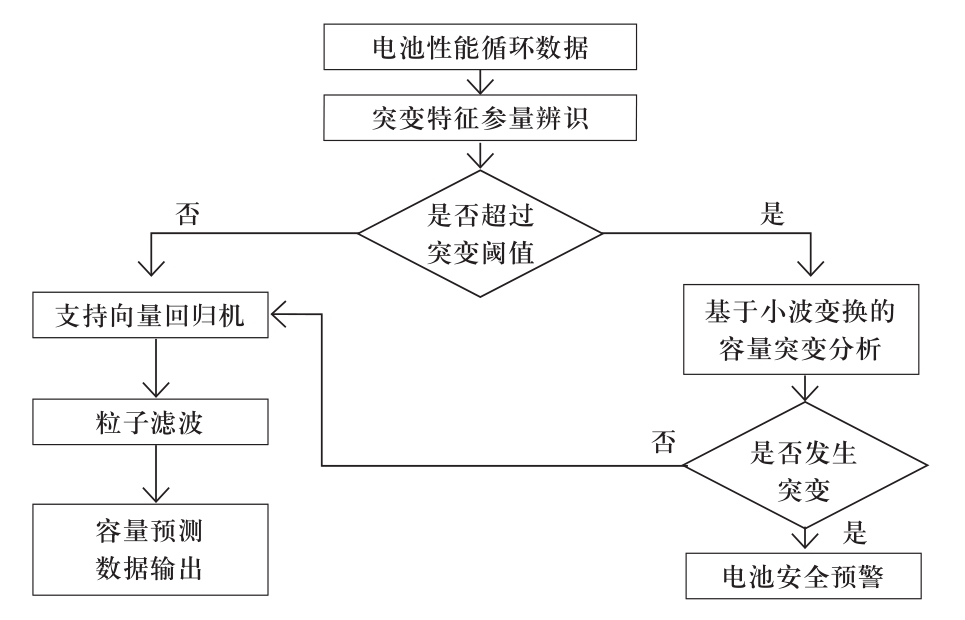
图3 电池容量预测流程
Fig.3 The prediction process of battery capacity
具体的容量预测流程如下:
(1)在电池经过100次循环后,对其进行性能测试,分析退役动力电池的性能循环数据,判定其欧姆内阻增长率是否大于突变阈值。
(2)若步骤1中的欧姆内阻增长率小于突变阈值,则基于支持向量回归机和粒子滤波对其容量进行预测。
(3)若步骤1中的欧姆内阻增长率大于突变阈值,则基于小波变换对其容量进行突变辨识。
(4)若确定步骤3中容量发生突变,则发出电池安全预警,需对其进行更换,若未发生突变,则回到步骤2,对其进行容量预测。
3 算例分析
3.1 数据来源
本文以青岛薛家岛电动公交车充换电站退役的磷酸铁锂电池为研究对象,为保证寿命预测过程中各电池初始性能的一致性,同时又能进行对比分析。首先从退役电池模组中随机选择一个电池模组,电池选自同一辆大巴的同一模组,该电池模组由额定容量为50Ah的电池单体6并4串组成。从每一个并联模块中选择2个单体,共8个单体进行单体性能测试。为测试退役电池应用于储能时的使用寿命,应结合储能工况对电池进行循环试验,在每次循环试验中,首先1/3 C放电至电压≤2.5 V,静置30 min;然后1/2 C充电至电压≥3.65 V,静置30 min;最后1 C放电至电压≤2.5 V,静置30 min。在进行100次循环后,进行性能测试,性能测试主要测量电池单体容量、内阻和功率性能等。
3.2 电池外特性特征参量突变阈值确定
为了能够准确地判定退役电池的容量突变,可结合其外特性进行确认。因此需要分析不同循环次数下电池单体的性能参数。本文选择了初始性能处于不同优劣级别的3块电池,其初始性能如表1所示。
表1 优劣电池单体初始性能
Table 1 The initial performance of different quality cells
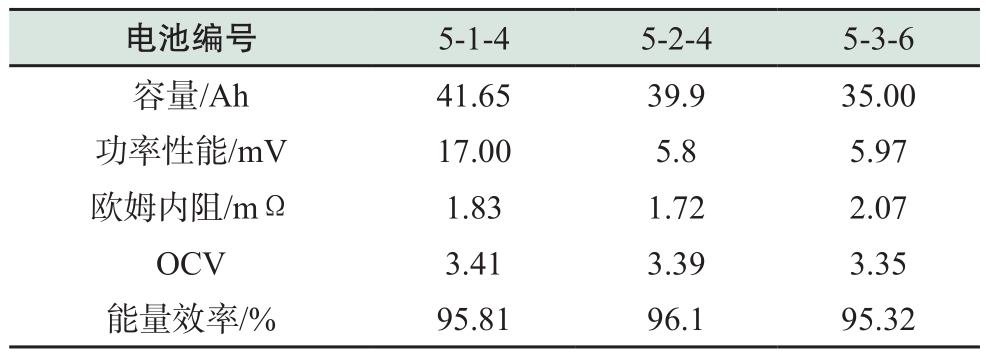
为了便于比较,在分析不同循环次数电池单体性能时,仅对比分析前700次循环的电池性能数据,并将其转化为百分比,以电池单体的初始性能为100%,不同循环次数下各性能参数的数值分别于初始值进行比较,具体结果如图4所示。横坐标是电池性能参数,纵坐标为各性能参数在经过不同循环次数后与初始性能相比的变化率,同一色系随着颜色的加深代表电池单体循环次数的增加。
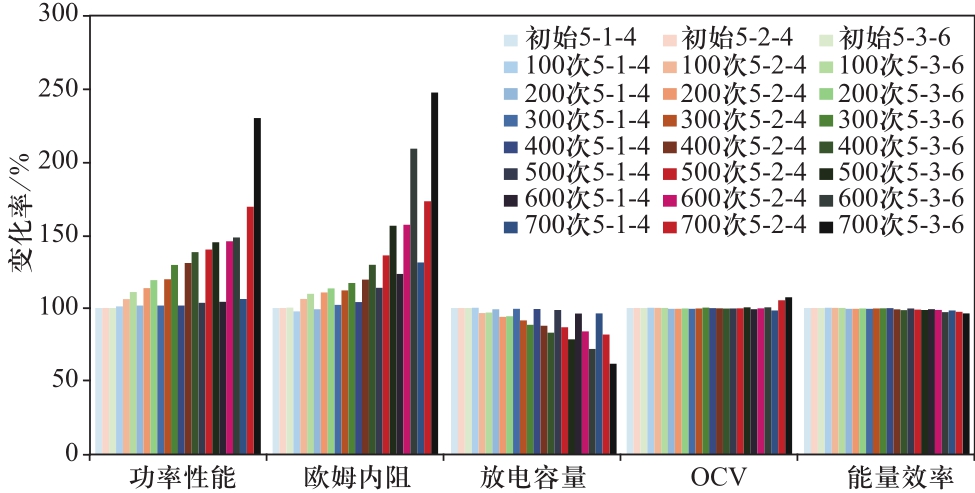
图4 优劣电池单体性能差异对比
Fig.4 The differences in performance compared between different quality cells
从图4可以看出,相比其他2块电池,5-3-6电池单体的欧姆内阻和功率性能均有较大增长,其中欧姆内阻的变化要大于功率性能,因此本文针对该模组的电池单体在进行寿命预测时,选择将欧姆内阻作为容量预测过程发生突变的外特性参数。
为了确定与电池容量突变相关的欧姆内阻阈值,本文结合50%欧姆内阻随循环次数的增加进行了分析,通过分析欧姆内阻随时间的增长率进行判定,欧姆内阻增长率如图5所示。可以看出所分析的7块电池中有3块电池的欧姆内阻在第600次循环中发生了较大增长,但仅有电池单体5-3-6在第600次循环的突变后,电池容量下降到50%以下并迅速衰减到容量为0的状态,而其他电池的欧姆内阻在多次循环过程中的增长率∆Ω均未超过30%,因此可以将导致此类型电池发生容量突变的欧姆内阻增长百分比界限定为30%,在增长率不超过30%的情况下,电池容量发生突变的可能性较小,当欧姆内阻增长率超过30%时,则电池容量极有可能发生容量突变,因此可以将该阈值作为电池容量预测过程中发生突变的判定条件。
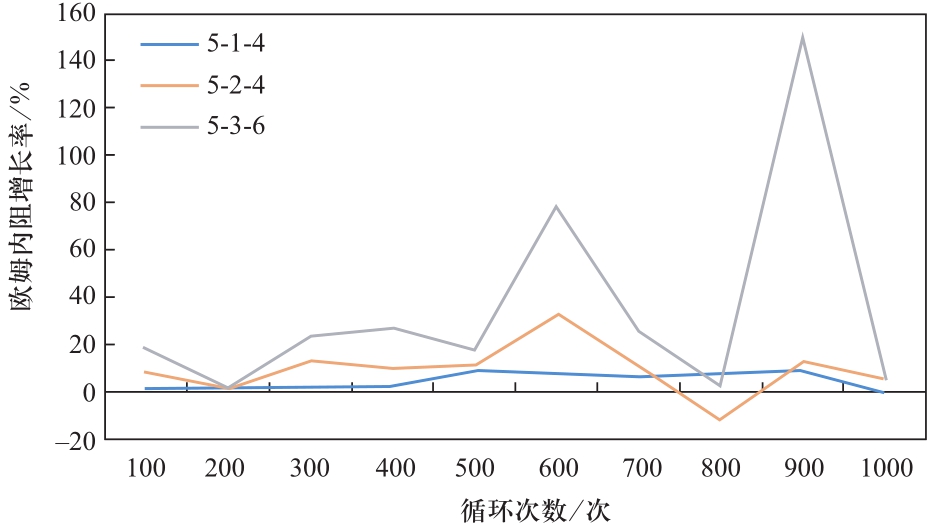
图5 欧姆内阻增长率
Fig.5 The growth rate of ohm internal resistance
3.3 容量跳水单体电池突变点辨识
电池容量的突变点具有数据奇异点的特点,因此结合第3.2节的电池性能特征参量突变阈值的判定结果,本节对5-3-6单体电池每100次循环后的容量进行小波变化,该单体电池在储能工况下的性能循环测试中,共循环了1100次,其整个循环过程中的容量在各尺度细节系数的局部极值点如图6所示。图中由上至下为5层静态小波分解的结果,分别在纵坐标以尺度1至尺度5标注,横坐标为循环次数,单位为100次。
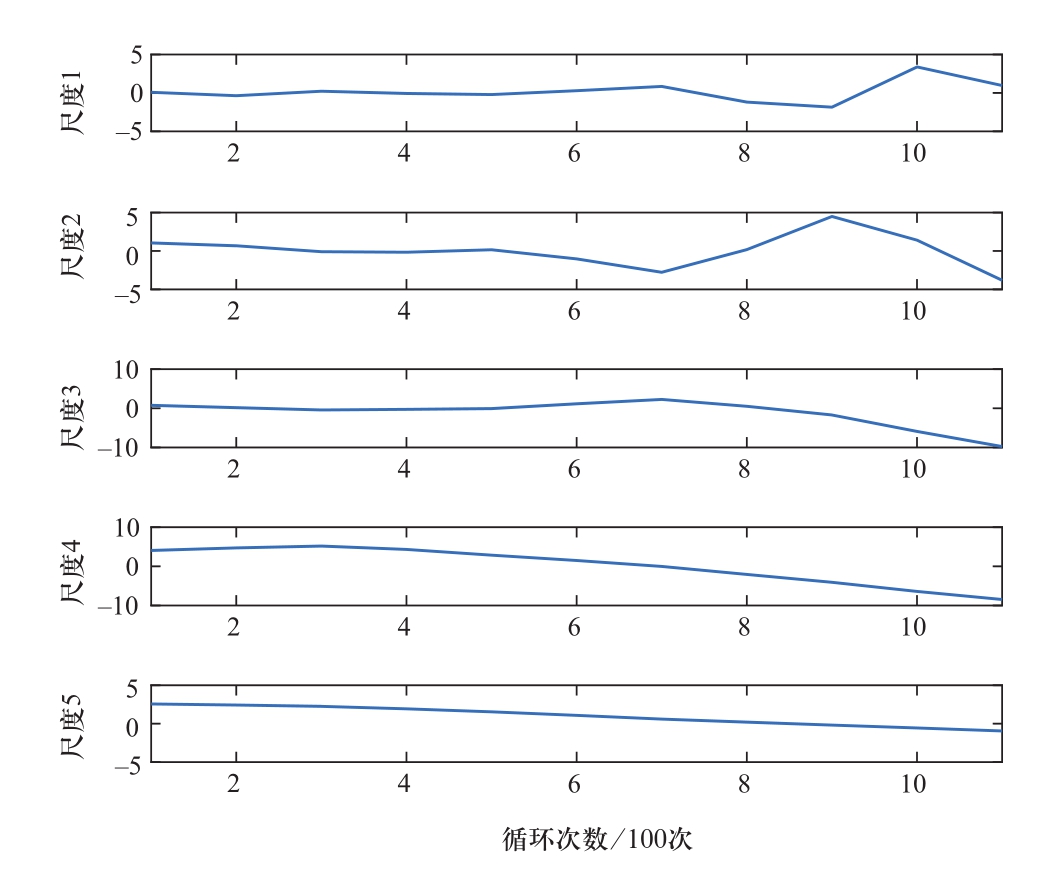
图6 电池容量突变时各尺度细节系数的局部极值点
Fig.6 Local modulus maximum of detail coefficients in battery capacity mutation
通过分析李氏指数与小波变换模的关系,从图中可以判定经过第700次、900次和1000次循环,容量发生了突变。对于退役动力电池进行寿命预测,只需要确认电池循环过程中的第一次容量突变即可,因此,通过小波变换对容量数据的分析可以得出该电池单体在第700次循环后发生了容量突变。
3.4 综合考虑电池性能数据和外特性的电池寿命预测
为了便于预测,本文从进行性能循环测试的8块电池选择了初始剩余容量差别较大的3块电池进行容量预测,选择前700次循环的数据进行训练建模,后300次的数据进行对比分析。同时为了对比本文所提出方法与现阶段常用方法的精确性,在容量预测过程中选择了基于Log函数的容量预测结果进行了对比,对比结果如图7所示。

图7 不同预测方法电池单体容量预测结果对比
Fig.7 Comparison of battery capacity prediction results by different prediction methods
对比分析两种不同方法对电池容量预测的结果,其误差如表2所示。
表2 两种电池容量预测方法的误差
Table 2 Prediction error of battery capacity of two methods
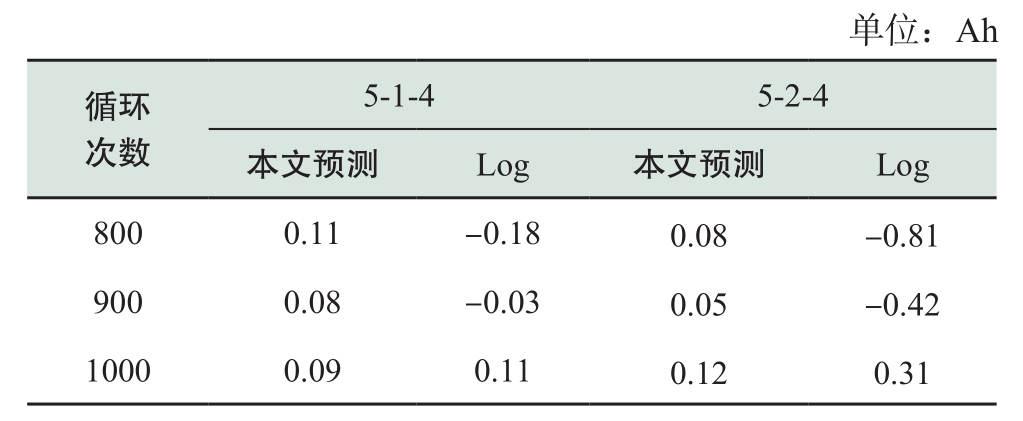
从预测结果可以看出,对于没有发生容量跳水的电池,本文提出的方法优于基于Log的预测方法,可以得到较好的预测结果。但是对于电池单体5-3-6,两种方法对跳水后期的预测偏差较大,但是通过第3.4节的分析,该单体电池的容量和欧姆内阻均已在第700次循环后发生突变,不再进行容量预测,直接发出电池安全预警。
4 结论
本文综合考虑数据模型和电池外特性试验数据,提出了一种综合考虑历史数据和电池外特性的退役电池寿命预测方法,并基于小波变换对电池梯次利用过程中可能存在的容量突变进行辨识,进而对退役电池的寿命终结发出预警。与常用电池寿命预测方法对比,发现本文提出的预测方法可以得到相对较好的结果,并且在容量预测过程中,通过容量突变辨识,避免了分段预测有可能带来的更大误差,同时也为电池安全预警提供了参考。
这种容量预测方法虽然考虑了数据模型和电池外特性,但是由于进行循环测试的电池单体样本较少,该方法存在普适性的问题。因此,进一步研究电池外特性和容量突变之间的关系,有可能会取得新突破或者进一步提高容量预测的可信度。同时,将继续积累电池性能循环测试数据,利用更多的数据对该模型进行验证和提高。
参考文献
[1]Neubauer J, Pesaran A. PHEV/EV Li-ion Battery Second-use Project[R]. USA: National Renewable Energy Laboratory,2010.
[2]Viswanathan V V,Kintner-Meyer M.Second Use of Transportation Batteries:Maximizing The Value of Batteries for Transportation and Grid Services[J].IEEE Transactionson Vehicular Technology,2011,60(7): 2963-2970.
[3]Zhang, Q., & White, R. E.. Capacity Fade Analysis of A Lithium Ion Cell[J]. Journal of Power Sources, 2008, 179(2):793-798.
[4]Gomez, J., Nelson, R., Kalu, E. E., et al. Equivalent Circuit Model Parameters of A High-power Li-ion Battery: Thermal and State of Charge Effects[J]. Journal of Power Sources, 2010,196(10): 4826-4831.
[5]Osaka, T., Nakade, S., Rajamäki, M., et al. Influence of Capacity Fading on Commercial Lithium-ion Battery Impedance[J]. Journal of Power Sources, 2003, 119(6): 929-933.
[6]Li, J., Murphy, E., Winnick, J., et al. Studies on the Cycle Life of Commercial Lithium Ion Batteries During Rapid Charge–discharge Cycling[J]. Journal of Power Sources, 2001, 102(1–2):294-301.
[7]Li, R., Wu, J., Wang, H., et al. Prediction of State of Charge of Lithium-ion Rechargeable Battery with Electrochemical Impedance Spectroscopy Theory[J]. Industrial Electronics and Applications. IEEE. 2010, 684-688.
[8]Lee, S., Kim, J., Lee, J., et al. State-of-charge and Capacity Estimation of Lithium-ion Battery Using a New Opencircuit Voltage Versus State-of-charge[J]. Journal of Power Sources, 2008, 185(2): 1367-1373.
[9]Huet, F. A Review of Impedance Measurements for Determination of the State-of-charge or State-of-health of Secondary Batteries[J]. Journal of Power Sources, 1998, 70(1):59-69.
[10]时玮,姜久春,李索宇,等. 磷酸铁锂电池SOC估算方法研究[J]. 电子测量与仪器学报,2010,24(8): 769-774.Shi Wei, Jiang Jiuchun, Li Suoyu, et al. Research on SOC Estimation for LiFePO4Li-ion Batteries[J]. Journal of Electronic Measurement and Iinstrument, 2010, 24(8): 769-774(in Chinese).
[11]Sauer, D. U., Wenzl, H. Comparison of Different Approaches for Lifetime Prediction of Electrochemical Systems—using Lead-acid Batteries as Example[J]. Journal of Power Sources, 2008, 176(2): 534-546.
[12]Chen, K., Jiang, J., Zheng, F., et al. SOH Estimation for Lithium-ion Batteries: A Cointegration and Error Correction Approach[C]. IEEE International Conference on Prognostics and Health Management. IEEE, 2016, 1-6.
[13]Wenzl, H., Baring-Gould, I., Kaiser, R., et al. Life Prediction of Batteries for Selecting The Technically Most Suitable and Cost Effective Battery[J]. Journal of Power Sources, 2005,144(2): 373-384.
[14]Liaw, B. Y., Jungst, R. G., Nagasubramanian, G., et al.Modeling Capacity Fade in Lithium-ion Cells[J]. Journal of Power Sources, 2005, 140(1): 157-161.
[15]Wright, R. B., Motloch, C. G., Belt, J. R., et al. Calendar and Cycle-life Studies of Advanced Technology Development Program Generation 1 Lithium-ion Batteries[J]. Journal of Power Sources, 2002, 110(2): 445-470.
[16]Parthiban, T., Ravi, R., & Kalaiselvi, N.. Exploration of Artificial Neural Network [ANN]to Predict the Electrochemical Characteristics of Lithium-ion Cells[J]. Electrochimica Acta, 2008, 53(4): 1877-1882.
[17]Mallat S, Zhou S F. Characterization of Signal from Multiscale Edges[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1992, 14(7): 710-732.
[18]胡广书. 现代信号处理教程[M]. 北京:清华大学出版社,2004.Hu Guangshu. Modern Signal Processing Tutorial[M]. Beijing:Tsinghua University Press,2004(in Chinese).
Research on Life Prediction for Second-Use of Electric Vehicle Power Battery
WANG Kai-rang1,2, BAI Kai1,2, LI Na1,2, GONG Yu1,2, SHI Xue-wei1,3
(1. Grid-connected Operation Technology for Wind-Solar-Storage Hybrid System State Grid Corporation Key Laboratory,Xicheng District, Beijing 100045, China;2. State Grid Jibei Electric Power Research Institute, North China Electric Power Research Institute Co., Ltd.,Xicheng District, Beijing 100045, China;3. State Grid Xinyuan Zhangjiakou Wind, Photoboltaic, Storge and Transmission Pilot Power Station Co., Ltd.,Zhangjiakou 075000, Hebei Province, China)
Abstract:With the rapid development of electric vehicles in China, the continuous retirement of multitudinous power batteries has brought opportunities to reduce the cost of energy storage. But there is no definitive conclusion for the performance change rules of the reusable battery for power storage. In this paper, the retired battery of Xuejiadao of Qingdao electric bus charging station is taken as the research object. The support vector regression machine and particle filter are applied to the battery capacity prediction, and the capacity mutation of the battery is identified by combining the wavelet transform and the characteristics of the battery in the prediction process. A prediction method of reused life of retired batteries based on sampling test is proposed and verified. The results show that the method can improve the prediction accuracy of the capacity decline path and reduce the effect of the capacity mutation of the decommissioned battery on the prediction accuracy, which is of practical significance for the cascade utilization of the decommissioned power battery.
Keywords:retired battery; second-use; power energy storage;lifetime prediction
Project Supported by National Key Reaearch and Development Program of China(2016YFB0900500).

王开让
作者简介:
王开让(1987),男,博士,工程师,研究方向为电池成组应用与管理。E-mail:krwang798@qq.com。
白恺(1971),女,硕士,教授级高级工程师,从事新能源发电及并网、储能技术等研究工作。
李娜(1986),女,硕士,高级工程师,研究方向为动力电池梯次利用及管理。
(责任编辑 赵杨)
