0 引言
全球新能源汽车行业当前正处于蓬勃发展的时期。世界主要工业国均出台了相关产业政策大力推进本国新能源汽车的发展,我国也将制定禁止生产销售燃油车时间表。随着电动汽车的大规模推广,动力电池的产量也大幅提高,随之而来的是退役电动汽车动力电池的处理问题。当锂离子电池容量衰减到原有容量80%时,就不再适合继续在电动汽车上使用。在电池外观完好、没有破损、各功能元件有效的情况下,可进行二次利用,作为太阳能、风能等清洁能源以及电网、微网的储能装置[1][2]。
目前,梯次利用电池组成的储能系统在削峰填谷、平抑分布式电源出力波动等场合发挥着重要作用,这对电池系统的调度及控制提出了非常高的要求。大规模梯次利用电池组的建模与仿真成为电池系统研究的重要内容。
范刘洋等人搭建了考虑不一致性的电池储能系统的详细模型,并将该模型应用于储能系统平抑风电波动的仿真[3]。但是该方法的缺点是需要事先辨识每个单体的参数,并计算每个单体的端电压,计算机仿真模型复杂,占用资源多,难实现大规模的串联电池仿真。陆秋瑜等人根据厂家提供的数据即可对Thevenin模型中的开路电压(open circuit voltage, OCV)和阻抗参数进行拟合,无需进行复杂且耗时的阻抗频谱或脉冲电流实验[4]。但对于梯次利用电池组来说,厂家的参数已经不再适用,参数拟合只能依赖于足够的储能电站性能测试数据。而针对大规模电池储能电站的相关实验和测试条件目前尚不够成熟,该方法较难实现。叶小晖等人建立了电池储能系统的多时间尺度仿真模型[5],但是其将电池组当作一个阻容参数恒定的大电池,并做了很多简化,精度较差。该方法减少了电池参数辨识,但是不能够反应串联电池组内参数的不一致性。Sun Fengchun等人首先选定一个“标准电池”,然后利用数据驱动的方法识别电池组内其他电池和标准电池的差异,并用不同时间尺度对标准电池和其他电池进行仿真以减少运算量[6]。但该文中仅使用电动汽车工况,该方法对于储能工况的适用性没有说明。另外,还有一些文献也只针对电动汽车电池组进行建模仿真[7-9]。由于梯次利用电池组的使用场景的不同,电动汽车电池组建模仿真方法不能直接应用。
考虑梯次利用电池系统实际情况,针对大规模梯次利用电池组的建模与仿真时电池参数获取困难的问题,本文提出了串联电池组参数在线辨识的仿真方法。
1 电池模型和参数辨识
1.1 电池单体模型
为建立电池组仿真模型,需首先确定单体模型。Thevenin模型能够较好地体现电池的静态与动态性能,并可准确地反映电池电动势与端电压的关系,从而使估计有较高的精度[10]。和二阶RC模型相比,Thevenin模型可以减少处理器的运算,更易于工程实现。Thevenin模型等效电路如图1所示。图中,Uoc为电池开路电压,Ro为电池的欧姆内阻,Rp为电池的极化内阻,Cp为极化电容,UL为电池端电压,IL为电流,假设充电为正。将极化电压Up作为一个中间状态量,电流IL作为输入量,端电压UL作为输出量,离散的状态空间方程可以描述为式(1)。
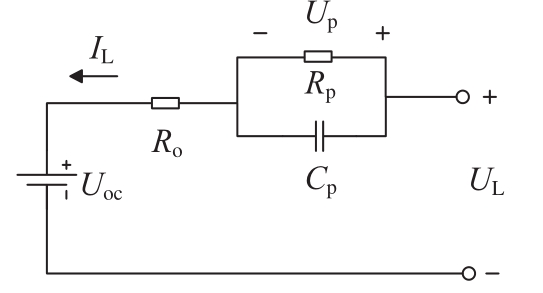
图1 Thevenin模型等效电路图
Fig.1 Thevenin model equivalent circuit diagram
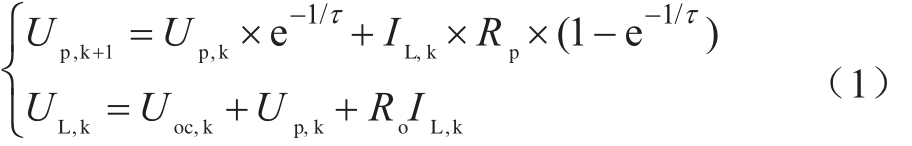
其中,τ =RpCp为极化时间常数,下角标 k 表示k时刻。
根据Thevenin模型和式(1)可知,待辨别的电池参数有开路电压Uoc,欧姆内阻Ro,极化电阻Rp和极化电容Cp。目前普遍通过离线的参数辨识实验进行参数的辨识。但是该方法需要长时间静置,并且这些参数与电池的荷电状态(state of charge, SOC)、温度以及老化状态有关,而且充电和放电时这些参数的值也不同。对于大规模梯次利用电池组来说,用户手册中的电池参数已经不再适用,通过大量且耗时的实验来构建繁冗复杂的电池参数表显然也不现实。
1.2 参数在线辨识
递推最小二乘法算法(recursive least squares,RLS)具有良好的在线学习和自适应能力,在系统辨识、自适应控制、在线学习系统、数据挖掘等方面具有广泛的应用。下面利用递推最小二乘法对电池参数进行在线辨识。
根据电池等效电路模型,可以写出s域中UL和IL的关系:
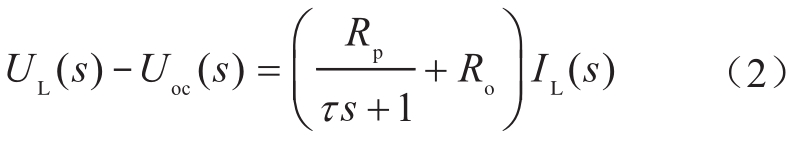
利用双线性变换公式(式3)可以将式(2)离散化成式(4)。
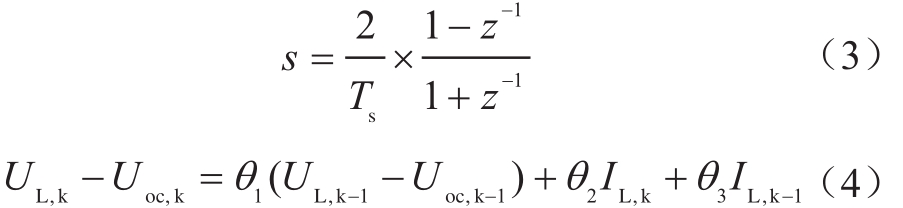
其中![]()
![]()
假设采样时间Ts间隔很小,那么在一个采样时间内OCV可以视作常值[11],则式(4)可以写作如下形式:
假设![]() 并将其当作待辨识的一个参数,得到
并将其当作待辨识的一个参数,得到
定义yk=UL,k为系统输出,θ=[θ1, θ2, θ3, θ4]T为待辨识的参数向量,![]() 为数据向量,应用递推最小二乘法公式(式7)即可求出待辨识参数θ,进而根据式(8)求出Ro,Rp,Cp和Uoc。
为数据向量,应用递推最小二乘法公式(式7)即可求出待辨识参数θ,进而根据式(8)求出Ro,Rp,Cp和Uoc。
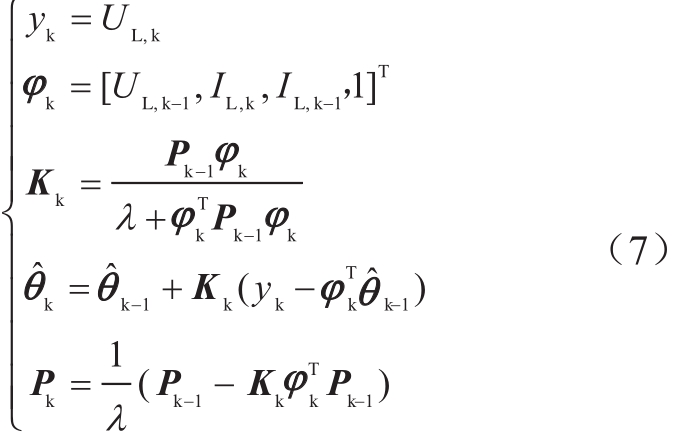
其中![]() 为参数估计值,K为增益系数,P为协方差矩阵,λ为遗忘因子。为了避免数据饱和,加强新数据对当前辨识结果的影响,λ在本文中设置为0.985。
为参数估计值,K为增益系数,P为协方差矩阵,λ为遗忘因子。为了避免数据饱和,加强新数据对当前辨识结果的影响,λ在本文中设置为0.985。

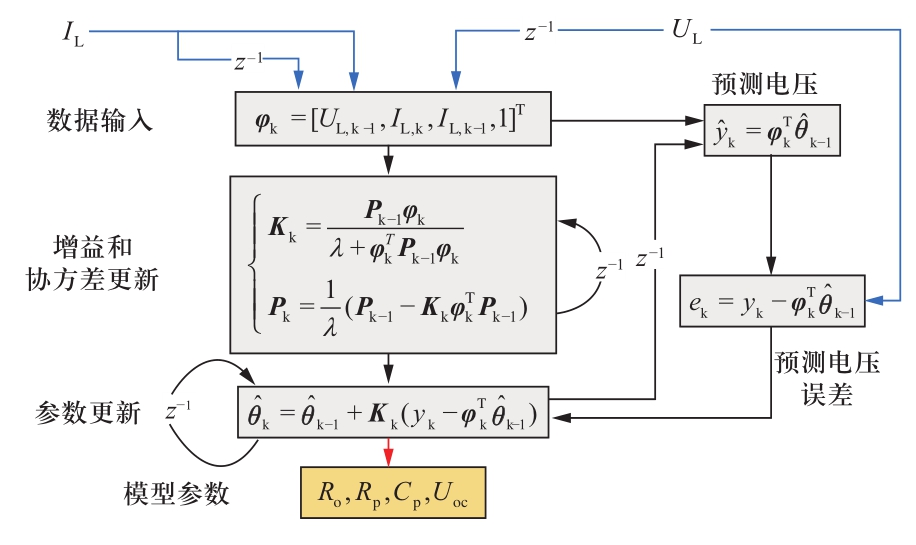
图2 基于RLS的参数在线辨识过程
Fig.2 Online identification of parameters based on RLS
(注:z-1为单位延迟算子)
由此可以求得当前时刻下的阻容参数和当前SOC下的开路电压。如果电池组从SOC=100%开始执行动态工况至SOC=0,便可以得到全SOC区间的阻容参数和OCV-SOC曲线,从而解决大规模电池组模型参数获取困难的问题,同时这些参数也可以应用到传统的离线模型。
2 串联电池组建模和仿真
2.1 串联电池组模型
从电池单体模型到串联电池组模型一直是电池研究中的难点,目前普遍使用的串联电池组模型有两种[12]。一种是整体模型,将电池组等效成一个大的“电池单体”,忽略组内的结构及差异,利用单体电池模型结构,直接对电池组总电压和总电流进行参数辨识,得到电池组等效参数并进行端电压的仿真。另外一种是组合模型,该模型由若干结构相同、参数不同的电池单体模块串联而成,各单体电流相同,独立进行参数辨识和端电压仿真,单体端电压直接叠加即为电池组外电压。
2.2 DST工况在线仿真
为了确定一种最适合大规模梯次利用电池组仿真的模型,本文将基于RLS的参数在线辨识方法分别和两种电池组模型进行结合。使用Arbin BTS2000电池测试设备对电池组进行测试(采样频率1 Hz),将测试数据输入模型进行仿真,对比两种模型的精度。所利用的电池为从某型号纯电动汽车退役下来的磷酸铁锂电池组,该电池组由20只标称电压3.2 V、标称容量为180 Ah的单体串联而成,目前各单体已经出现不同程度的衰减。
首先将电池组充电至任意一只单体达到充电截止电压,充分静置。对该串联电池组循环执行动态应力测试(dynamic stress test, DST)工况,至任意一只单体达到放电截止电压停止。单个循环的DST工况如图3所示,100%功率处的电流设置为100 A。
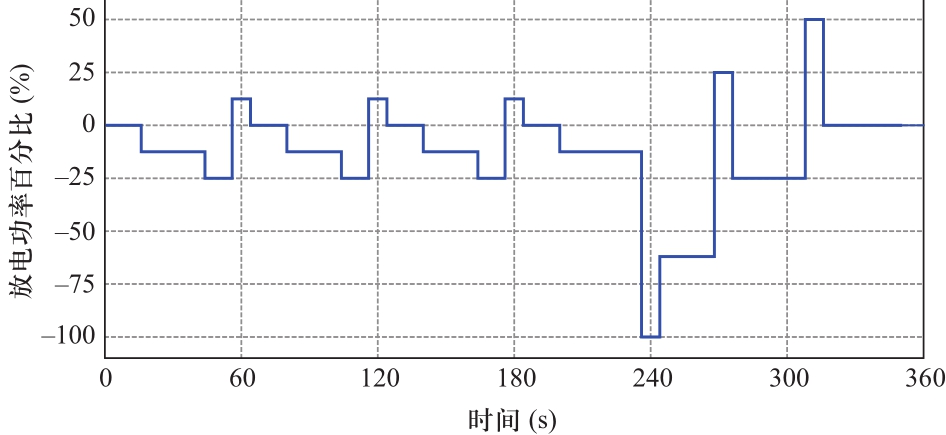
图3 单个循环的DST工况
Fig.3 Single-cycle DST conditions
利用RLS方法辨识得到的其中一只单体的开路电压和欧姆内阻如图4和图5所示。利用离线的参数辨识实验得到的辨识值同样显示在图中。整体模型和组合模型的端电压仿真结果如图6~图8所示。
在工况开始时,由于参数初值的设定和真实值之间存在较大差异,开路电压OCV和欧姆内阻Ro均出现较大误差。随着工况的执行,RLS算法迅速收敛,参数辨识结果也随之迅速收敛到真实值附近。从图4和图5中可以看出,基于RLS的参数在线辨识方法具有较快的收敛速度和较高的精度,其辨识结果和离线辨识实验的结果基本重合。极化内阻和极化电容的辨识结果类似,在此不再赘述。
从图6和图7中可以看出,对于该电池组的仿真,除去开始算法收敛和末尾端电压陡降造成较大误差外,组合模型的误差一般在300 mV(相对误差0.5%)以内,整体模型的误差则在100 mV(相对误差0.2%)以内。整体模型仿真时,当总电压和总电流输入模型后,仅进行一次参数辨识和端电压计算,避免了组合模型在计算电池组总电压时各单体端电压相加造成的误差叠加。图8放大了整体模型6500 s~8000 s之间的仿真结果。可以看出,基于RLS的串联电池组整体模型对真实电压的追踪具有相当高的快速性和准确性。
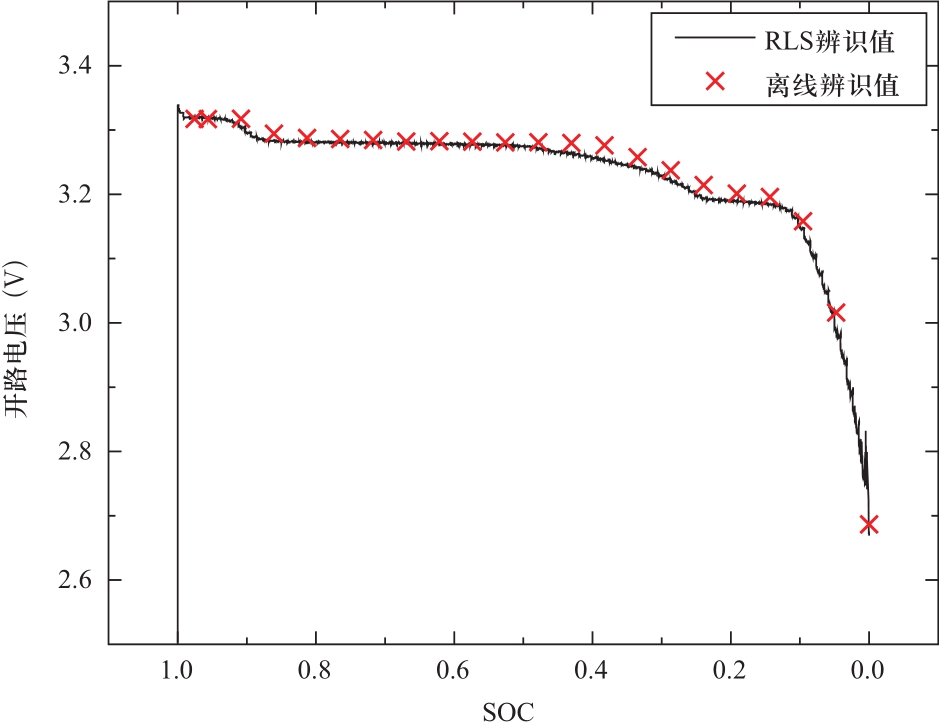
图4 开路电压OCV辨识结果
Fig.4 Identification result of open circuit voltage

图5 欧姆内阻Ro辨识结果
Fig.5 Identification result of Ro
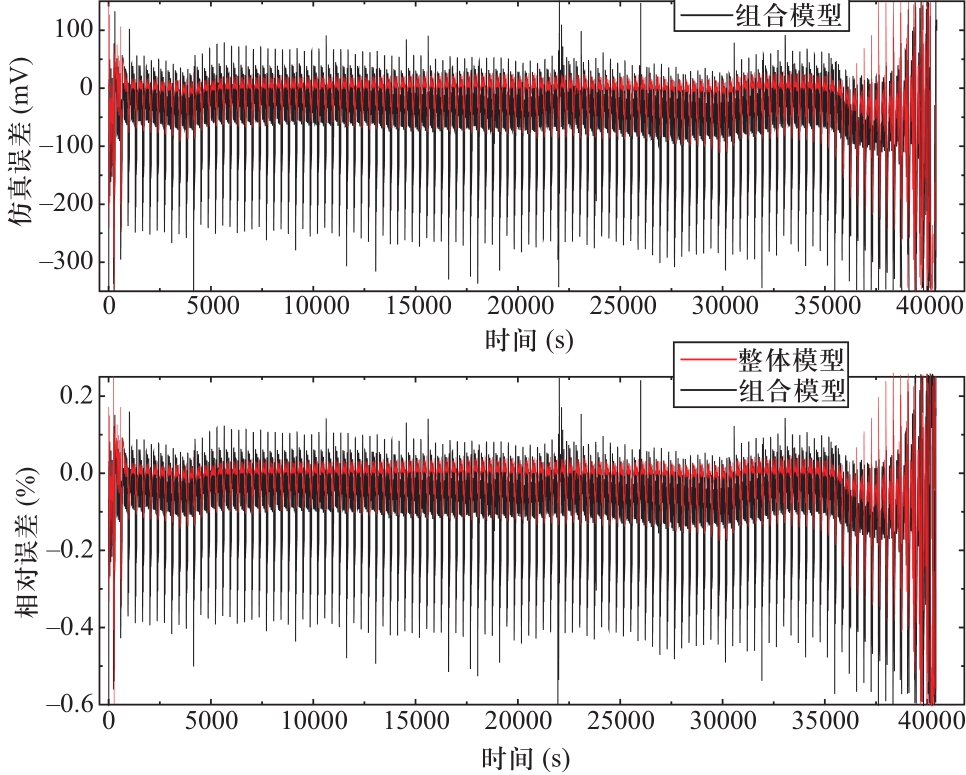
图6 DST工况下在线仿真结果
Fig.6 Online simulation results under DST conditions
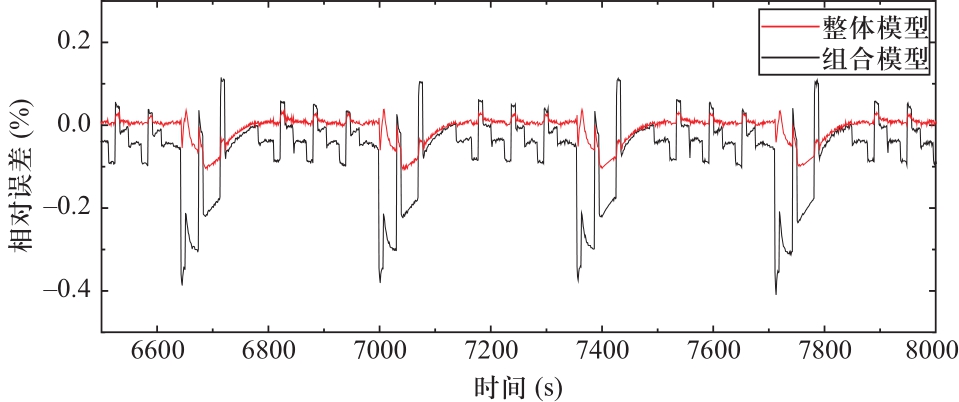
图7 仿真相对误差局部放大图
Fig.7 Partial enlargement of relative error
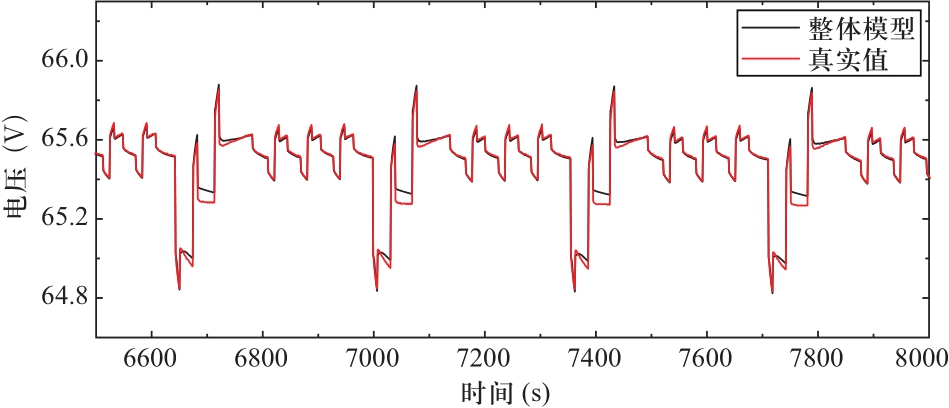
图8 整体模型仿真结果局部放大图
Fig.8 Partial enlargement of overall model simulation results
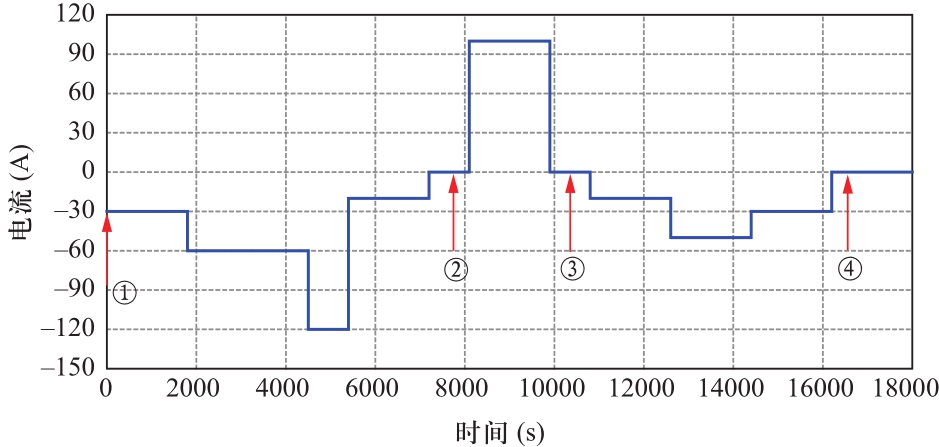
图9 储能工况及添加的白噪声处示意图
Fig.9 Schematic diagram of energy storage conditions and added white noise
2.3 储能工况在线仿真
储能系统中的工况往往存在恒流阶段,图9为利用文献[13]所提出的工况提取方法提取的风电场储能电池典型工况。将电池组从满电状态执行该工况一次,利用实验数据以及RLS算法对整体模型进行仿真,结果如图10所示。
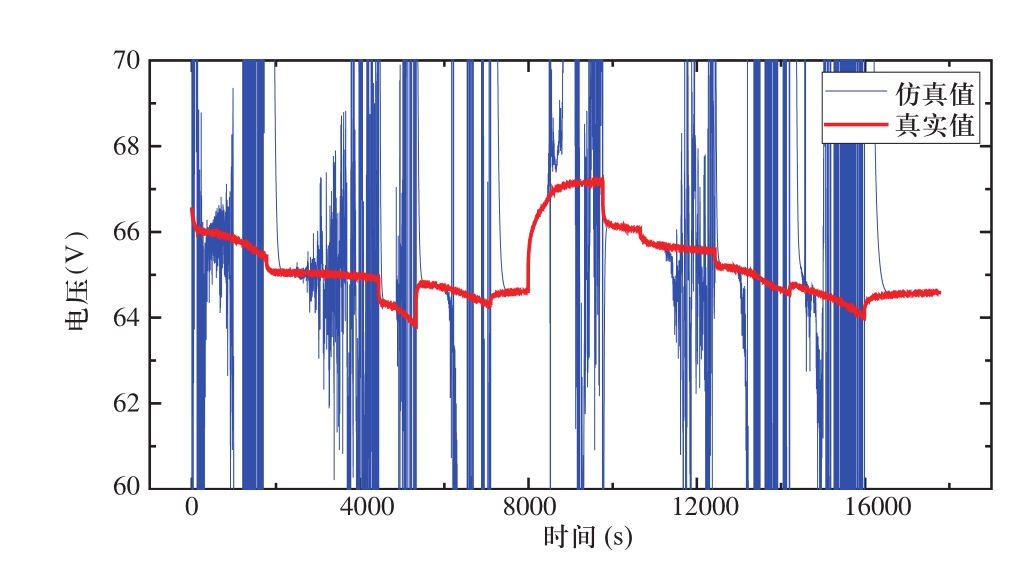
图10 储能工况在线仿真结果
Fig.10 Online simulation results under energy storage conditions
由仿真结果可以看出,每当电流出现变化时仿真电压能够收敛到真实值,随着恒流充放电的进行,仿真误差逐渐增大,最终出现了发散。根据最小二乘法的推导过程,数据矩阵Φ(式9)必须满秩[14],即满足rank(Φ)=4。
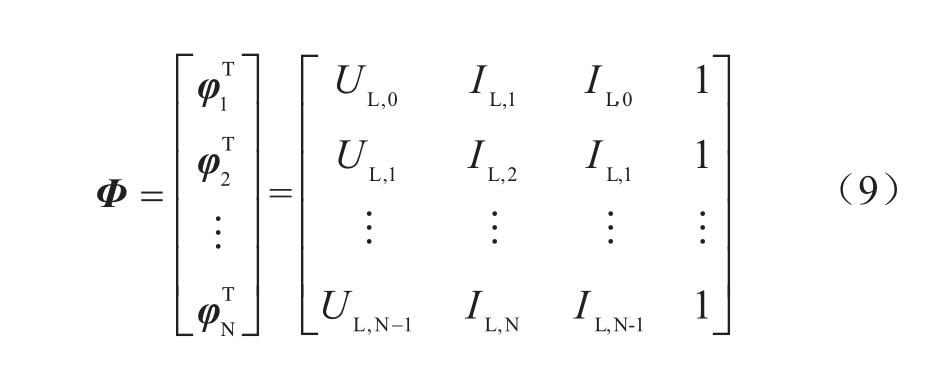
也就是说![]() 这就要求在0~N的时间内,至少存在一个时刻k使得
这就要求在0~N的时间内,至少存在一个时刻k使得![]() 而恒流阶段不满足此条件,导致结果发散。零均值白噪声可以用作激励任何系统的输入信号[15]。为了使RLS参数辨识能够应用到储能电池典型工况的在线仿真,考虑在电池静置600 s时(图9红色箭头处)利用充放电设备加入60 s的零均值白噪声,作为持续激励信号,进行在线参数辨识。在电流恒流阶段使用最近一次辨识得到的60 s末的阻容参数。由于OCV和SOC的对应关系,在电流继续放电时最近一次辨识得到OCV值不能够继续使用,这里使用上一小节中DST工况下在线得到的OCV-SOC曲线。再次进行实验和仿真,结果如图11所示。
而恒流阶段不满足此条件,导致结果发散。零均值白噪声可以用作激励任何系统的输入信号[15]。为了使RLS参数辨识能够应用到储能电池典型工况的在线仿真,考虑在电池静置600 s时(图9红色箭头处)利用充放电设备加入60 s的零均值白噪声,作为持续激励信号,进行在线参数辨识。在电流恒流阶段使用最近一次辨识得到的60 s末的阻容参数。由于OCV和SOC的对应关系,在电流继续放电时最近一次辨识得到OCV值不能够继续使用,这里使用上一小节中DST工况下在线得到的OCV-SOC曲线。再次进行实验和仿真,结果如图11所示。
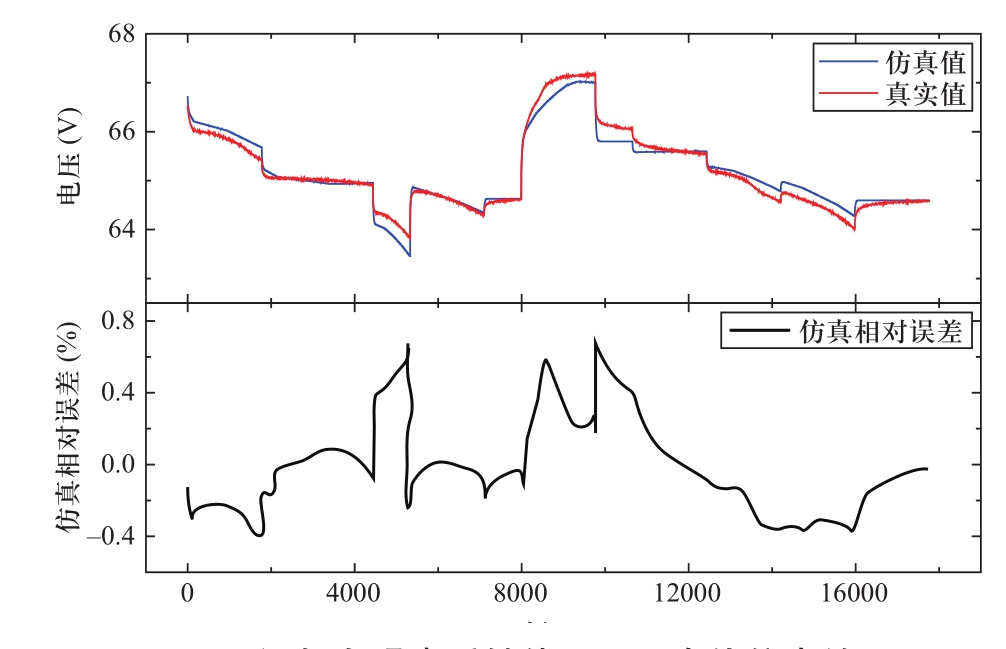
图11 添加白噪声后储能工况下在线仿真结果
Fig.11 Online simulation results under energy storage conditions after adding white noise
由结果可以看出,该方法避免了直接应用RLS出现发散的缺点。但是在电流大倍率充放电时容易出现较大误差。这是由于在不同的电流倍率下电池的参数出现较大变化[16],辨识得到的阻容参数已经和大倍率充放电时电池的实际阻容参数出现了较大差异,进而导致误差增大。但同时可以看出,该方法最大相对误差仍在0.8%以内。对于无法进行离线参数辨识实验的电池系统,该方法是一种具有较高精度电池组建模仿真方法。
3 结论
大规模梯次利用电池组建模仿真主要存在以下难点:储能系统中电池数目增加时,电池参数辨识的工作量也随之增加,到达一定规模后,若要通过离线辨识实验得到储能电池组中的所有单体电池参数则不太实际。针对上述问题,本文提出了参数在线辨识的仿真方法,并得到如下结论:
(1)对于电流变化剧烈工况下的电池组在线仿真,本文将电池组视作一个整体,利用RLS进行在线的参数辨识,电池组整体模型端电压的仿真相对误差在±0.2%以内。
(2)对于恒流工况下电池组的在线仿真,在静置阶段添加白噪声作为参数辨识的激励输入,利用RLS快速、在线辨识参数,以此解决无法进行离线参数辨识实验的问题。该方法仿真相对误差在±0.8%以内。
参考文献
[1]李建林,修晓青,刘道坦,等. 计及政策激励的退役动力电池储能系统梯次应用研究[J]. 高电压技术,2015,41(8):2562-2568.Li Jianlin, Xiu Xiaoqing, Liu Daotan, et al. Research on Second Use of Retired Electric Vehicle Battery Energy Storage System Considering Policy Incentive[J]. High Voltage Engineering, 2015, 41(8): 2562-2568(in Chinese).
[2]王泽众,李家辉. 电池梯次利用储能装置在电动汽车充换电站中的应用[J]. 电气自动化,2012,34(6):49-50.Wang Zezhong, Li Jiahui. Application of Battery Cascade Utilization Device in EV Battery Charging and Swapping Station. Electrical Automation,2012, 34(6): 49-50.
[3]范刘洋,汪可友,张宝群,等. 考虑电池组不一致性的储能系统建模及仿真[J]. 电力系统自动化,2016(3):110-115.Fan Liuyang, Wang Keyou, Zhang Baoqun, et al. Modeling and Simulation of Battery Energy Storage System Considering Intrinsic Inconsistency. Automation of Electric Power System,2016(3): 110-115.
[4]陆秋瑜,胡伟,郑乐,等. 多时间尺度的电池储能系统建模及分析应用[J]. 中国电机工程学报,2013,33(16):86-93.Lu Qiuyu, Hu Wei, Zheng Le, et al. Modeling and Analysis of Battery Energy Storage System in Multi-time Scales Application. Proceeding of the CSEE, 2013, 33(16): 86-93.
[5]叶小晖,刘涛,吴国旸,等. 电池储能系统的多时间尺度仿真建模研究及大规模并网特性分析[J]. 中国电机工程学报,2015,35(11):2635-2644.Ye Xiaohui, Liu Tao, Wu Guoyang, et al. Multi-time Scale Simulation Modeling and Characteristic Analysis of Large-scale Grid-connected Battery Energy Storage System.Proceedings of the CSEE,2015, 35(11): 2635-2644.
[6]Sun F, Xiong R. A novel dual-scale cell state-of-charge estimation approach for series-connected battery pack used in electric vehicles[J]. Journal of Power Sources, 2015, 274: 582-594.
[7]熊瑞,何洪文,许永莉,等. 电动汽车用动力电池组建模和参数辨识方法[J]. 吉林大学学报(工),2012,42(4):809-815.Xiong Rui, He Hongwen, Xu Yongli, et al. Modeling and Parameter Identification Approach for Power Battery Pack Used in Electric Vehicle. Journal of Jilin University(Engineering and Technology Edition),2012, 42(4): 809-815.
[8]Fotouhi A, Auger D J, Propp K, et al. Accuracy Versus Simplicity in Online Battery Model Identification[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2016,PP(99): 1-12.
[9]陈哲群. 磷酸铁锂电池建模仿真与均衡策略研究[D]. 深圳大学,2017.
[10]Liaw B Y, Nagasubramanian G, Jungst R G, et al. Modeling of lithium ion cells—A simple equivalent-circuit model approach[J]. Solid State Ionics, 2004, 175(1–4): 835-839.
[11]Xiong R, He H, Sun F, et al. Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach[J]. Energies, 2012, 5(5): 1455-1469.
[12]姜君. 锂离子电池串并联成组优化研究[D]. 北京交通大学,2013.
[13]仲金龙,张建文,周贤姣,等. 风电场储能电池典型工况提取研究[J]. 电测与仪表,2015,52(9):125-128.Zhong Jinlong, Zhang Jianwen, Zhou Xianjiao, et al. Research on the Typical Working Condition of Energy Storage Batteries for Wind Farms. Electrical Measurement & Instrumentation,2015, 52(9): 125-128.
[14]庞中华,崔红. 系统辨识与自适应控制MATLAB仿真[M].北京航空航天大学出版社,2013,28-31.
[15]丁锋. 系统辨识(3):辨识精度与辨识基本问题[J]. 南京信息工程大学学报(自然科学版),2011,03(3):193-226.Ding Feng.System Identification.Part C: Identification Accuracy and Basic Problems. Journal of Nanjing University of Information Science and Technology: Natural Science Edition, 2011, 3(3): 193-226.
[16]Liu S, Jiang J, Shi W, et al. Butler–Volmer-Equation-Based Electrical Model for High-Power Lithium Titanate Batteries Used in Electric Vehicles[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7557-7568.
A New Modeling and Simulation Method for Large Scale Second-Use Battery Pack
DONG Xi-le1,2, ZHANG Cai-ping1,2, JIANG Jiu-chun1,2
(1. National Active Distribution Network Technology Research Center (NANTRC), Beijing Jiaotong University,Haidian District, Beijing 100044, China;2. Collaborative Innovation Center of Electric Vehicles in Beijing, Haidian District, Beijing 100044, China)
Abstract:In order to solve the problems in obtaining battery parameters during modeling of large-scale second-use battery packs, the battery parameters are identified on-line using recursive least squares method based on the Thevenin model of lithium-ion battery. The combination model and the overall model of the series-connected lithium-ion battery pack are built to verify the accuracy of the online parameter identification under dynamic stress test conditions. The simulation accuracy of terminal voltage is within 0.5% in combination model, and within 0.2% in overall model. Combining the typical conditions of the energy storage battery, using the overall model, adding white noise as a stimulus under constant current, the feasibility of online parameter identification is verified and the relative error is within 0.8%. It provides the research basis for the modeling and simulation of large-scale second-use battery packs.
Keywords:second-use; battery pack; modeling; online parameter identification
Project Supported by National Key Research and Development Program of China (2018YFB0905304).

董喜乐
作者简介:
董喜乐(1993),男,硕士研究生,主要研究方向为电池建模、电池状态估计。E-Mail:16121433@bjtu.edu.cn。
张彩萍(1982),女,教授,博士生导师,主要研究方向为电动汽车动力电池和储能电池在电力系统中的应用。E-Mail:zhangcaiping@bjtu.edu.cn。
姜久春(1973),男,教授,博士生导师,主要研究方向为电动汽车充电站、电动汽车电池管理系统、微网技术。E-Mail:jcjiang@bjtu.edu.cn。
(责任编辑 张鹏)
