0 引言

随着全球经济发展，能源危机逐步加剧，环境问题也日益突出，世界各国就应对气候变化、实现碳中和逐渐达成共识[1-4]。在“碳达峰、碳中和”目标的引领下，新能源锂离子电池产业作为绿色产业的重要组成部分，迎来了前所未有的高速增长[5-6]。锂离子电池是目前综合性能最好的电池体系，具有比能高、寿命长、污染少、体积小等优点[7-10]。近年来，国务院、工业和信息化部、发展改革委等陆续出台《锂离子电池行业规范条件（2021年本）》《工业领域碳达峰实施方案》《“十四五”新型储能发展实施方案》等技术指南和发展方案[11]。在国家政策支持和经济补贴下，中国锂离子电池产业飞速发展。据统计，2022年中国锂离子电池出货量达到660.8 GWh，同比增长97.7%，占全球锂离子电池总体出货量的69.0%。预计到2023年，中国锂离子电池市场出货量将超过1 TWh。

在日常使用和存储过程中，锂离子电池受多应力耦合作用发生老化，导致其内部可用锂离子损失、正负极活性材料损失以及阻抗增加[12-15]。相应地，电池容量和功率性能也逐渐下降，甚至可能引发漏液和内短路等安全问题，从而导致电池故障并触发热失控[16]。大量燃烧事故和电池老化有关，与机械滥用相比，由电力滥用和热滥用引起的电池性能突变是导致热失控事件的主要原因。因此，电池健康状态（state of health，SOH）的准确评估是系统安全稳定运行的重要保障[17]。

电化学阻抗谱（electrochemical impedance spectroscopy，EIS）最早被用于研究线性电路网络的频率响应特性。将该特性应用到电化学系统研究中，形成了一种常用的电化学测量手段。当电化学系统受到正弦交流激励信号的扰动时，会产生相应的响应信号，通过分析这些信号可以得到系统阻抗，一系列不同频率正弦信号所产生的阻抗频谱被称为EIS。与其他电化学测量技术相比，EIS采用小信号分析，在测量过程中对系统不产生破坏作用，属于无损测量方法，稳定性高、实用性强。而且EIS可以实现从低频（1 mHz）到高频（1 MHz）的宽频范围内的电化学界面反应研究，从而获取电化学系统扩散系数和化学反应速率等物理特性[18-19]。凭借这些优点，EIS技术已经广泛应用于能源、材料、环境、生物和医学诊断等多个领域[20-24]，同时也逐渐成为分析锂离子电池性能的有力工具[25-26]。国内外学者通过处理分析实验室场景下测量得到的电池完整EIS，实现了电池健康状态与荷电状态（state of charge，SOC）评估[27-29]、电池老化机理分析[30]以及退役锂离子电池分类[31-32]等研究。然而在实验室通常使用电化学工作站、频谱分析仪等精密仪器对锂离子电池进行传统EIS测试，成本高昂且扫频测量时间长，因此无法满足现实场景对快速在线阻抗测试的迫切需求[33]。

本文提出一种基于EIS快速测试与重构技术的电池健康状态快速估计方法。首先，通过逆重复M序列设计多频电流激励，对电池进行快速阻抗谱测试；其次，采用连续小波变换实现电池阻抗谱重构，重构阻抗谱与电池EIS真值间匹配效果良好，且阻抗谱快速测试与重构过程耗时不超过4.5 min，大大缩短了测试时间；最后，根据不同衰退程度电池的重构阻抗谱在特定频率点下的阻抗幅值建立估计电池SOH的经验模型，并对模型精度进行验证与分析。

1 快速阻抗谱测试

1.1 M 序列与逆重复M 序列

最大长度序列（maximum length sequence, MLS）简称为M序列，是基本的一种伪随机二进制序列，易生成，规律性强，同时具有良好的自相关性和互相关性[34]。M序列通常采用多级反馈移位寄存器生成，如图1所示为生成M序列的n级线性移位寄存器的结构示意图。

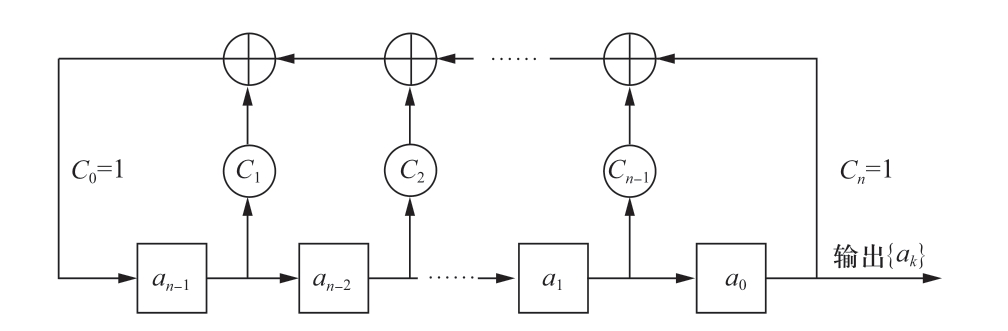
图1 n级线性移位寄存器结构示意图
Fig. 1 Schematic diagram of n-level linear shift register structure

各级寄存器状态由ai表示，值为0或1。反馈线的连接状态由ci表示，ci = 1表示反馈连接，ci = 0则表示反馈断开。最终寄存器的输出序列由所有寄存器和反馈线的状态决定。假设该n级线性移位寄存器的初始状态为a -1 a-2…a-n，经过1次移位后，状态则变为a 0a-1…a- n +1。因此，经过n次移位后，寄存器状态将更新为a n-1an-2… a0，此后再经过1次移位，移位寄存器左端新得到的输入an可以表示为

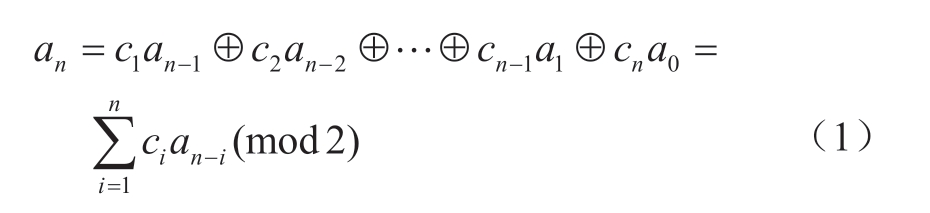
n级线性移位寄存器共有2n个状态，除去全0状态外还有2 n -1 个状态，即其所能产生的最大长度序列为2 n -1 位。因此，M序列的长度N与移位寄存器级数n之间的关系为

由上文可知，M序列是一种多频信号，通过对M序列功率谱密度分布的分析可以确定它所包含的有效频率范围。一般来说，M序列的功率谱在频率小于序列时钟频率的1/3，也就是功率谱幅值下降程度小于3 dB的区间内均匀分布。M序列的功率谱幅值随着频率的增大而快速衰减，当频率与M序列的时钟频率相等时衰减为零。随后功率谱幅值将以先增大后减小的趋势周期循环，且整体强度逐渐衰减。综上，M序列的有效带宽范围可表示为

式中：fc为M序列的时钟频率；fe为M序列测量的有效频率；n为移位寄存器的级数。

M序列作为一种二进制序列，其存在着2种状态。由于M序列具有均衡性，在1个周期内，2种状态数量基本相等。然而由式 （2） 可知，M序列的长度N总为1个奇数，因此M序列中的一种状态总比另一种状态多1个时刻。这将导致M序列含有直流成分，从而对系统造成“净扰动”。逆重复M序列的提出克服了这一缺点，是一种比M序列更为理想的伪随机序列。

逆重复M序列的生成方法与M序列同样简单。首先，在长度为N的M序列的基础上，取2N位的M序列；然后，将其隔位取逆得到的新序列即为逆重复M序列。逆重复M序列包含以下特点[35-36]。

1） 逆重复M序列的周期为原M序列的2倍。

2） 逆重复M序列包含2种出现频率相等的幅值状态，不存在直流分量。

3） 逆重复M序列具有逆对称性，即序列前后2部分呈逆对称，该特性可抑制测量过程中缓慢随机漂移对辨识结果的影响。同时由于逆重复M序列相较于M序列来说序列长度进一步扩增，因此系统的辨识精度也将得以提升。

综上所述，本文将基于逆重复M序列来设计对电池进行快速阻抗谱测试的多频电流激励信号。

1.2 基于逆重复M 序列的快速阻抗谱测试

本文选用标称容量为100 Ah的磷酸铁锂电池作为电池样品，其基本规格参数如表1所示，电池样品外观如图2所示。采用苏州清研精准汽车科技有限公司生产的T50-3W-C-J-Z充放电测试系统、150 L高低温试验箱以及由法国Bio-logic公司生产的支持10 μHz～7 MHz频率范围内电化学阻抗谱测试的VSP-300电化学工作站共同构建电池实验平台，如图3所示。

表1 电池样品基本规格参数
Table 1 Basic performance parameters of the battery sample

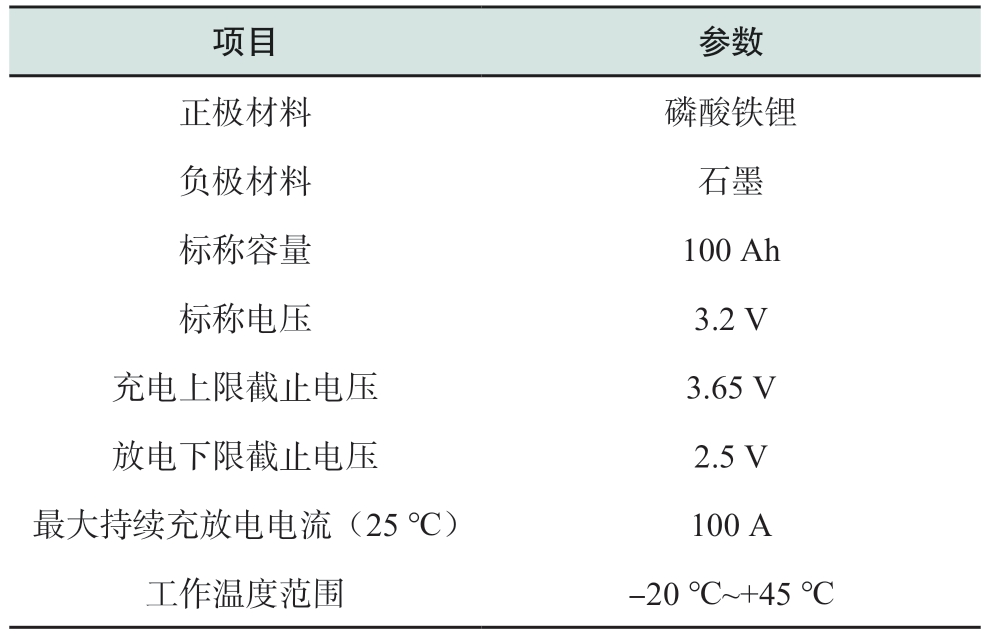
图2 电池样品外观图
Fig. 2 Appearance of the battery sample

图3 主要实验设备
Fig. 3 Main experimental equipments

通过对锂离子电池样品施加电流扰动来进行电池EIS的快速测试。在测试之前，需要选取合适的电流激励幅值，确定待测阻抗谱的目标频率范围以及对逆重复M序列的参数进行选择。下文将从以上三方面对多频电流激励信号展开设计。

1） 电流激励幅值的选取。

在通过施加电流扰动测试电池阻抗谱时，电流信号幅值不宜过高也不宜过低。幅值过高可能影响电池电量，改变电池当前的工作状态，从而增大测量误差；幅值过低将会造成阻抗谱测量的不准确。目前研究中多选用电池工作过程中最大可持续充放电电流的10%作为电流激励信号幅值[37]。本文所研究电池样品在25 ℃下的最大可持续充放电电流为1 C （100 A），因此选取幅值为10 A的电流激励来测量电池的EIS真值和开展快速阻抗谱测试。

2） 待测阻抗谱目标频率范围的确定。

在确定待测目标频率范围之前，采用恒电流法，取激励电流幅值为10 A，通过电化学工作站对电池样品进行了10 mHz～10 kHz频率下完整EIS的测量，测量结果如图4所示。对于一个典型的电池阻抗谱来说，通常由超高频段（f ＞ 1 kHz）、中高频段（1 Hz ＜ f ＜1 kHz）和低频段（f ＜ 1 Hz）组成，不同频段表征了电池在不同电化学过程中所对应的阻抗特性。其中，超高频段范围内观察到的阻抗行为可能是测量系统（连接电池和测量设备的导线）的产物，也可能源于电池和电池绕组的几何形状，该部分并不是重点关注的部分[38]。阻抗谱与实轴的高频截距对应于电池内部欧姆电阻的总和。在中高频段范围内，高频段为锂离子通过固体电解质界面（solid electrolyte interphase，SEI） 膜阻抗，中频段为电极极化阻抗，表征了电池内部的电荷转移过程。低频段是与扩散过程有关的浓差极化阻抗[39]。此外，在快速阻抗谱测量技术中，过高频率的激励信号不仅会使得电池接触点产生寄生参数从而影响测量结果，而且对信号发生器的设计提出了更高要求。由于低频处电池EIS的不稳定性较强，以至于过低频率的激励信号难以保证阻抗谱的在线测量精度[37,40]。

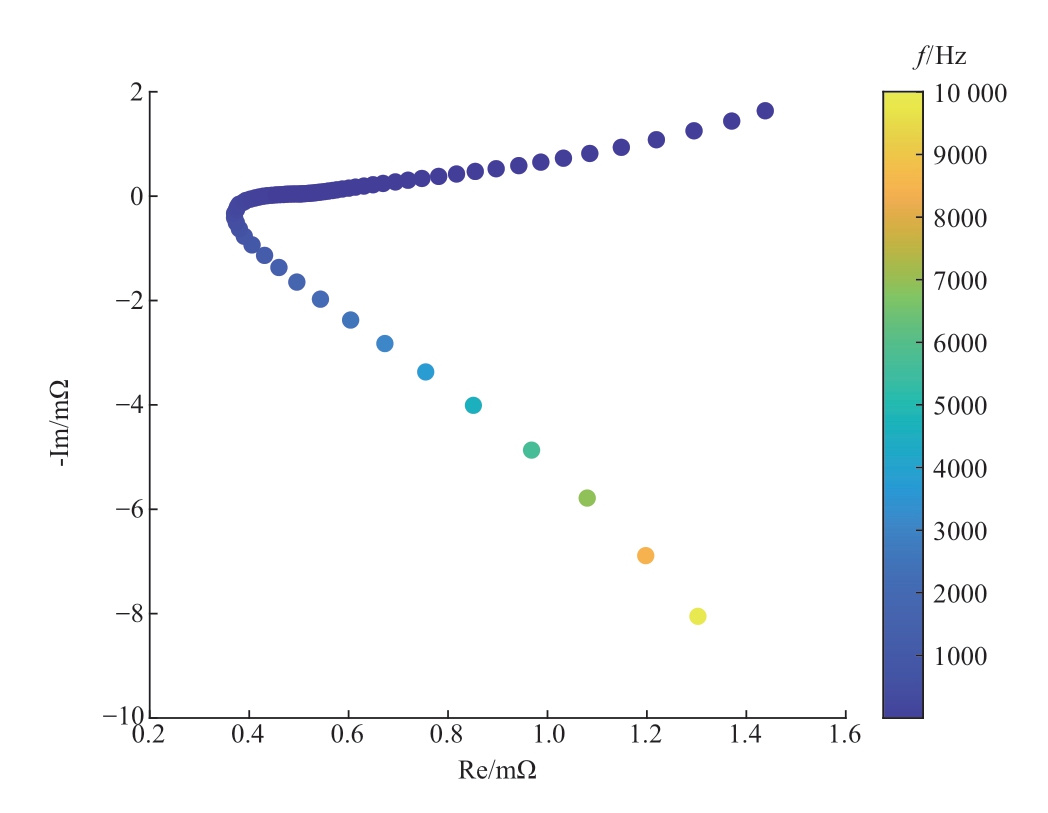
图4 10 mHz～10 kHz电池样品电化学阻抗谱
Fig. 4 Electrochemical impedance spectroscopy of 10 mHz-10 kHz for battery samples

因此，本文不再考虑电池样品EIS的超高频段以及极低频段，选择30 mHz～300 Hz作为待测试阻抗谱的目标频率范围。该范围不仅包含了电池阻抗的大部分信息，而且其测量时间也是导致传统电化学阻抗谱测试技术耗时过长的主要因素。

3） 逆重复M序列的参数选择。

由上文可知，逆重复M序列仅在特定的带宽范围内有效。此外，后续将对快速测量得到的电池电压响应与电流激励进行连续小波变换以实现电池阻抗谱重构。小波变换通过对随频率改变的“时间-频率”窗口与小波间的卷积来求取小波系数，当窗口处于信号边缘时，窗口内将会出现一部分无信号的现象。基于Matlab进行小波变换时，Matlab将会对窗口边缘处的信号强制填零来实现边界延拓，从而导致信号失真。综上，仅采用一段单独的逆重复M序列难以实现对目标频带范围30 mHz～300 Hz内电池阻抗谱的准确测试。因此，为了尽可能拓宽测量频率的有效范围，同时提高快速阻抗谱测试的精度，本文设计了三段拥有不同长度与时钟频率的逆重复M序列，分别施加到电池上，实现对高、中、低频阻抗谱的快速测试。三段逆重复M序列的具体参数如表2所示。基于其生成的电流激励信号以及获得相应的电池电压响应如图5所示。

表2 三段逆重复M序列的具体参数
Table 2 Specific parameters of the three-band inverse repeat M sequences

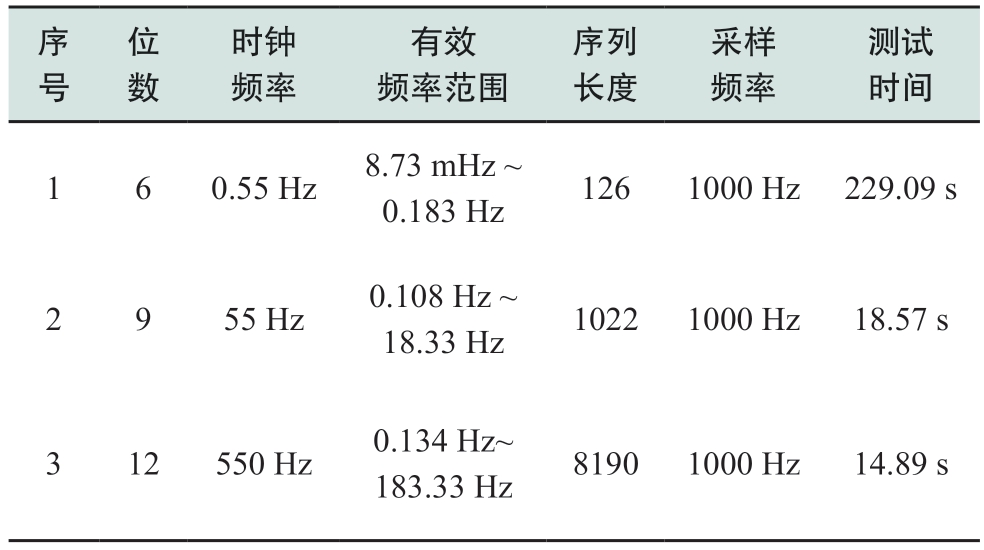
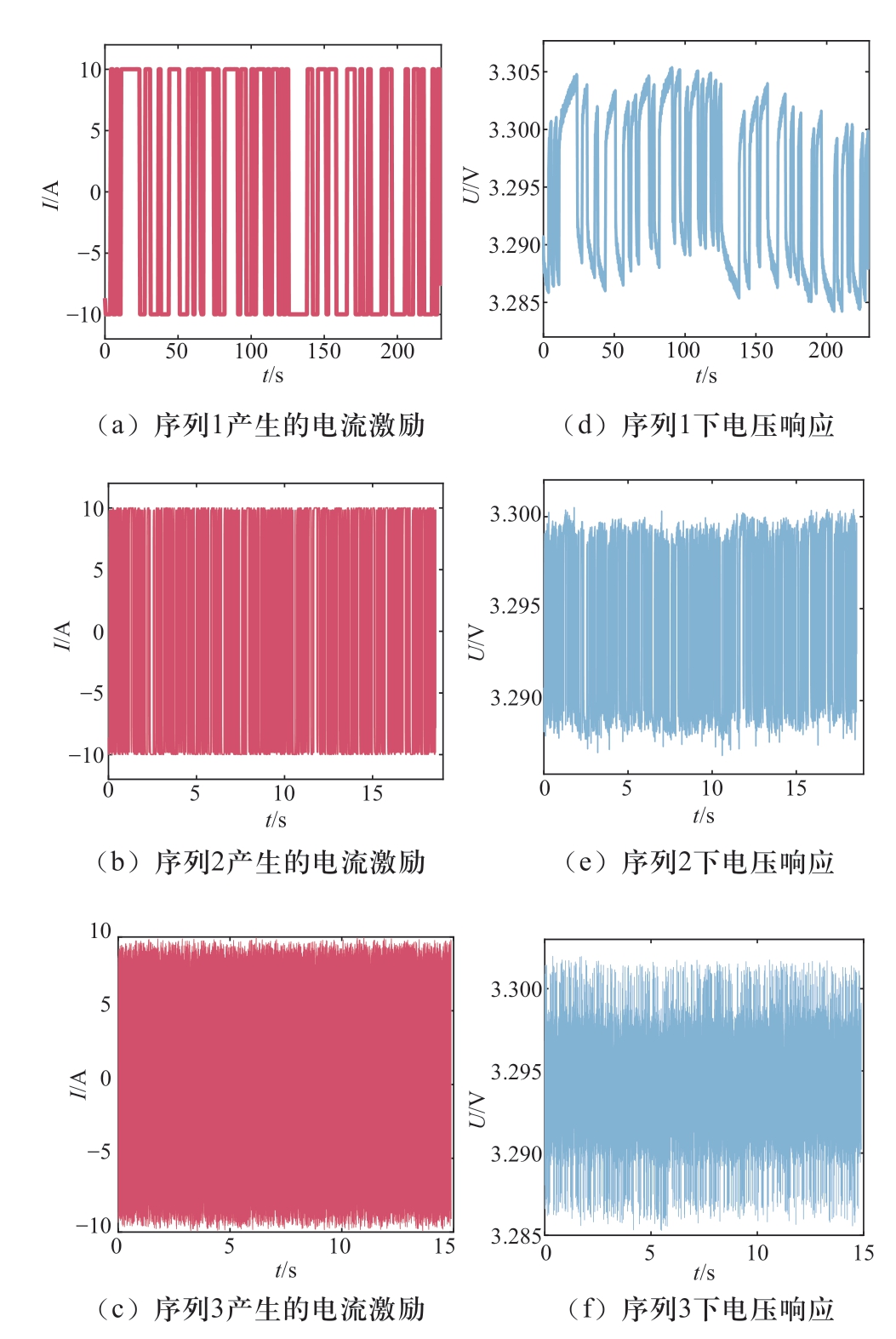
图5 基于三段逆重复M序列生成的电流激励及相应的电压响应
Fig. 5 Current excitation and corresponding voltage response based on three-band inverse repetitive M sequences

其中，对电池样品高、中、低频段阻抗谱进行测试的测试时间分别为14.89 s、18.58 s和229.09 s，实现目标频率范围30 mHz～300 Hz电池阻抗谱测试的总耗时为262.56 s，小于4.5 min。相比之下，在实验室采用电化学工作站对所研究电池样品目标频率范围内EIS进行测试时，测试时间长达30 min。由此可见，本文采用基于逆重复M序列设计的电流激励信号分段进行电池阻抗谱的快速测试方法，大大缩短了阻抗谱的测试时间。

2 基于Morse复小波变换的阻抗谱重构

2.1 连续小波变换

小波变换（wavelet transform，WT）是相较于短时傅里叶变换更为优越的一种时频分析方法，它继承了短时傅里叶变换的局部化思想，同时克服了短时傅里叶变换时频分辨率无法自适应的缺点。小波变换和傅里叶变换本质相似，其基本思想是将傅里叶变换中无限长的三角基函数更换为有限长会衰减的小波基函数。通过小波基的伸缩和平移，可以对信号进行多尺度分析，最终实现对信号高频部分的时间细分以及对信号低频部分的频率细分。小波变换又分为连续小波变换（continuous wavelet transform，CWT）与离散小波变换（discrete wavelet transform，DWT）。其中，CWT在所有可能的伸缩和平移上操作，多应用于信号的时频分析和成分滤波；而DWT采用所有伸缩和平移值的特定子集，主要应用于信号和图像的去噪、压缩。一般来说，对于连续信号采用连续小波变换，对于离散信号则采用离散小波变换。本文需要处理的施加于电池的电流激励与获得的电压响应都是时域上的连续变换信号，因此采用CWT对二者进行时频分析，从而获取电池在不同频率下的阻抗信息。

在CWT中，任何随时间连续变化的信号f(t)都可以用一组小波函数ψ( t) 来表示：

在小波变换中，有许多可供选择的母小波类型，每个母小波具有不同的特性。本文目标为分析电池的阻抗数据，因此选用复小波。在CWT中，常见的复小波包括Morlet小波、Bump小波、Morse小波和Lognormal小波。其中，Morlet小波已被广泛应用于电池阻抗谱重构技术[41-42]。Nusev等[43]分别从时间分辨率、频率分辨率以及两者的联合分辨率对Morlet小波和Morse小波进行了比较，结果表明两者时间分辨率相似，但Morlet小波在信号中心频率过低时会出现平台。相比之下，Morse小波即使在超低频下也能保持其分析特性。因此，基于对电池重构阻抗谱低频处精度的考虑，本文在后续分析中皆选用Morse小波。Morse小波是一组具有双参数的小波基，目的是为了获取最大化时频定位算子的特征值。Morse小波在频域中的一般形式如下：

式中：U( )ω 是单位阶跃；aP,γ 是归一化常数；P2是时间-带宽积；γ 表征Morse小波的对称性。通过调整Morse小波的时间带宽积和对称参数，可以获得具有不同性质和行为的解析小波。时间-带宽积还可以表示为βγ，β 为衰减参数，由β 和γ 参数化的Morse小波的方程为

对通过电池快速阻抗谱测试获得的电池电流激励信号i(t)和电压响应信号u(t)分别进行CWT，将产生一组复数小波系数：

式中：Wx (t ,f )是时间t和频率 f的函数，表示信号x(t)的小波。阻抗是电压和电流小波系数的比值：

对于一个逆重复M序列，其在一定尺度上的小波系数可视为一个高斯复随机分布变量[44]，也就是说变换得到阻抗的实、虚部可看作为正态分布，该正态分布期望的极大似然估计值可近似为某一频率下的电池阻抗[45]。

2.2 阻抗谱重构及验证分析

在通过基于逆重复M序列设计的电流激励信号对电池单体样品进行目标频率范围内快速阻抗谱测试的基础上，采用以Morse小波作为母小波的CWT对电池电流激励与电压响应进行时频分析，从而获得二者的小波系数。最后，通过目标频率范围内阻抗时间序列的最大似然估计得到对应频率点下电池的阻抗信息，共同实现电池的快速阻抗谱测试与重构。以50%SOC的新鲜电池样品为例，图6 （a）—（c） 所示分别为在设计的三段逆重复M序列下，重构阻抗谱与电池EIS真值间的匹配结果，图7所示为三段重构阻抗谱的有效部分拼接结果。

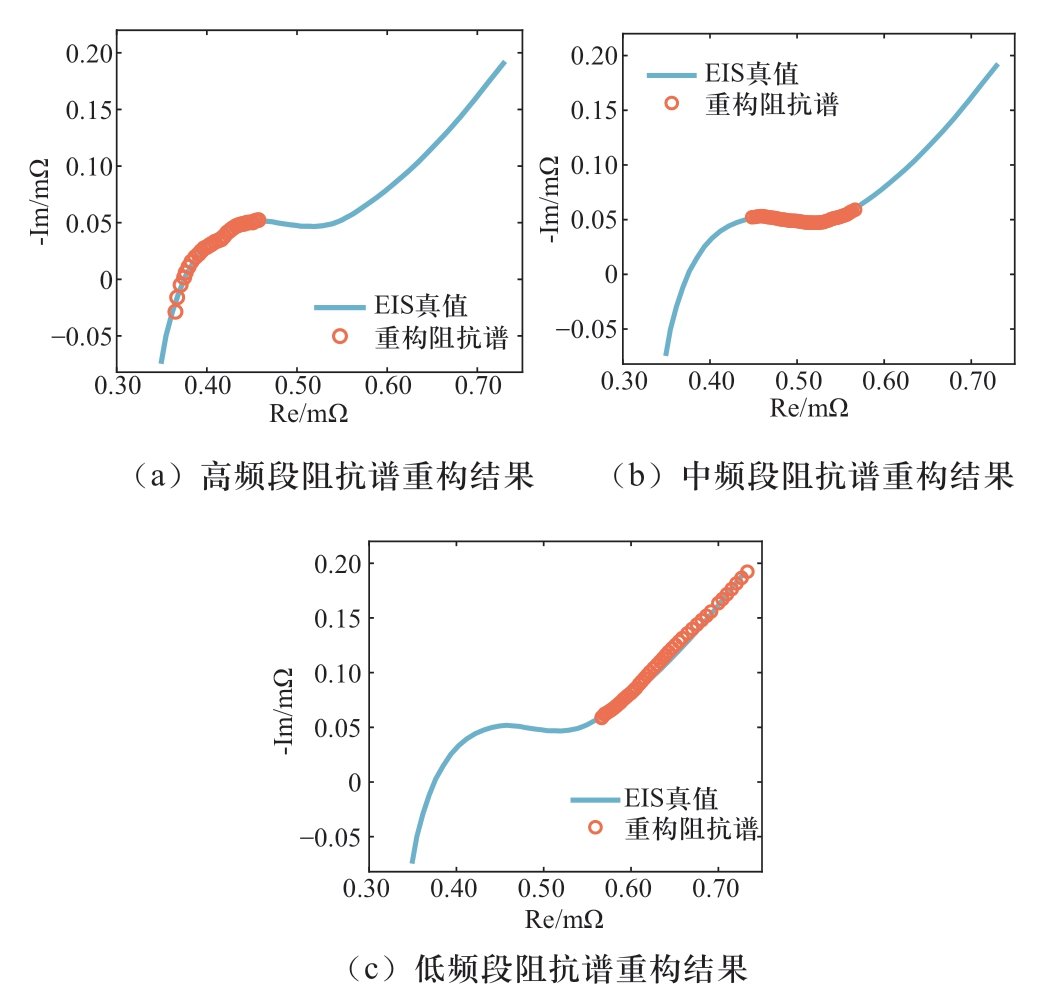
图6 三段重构阻抗谱与电池EIS真值对比结果
Fig. 6 Comparison results between the three-band reconstructed impedance spectroscopy and the true value of the battery EIS

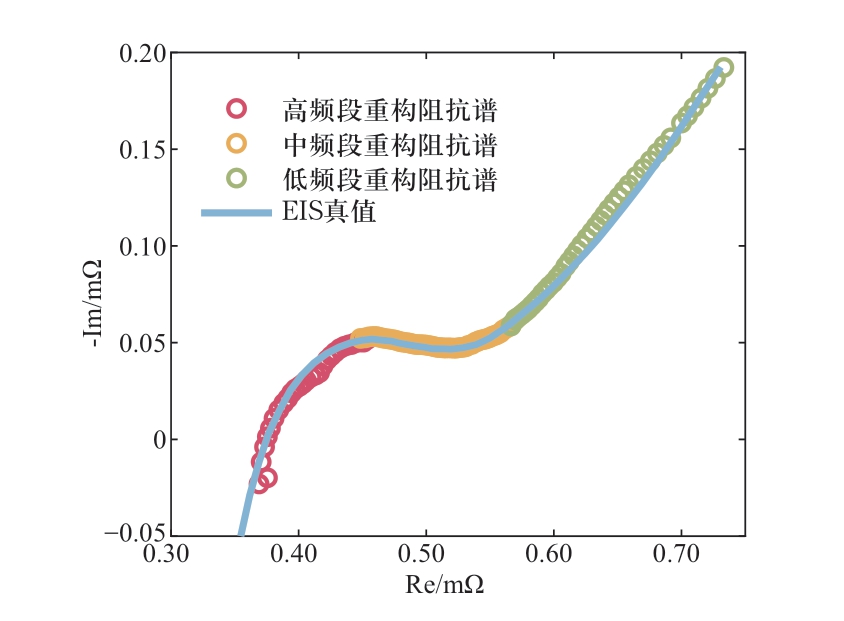
图7 三段重构阻抗谱的有效部分拼接结果
Fig. 7 The result of the effective partial splicing of the three-band reconstruction impedance spectroscopy

可以明显观察到，在待测目标频率范围内，不同频段下经快速测试与重构的电池阻抗谱与EIS真值间匹配效果良好。除此之外，基于本文所设计的多频电流激励信号对电池进行快速阻抗谱测试，耗时小于4.5 min，大大缩短了测试时长。基于对精度和耗时的共同考虑，本文所提出的电池阻抗谱快速测试及重构方法更符合现实应用场景下对阻抗谱在线实时测量的需求，对工程实际具有一定的指导意义。

3 电池SOH估计经验模型建立及验证

在对锂离子电池阻抗谱快速测试与重构的基础上，本章通过特定频率点下电池重构阻抗谱包含的阻抗信息，建立基于多元线性回归方程的电池健康状态估计经验模型，从而实现电池SOH的快速评估。

锂离子电池在相同SOH的不同SOC点下电化学阻抗谱的整体趋势保持一致，因此为了实现对电池健康状态的定量分析，本文在相同SOC点对不同老化状态下电池进行快速阻抗谱测试与重构。图8所示为经快速阻抗谱测试与重构得到的不同老化状态电池样品在50%SOC时的重构阻抗谱。

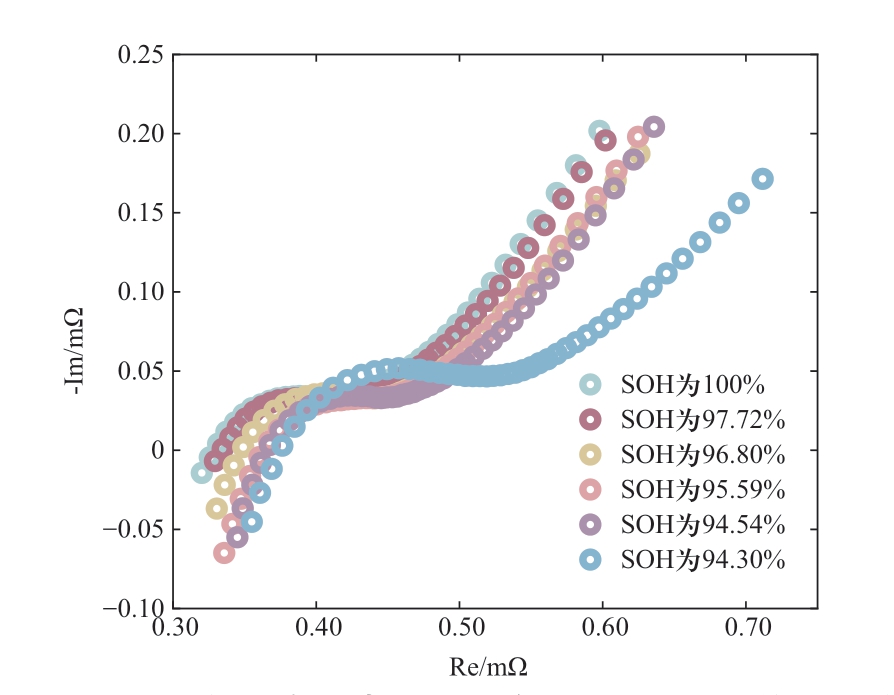
图8 不同老化状态下电池样品在50%SOC下重构阻抗谱
Fig. 8 Reconstructed impedance spectroscopy of battery samples at 50% SOC for different aging states

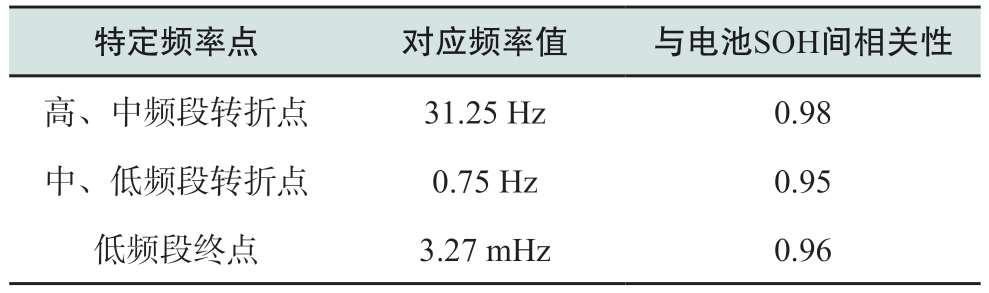
可以明显观察到阻抗谱随电池老化发生偏移，在此基础上，选取了3个特殊频率点，即重构阻抗谱的低频段终点以及高、中频段之间和中、低频段之间的切换点。通过计算重构阻抗谱在3个特定频率点下的阻抗幅值与电池健康状态间的皮尔逊相关性系数，对其进行相关性分析，结果如表3所示。从表3可以得知，重构阻抗谱在所选取的3个特定频率点下的阻抗幅值与电池健康状态高度相关，皮尔逊相关性系数均在0.95以上，因此可以选用特定频率点下的阻抗幅值进行电池SOH估计。

表3 重构阻抗谱特定频率点阻抗幅值与电池SOH间相关性
Table 3 Correlation between the impedance amplitude at a specific frequency point of the reconstructed impedance spectroscopy and the SOH of the battery

为确定各阻抗幅值与电池SOH间的关系，建立二者间的多元线性回归方程，如式 （9） 所示：

式中： 为电池SOH，作为方程的因变量；x1、x2和x3分别对应重构阻抗谱在高、中频段间和中、低频段之间的切换点以及低频段终点的阻抗幅值；a1、a2、a3、b为自变量所对应的系数和常数项。

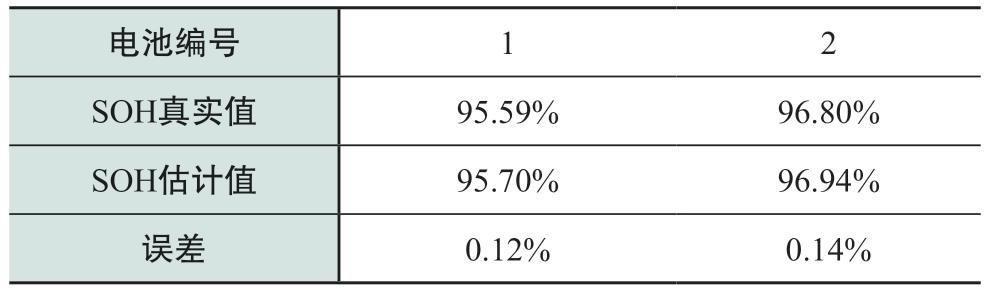
本文采用6只不同健康状态电池样品的重构阻抗谱数据对线性回归方程进行建立与验证，电池单体样品当前健康状态如表4所示，其中衰退程度最大电池已进行300圈循环老化实验，当前SOH为94.30%。采用4只不同老化状态电池建立多元线性回归方程，另外2只电池用以验证该方程估计SOH的精度。所建立的多元线性回归方程各系数如表5所示。如式 （10） 所示，计算SOH估计值与真实值间的相对误差。将自变量和系数值代入方程，可得结果与误差如表6所示，相对误差不超过0.2%，估计效果良好。

表4 模型建立与验证所用电池单体样品的健康状态
Table 4 SOH of the battery cell samples used for modeling and validation

表5 多元线性回归方程式系数
Table 5 Coefficients of multiple linear regression equation

表6 SOH估计值及误差
Table 6 SOH estimation value and error

4 结论

本文基于对锂离子电池阻抗谱的快速测试与重构，根据不同老化状态电池在高、中、低频段转换时刻特定频率下的重构阻抗幅值建立电池SOH估计的经验模型，实现了锂离子电池SOH的快速准确评估，所得结论如下。

1） 基于逆重复M序列设计了三段电流激励信号对不同频段下阻抗谱进行测试，整个过程耗时小于4.5 min，大大缩短了测试时长。

2） 在快速阻抗谱测试的基础上，采用连续小波变换对电池电流激励和电压响应进行时频分析，从而实现了电池阻抗谱重构。经验证，重构阻抗谱与电池EIS真值间匹配效果良好。

3）通过不同老化状态下电池在高、中、低频段转换时刻特定频率下的重构阻抗幅值建立电池SOH估计经验模型。结果表明，该SOH快速评估方法误差小于0.2%，拥有较高的估计精度。

参考文献

[1] 刘泽洪，周原冰，金晨. 支撑新能源基地电力外送的电源组合优化配置策略研究[J]. 全球能源互联网，2023，6(2)：101-112.LIU Zehong, ZHOU Yuanbing, JIN Chen. Optimization strategy study on installation mix of renewable energy power base for supporting outbound delivery[J]. Journal of Global Energy Interconnection, 2023, 6(2): 101-112 (in Chinese).

[2] 汪万发，张彦著. 碳中和趋势下城市参与全球气候治理探析[J]. 全球能源互联网，2022，5(1)：97-104.WANG Wanfa, ZHANG Yanzhu. Analysis of cities participating in global climate governance in the trend of carbon neutrality[J]. Journal of Global Energy Interconnection,2022, 5(1): 97-104 (in Chinese).

[3] 李明. 适应能源电力新形势的“供电+能效服务” 模式创新发展研究[J]. 电力需求侧管理，2022，24(1)：2-6.LI Ming. Study on innovation and development of “power +energy efficiency service” mode adapting to new energy and power situation[J]. Power Demand Side Management, 2022,24(1): 2-6 (in Chinese).

[4] 王睿，孙秋野，胡伟，等. 面向“碳达峰、碳中和” 的新型电力系统的潮流计算[J]. 全球能源互联网，2022，5(5)：439-446.WANG Rui, SUN Qiuye, HU Wei, et al. Power flow calculation of new power system for carbon peaking and carbon neutralization[J]. Journal of Global Energy Interconnection,2022, 5(5): 439-446 (in Chinese).

[5] 张志行，韩雪冰，冯旭宁，等. 面向不同电流工况的锂离子电池改进EECM研究[J]. 电力工程技术，2023，42(4)：2-12.ZHANG Zhihang, HAN Xuebing, FENG Xuning, et al.Improved EECM for lithium-ion batteries under different current conditions[J]. Electric Power Engineering Technology,2023, 42(4): 2-12 (in Chinese).

[6] 王开让，刘辉，邹乃鹏，等. 并联锂离子电池组建模及不均衡电流分析[J]. 全球能源互联网，2023，6(2)：179-185.WANG Kairang, LIU Hui, ZOU Naipeng, et al. Modeling and unbalanced current analysis of parallel lithium-ion battery packs[J]. Journal of Global Energy Interconnection, 2023, 6(2):179-185 (in Chinese).

[7] 邓子豪，夏向阳，张嘉诚. 磷酸铁锂电池优化多因子状态在线评估方法[J]. 电网与清洁能源，2022，38(3)：90-96.DENG Zihao, XIA Xiangyang, ZHANG Jiacheng. An optimized multi-factor online assessment method of SOH for LiFePO4 batteries[J]. Power System and Clean Energy, 2022,38(3): 90-96 (in Chinese).

[8] 岳家辉，夏向阳，吕崇耿，等. 计及健康特征信息量的锂离子电池健康状态与剩余寿命预测研究[J]. 电力系统保护与控制，2023，51(22)：74-87.YUE Jiahui, XIA Xiangyang, LÜ Chonggeng, et al. Research on the prediction of state of health and remaining useful life of lithium-ion batteries considering the amount of health factors information[J]. Power System Protection and Control, 2023,51(22): 74-87 (in Chinese).

[9] 邹红波，柴延辉，杨钦贺，等. 基于混合ISSA-LSTM的锂离子电池剩余使用寿命预测[J]. 电力系统保护与控制，2023，51(19)：21-31.ZOU Hongbo, CHAI Yanhui, YANG Qinhe, et al. Remaining useful life prediction of lithium-ion batteries based on hybrid ISSA-LSTM[J]. Power System Protection and Control, 2023,51(19): 21-31 (in Chinese).

[10] 王鹏博，郑俊超. 锂离子电池的发展现状及展望[J]. 自然杂志，2017，39(4)：283-289.WANG Pengbo, ZHENG Junchao. The present situation and expectation of lithium-ion battery[J]. Chinese Journal of Nature, 2017, 39(4): 283-289 (in Chinese).

[11] 2022年中国及31省市动力锂电池行业政策汇总及解读[EB/OL]. (2022-9-26)[2023-12-10]. https://new.qq.com/rain/a/20220926A06B7I00.

[12] FENG F, HU X S, LIU K L, et al. A practical and comprehensive evaluation method for series-connected battery pack models[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 391-416.

[13] KONG F H, LIANG X, YI L L, et al. Multi-electron reactions for the synthesis of a vanadium-based amorphous material as lithium-ion battery cathode with high specific capacity[J].Energy, 2021, 219: 119513.

[14] 顾菊平，蒋凌，张新松，等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报，2023，38(19)：5330-5342.GU Juping, JIANG Ling, ZHANG Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342 (in Chinese).

[15] 薛太林，张超，闫来清，等. 基于WOA-BP神经网络的锂离子电池健康状态估算[J]. 山东电力技术，2022，49(10)：16-22.XUE Tailin, ZHANG Chao, YAN Laiqing, et al. Health state estimation of lithium-ion battery based on WOA-BP neural network[J]. Shandong Electric Power, 2022, 49(10): 16-22 (in Chinese).

[16] FENG X N, PAN Y, HE X M, et al. Detecting the internal short circuit in large-format lithium-ion battery using modelbased fault-diagnosis algorithm[J]. Journal of Energy Storage,2018, 18: 26-39.

[17] 姜研. 梯次利用锂离子电池组全生命周期状态评估技术研究[D]. 北京：北京交通大学，2021.

[18] 张连德. 基于电化学阻抗谱的三元锂离子电池状态估计研究[D]. 长春：吉林大学，2018.

[19] 冷晓伟，戴作强，郑莉莉，等. 锂离子电池电化学阻抗谱研究综述[J]. 电源技术，2018，42(11)：1749-1752.LENG Xiaowei, DAI Zuoqiang, ZHENG Lili, et al. Review on electrochemical impedance spectroscopy of lithium-ion batteries[J]. Chinese Journal of Power Sources, 2018, 42(11):1749-1752 (in Chinese).

[20] ARIYOSHI K, MINESHIGE A, TAKENO M, et al. Electrochemical impedance spectroscopy part 2:applications[J]. Electrochemistry, 2022, 90(10): 102008.

[21] PARK J, SONG H, CHOI H. Estimation of water-tocement ratio in cementitious materials using electrochemical impedance spectroscopy and artificial neural networks[J].Construction and Building Materials, 2022, 350: 128843.

[22] ENCINAS-SÁNCHEZ V, DE MIGUEL M T, LASANTA M I, et al. Electrochemical impedance spectroscopy (EIS):an efficient technique for monitoring corrosion processes in molten salt environments in CSP applications[J]. Solar Energy Materials and Solar Cells, 2019, 191: 157-163.

[23] LI X, QIN Z, FU H, et al. Enhancing the performance of paperbased electrochemical impedance spectroscopy nanobiosensors:an experimental approach[J]. Biosensors and Bioelectronics,2021, 177: 112672.

[24] WANG T Y, LIU Q, REN Y, et al. A pan-cancer transcriptome analysis of exitron splicing identifies novel cancer driver genes and neoepitopes[J]. Molecular Cell, 2021, 81(10): 2246-2260.e12.

[25] 张闯，王泽山，刘素贞，等. 基于电化学阻抗谱的锂离子电池过放电诱发内短路的检测方法[J]. 电工技术学报，2023，38(23)：6279-6291.ZHANG Chuang, WANG Zeshan, LIU Suzhen, et al. Detection method of overdischarge-induced internal short circuit in lithium-ion batteries based on electrochemical impedance spectroscopy[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6279-6291 (in Chinese).

[26] 孙丙香，王家驹，苏晓佳，等. 基于阶梯波的锂离子电池电化学阻抗谱低频段在线辨识方法[J]. 电工技术学报，2023，38(11)：3064-3072.SUN Bingxiang, WANG Jiaju, SU Xiaojia, et al. Study on online identification method of low frequency electrochemical impedance spectroscopy for lithium-ion battery based on step wave[J]. Transactions of China Electrotechnical Society, 2023,38(11): 3064-3072 (in Chinese).

[27] MESSING M, SHOA T, HABIBI S. Estimating battery state of health using electrochemical impedance spectroscopy and the relaxation effect[J]. Journal of Energy Storage, 2021, 43:103210.

[28] JIANG B, ZHU J G, WANG X Y, et al. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries[J]. Applied Energy, 2022, 322: 119502.

[29] BABAEIYAZDI I, REZAEI-ZARE A, SHOKRZADEH S.State of charge prediction of EV Li-ion batteries using EIS: a machine learning approach[J]. Energy, 2021, 223: 120116.

[30] ZHANG Q, WANG D F, SCHALTZ E, et al. Degradation mechanism analysis and state-of-health estimation for lithiumion batteries based on distribution of relaxation times[J].Journal of Energy Storage, 2022, 55: 105386.

[31] 来鑫，陈权威，邓聪，等. 一种基于电化学阻抗谱的大规模退役锂离子电池的软聚类方法[J]. 电工技术学报，2022，37(23)：6054-6064.LAI Xin, CHEN Quanwei, DENG Cong, et al. A soft clustering method for the large-scale retired lithium-ion batteries based on electrochemical impedance spectroscopy[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6054-6064 (in Chinese).

[32] 骆凡，黄海宏，王海欣. 基于短时脉冲放电与电化学阻抗谱的退役动力电池快速分选与重组方法[J]. 仪器仪表学报，2022，43(1)：229-238.LUO Fan, HUANG Haihong, WANG Haixin. A fast screening and recombinant method based on short-time pulse discharge and electrochemical impedance spectroscopy for decommissioned power batteries[J]. Chinese Journal of Scientific Instrument, 2022, 43(1): 229-238 (in Chinese).

[33] LYU C, LIU H Y, LUO W L, et al. A fast time domain measuring technique of electrochemical impedance spectroscopy based on FFT[C]//2018 Prognostics and System Health Management Conference (PHM-Chongqing).Chongqing, China. IEEE, 2018: 450-455.

[34] 王会华，李宝平. m序列发生器的设计与实现[J]. 北京电子科技学院学报，2007，15(2)：58-61.WANG Huihua, LI Baoping. Design and realize of m sequence generator[J]. Journal of Beijing Electronic Science and Technology Institute, 2007, 15(2): 58-61 (in Chinese).

[35] 钟延炯. 逆重复m序列及系统辨识[J]. 自动化学报，1979，5(2)：107-115.ZHONG Y J. Inverse-repeat m sequence and system identification[J]. Acta Automatica Sinica, 1979, 5(2): 107-115(in Chinese).

[36] 黄金峰，张合新，李旭渊. 逆重复M序列相关辨识法的一种改进[J]. 弹箭与制导学报，2011，31(3)：227-231.HUANG Jinfeng, ZHANG Hexin, LI Xuyuan. The improvement of correlated identification based on invertedrepeated M-sequence signal[J]. Journal of Projectiles, Rockets,Missiles and Guidance, 2011, 31(3): 227-231 (in Chinese).

[37] YUAN X, WANG H, COLINSUN J, et al. AC impedance technique in PEM fuel cell diagnosis—a review[J].International Journal of Hydrogen Energy, 2007, 32(17): 4365-4380.

[38] MEDDINGS N, HEINRICH M, OVERNEY F, et al.Application of electrochemical impedance spectroscopy to commercial Li-ion cells: a review[J]. Journal of Power Sources,2020, 480: 228742.

[39] 魏刚. 基于阻抗谱的锂离子电池快速状态评估系统设计[D].哈尔滨：哈尔滨工业大学，2020.

[40] FOUQUET N, DOULET C, NOUILLANT C, et al. Model based PEM fuel cell state-of-health monitoring via AC impedance measurements[J]. Journal of Power Sources, 2006,159(2): 905-913.

[41] 李伟恒. 快速阻抗谱测试及其在电动汽车中的应用研究[D].武汉：湖北大学，2019.

[42] 赵云飞，徐俊，王海涛，等. 采用Morlet小波的锂电池相对健康状态估计[J]. 西安交通大学学报，2019，53(12)：97-103.ZHAO Yunfei, XU Jun, WANG Haitao, et al. An estimation method of relative state-of-health for lithium-ion batteries using Morlet wavelet[J]. Journal of Xi’an Jiaotong University,2019, 53(12): 97-103 (in Chinese).

[43] NUSEV G, JURIČIĆ Đ, GABERŠČEK M, et al. Fast impedance measurement of Li-ion battery using discrete random binary excitation and wavelet transform[J]. IEEE Access, 2021, 9: 46152-46165.

[44] DEBENJAK A, PETROVČIČ J, BOŠKOSKI P, et al. Fuel cell condition monitoring system based on interconnected DCDC converter and voltage monitor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 5293-5305.

[45] 卢华歆. 基于快速电化学阻抗谱测量的在线质子交换膜燃料电池故障诊断[D]. 杭州：浙江大学，2020.

收稿日期：2024-01-15；修回日期：2024-02-18。

作者简介：

                                                        

侯林涛

侯林涛（1998），女，博士研究生，研究方向为锂离子电池状态评估和寿命预测，E-mail：23111464@bjtu.edu.cn。

张彩萍（1982），女，教授，博士生导师，主要研究方向为电动汽车动力电池和储能电池在电力系统中的应用。通信作者，E-mail：zhangcaiping@bjtu.edu.cn。

（责任编辑 李锡）