0 引言

2015年“新电改”实施以来，中国已经初步建成了统一市场、区域-省级电网两级运作的市场模式，建立了体系健全、规则完善的中长期交易运行机制，推进了以南方（以广东起步）为代表的首批8个省级电力现货试点和第二批5个省级现货试点，南方区域现货市场也在2022年7月正式试运行，中国电力市场改革已经步入深水区。西南地区作为中国水电富集地区，水电资源约占全国的70%，已建成澜沧江、金沙江、乌江、南盘江-红水河等特大流域梯级水电站。这些流域干流梯级水电站很多需要跨省跨区送电至中国南部沿海和华东等高负荷地区，涉及单一水电站不同机组、上下游梯级不同电站送电不同省份的复杂并网关系，面临差异特性的电力市场和交易品种，需要在多个省份、多个时间尺度、多个交易品种间进行合理的电量配置，实现电力资源的高效消纳[1-5]。

电力市场环境下，如何确保交易电量顺利履约直接关系到西南水电跨省消纳[6-10]。特别是对于水电站，由于来水不确定性，以及复杂调度运行边界限制，可能出现中长期交易电量未完全执行或交易电量没有成交但电厂超发等现象，如何合理分解水电交易电量，保障交易合同顺利执行是目前水电参与电力市场交易的重要生产业务和关键问题，其问题难点体现在以下方面。

一是多个受电省份的电量比例、调峰需求均不相同，体现在各省之间的总受电量以及不同品种电量的分配比例均需要分别控制，而且不同省份的96点负荷曲线差异较大，负荷峰、平、谷分段方式不同，电网峰谷比要求不同，多电网调峰响应困难[11-13]。二是电量和电力分配面临复杂的时空耦合限制约束，多个品种的电量需要考虑总的分配比例，且所有品种电量的时序出力分配过程需要满足逐时段总发电能力平衡要求。三是需要上、中、下旬分别考虑，确定各旬各日的电量分配，以及逐日、逐小时、各个省份、各个品种电量的分解过程；此外还涉及电站调度运行的开机、最小技术出力、出力平稳性等复杂约束条件，时空耦合强，建模与求解难度大，是非常复杂的高维非线性优化问题[14-17]。

目前，有关交易电量曲线分解的研究主要集中于发电侧和电网侧两个不同角度。从发电侧来看，一般考虑梯级水电站各项短期运行约束、日电量合同分解曲线相关约束，构建交易电量分解综合收益最大模型[18-19]；从电网侧来看，一般从电网日前计划编制实际需求出发，兼顾购电经济性、节能降耗、竞价与非竞价机组调度公平性目标，考虑水电、火电及系统运行复杂约束，构建优化模型[20]。在实际运行中，通常采用调度运行经验进行交易电量的分解[21-25]，并侧重考虑弃水及交易电量的执行公平性，一般通过汛期、枯期两类典型情况构建适合的分解策略。在枯期，大多数水电站来水较少，梯级水电站群库容补偿空间较大，应优先考虑尽可能少弃水或不弃水，进而再考虑交易电量公平执行；在汛期，大多数水电站面临弃水问题，可优先考虑交易电量执行的公平性。

本文依托水电站实际生产需求，构建了适合跨省、跨区送电巨型水电站的月度合同电量曲线分解模型[26-27]，考虑保量保价、保量竞价、市场化三类品种电价差异，提出多省多品种发电收益总和最大的二次规划目标，考虑电网调峰需求、逐时电力平衡约束、电量平衡约束、省/旬/品种的电量上下限约束、出力波动控制、出力爬坡等复杂约束，采用混合整数线性规划方法实现模型高效求解。以金沙江下游溪洛渡右岸水电站为例，通过枯期、汛期两个不同的应用场景和实际数据验证了模型的有效性和实用性。

1 数学模型及求解

1.1 目标函数

中长期电量曲线分解是在满足电站调度运行边界条件、不同电网电量和调峰需求条件下，以电站效益为目标[19,28]，通过优化分省、分旬、分品种的分时出力曲线，尽可能最大化电量收益。本文考虑目前跨省跨区送电水电站常用的保量保价、保量竞价、市场化三个电量品种，构建了收益目标函数：

式中：nk,1,d,t、nk,2,d,t、nk,3,d,t为自变量；ak,t为省份k市场化电量在t小时相对于基准价的上浮或下浮系数；Pk,1、Pk,2、Pk,3分别为送省份k的保量保价电量的价格、保量竞价电量的价格、市场化电量的基准价。

1.2 约束条件

1.2.1 电力约束

1）电力分配约束。

式中：Nxmax为各旬最大出力；ak,v,d为省份k品种v日期d的分日系数；bk,v,x,d为省份k品种v旬x时间t的分时系数，此系数含义为各时段分配出力所占省份k品种v旬x最大出力的比例；nk,v,d,t为省份k品种v日期d时间t的出力。

2）出力爬坡约束。

式中：nud为电站爬坡与降出力最大值限制。

1.2.2 电量约束

1）电量比例约束。

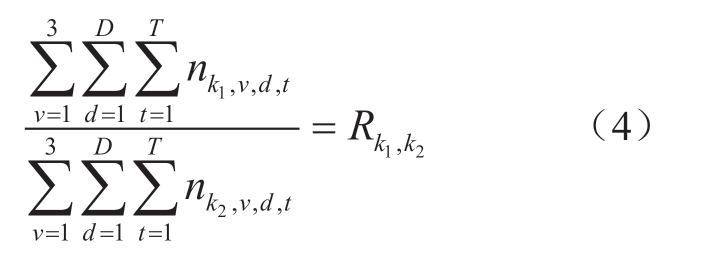
式中：Rk1,k2为k1省与k2省电量比例要求。可通过式 （4）对任意省份间电量比例进行描述。

2）总电量平衡约束。

式中：Q为当月计划外送电量。

3）分省分品种电量平衡约束。

式中：Ek,v为各省、品种签约电量。

4）某省、旬、品种的电量上下限约束。

式中：分别为各省、品种、旬签约电量上、下限。

1.2.3 分配系数约束

1）工作日日削减系数必须为最大。

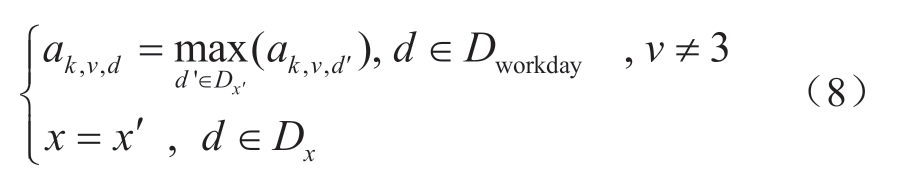
2）非工作日日削减系数约束。

式中：β为非工作日日折减系数。

3）工作日要将最大负荷全部分配，非工作日要分配指定比例的最大负荷。

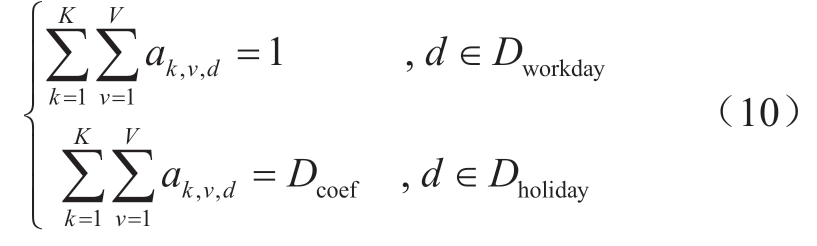
式中：β为非工作日日折减系数。

4）分时比例约束。

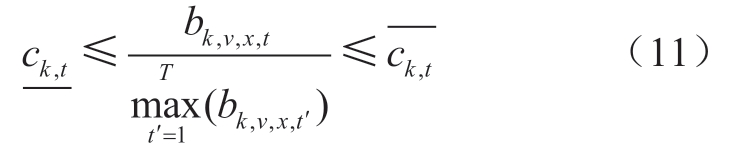
式中：分别为分时系数的上下限。

5）分时出力波动限制。

式中：∆=1,2,…,tmin，tmin为i电站出力最小间隔时段数。

6）市场化出力在峰平谷各时段内部均分。

式中：h为小时编号；p为峰平谷标识。h与p有对应关系。

1.2.4 模型系数与申报单系数转化

1）申报单分日系数。

2）申报单分时系数。

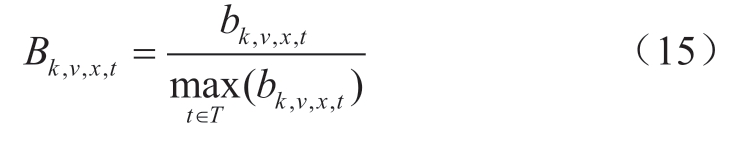
1.3 模型求解

从数学上讲，上述交易电量曲线分解模型是非常复杂的大规模非线性优化问题，以单月为电量分配周期，以小时为曲线分解尺度，涉及4456个连续变量、286个0-1变量，5408个非线性约束、1063个线性约束，维数高、非线性约束多，求解难度大。为实现模型高效求解，需要对复杂约束进行等效处理，本节提出分日、分时曲线分解系数处理策略。

1）分日系数处理策略。

由于分日系数约束存在最大值函数，故引入中间变量DMk,v,x代表分日系数ak,v,d在当旬的最大值。

确定省份和品种的分日系数在工作日时均为该省份该品种当旬最大值，在非工作日时与该省份该品种当旬最大值有一定比例限制。

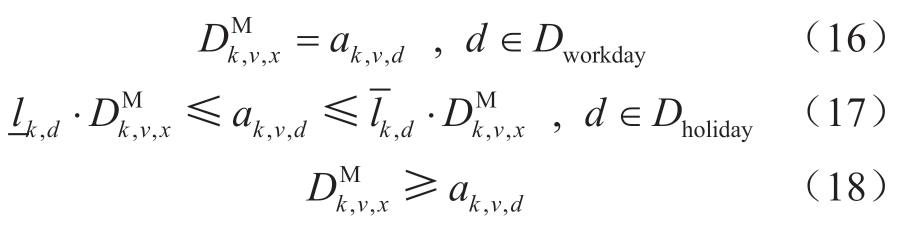
对于所有省份和品种的日出力，在工作日各省各品种出力和等于当旬最大出力，在非工作日要有一定比例范围限制。

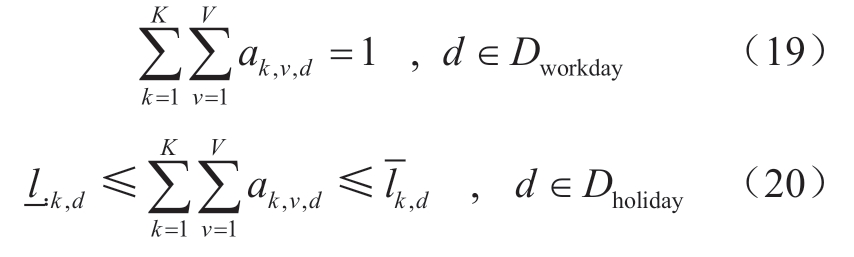
2）分时系数处理策略。

分时系数带有最大值函数，故引入中间变量HMk,v,x和λk,v,x,t，以便于模型求解。

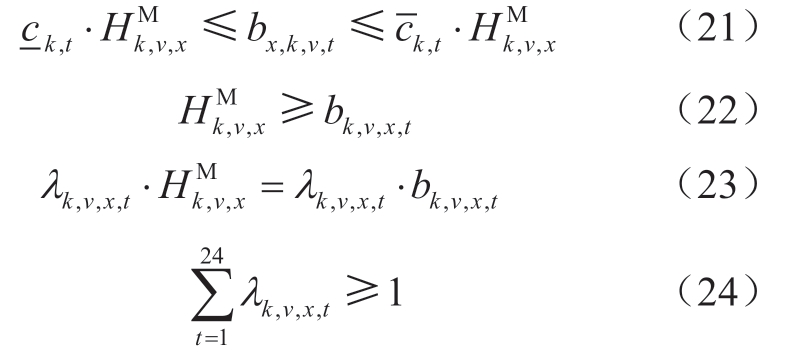
3）求解算法。

通过约束等效转换，可将模型转换为混合整数二次规划模型[29]，采用GUROBI商用求解器集成的分支定界法[30]进行模型求解。

2 实例分析

2.1 研究对象

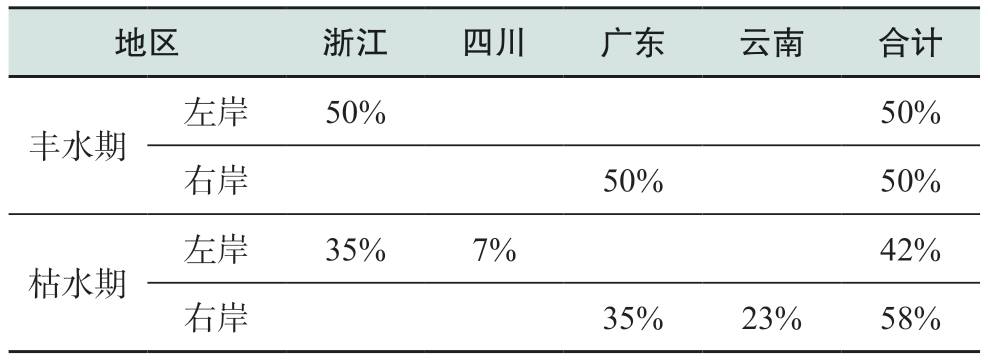
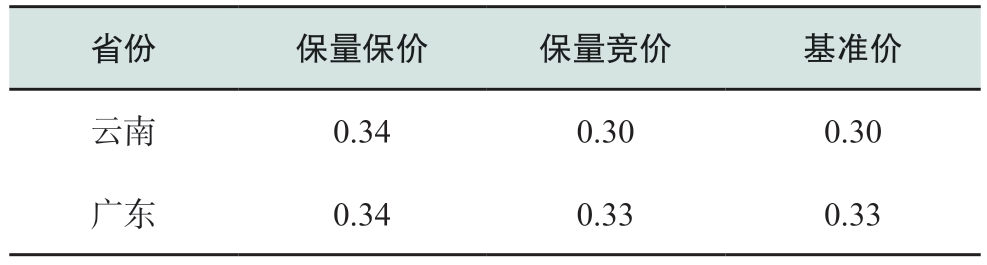
本文以金沙江下游溪洛渡右岸（简称溪右）水电站为研究对象。溪洛渡电站是金沙江干流“西电东送”重要骨干电源，位于四川和云南交界处，安装18台700 MW容量水电机组，左右岸各9台，总装机容量12 600 MW，丰水期（6月—10月）电力电量全部外送至广东和浙江，枯水期（11月—次年5月）满足云南、四川用电的情况下，剩余电量全部外送[15-16]。根据国家水电消纳安排，丰水期溪洛渡电站全部电量由浙江、广东按1∶1比例消纳；枯水期留存30%电量由云南、四川按1∶1比例消纳，其余电量由浙江、广东按1∶1比例消纳。考虑金沙江下游梯级水电站间的电量置换等原因，实际运行中，枯水期溪洛渡电站留存的30%电量按7∶23比例分别由四川、云南消纳，电量消纳方案详见表1。下文通过汛期、枯期2个不同实例进行验证分析。

表1 溪洛渡电站电量消纳方案
Table 1 Scheme for power consumption of Xiluodu Hydropower Plant

2.2 实例1：溪右电站枯期月度电量曲线分解

2.2.1 输入参数

溪洛渡右岸电站枯期实例中，模型的主要参数包括：广东、云南的电量比值R为1.5，计划总发电量Q为973.6 GWh，电站出力升降最小间隔时段数Δ为2，预测各旬最大出力Nxmax见表2，日分时申报单系数边界见表3、表4，各省、各品种的电价Pk,v见表5。

表2 溪洛渡右岸电站枯期各旬最大出力
Table 2 Maximum generation of right bank of Xiluodu Hydropower Plant in dry season MW

表3 溪洛渡右岸电站枯期分时系数下限
Table 3 Lower bound of hourly coefficients of right bank of Xiluodu Hydropower Plant in dry season

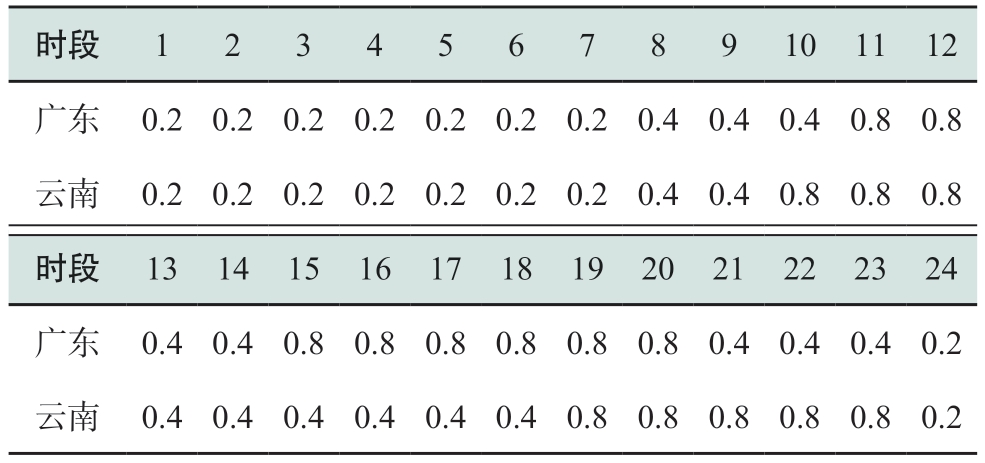
表4 溪洛渡右岸电站枯期分时系数上限
Table 4 Upper bound of hourly coefficients of right bank of Xiluodu Hydropower Plant in dry season

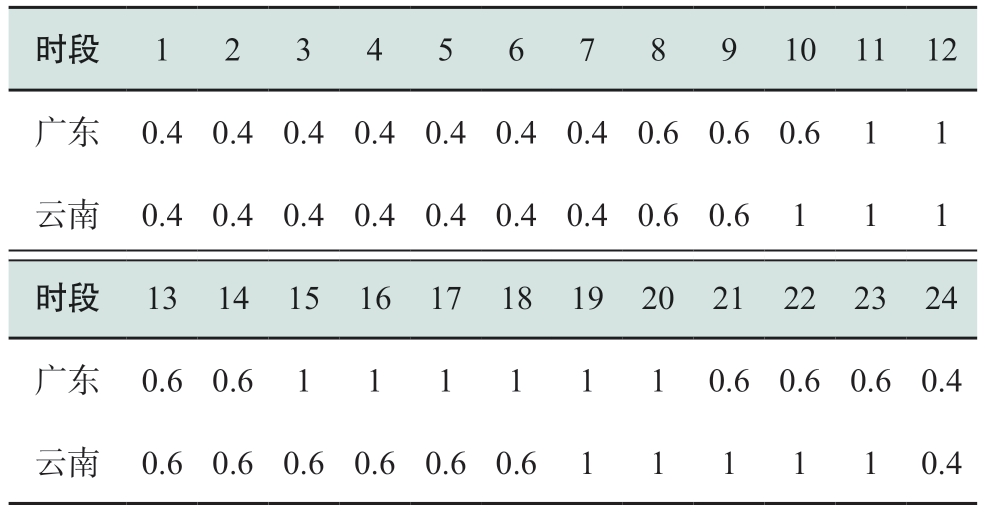
表5 枯期各省各品种电价
Table 5 Electricity price for each variety of two provinces in dry season元/kWh

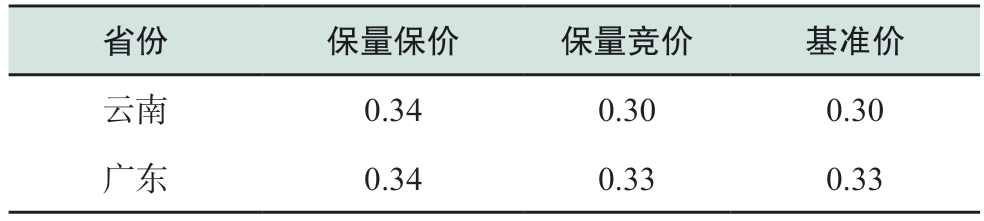
2.2.2 输出结果

按照第1章模型与方法可得到溪右电站送广东、云南两省，上、中、下旬逐日各品种的出力曲线，图1为溪右电站枯期上、中、下旬的出力过程图，图2、图3分别为枯期送广东、云南的各旬保量保价、保量竞价2种电量的分时系数，详细的曲线分解系数图见附录A，图4为溪右电站枯期各旬、各品种的出力分配过程。详细结果分析见2.4节。

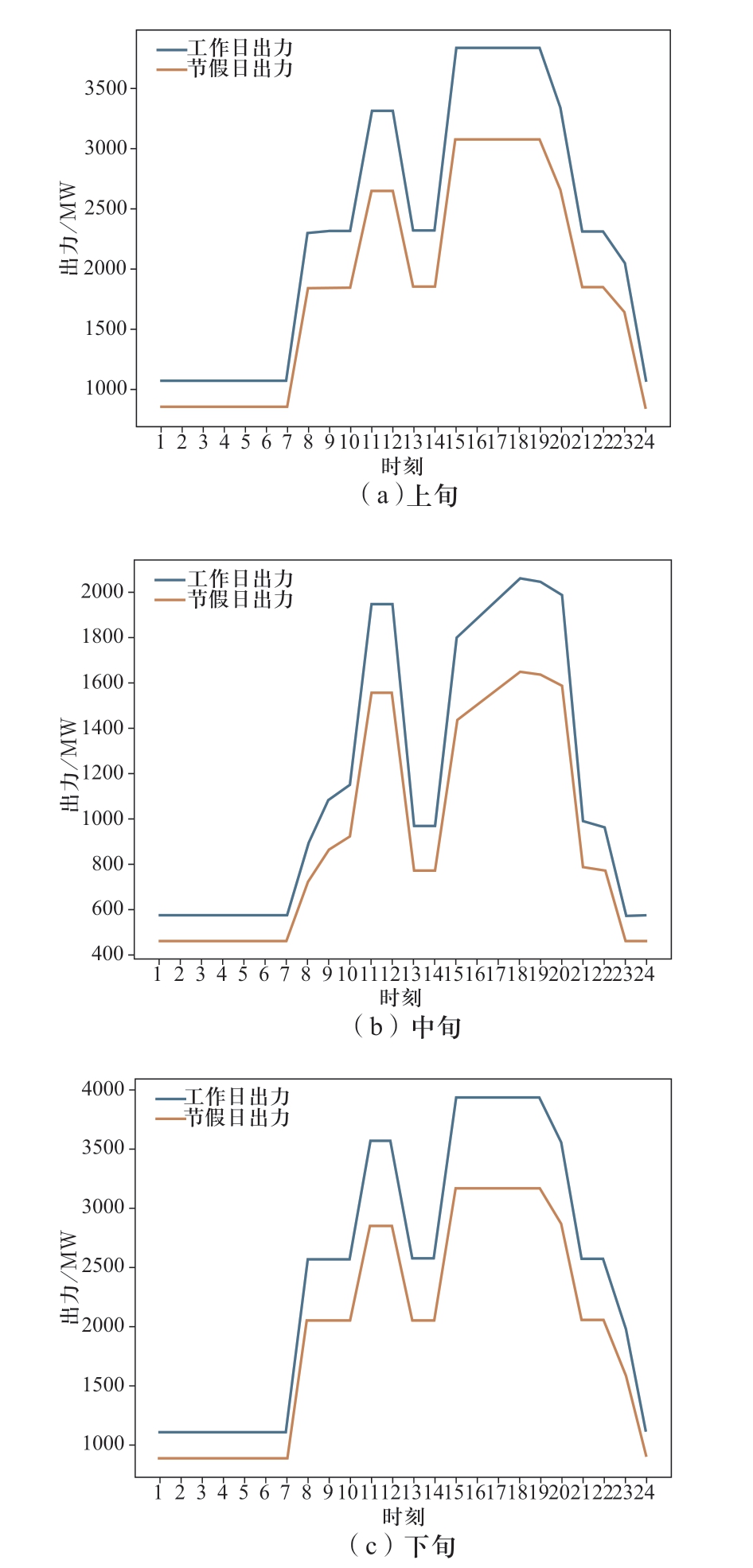
图1 溪洛渡右岸电站枯期上、中、下旬典型出力图
Fig.1 Typical outflow diagram of right bank of Xiluodu Hydropower Plant in the upper, middle, and late period in dry season

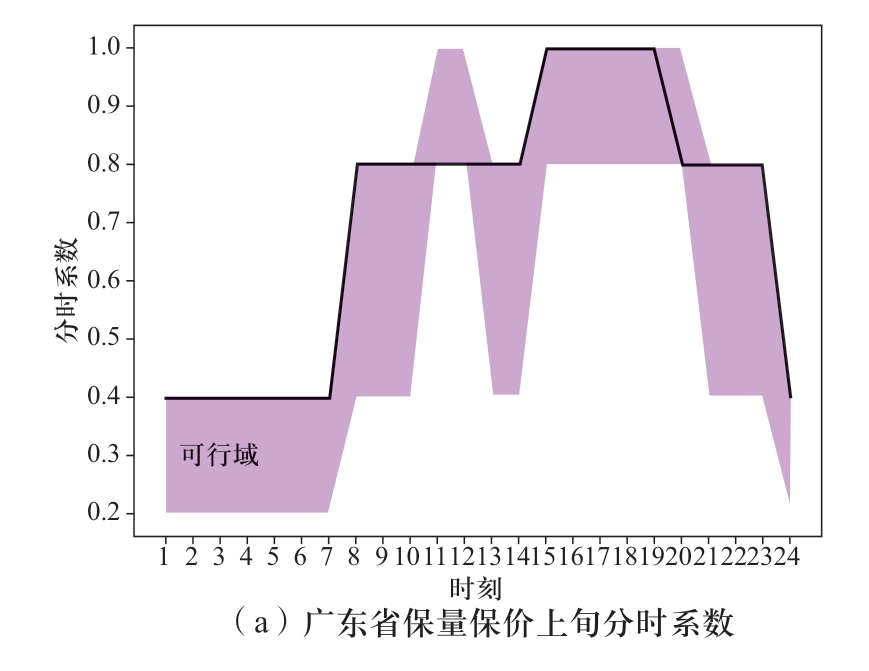
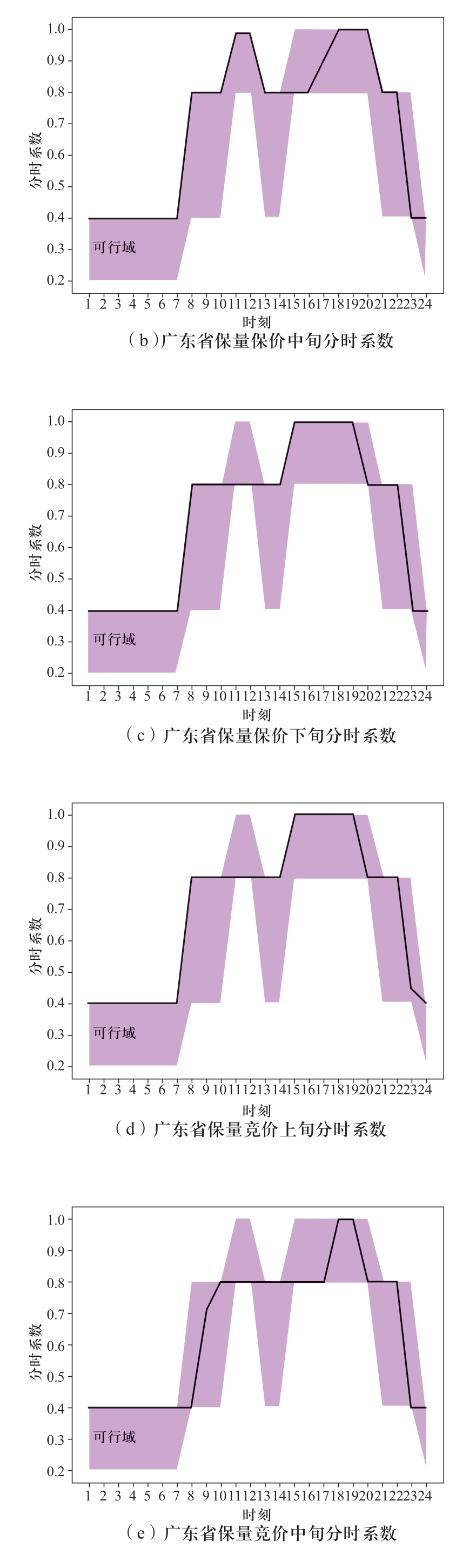
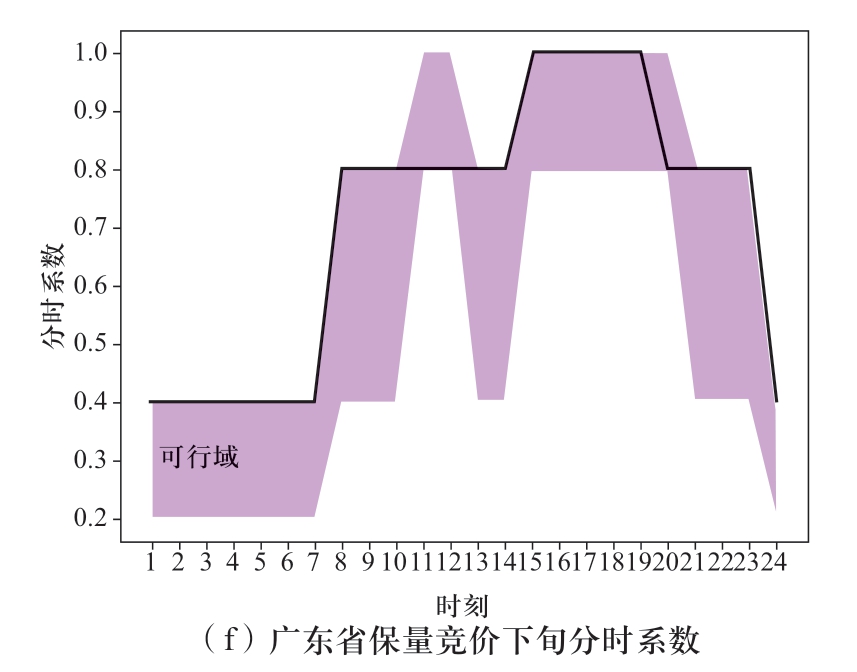
图2 枯期广东分时曲线
Fig.2 Time-sharing curve of Guangdong in dry season

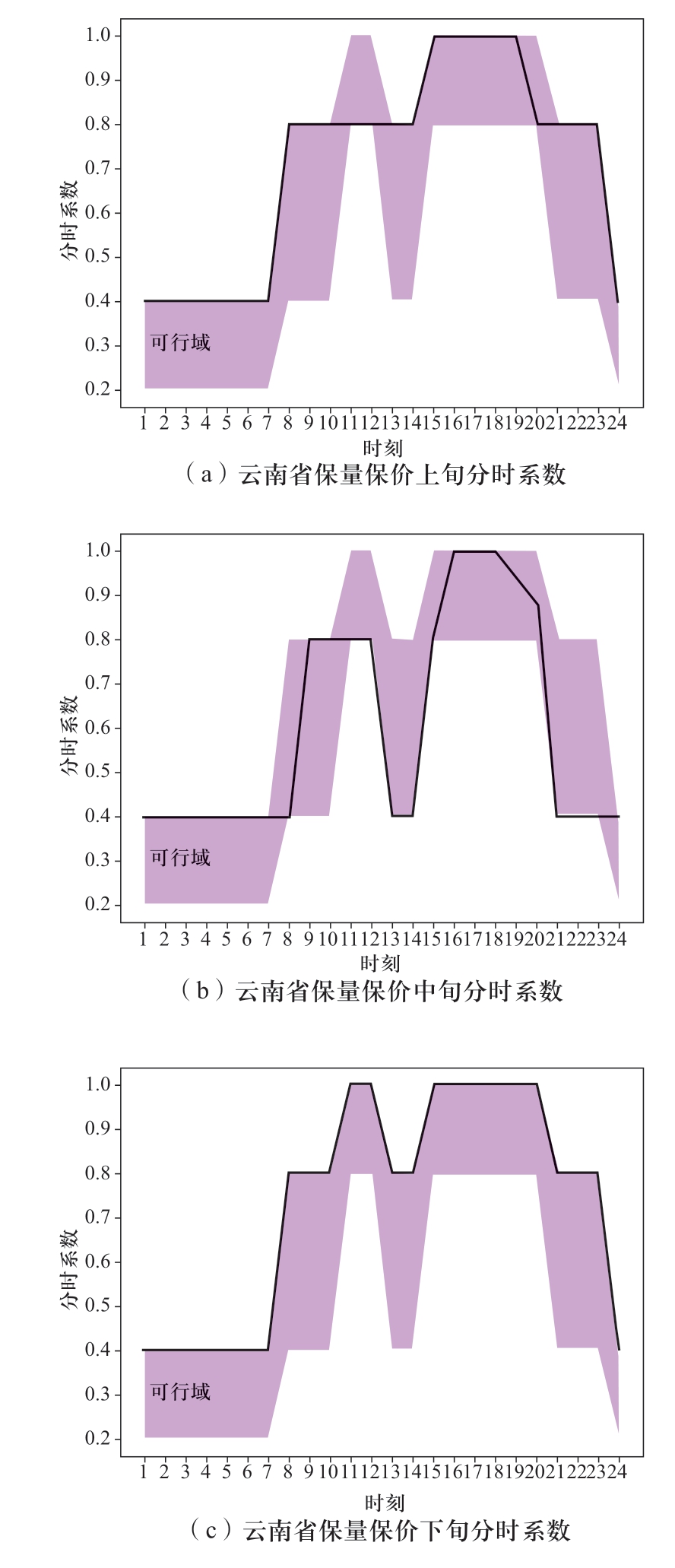
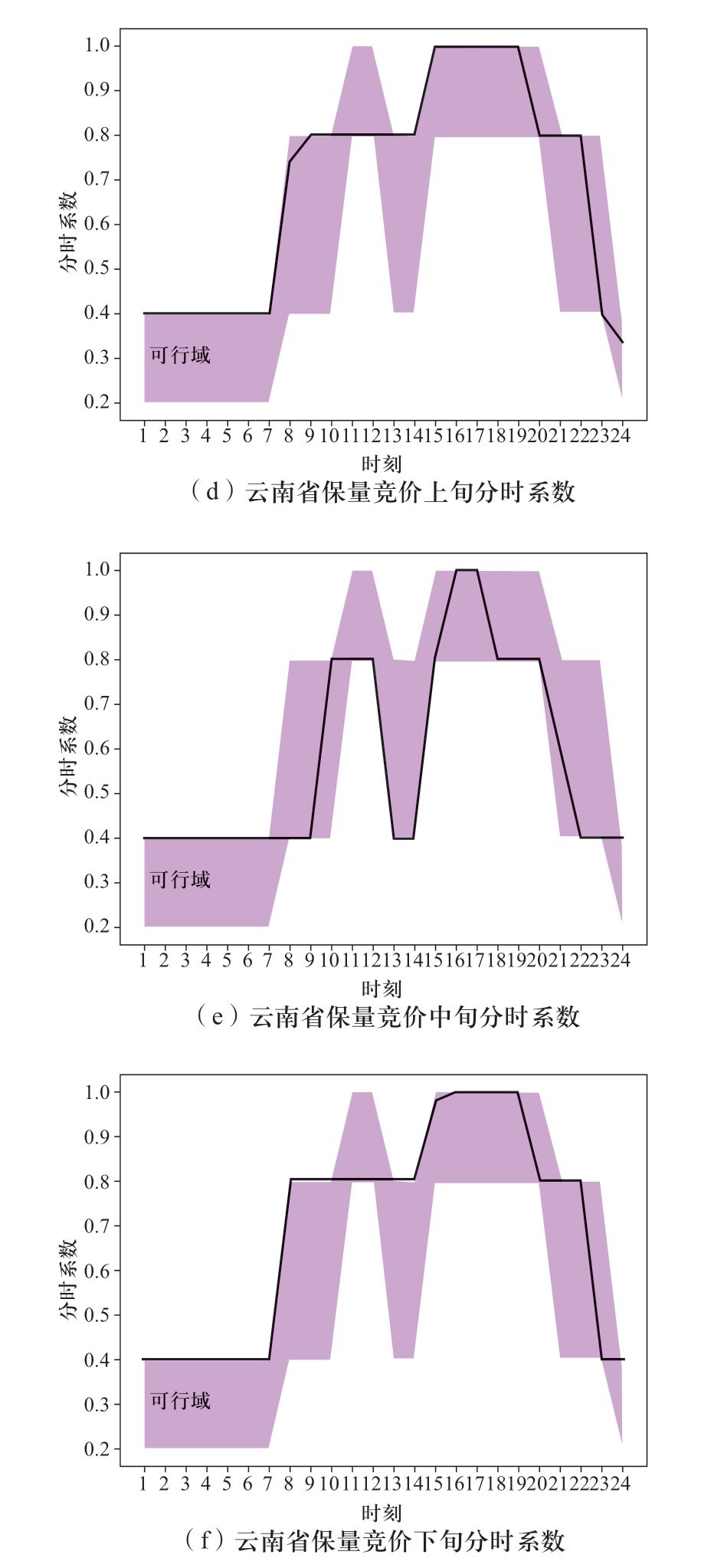
图3 枯期云南分时曲线
Fig.3 Time-sharing curve of Yunnan in dry season

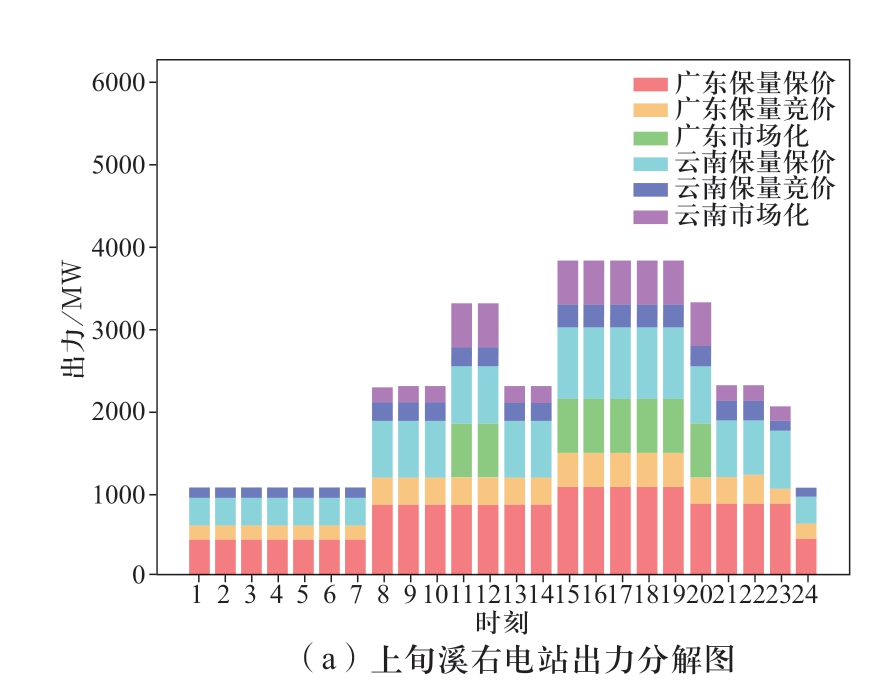
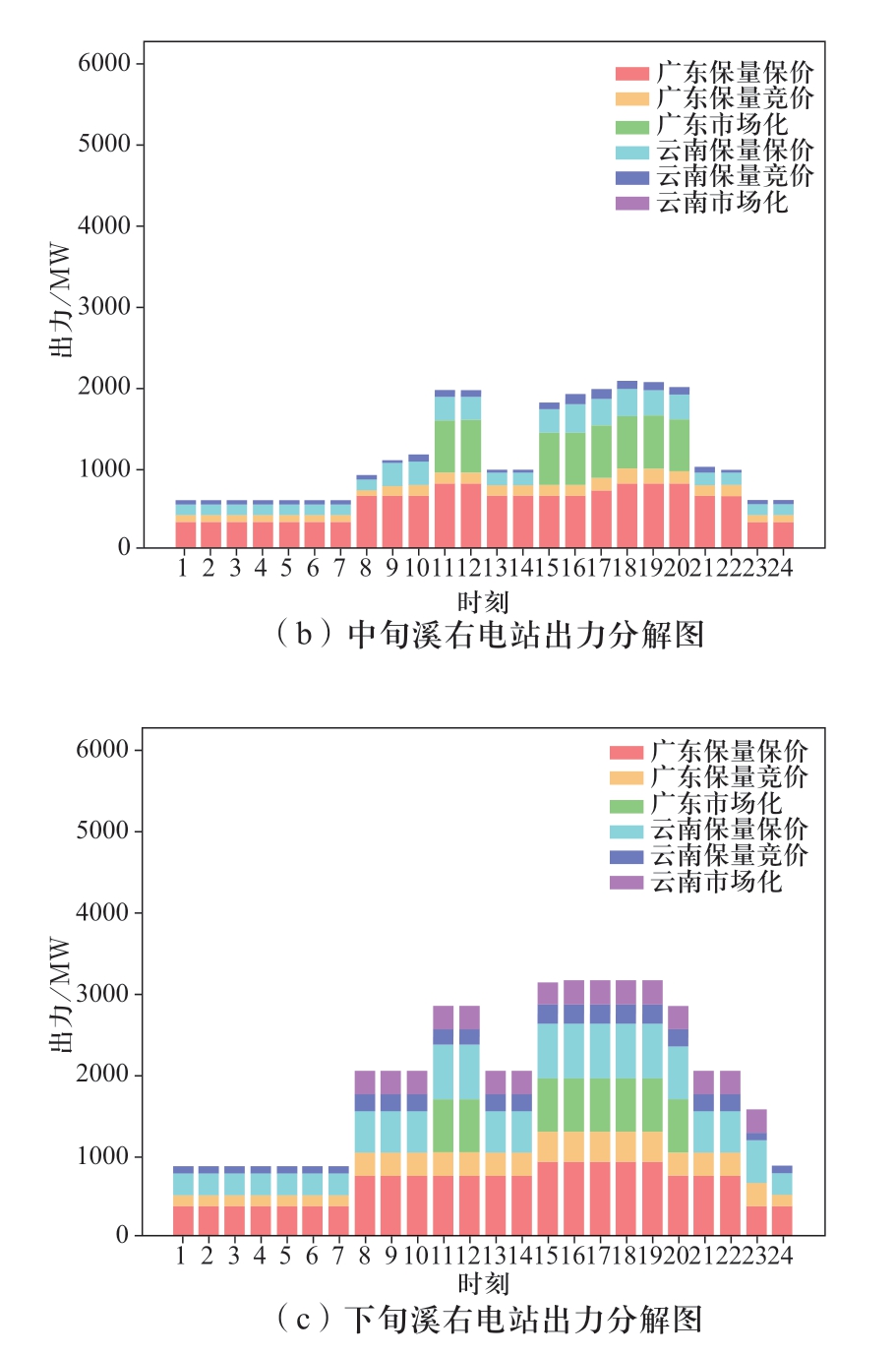
图4 溪洛渡右岸电站枯期出力曲线分解图
Fig.4 Output curve decomposition diagram of right bank of Xiluodu Hydropower Plant in dry season

2.3 实例2：溪右电站汛期月度电量曲线分解

2.3.1 输入参数

汛期实例中，模型的计划总发电量Q为1456.8 GWh，预测各旬最大出力Nxmax见表6，电站出力升降最小间隔时段数Δ为2，日分时申报单系数边界见表7、表8，各省、各品种的电价Pk,v见表9。

表6 溪洛渡右岸电站汛期各旬最大出力
Table 6 Maximum generation of right bank of Xiluodu Hydropower Plant in flood season MW

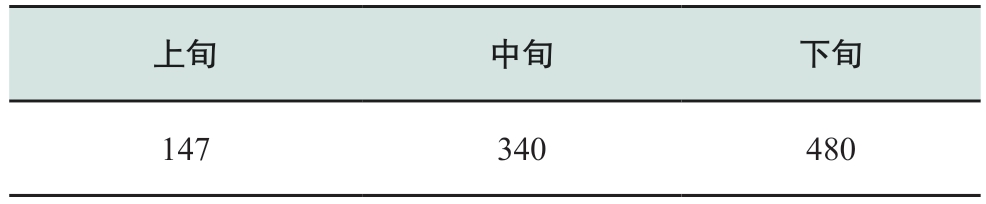
表7 溪洛渡右岸电站汛期分时系数下限
Table 7 Lower bound of hourly coefficients of right bank of Xiluodu Hydropower Plant in flood season

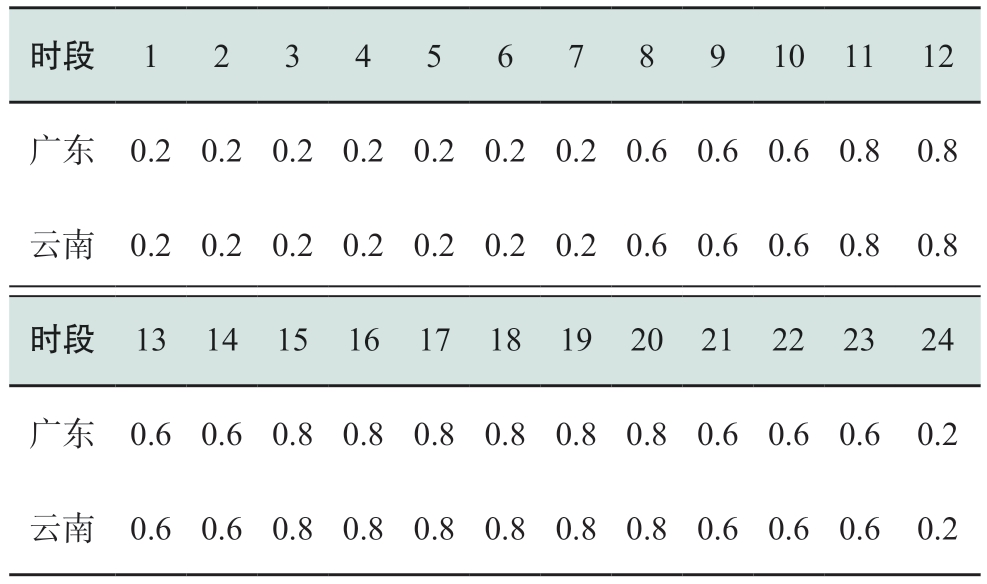
表8 溪洛渡右岸电站汛期分时系数上限
Table 8 Upper bound of hourly coefficients of right bank of Xiluodu Hydropower Plant in flood season

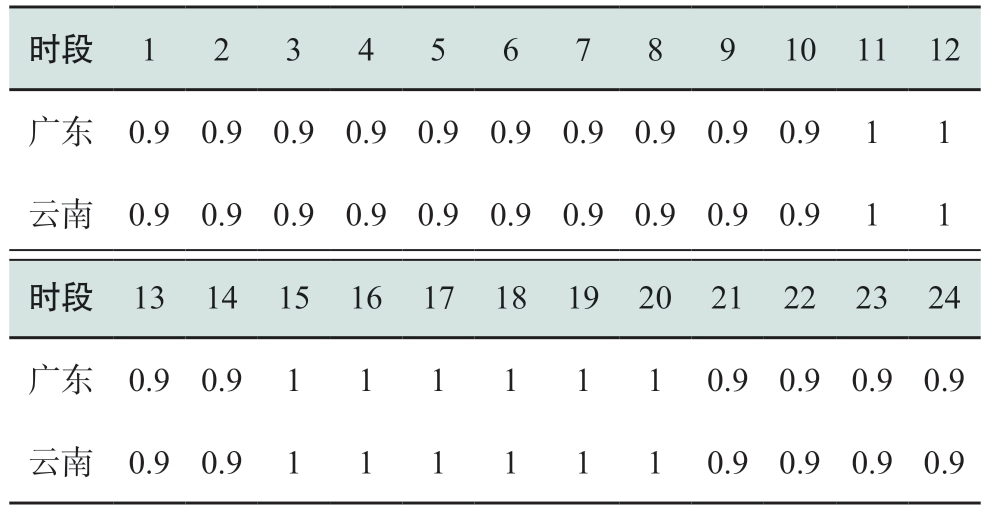
表9 汛期各省各品种电价
Table 9 Electricity price for each variety of two provinces in flood season元/kWh

2.3.2 输出结果

图5为溪右电站汛期上、中、下旬的出力过程图，图6为汛期送广东上、中、下旬的保量保价、保量竞价2种电量的分时系数，详细的曲线分解系数图见附录A，图7为溪右电站汛期上、中、下旬各品种的出力分配过程。详细结果分析见2.4节。

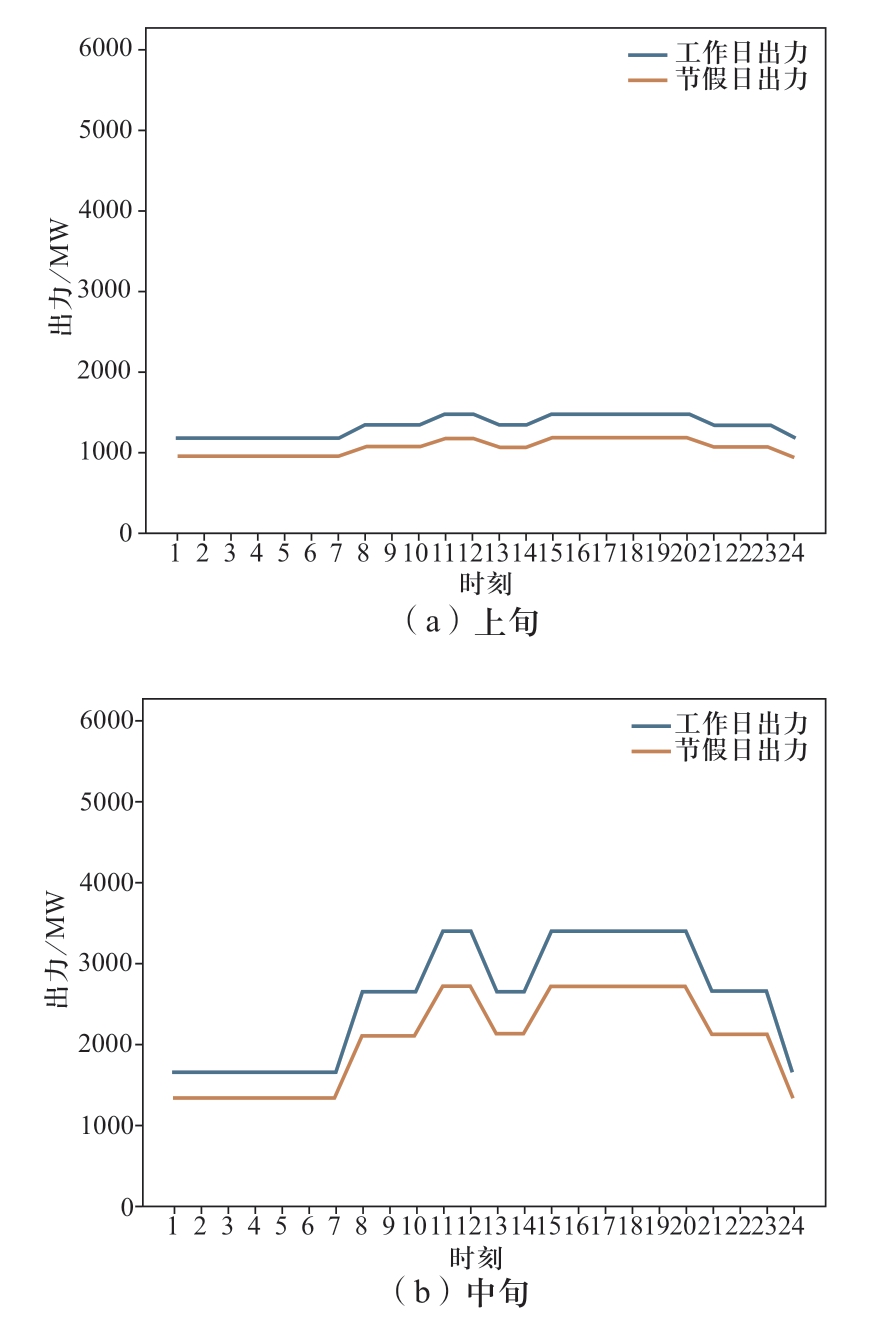
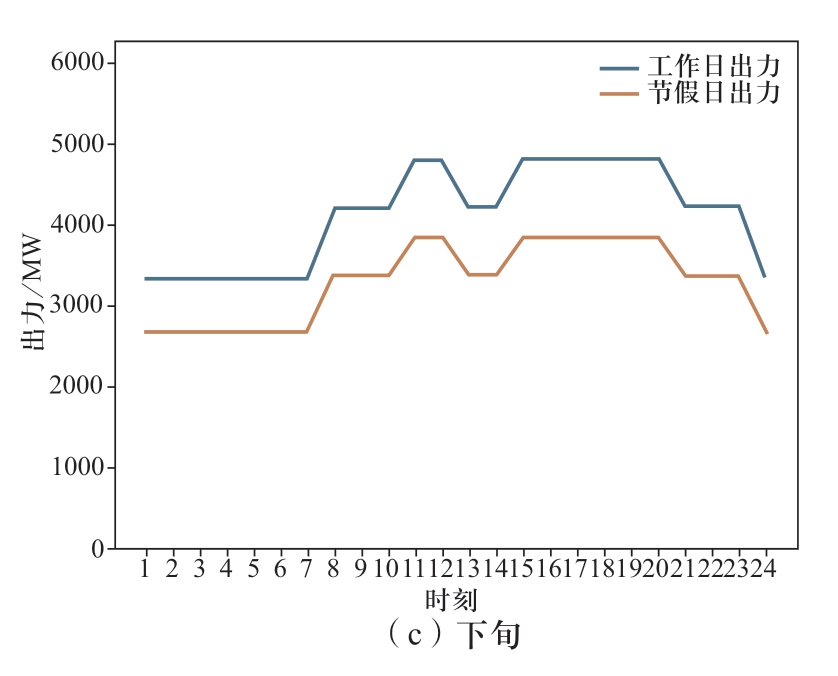
图5 溪洛渡右岸电站汛期上、中、下旬典型出力图
Fig.5 Typical outflow diagram of right bank of Xiluodu Hydropower Plant in the upper, middle, and late period in flood season

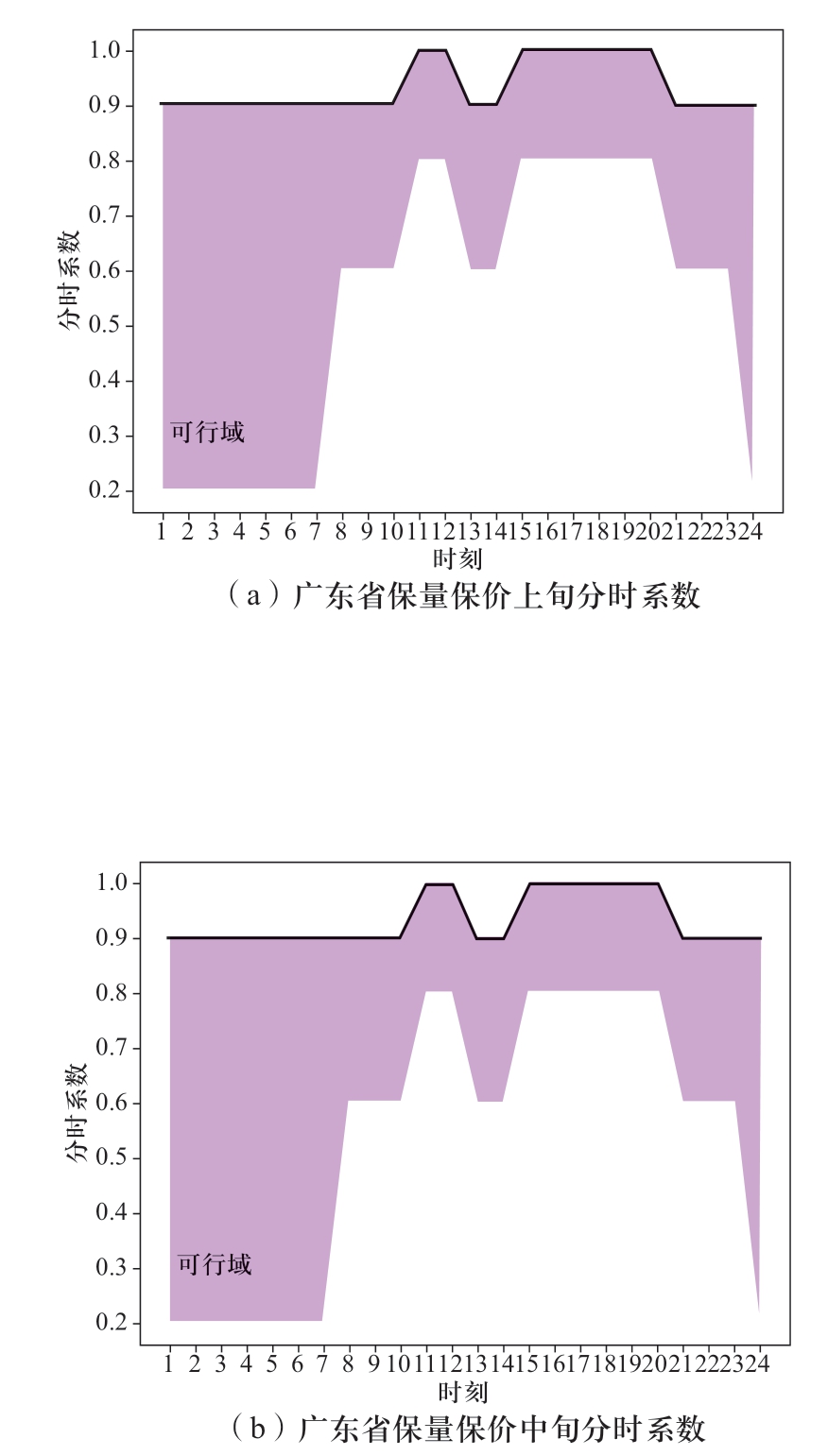
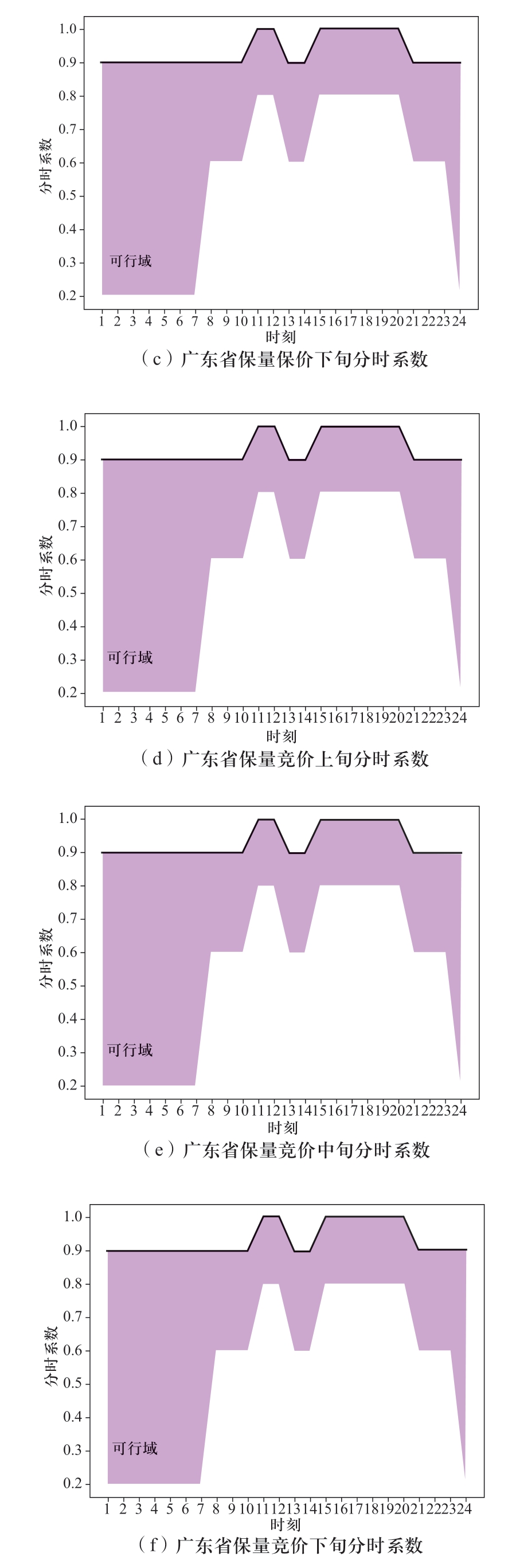
图6 汛期广东分时曲线
Fig.6 Time-sharing curve of Guangdong in flood season

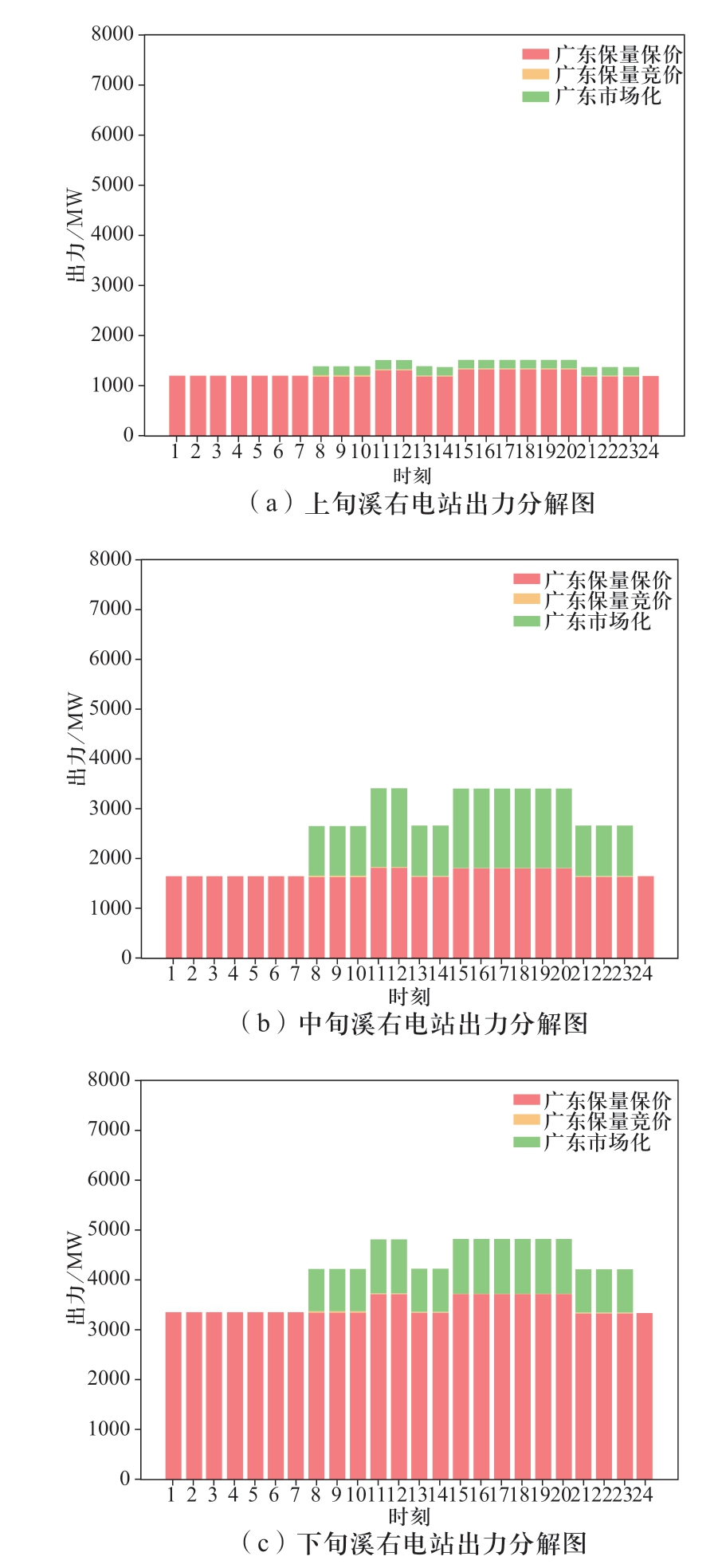
图7 溪洛渡右岸电站汛期出力曲线分解图
Fig.7 Output curve decomposition diagram of right bank of Xiluodu Hydropower Plant in flood season

2.4 结果分析

结合枯期、汛期两个不同边界条件的计算结果，分析溪右电站月度电量曲线分解的合理性与高效性。

在合理性方面，枯期实例中溪右电站月度总电量为973.6 GWh，送广东与云南电量分别为584 GWh、389.6 GWh，计算结果完全满足给定的跨省送电比例要求；保量保价与保量竞价2个优先电量品种分别为725.6 GWh、248 GWh，得到的结果与给定的参数一致，同时按照两省的分配比例要求，各品种电量分配结果也与规定的送电比例一致。

如图4枯期出力分解结果所示，上、中、下旬最大出力均满足表2中设置的枯期各旬最大出力。经计算，各省、各旬内保量保价与保量竞价电量比值均在月度保量保价总量与保量竞价总量比值的±20%允许波动范围内，满足给定的边界要求；图2、图3是模型得到的分旬、分时系数，均在给定的取值范围内，具体的取值边界见表3、表4，说明模型得到的曲线分解结果充分满足了电网对溪右电站提出的调峰要求。同理，进一步分析汛期的计算结果，汛期溪右电站仅送广东，所以广东受电量即为溪右电站的月度发电量，保量保价的电量为1456.8 GWh，与给定的参数一致。图6是模型得到的广东分旬、分时系数取值，均在给定的上下限内，满足模型设置的分时系数边界（见表7、表8）。从2个实例中电站的分时出力曲线来看，上、中、下旬各品种、各时段的出力之和均与溪右电站的总出力相等，满足逐时段的电力平衡约束。综合可见，模型得到的曲线分解结果满足给定的各项约束边界要求。

进一步分析模型优化结果的高效性。从枯期月份的电量分解结果来看，在满足电网调峰要求的前提下，溪右电站在上、中、下旬的市场化电量基本都分配在电价相对较高的负荷高峰与平段（见图4），其中广东全部市场化电量都分配在高峰时段，原因是其市场化电量在高峰时段的电价最高，即基准价的1.1倍，为最大化水电站的发电收益，这种分配方式是合理的。云南63%市场化电量安排在负荷高峰时段、37%安排在负荷平段，主要是云南的市场化电价低于广东，通过跨省多品种协调优化配置，优先将市场化电量安排在所有市场中电价最高的广东高峰时段，为满足云南保量保价、保量竞价2个品种的跨省电量比例要求，云南高峰时段需要安排较大比例的优先电量，所以有一部分市场化电量被分配在负荷平段。同理，结合汛期月份的电量分解结果，由于溪右电站仅送电广东，在上、中、下旬保量保价和保量竞价优先电量品种的分时系数均是按照规定的谷峰比，以响应电网调峰要求，同时最大程度地为市场化电量安排腾出了高峰和平段的负荷空间，这一点通过图6和图7可以直观看出。综上所述，溪右电站电量的曲线分解结果是可行且高效的。

3 结论 

中国西南地区很多干流巨型水电站承担跨省、跨区复杂送电任务，面临的发电调度、市场化运行需求与约束条件具有很强的时空耦合性，给电站的电量与电力分配带来很大困难，已成为水电企业实际生产面临的重要难题。本文依托溪洛渡水电站实际工程，提出了溪右电站月度合同电量曲线分解模型，通过月度实际数据验证分析，得到如下结论。

1）构建的月度电量曲线分解模型能够适应枯期、汛期不同电量规模下多省、多市场品种、多个尺度下的电量分解要求，得到的调度方案符合实际生产习惯，体现了较好的适应性和实用性。

2）在考虑多个电网差异化调峰要求的同时，以溪右电站月度电量收益最大为目标，能够有效兼顾电网和水电企业多方利益，得到的月度电量申报单上、中、下旬的分时系数过程与峰平谷趋势契合，在调峰边界条件内市场化电量尽可能安排在电价较高的负荷峰段和平段，较为合理。

3）该模型主要面向西南巨型水电站跨省跨市场多维电量曲线分解任务，这类任务是金沙江、澜沧江、雅砻江等流域干流主要水电站面临的共性需求，可以为水电企业编制月度、年度等交易申报单提供理论支持。

附录A 溪洛渡右岸电站电量曲线分解图

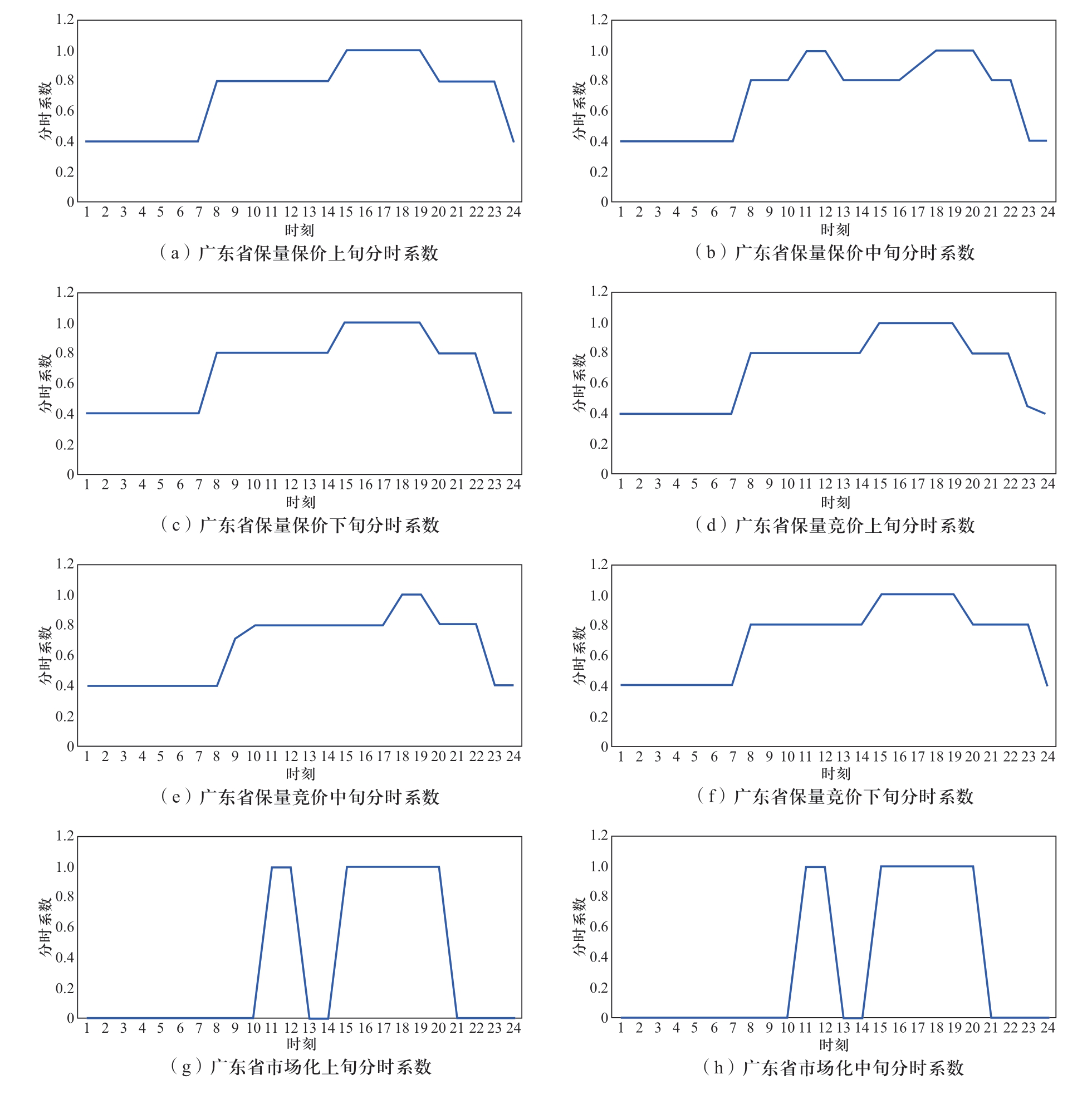
图A1 溪洛渡右岸电站枯期合同电量曲线分解图
Fig.A1 Decomposition diagram of contract electricity curve of right bank of Xiluodu Hydropower Plant during dry period

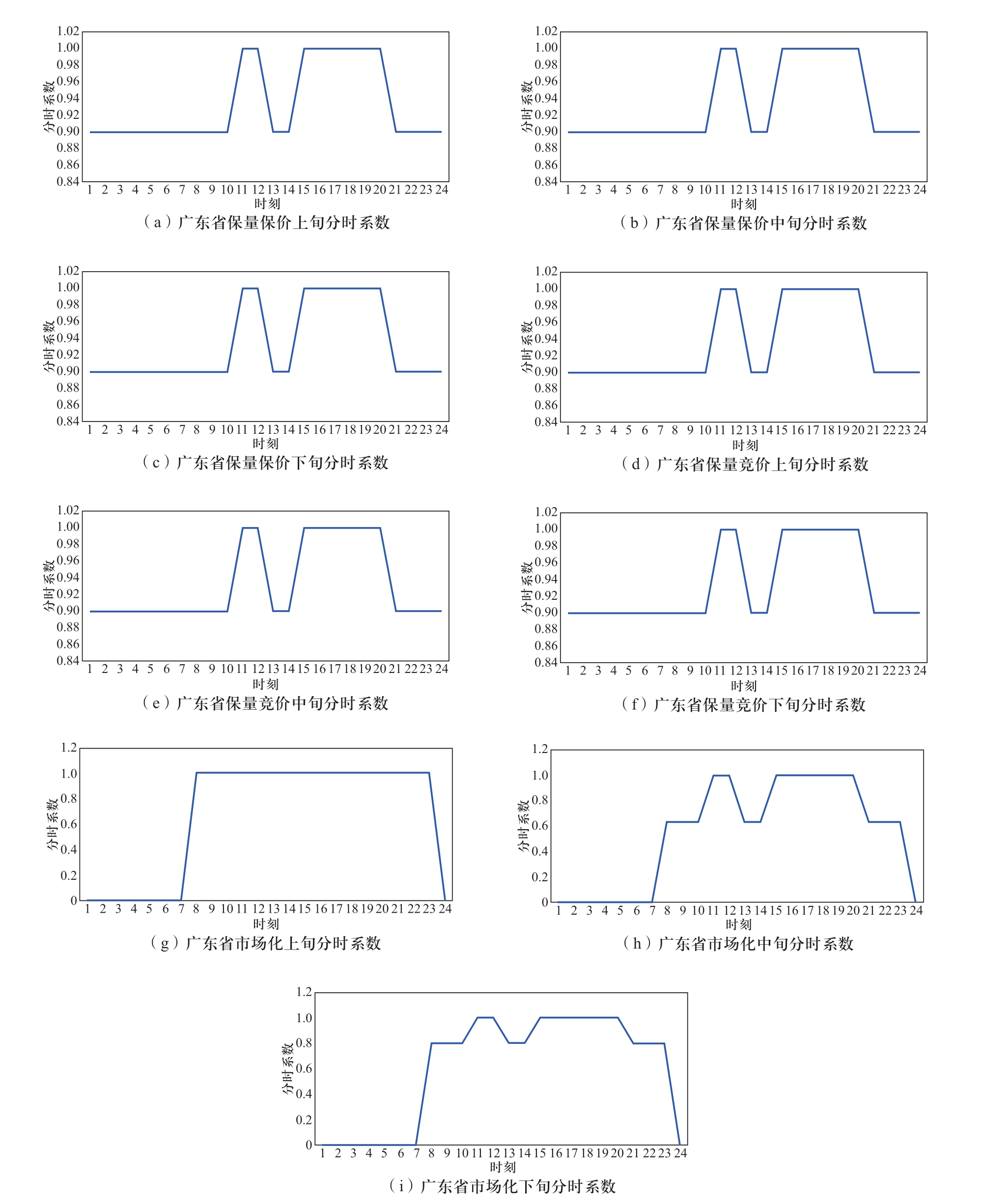
图A2 溪洛渡右岸电站汛期合同电量曲线分解图
Fig.A2 Decomposition diagram of contract electricity curve of right bank of Xiluodu Hydropower Plant during flood period

参考文献

[1] FANG B, QIU W, WANG M, et al.Evaluation index system of shared energy storage market towards renewable energy accommodation scenario: a China’s Qinghai Province context[J].Global Energy Interconnection, 2022, 5(1): 77-95.

[2] 黄际元，杨俊，黄治国，等.基于扩展短期预测和动态优化的储能调峰策略[J].太阳能学报，2021，42(9)：470-476.HUANG Jiyuan, YANG Jun, HUANG Zhiguo, et al.Control strategy of energy storage power station participating in power grid peak shaving based on extended short-term load forecasting and dynamic optimization[J].Acta Energiae Solaris Sinica, 2021, 42(9): 470-476 (in Chinese).

[3] GUO Y J, TIAN X Q, XU T, et al.Economic analysis of deep peak-shaving reform of 600 MW thermal power unit in Beijing-Tianjin-Tangshan power grid[J].IOP Conference Series: Earth and Environmental Science, 2021, 661(1): 012018.

[4] YANG J, LIU C, MI Y, et al.Optimization operation model of electricity market considering renewable energy accommodation and flexibility requirement[J].Global Energy Interconnection, 2021, 4(3): 227-238.

[5] 史普鑫，史沛然，王佩雯，等.华北区域电力调峰辅助服务市场分析与运行评估[J].电力系统自动化，2021，45(20)：175-184.SHI Puxin, SHI Peiran, WANG Peiwen, et al.Analysis and operation evaluation of power peak-shaving ancillary service market in North China[J].Automation of Electric Power Systems, 2021, 45(20): 175-184 (in Chinese).

[6] 臧海祥，马铭欣，周亦洲，等.电力市场环境下风电-光热-生物质混合电站鲁棒优化调度模型[J].电力系统保护与控制，2022，50(5)：1-11.ZANG Haixiang, MA Mingxin, ZHOU Yizhou, et al.Robust optimal scheduling model for a ‘wind power-concentrating solar power-biomass’ hybrid power plant in the electricity market[J].Power System Protection and Control, 2022, 50(5):1-11 (in Chinese).

[7] 国雪健，李思远，朱秋萍，等.基于均衡模型的寡头电力市场容量机制研究[J].电力系统保护与控制，2021，49(24)：121-131.GUO Xuejian, LI Siyuan, ZHU Qiuping, et al.Capacity mechanisms of the oligopoly electricity market based on an equilibrium model[J].Power System Protection and Control,2021, 49(24): 121-131 (in Chinese).

[8] 李东东，段维伊，周波，等.基于主成分分析的电力市场供应侧主体竞争潜力指数研究[J].电力系统保护与控制，2020，48(19)：1-8.LI Dongdong, DUAN Weiyi, ZHOU Bo, et al.Competitive potential index of the supply side of the market entity based on principal component analysis[J].Power System Protection and Control, 2020, 48(19): 1-8 (in Chinese).

[9] 韩小齐，刘文颖，庞清仑，等.考虑日前现货市场风险的电力负荷参与系统调峰控制模型[J].电力系统保护与控制，2022，50(17)：55-67.HAN Xiaoqi, LIU Wenying, PANG Qinglun, et al.Peak shaving control model of power load participation system considering day-ahead spot market risk[J].Power System Protection and Control, 2022, 50(17): 55-67(in Chinese).

[10] 杨苹，曾凯林，余雁琳，等.电能量市场下负荷聚合商参与负荷削减投标策略[J].电力工程技术，2022，41(1)：2-10.YANG Ping, ZENG Kailin, YU Yanlin, et al.Strategy of load aggregator participating in load curtailment bidding under power market[J].Electric Power Engineering Technology,2022, 41(1): 2-10 (in Chinese).

[11] SHEN J J, ZHANG X F, WANG J, et al.Optimal operation of interprovincial hydropower system including Xiluodu and local plants in multiple recipient regions[J].Energies, 2019, 12(1):144.

[12] 何绍坤，郭生练，刘攀，等.金沙江梯级与三峡水库群联合蓄水优化调度[J].水力发电学报，2019，38(8)：27-36.HE Shaokun, GUO Shenglian, LIU Pan, et al.Joint and optimal impoundment oepration of Jinsha River’s cascade reservoirs and Three Gorges Reservoir[J].Journal of Hydroelectric Engineering, 2019, 38(8): 27-36 (in Chinese).

[13] 丁斌，邢志坤，王帆，等.考虑多元负荷需求响应的综合智慧能源系统协同优化调度[J].全球能源互联网，2022,5(6)：583-592.DING Bin, XING Zhikun, WANG Fan, et al.Collaborative optimal scheduling of integrated smart energy system considering multi-load demand response[J].Journal of Global Energy Interconnection, 2022, 5(6): 583-592 (in Chinese).

[14] 王漪，于继来，柳焯.基于月度竞价空间滚动均衡化的年中标电量分解[J].电力系统自动化，2006，30(17)：24-27.WANG Yi, YU Jilai, LIU Zhuo.Decomposition of yearly bided volume based on roll-uniformization of monthly competitive bidding spaces[J].Automation of Electric Power Systems, 2006, 30(17): 24-27 (in Chinese).

[15] 程雄，唐应玲，申建建，等.电力市场环境下大规模水电站群月度交易电量分解与校核方法[J].中国电机工程学报，2020，40(8)：2514-2525.CHENG Xiong, TANG Yingling, SHEN Jianjian, et al.Decomposition and checking method for large-scale hydropower plants monthly trading energy in electricity market[J].Proceedings of the CSEE, 2020, 40(8): 2514-2525(in Chinese).

[16] 谢蒙飞，贾泽斌，张帆，等.计及电量分解的高比例水电电网短期调度方法[J].水力发电学报，2021，40(1)：54-64.XIE Mengfei, JIA Zebin, ZHANG Fan, et al.Method of short-term scheduling for high-proportion hydropower grid considering energy decomposition[J].Journal of Hydroelectric Engineering, 2021, 40(1): 54-64 (in Chinese).

[17] 许传龙，张粒子，陈大宇，等.基于预招标的月度偏差电量平衡机制及其多周期发电调度优化模型[J].中国电机工程学报，2019，39(17)：5085-5094.XU Chuanlong, ZHANG Lizi, CHEN Dayu, et al.A monthly balancing mechanism based on pre-bidding and its multiperiod generation schedule optimization model[J].Proceedings of the CSEE, 2019, 39(17): 5085-5094 (in Chinese).

[18] 于旭光，李刚，李亚鹏，等.耦合日合同分解及日前市场竞价的梯级水电站短期鲁棒优化调度[J].电网技术，2021，45(10)：4016-4025.YU Xuguang, LI Gang, LI Yapeng, et al.Short-term robust optimization scheduling of cascade hydropower stations coupled with daily contract decomposition and day-ahead market bidding[J].Power System Technology, 2021, 45(10):4016-4025 (in Chinese).

[19] 于旭光，李亚鹏，贾泽斌，等.考虑现货市场竞价空间的梯级水电站中长期合同电量分解模型[J].电力系统自动化，2021，45(6)：62-71.YU Xuguang, LI Yapeng, JIA Zebin, et al.Medium-and long-term contract energy decomposition model for cascade hydropower station considering spot market bidding space[J].Automation of Electric Power Systems, 2021, 45(6): 62-71 (in Chinese).

[20] 苗树敏，罗彬，申建建，等.考虑市场过渡和中长期合约电量分解的水火电短期多目标发电调度[J].电网技术，2018，42(7)：2221-2231.MIAO Shumin, LUO Bin, SHEN Jianjian, et al.Short-term multi-objective hydro-thermal generation dispatch considering electricity market transition and mid- and long-term contract decomposition[J].Power System Technology, 2018, 42(7):2221-2231 (in Chinese).

[21] 张少华，刘帅，王晛，等.基于分布鲁棒优化的发电商中长期合同电量分解模型[J].电力系统保护与控制，2023，51(1)：71-80.ZHANG Shaohua, LIU Shuai, WANG Xian, et al.A distributionally robust optimization model for power generators’ medium and long-term contracted energy decomposition[J].Power System Protection and Control, 2023,51(1): 71-80 (in Chinese).

[22] 邹屹东，钱晶，张文英，等.基于CPSOGSA算法的风-光-小水电微电网负荷频率最优H2/H∞鲁棒控制[J].电力系统保护与控制，2022，50(11)：42-51.ZOU Yidong, QIAN Jing, ZHANG Wenying, et al.Optimal H2/H∞ robust control for the load frequency of a microgrid including wind power-photovoltaic-small hydropower based on CPSOGSA[J].Power System Protection and Control, 2022,50(11): 42-51 (in Chinese).

[23] 李飞，李咸善，李振兴，等.基于梯级水电调节的多能联合发电系统短期优化调度[J].电力系统保护与控制，2022，50(15)：11-20.LI Fei, LI Xianshan, LI Zhenxing, et al.Short-term optimal scheduling of multi-energy combined generation systems based on the regulation of cascade hydropower stations[J].Power System Protection and Control, 2022, 50(15): 11-20 (in Chinese).

[24] MU C F, XING Y H, ZHANG F, et al.The coordination mechanism of forward market and spot market under the costbased electricity market model for Yunnan[C]//2021 6th Asia Conference on Power and Electrical Engineering (ACPEE).April 8-11, 2021.Chongqing, China.IEEE, 2021.

[25] YIN S, WANG S Q, YANG Q C, et al.Research on the development of domestic and foreign electricity sales markets serving the construction of electricity retail markets[J].IOP Conference Series: Earth and Environmental Science, 2021,651(2): 022021.

[26] BOJNEC Š, KRIŽAJ A.Electricity markets during the liberalization: the case of a European Union country[J].Energies, 2021, 14(14): 4317.

[27] LIU X R, ZHOU N, WU D N.Information disclosure mechanism and practice under electricity market regulation[C]//2022 China International Conference on Electricity Distribution (CICED).September 7-8, 2022.Changsha, China.IEEE, 2022.

[28] STEEGER G, BARROSO L A, REBENNACK S.Optimal bidding strategies for hydro-electric producers: a literature survey[J].IEEE Transactions on Power Systems, 2014, 29(4):1758-1766.

[29] 曾雪婷，刘天琪，李茜，等.高水电比重系统电力电量平衡混合整数二次规划模型及算法研究[J].中国电机工程学报，2017，37(4)：1114-1125.ZENG Xueting, LIU Tianqi, LI Qian, et al.An mixed integer quadratic programming model and algorithm study for power balance problem of high hydropower proportion’s system[J].Proceedings of the CSEE, 2017, 37(4): 1114-1125 (in Chinese).

[30] GAU C Y, SCHRAGE L E.Implementation and testing of a branch-and-bound based method for deterministic global optimization: operations research applications[M]//Nonconvex Optimization and Its Applications.Boston, MA: Springer US,2004: 145-164.

Model for Curve Decomposition of Monthly Contract Electricity of Hydropower Plant

HU Xiaoyong1, HAN Xu2, CHEN Yuchen1, FAN Chenkai1, XU Tianyao1, SHEN Jianjian2*, CHENG Chuntian2
(1.China Three Gorges Corporation Electricity Market Research Center, Haidian District, Beijing 100086, China;2.Dalian University of Technology, Dalian 116023, Liaoning Province, China)

Abstract: The trans-provincial and trans-regional power transmission of large hydropower plant involves the decomposition of power curve among multiple provinces,multiple varieties and multiple time scales, and needs to consider the needs of complex peak shaving in power grids.This is an important problem to be solved in the monthly power generation and operation of the power plant.Based on the production demand of real engineering, this paper constructs a monthly contract power curve decomposition model, which is suitable for trans-provincial and trans-regional power transmission of giant hydropower plants.Considering the differences of electricity prices of three types of hydropower plants, including guaranteed quantity and guaranteed price, guaranteed quantity bidding and marketization, as well as the complex constraints of power grid peak shaving, market and power station operation, this paper puts forward the secondary planning goal of maximizing the total revenue of multi-provincial and multi-variety power generation.The mixed integer linear programming method is used to solve the model efficiently.The model is verified by two different application scenarios of right bank of Xiluodu Hydropower Plant in dry season and flood season.The results show that under the boundary conditions of peak shaving meeting the requirements of power grid, by optimizing the multi-scale and multi-variety power and output distribution of the two provinces, the market-oriented power is preferentially distributed to the peak and flat sections of load, the power generation income of right bank of Xiluodu Hydropower Plant can be effectively improved.

Keywords: electricity market; contract electricity; generation curve; peak-shaving

作者简介：

胡晓勇

胡晓勇（1974），男，硕士研究生，研究方向为电力市场营销、水库调度，E-mail：chhchxy@126.com。

申建建（1984），男，教授，博士生导师，主要从事水电调度、水风光多能互补、电力市场等研究。通信作者，E-mail：shenjj@dlut.edu.cn。

（责任编辑 李锡）