0 引言

电压源换流器高压直流（voltage sourced converter high voltage direct current，VSC-HVDC）输电系统作为新一代直流输电技术，具有向无源电网（孤岛）供电、快速独立控制有功与无功、潮流反转快、运行方式灵活等优点[1-4]，国际上已成功应用于风电并网、电网互联、孤岛和弱电网供电、城市供电等领域[5-8]。国内将其统称为柔性直流输电系统（以下简称“柔性直流”）。

目前电网规划的方式计算中是以三相短路电流计算结果作为开关遮断电流是否超标的判断依据，常用的短路电流计算程序均为机电暂态仿真软件。由于早期柔性直流容量较小，国际上普遍使用的IEC 60909和ANSI短路电流计算标准以及短路电流计算国家标准中均忽略了交流系统发生短路故障时直流系统对短路电流的贡献[9-10]，其短路电流忽略不计。但随着柔性直流容量的增加，其在故障期间提供的短路电流已不可忽视，特别是厦门工程、张北工程和白鹤滩工程，其接入电网均为城市电网，属于重负荷区域，原有短路电流已经接近开关的遮断容量，柔性直流的短路电流贡献需要详细计算。

国内外学者已经对交直流混联电网中直流系统对交流系统的短路电流贡献进行了研究。文献[11]针对三相短路故障，给出了一种基于分段函数的直流系统贡献短路电流的实用计算方法，并指出基于电网换相换流器的高压直流（line commutated converter high voltage direct current，LCC-HVDC）输电只会影响短路电流直流分量。文献[12]针对不对称故障，采用统计分析方法，研究了多种因素对直流短路电流的影响。上述研究均基于LCC-HVDC，由于器件及控制方式的不同，对柔性直流并不完全适用。文献[13]提出了将相间功率控制器和电压源型变换器结合，限制短路电流的方法，但对柔性直流的短路电流原理没有给出具体分析，且在实际工程中也较难实现。文献[14]介绍了在机电仿真软件PSD-BPA中柔性直流短路电流的计算方法，受到机电仿真计算原理的限制，短路电流计算结果偏大，对于运行方式校核偏保守。文献[15]指出柔性直流输电系统贡献的短路电流为同短路点相连的全部VSC换流站贡献的三序短路电流和的叠加，其中正序和负序短路电流受到其电流内环控制器调节可以得到限制，而零序短路电流主要由交流电网和换流变电网侧（Y接侧）等组成的零序网络决定，并基于厦门电网模型得到验证。文献[16-17]分析了三相故障下的模块化多电平换流器高压直流（modular multilevel converter high voltage direct current，MMCHVDC）贡献短路电流的机理，提出了交直流混联系统中柔性直流输电系统贡献短路电流的数学模型和计算方法，但对故障类型分析不全面，同时柔性直流控制系统与工程实际存在偏差[18]。上述文献[14-17]主要针对短路电流的计算方法，对于如何降低故障后换流站两端的短路电流均没有涉及。

本文基于柔性直流输电系统的拓扑结构特征及控制系统特点，分析了柔性直流短路电流的计算机理，对故障后柔性直流贡献短路电流的幅值和相位进行了研究，提出一种降低柔性直流换流站两端公共连接点（point of common coupling，PCC）短路电流的控制策略。基于厦门柔性直流工程，搭建厦门交直流混合电网模型，通过模型仿真结果和实际故障数据对比，验证模型的正确性。在2种控制策略下，仿真对比故障后柔性直流及交流系统的短路电流，证明本文提出的降低柔性直流两端PCC点短路电流策略的正确性及有效性，为后续柔性直流工程并网提供工程经验。

1 柔性直流基本结构和控制方式

1.1 MMC-HVDC基本结构

MMC-HVDC输电技术因易扩展、损耗小、谐波小等优势，已成为柔性直流最常见的拓扑结构。目前，国内的柔性直流工程均采用MMC-HVDC结构，MMC的拓扑结构如图1所示，其中SM为子模块，每个SM包含2个IGBT、2个二极管。

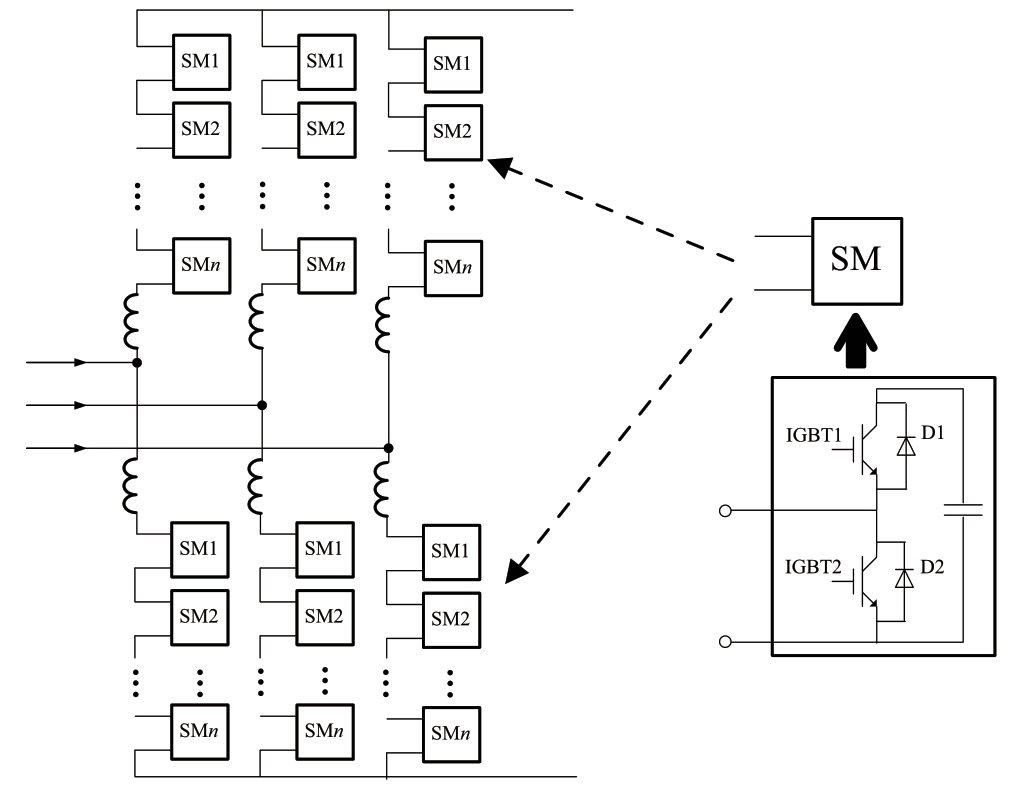
图1 MMC的拓扑结构
Fig.1 Topology of modular multilevel converter

1.2 MMC-HVDC控制方式

工程采用直接电流控制方式对柔性直流进行d、q轴解耦和控制。直接电流控制包含2个控制环节，外环控制和内环控制，外环控制主要为内环控制提供电流参考值；内环控制为电流控制，响应速度快，通过控制换流站的输出电压来快速跟踪电流量的给定。

1.2.1 外环控制

外环控制器的作用是产生内环控制器中交流电流d、q轴分量的参考值idref和iqref，从而达到控制MMCHVDC系统有功功率（直流电压）和无功功率（交流电压）的目的。为了保持系统有功平衡和直流电压稳定，MMC-HVDC系统中必须有一个换流站采用定直流电压控制，而其他换流站可以采用定有功功率控制。

外环控制分为2种，一种是PI控制，根据交流系统中的有功和无功类参数得到内环控制需要的电流参考值；另一种是通过功率公式直接计算出电流参考值。因为整个控制系统中PI环节较多，如仅采用PI控制，参数调节困难，在故障态时会出现响应较慢的情况，而仅采用公式计算又会出现跟踪误差较大的问题，故目前工程通用的外环控制主要采用2种控制方法结合的方式[18]，如图2所示。

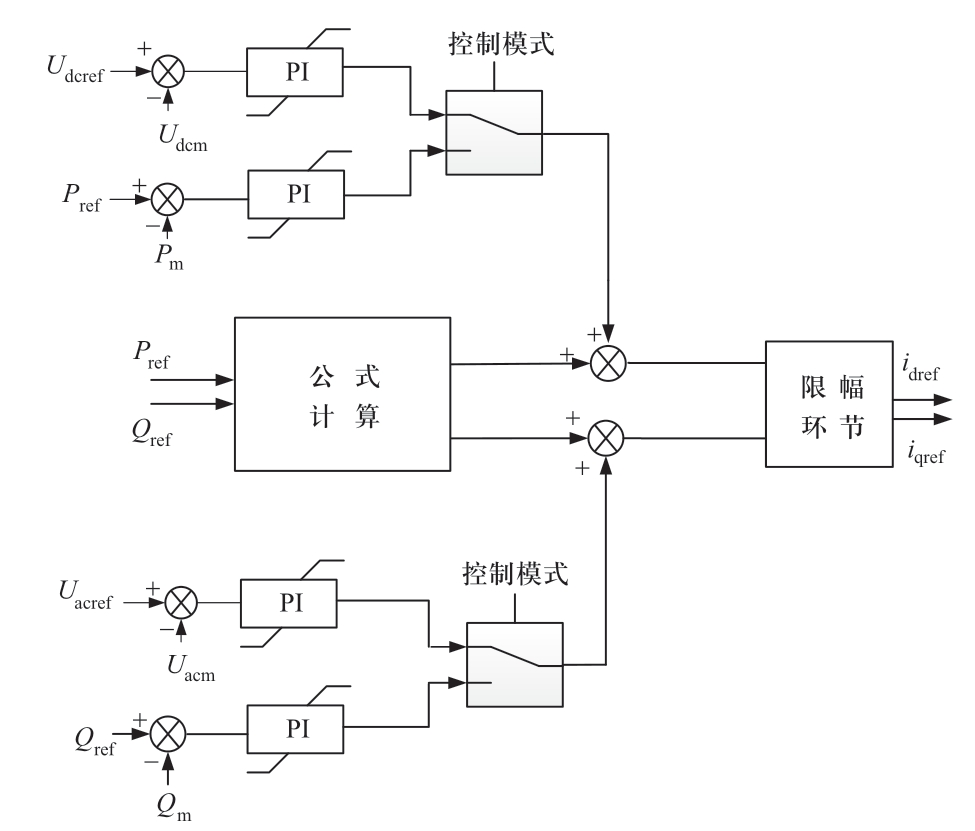
图2 外环控制器模型示意图
Fig.2 Schematic diagram of outer loop controller model

当换流站采用定直流电压控制或定交流电压控制时，可利用PI反馈控制生成相应有功电流或无功电流的参考值，此时Pref和Qref均设置为0。

1.2.2 外环电流限幅

一旦交流系统发生故障，换流站PCC点电压下降，达到相同输出功率的电流设定idref、iqref就会增大，很可能超出换流站的电流承受能力，因此需要对d、q轴电流的设定进行限幅。

根据应用场景的不同，电流限幅可分为有功优先、无功优先或按照设定功率平均分配等。上述限值在维持故障期间功率输送的同时，考虑了半导体器件的安全性，防止过流对换流站设备产生损害。

1.2.3 内环电流控制

内环电流控制前，首先将交流网络中的三相电压电流等参数进行d、q解耦，得到d-q坐标系下的电压、电流值。内环电流控制中，交流电流实际值id、iq与外环控制器输出的交流电流参考值idref、iqref通过比例积分环节得到交流电压参考值udref、uqref。通过调节交流电压参考值，使交流电流跟踪外环控制器计算得到的交流电流参考值。其示意图如图3所示，其中Vp是交流前馈电压值，LC是桥臂电抗电感值。

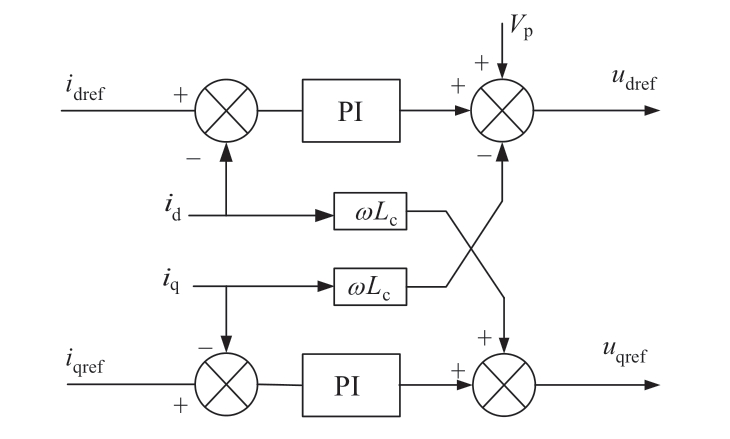
图3 内环控制系统模型示意图
Fig.3 Diagram of inner loop control system model

2 短路电流分析方法

2.1 叠加原理

电网异常工况下，往往要求换流站能够快速实现锁相和对三相电流的控制，从而实现对电网的快速支援，这种控制的实现时间应不超过1～2个周波；又考虑到一般的电网保护是通过交流断路器来实现的，一般断路器的动作延时约60～80 ms，因此换流站对断路器切断容量的影响也处于故障稳态范围，或者说换流站对于电网保护设计的影响处于故障稳态范围[19]。

当交流电网故障进入稳态计算短路电流时，换流站接入系统的组件仅包括变压器和换相电抗，并无非线性元件，系统网络结构具有对称性，可采用叠加原理进行计算。

根据叠加原理可知，PCC点的短路电流由原有交流系统短路电流和柔性直流的短路电流叠加，主要受柔性直流短路电流的大小和相位所影响，其中，短路电流的大小受限幅的限制，在此不做详细研究，主要研究柔性直流短路电流的相位角。

2.2 柔性直流短路电流相位角计算

换流站实际输出的电流移相角度并不是换流站输出电流的实际初始相位，而是其相对于锁相环输出相位的角度，因此，换流站输出电流的实际相位和锁相环所锁定的相位是强相关的。常见的不对称故障下的锁相方法是通过相序分解法对正负序分量进行分解，从而对分解得到的正序分量进行锁相，本文分析中同样认为锁相环在故障下能够快速锁定换流站PCC点母线的正序电压相位。

通常，三相短路电流最大，只需校核三相短路故障。考虑厦门工程换流变的接线方式Y0/Δ，柔性直流换流变网侧为Y型且接地，存在零序通路，因此本文分析单相短路故障和三相短路故障。

对于单相短路故障及三相非金属性接地故障，PCC点仍有正序残压，锁相环可以准确锁相。设定换流站的输出相位以PCC处相位为参考相位，由柔性直流的工作原理可知转换到三相坐标系之后，换流站输出电流为

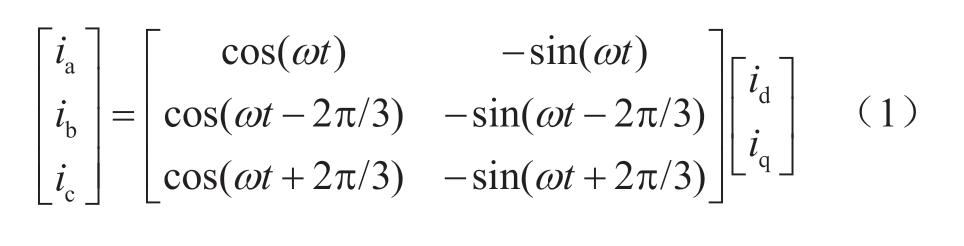
解得三相电流

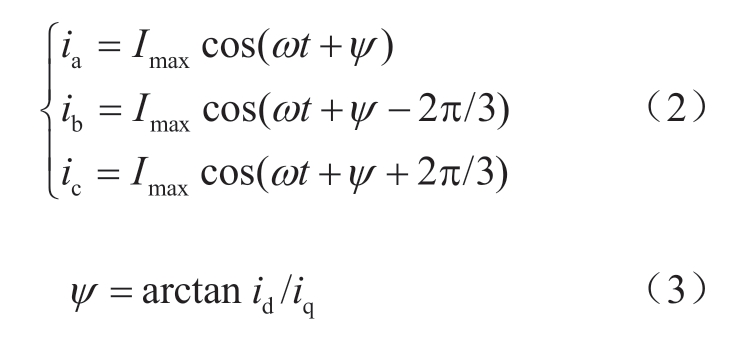
式中：ia、ib、ic是柔性直流向PCC点输出的三相电流；id、iq是转换到d、q轴上的电流值；Imax是电流的幅值；ψ为柔性直流短路电流与PCC处母线电压的夹角[16]。若柔性直流工程无功设定为0时，即q轴分量iq为0，换流站输出电流与PCC点电压方向同向。特殊情况下，当PCC点发生三相短路金属性接地故障时，接地电阻为0，PCC点电压跌落到0，锁相环采集不到正序电压。在厦门柔性直流工程中，设定锁相环会维持故障前PCC点电压相位输出，以保证系统的稳定性。本情况不适用于下文所提出的PCC点短路电流控制策略。

3 柔性直流PCC点短路电流控制策略

3.1 短路电流计算

对于PCC点发生短路后，故障电流的计算可等效为如图4所示。其中，Xeq、Req是交流系统的等值电抗、等值电阻，计及电力网络中各元件的电抗一般远大于电阻，即Xeq>>Req。Us、Uc、δ1、δ2分别是交流系统和PCC点母线电压、相角。考虑到柔直传输的功率和并网交流电压，Us与Uc相位差很小，即δ1≈δ2。对于220 kV及以上交流线路，当PCC点发生三相小电阻接地或者单相接地故障时，基于上述假设，可近似认为故障情况下交流系统对PCC点的注入电流方向滞后PCC点电压90°。

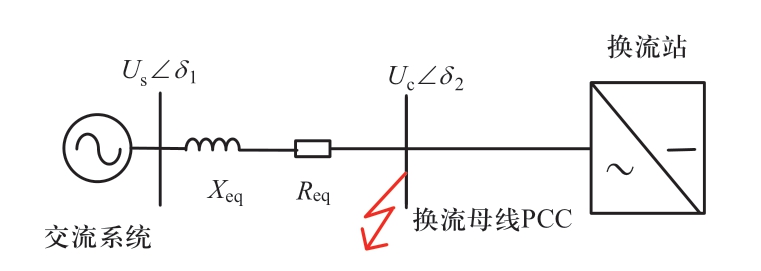
图4 短路电流计算等效示意图
Fig.4 Equivalent schematic diagram of short circuit current calculation

可见，若故障情况下柔性直流只有有功输出，即输出短路电流与PCC点电压同相位，考虑到故障后短路电流的分流，当接地电阻很小时，流入接地点的柔性直流电流与PCC点电压同相位，即柔性直流换流站输出电流与交流系统注入短路点的电流方向相差90°，此时柔性直流对故障点短路电流幅值的影响可忽略不计。若只有无功输出，柔性直流输出电流与交流系统注入短路点的电流同相位，此时柔性直流对故障点短路电流幅值的影响最大。

3.2 短路电流控制策略

通过上述分析可知，故障期间，限制柔性直流的无功输出即可减少PCC点的短路电流。综合考虑故障期间的功率传输及故障后的系统恢复，提出电流限幅与有功优先相结合的策略，使故障期间柔性直流只发送有功，不发送无功。由于城市电网属于强系统，对柔直无功需求较小，采用此策略不会影响系统的电压稳定性。

随着实际工程的投运，发现故障期间减少交直流系统交互的功率，更有利于故障的恢复与系统的稳定，与LCC-HVDC的VDCOL控制有相似之处。结合交流电网实际情况，电流限幅环节的逻辑设计如下，其中Iref是电流幅值参考值：

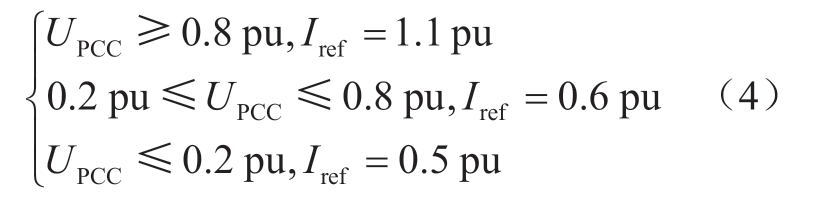
考虑到近区单相接地故障和三相接地故障时系统电压的跌落幅度，故PCC点电压有效值设定为0.8 pu和0.2 pu，电流参考值的设定可根据不同电网特性进行调整。对于强电网，无功需求较弱，同时短路电流较大，可降低电流的参考值。弱电网则反之。

故障期间有功优先策略如下：q轴电流的上限，可以按d轴电流设定值与总电流限制之间的裕度来确定。例如当d轴电流设定超出上限时，q轴电流设定为0；d轴电流设定为0时，q轴电流的设定上限为最大电流限值，其关系为

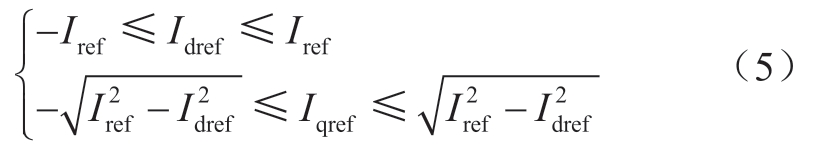
将上述2个策略结合，具有如下优点：①PCC点发生严重故障，电压跌落达到限值时，柔性直流无功电流输出设定为0，在保证有功输出的同时，减少了PCC点短路电流；②稳态情况下，不影响系统正常运行。

3.3 PCC点短路电流特性分析

柔性直流并网PCC点，需考虑单相短路故障。由短路电流国家标准及IEC 60909可知，单相短路故障时，短路电流交流分量初始值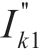按照式（6）计算：

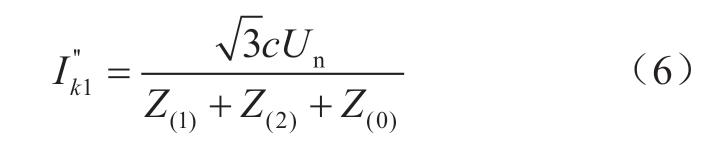
式中：c为电压系数，通常取1；Un是系统标称电压；Z(1)、Z(2)、Z(0)分别是系统的正序阻抗、负序阻抗、零序阻抗。

若考虑 Z(1)=Z(2)，则电流绝对值计算如式 （7）：

三相短路故障时，只有正序分量。采用等效电压源和短路阻抗Z(1)，通过式（8）计算对称短路电流初始值。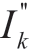

可知，当在PCC处发生短路时，由于换流变网侧为Y型接线，存在零序回路，若Z(0)＜ Z(1)=Z(2)，则单相短路电流将大于三相短路电流，与后续仿真结果一致。

4 仿真模型

4.1 模型介绍

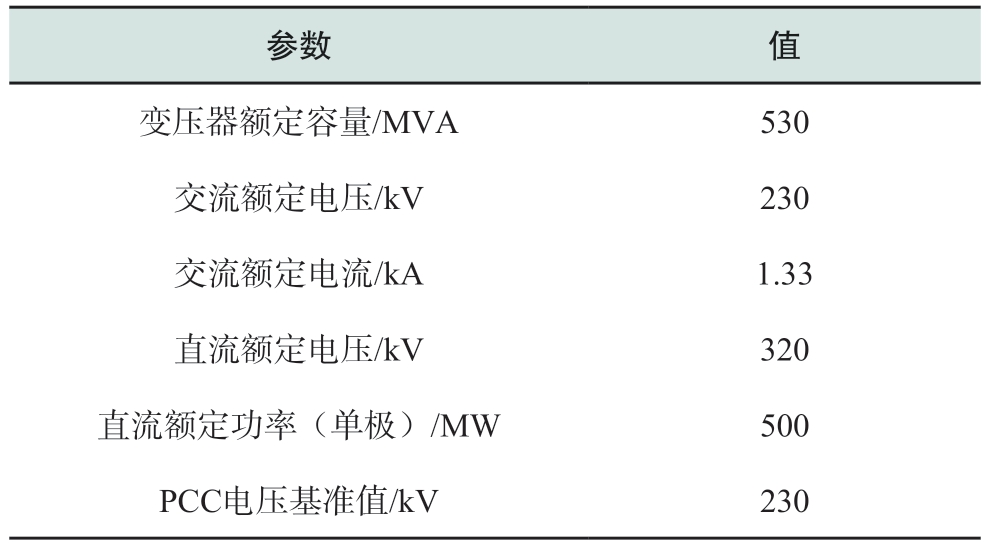
开发双端双极±320 kV/1000 MW厦门柔性直流工程详细的PSCAD电磁暂态仿真模型，参数如表1所示。直流线路为按照工程参数搭建的直流电缆。该模型送端采用定有功功率控制策略、受端采用定直流电压控制策略，通过测量交流系统电压、电流、有功功率和无功功率，直流线路电压、电流等电气量，完成对换流站的有功、无功及电压控制，配合一系列断路器的时间投退连锁逻辑，实现柔性直流模型的全自动解闭锁及稳态运行。

表1 直流模型参数（单极）
Table 1 DC model parameter (monopole)

交流系统采用等值电网，将原有系统的6432个节点、538台发电机、5955条支路等值为42个节点、8台发电机和79条支路。保留了厦门市内220 kV及以上全部交流系统，考虑到海沧和东岗为等值边界，且功率传输较大，故设置为等值机，等值电网如图5所示[20]。柔性直流并入等值后的交流电网，其控制保护系统与实际工程一致。

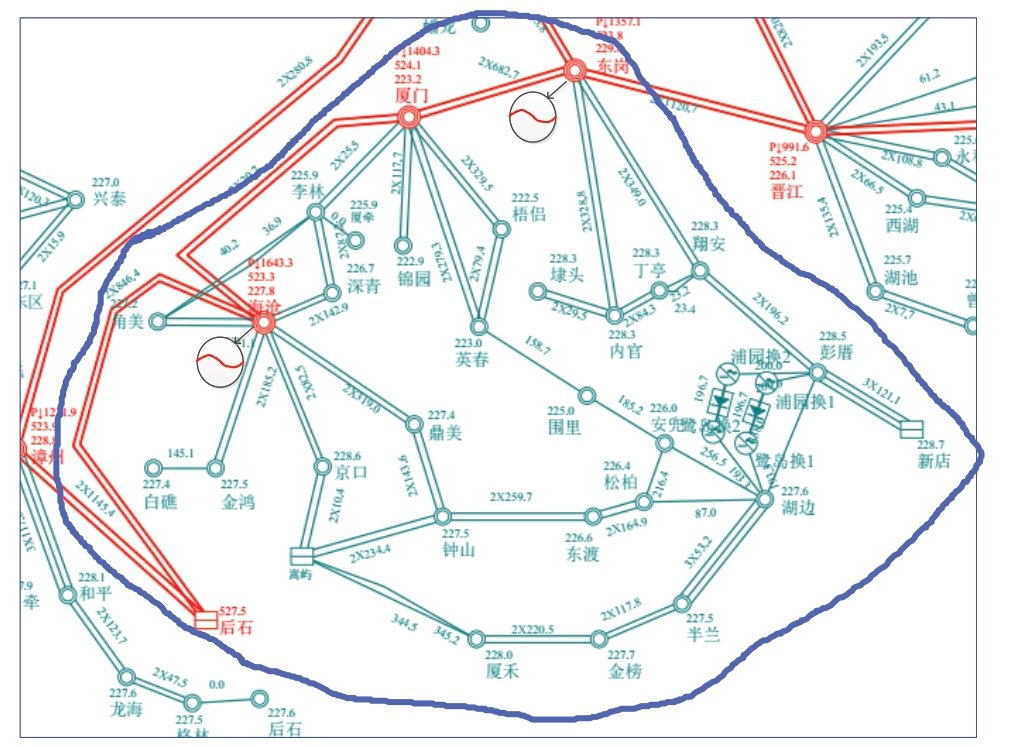
图5 交流系统等值电网
Fig.5 Equivalent grid of AC system

4.2 模型校验

根据国网福建电力科学研究院提供的报告[21]及电网运行数据，对开发的混合系统模型进行校验。按照报告的运行方式相应调整柔性直流运行方式，柔性直流单极180 MW运行，新店2#停机。海沧220 kV母线发生A相接地故障时，仿真波形如图6所示。

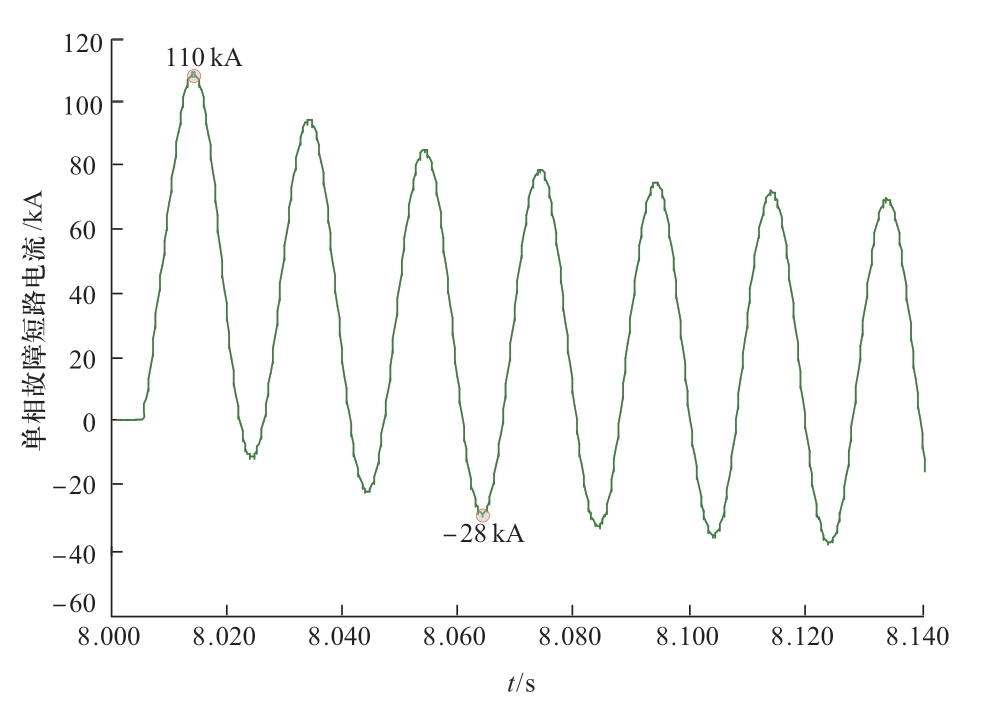
图6 闵海沧220 kV母线单相故障仿真波形
Fig.6 Single phase fault simulation waveform of Minhaicang 220 kV bus

如图6所示，故障后3个周波内从220 kV母线流过故障点最大短路电流正幅值为110 kA，负幅值为28 kA，与报告内计算短路电流的方法一致，可得有效值为48.80 kA，计算结果与报告数据48 kA相比误差仅为1.7%，验证了仿真模型的准确性。

5 仿真验证

为了更直观地展现换流站并入电网后提供的短路电流及其控制策略，下面以PCC点湖边为例，分别对2种控制策略的情况进行仿真，计算短路电流。湖边母线发生短路故障情况如图7所示，其中I1、I2、I3分别为交流系统各相连支路或等效支路的馈入短路电流，I4为柔性直流馈入的短路电流。

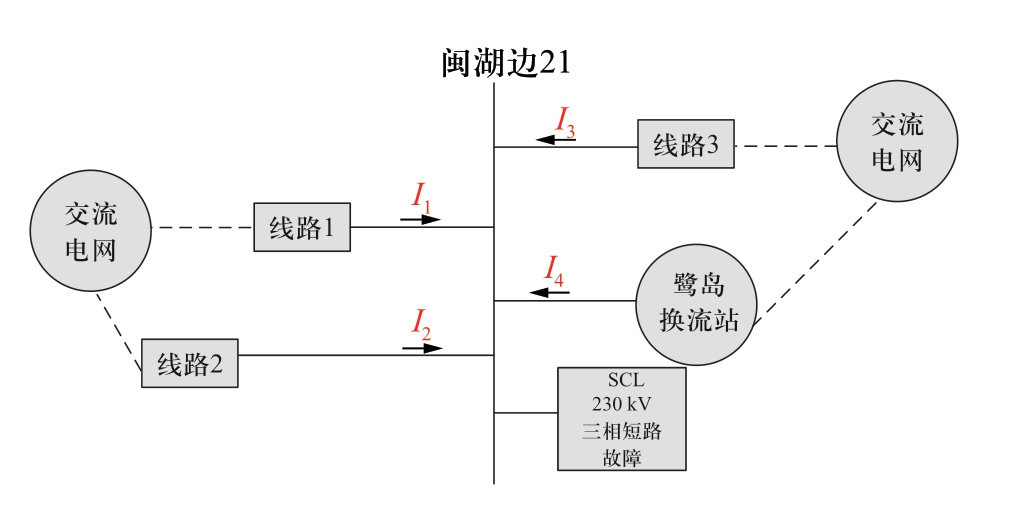
图7 湖边母线短路电流示意图
Fig.7 Short-circuit current diagram of Hubian bus

因模型较大，涉及到发电机并网，系统大约在7 s左右后进入稳态。设置三相短路故障，短路电阻为0.01 Ω，保证了锁相环可正常工作。故障开始时间设置在8 s，故障时A相电压角度a=0°，故障持续时间0.15 s。根据电网的实际运行方式，厦门鹭岛换流站定直流电压1.0 pu、定无功200 Mvar；浦园换流站定有功400 MW，定无功200 Mvar。

5.1 三相故障

5.1.1 无功优先策略

由于厦门电网网架较强，短路电流已接近遮断容量。柔直工程在故障期间输出的短路电流，与电网原有的短路电流相比，占比仅5.2%左右，故为了对比明显，且验证上述无功功率对故障点短路电流的贡献，控制系统采用了无功优先的方式，即在故障期间，柔性直流有功电流参考值idref设为0。

无功优先策略下，湖边230 kV母线三相故障仿真波形如图8所示。从图8 （a）可以看出，故障50 ms后，有功功率、无功功率均跌落接近到0 MW，符合实际工况。由图8（b）看出，大约在8.015 s，电压跌落到0.8 pu，电流限幅值0.6 pu，电压继续跌落，在8.027 s时，电压跌落到0.2 pu，电流限幅值0.5 pu，之后电压恢复后，电流限幅值随之增大，待故障消失后，电流限幅值恢复到稳态值。图8 （c）是外环输出的有功和无功的电流参考值，故障期间有功电流参考值idref为0。

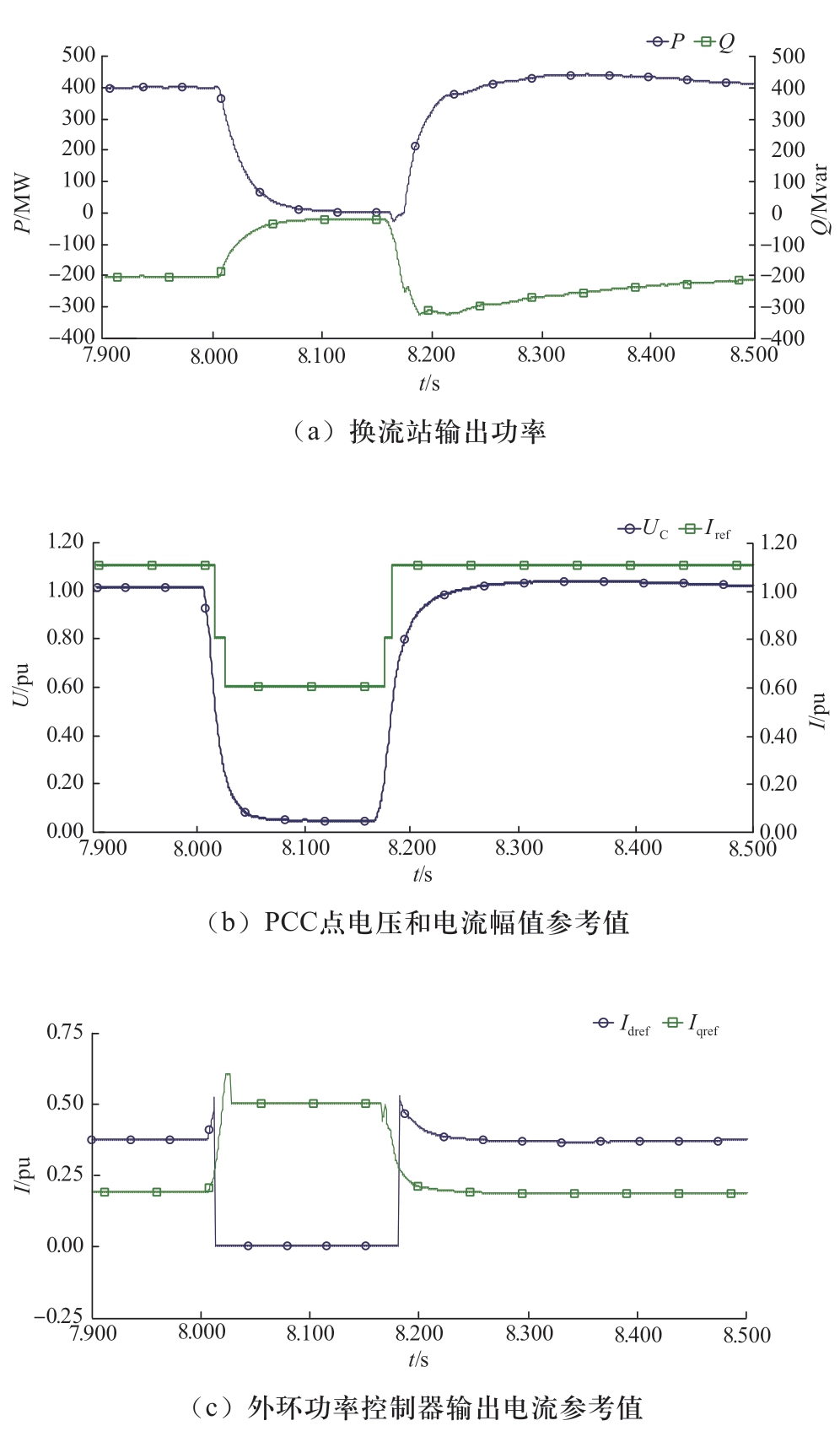
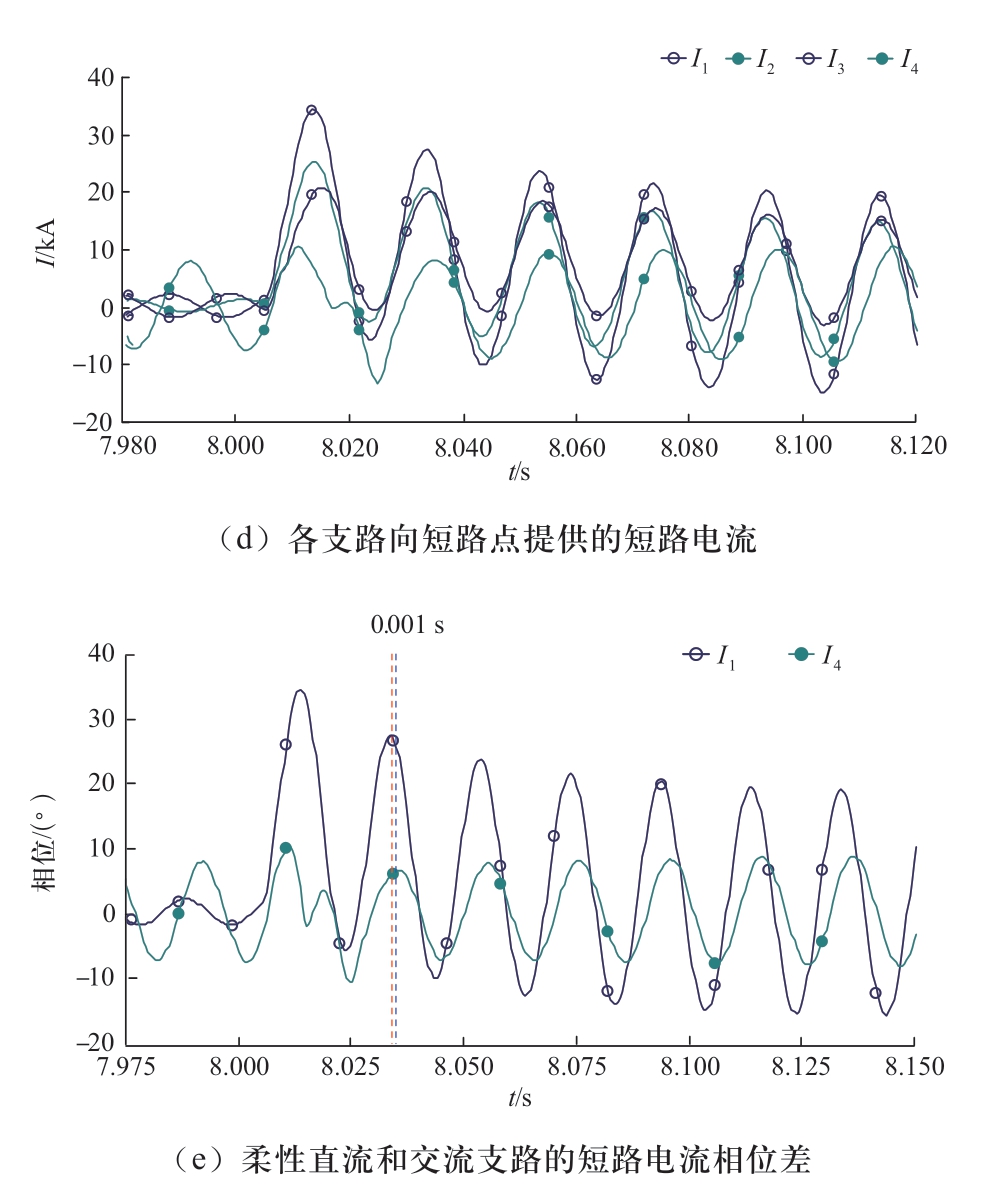
图8 湖边230 kV母线三相故障仿真波形（无功优先策略）
Fig.8 Simulation waveform of Hubian 230 kV bus three phase fault (reactive power priority strategy)

对于220 kV交流断路器，系统要求120 ms内必须切除故障，实际上在60 ms左右，断路器就会动作切除故障。由图8 （e）可以看出，故障后30 ms～80 ms，柔性直流无功电流的相位与交流系统的电流相位相差较小，粗略认为幅值可以叠加，故在断路器动作期间，满足上述分析。

对于含多条支路的交流系统，故障前，根据系统阻抗特性，稳态电流相位各不相同。故障后，交流系统阻抗特性发生变化，各交流支路向故障点注入短路电流相位较接近，与稳态差别较大，如图8 （d）所示。

5.1.2 短路电流控制策略

运行方式同5.1.1节所述，同时采用短路电流控制策略，故障后系统的响应情况如图9所示。

由图9（a）可以看出，故障期间，柔性直流无功电流参考值iqref为0，设定只发有功。由图9（c）横轴时间上看柔性直流电流的相位与交流系统的电流相位相差大约5 ms（90°），与上述分析一致。

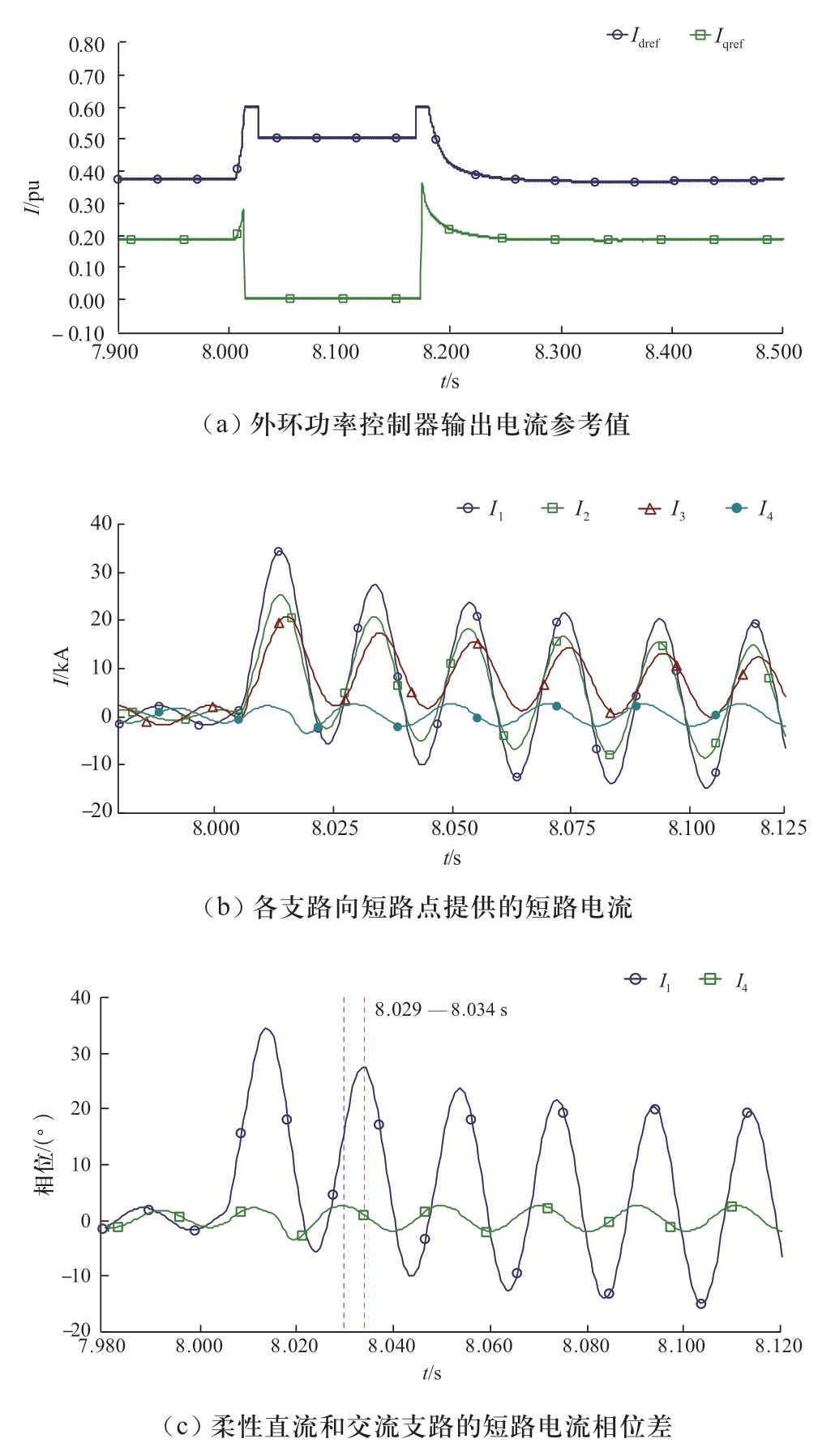
图9 湖边230 kV母线三相故障仿真波形（短路电流控制策略）
Fig.9 Simulation waveform of Hubian 230 kV bus three phase fault (short-circuit control strategy)

在图10 （a）—（c）中，ia1、ib1、ic1为采用无功优先的故障点短路电流，ia、ib、ic为采用短路电流控制策略后的故障点短路电流。采用控制策略后，故障期间故障点的三相短路电流均有所下降，降低的幅值最大可达3.0 kA左右。可见，控制策略可以有效降低故障期间PCC点的短路电流水平。

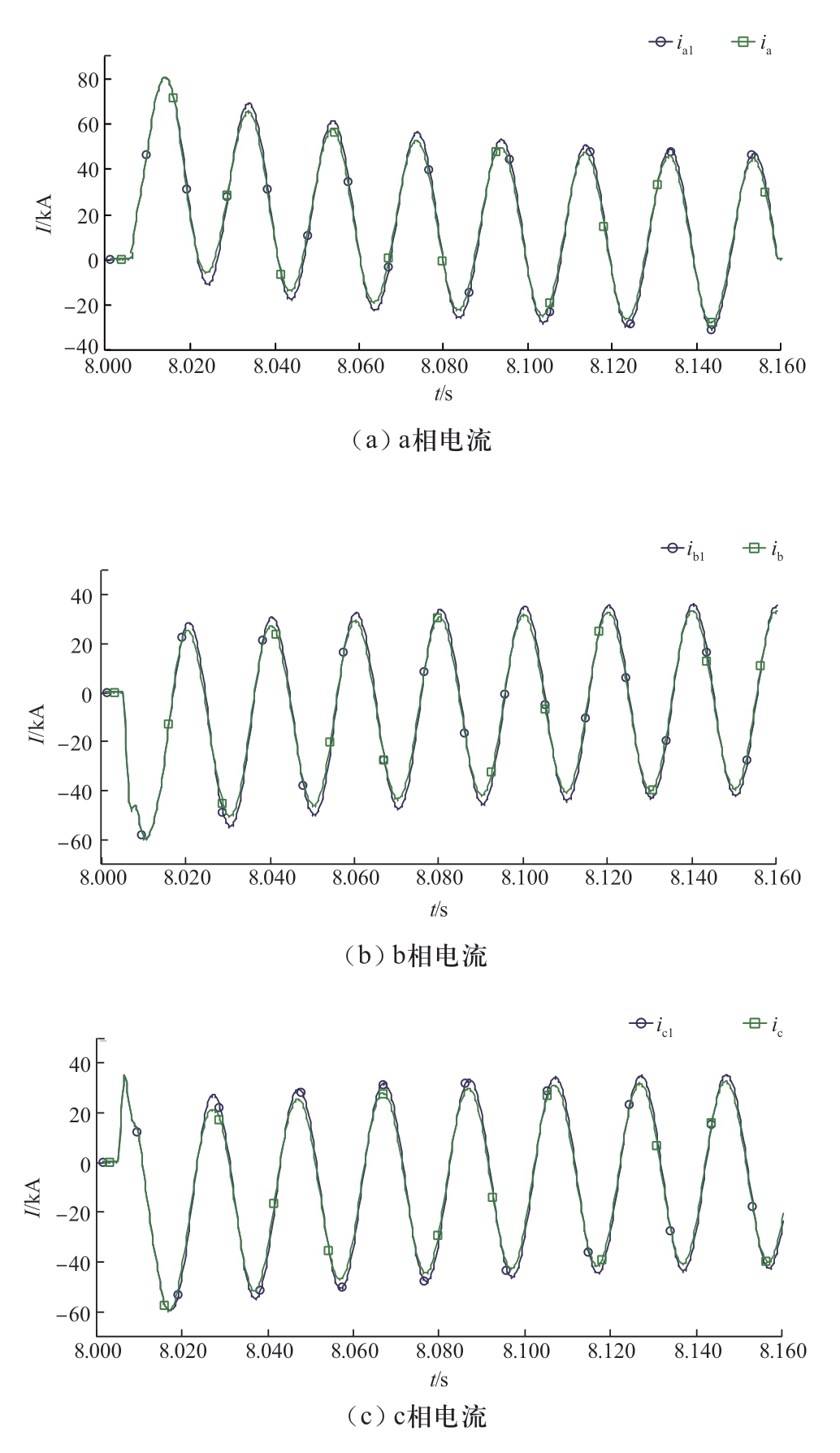
图10 2种控制策略电流波形对比
Fig.10 Comparison of current waveforms with two control strategies

5.2 单相接地故障

由于厦门柔性直流工程网侧换流变采用Y型接地方式，故对PCC点单相接地故障进行校核。运行方式与5.1节相同，均不用控制策略。

图11中ia-3为无控制策略的三相接地故障的短路电流，ia-1为无控制策略的单相接地故障的短路电流。由图11可以看出，在柔性直流近区PCC点发生短路故障时，由于柔性直流换流变接地方式的原因，存在单相接地故障短路电流大于三相接地故障的情况，故在后续工程中，需要对单相接地故障的短路电流进行重点校核。

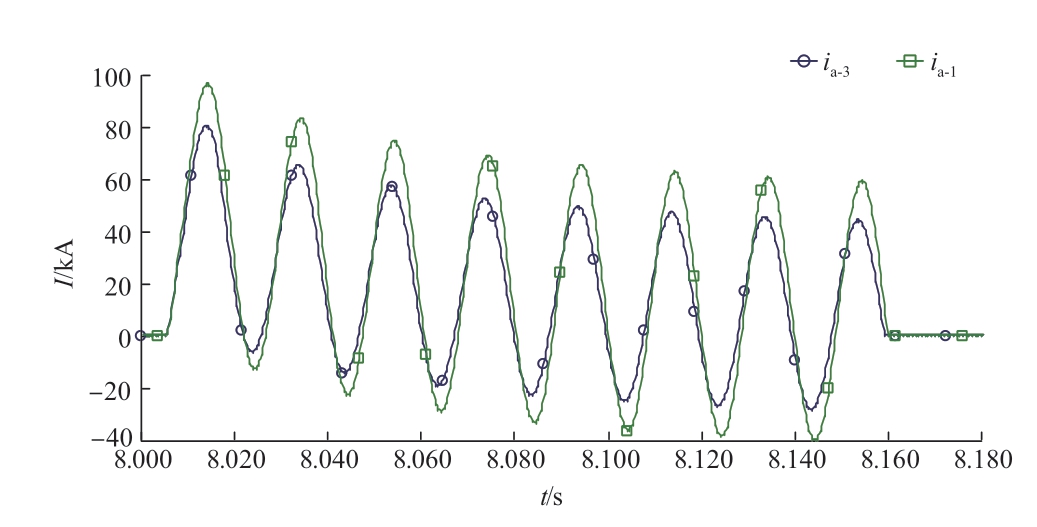
图11 不同故障类型波形对比
Fig.11 Waveform comparison of different fault types

对有无控制策略的PCC点单相接地故障分别进行仿真，验证上述策略的有效性。

图12中，ia1-1为无控制策略的故障点短路电流，ia1为采用控制策略后的故障点短路电流。采用控制策略后，故障相短路电流有所下降，降低的幅值最大可达2.2 kA左右。可见，控制策略可以有效降低单相接地故障期间PCC点的短路电流水平。

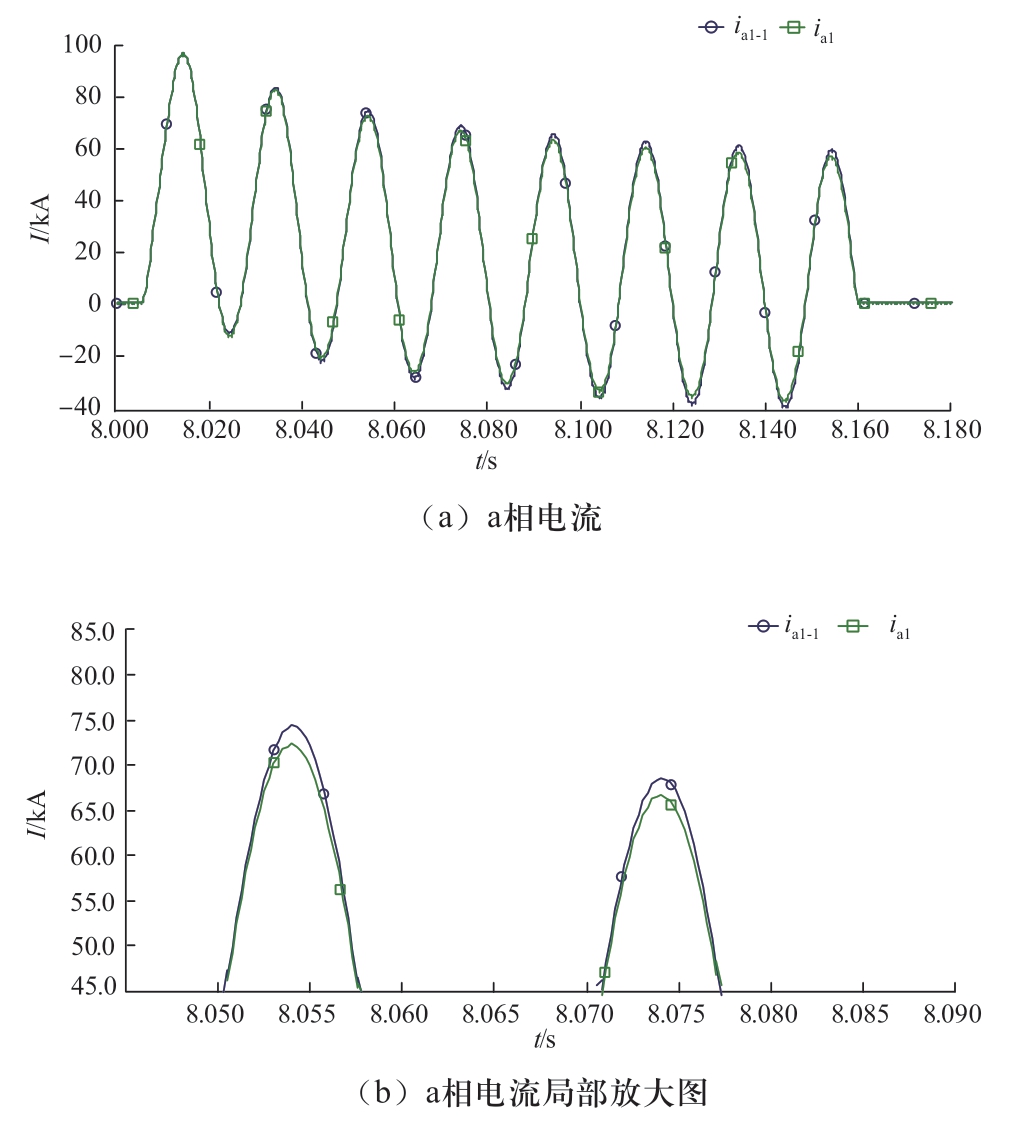
图12 有无控制策略电流波形对比（单相故障）
Fig.12 Comparison of current waveforms with or without control strategy（single phase fault）

6 结论

本文首先对柔性直流提供的短路电流大小和相位进行了机理分析，开发了含厦门柔性直流工程的交直流混合电网电磁暂态模型，提出了一种降低柔性直流两端PCC点短路电流的控制策略，并基于模型进行仿真计算，结果表明：

1）换流站输出电压、电流相位以PCC点电压相位为基准，通过换流站输出有功短路电流与无功短路电流幅值相比，可得到换流站输出短路电流在基准相位下的相角值。

2）故障期间限制柔性直流的无功输出即可减少系统的短路电流。综合考虑故障期间的功率传输及故障后的系统恢复，提出电流限幅与有功优先结合的策略。所提出的控制策略稳态时不影响系统运行，故障期间可降低柔性直流两端PCC点的短路电流。

3）对于PCC点为Y型接线变压器，相同故障点、故障时间，单相故障短路电流值大于三相故障短路电流，短路电流校核时需注意。

4）本文所提策略的控制参数，可根据不同电网特性和故障类型进行相应调整，以满足相应系统安全稳定的需求。

参考文献

[1] 汤广福.基于电压源换流器的高压直流输电技术[M].北京：中国电力出版社，2010: 72-76.TANG Guangfu.High voltage direct current transmission technology based on voltage source converter[M].Beijing:China Electric Power Press, 2010: 72-76(in Chinese).

[2] 汤广福，贺之渊，庞辉.柔性直流输电工程技术研究、应用及发展[J].电力系统自动化，2013，37(15)：3-14.TANG Guangfu, HE Zhiyuan, PANG Hui.Research,application and development of VSC-HVDC engineering technology[J].Automation of Electric Power Systems, 2013,37(15): 3-14(in Chinese).

[3] 汤广福，罗湘，魏晓光.多端直流输电与直流电网技术[J].中国电机工程学报，2013，33(10)：8-17.TANG Guangfu, LUO Xiang, WEI Xiaoguang.Multi-terminal HVDC and DC-grid technology[J].Proceedings of the CSEE,2013, 33(10): 8-17(in Chinese).

[4] 贺之渊，刘栋，庞辉.柔性直流与直流电网仿真技术研究[J].电网技术，2018，42(1)：1-12.HE Zhiyuan, LIU Dong, PANG Hui.Research of simulation technologies of VSC-HVDC and DC grids[J].Power System Technology, 2018, 42(1): 1-12(in Chinese).

[5] 唐溢，李保宏，曾蕊，等.柔性直流对交流系统短路电流影响因素分析[J].电力工程技术，2022，41(1)：40-47.TANG Yi, LI Baohong, ZENG Rui, et al.Influence of VSCHVDC on short-circuit current of AC system[J].Electric Power Engineering Technology, 2022, 41(1): 40-47(in Chinese).

[6] 张成泉，邹贵彬，张烁，等.适用于多端柔性直流电网的潮流控制器[J].电力系统保护与控制，2022，50(20)：32-40.ZHANG Chengquan, ZOU Guibin, ZHANG Shuo, et al.A current flow controller suitable for MTDC grids[J].Power System Protection and Control, 2022, 50(20): 32-40(in Chinese).

[7] HE J H, CHEN K A, LI M, et al.Active injection protection scheme for flexible HVDC grids based on amplitude of input impedance[J].Global Energy Interconnection, 2021, 4(6): 532-542.

[8] 李国庆，徐亚男，江守其，等.海上风电经柔性直流联网系统受端交流故障穿越协调控制策略[J].电力系统保护与控制，2022，50(7)：111-119.LI Guoqing, XU Yanan, JIANG Shouqi, et al.Coordinated control strategy for receiving-end AC fault ride-through of an MMC-HVDC connecting offshore wind power[J].Power System Protection and Control, 2022, 50(7): 111-119(in Chinese).

[9] 高凯，阳岳希，张艳军，等.适用于城市电网的柔性环网控制器拓扑方案研究[J].电网技术，2016，40(1)：78-85.GAO Kai, YANG Yuexi, ZHANG Yanjun, et al.A topology research of flexible looped network controller suitable to urban power grid[J].Power System Technology, 2016, 40(1): 78-85(in Chinese).

[10] WASSERRAB A, BALZER G, MÜLLER H, et al.Shortcircuit calculation in AC networks in case of HVDC stations[C]//CIGRÉ Winnipeg 2017 Colloquium A3, B4 & D1,Winnipeg, Canada, Sep.30-Oct.06, 2017.

[11] 王铁柱，万磊，卜广全，等.逆变侧交流系统三相短路时直流系统贡献短路电流的机理和计算方法研究[J].电网技术，2016，40(5)：1313-1319.WANG Tiezhu, WAN Lei, BU Guangquan, et al.Mechanism and calculation method study of DC system contributed shortcircuit current with three-phase short-circuit fault on inverter side[J].Power System Technology, 2016, 40(5): 1313-1319(in Chinese).

[12] 王铁柱，万磊，张彦涛，等.交流侧单相短路时直流系统提供短路电流的特性分析[J].电网技术，2016，40(7)：1970-1977.WANG Tiezhu, WAN Lei, ZHANG Yantao, et al.A study of characteristic of short-circuit current contributed by DC systems with single-phase short-circuit fault on AC side[J].Power System Technology, 2016, 40(7): 1970-1977(in Chinese).

[13] 李娟，严宇昕，聂鹏.基于VSC的DCIPC阻尼系统功率振荡及限制短路电流研究[J].电力自动化设备，2015，35(5)：58-63.LI Juan, YAN Yuxin, NIE Peng.Power oscillation damping and short circuit current limiting by VSC-based DCIPC[J].Electric Power Automation Equipment, 2015, 35(5): 58-63(in Chinese).

[14] 李英彪.柔性直流电网故障特性及其控制策略研究[D].北京：中国电力科学研究院，2017.

[15] 易杨，沈豫，林章岁.柔性直流输电系统贡献交流短路电流的特性分析及计算方法[J].高电压技术，2018，44(7)：2150-2158.YI Yang, SHEN Yu, LIN Zhangsui.Characteristics and analysis methods of AC short-circuit current contributed by VSC-HVDC[J].High Voltage Engineering, 2018, 44(7): 2150-2158(in Chinese).

[16] 卜广全，李英彪，王姗姗，等.MMC对交流系统三相短路故障短路电流影响的机理研究[J].中国电机工程学报，2017, 37(21)：6303-6312.BU Guangquan, LI Yingbiao, WANG Shanshan, et al.Analysis of the short-circuit current of MMC-HVDC[J].Proceedings of the CSEE, 2017, 37(21): 6303-6312(in Chinese).

[17] 李英彪，李轶群，秦善萌，等.柔性直流输电换流站输出短路电流水平机理分析[J].全球能源互联网，2019，2(6)：581-588.LI Yingbiao, LI Yiqun, QIN Shanmeng, et al.Study on the effect of VSC–HVDC on converter output short circuit current level[J].Journal of Global Energy Interconnection, 2019, 2(6):581-588(in Chinese).

[18] 郭贤珊，刘斌，梅红明，等.渝鄂直流背靠背联网工程交直流系统谐振分析与抑制[J].电力系统自动化，2020，44(20)：157-164.GUO Xianshan, LIU Bin, MEI Hongming, et al.Analysis and suppression of resonance between AC and DC systems in Chongqing-Hubei back-to-back HVDC project of China[J].Automation of Electric Power Systems, 2020, 44(20): 157-164(in Chinese).

[19] 杨杰.电压源换相高压直流输电交直流系统故障特性研究[D].北京：清华大学，2010.

[20] 朱琳，葛俊，吴学光，等.一种工程实用的电力系统等值方法[J].电力自动化设备，2017，37(9)：178-184.ZHU Lin, GE Jun, WU Xueguang, et al.Power system equivalence for practical engineering[J].Electric Power Automation Equipment, 2017, 37(9): 178-184(in Chinese).

[21] 国网福建电力科学研究院.500 kV海沧变#4联变220 kV侧26D开关间隔A相出线套管气室放电故障抢修过程及故障分析报告[R].福州：国网福建电力科学研究院，2018.

Study on the Influence of VSC-HVDC into Urban Power Grid on Short-circuit Current of the Adjacent Area of Converter Station

ZHU Lin1,2*, KOU Longze1,2, FAN Zheng1, GU Huaiguang1,2
(1.State Key Laboratory of Advanced Power Transmission Technology, State Grid Smart Grid Research Institute Co., Ltd.,Changping District, Beijing 102209, China;2.Beijing Key Laboratory of DC Grid Technology & Simulation, State Grid Smart Grid Research Institute Co., Ltd.,Changping District, Beijing 102209, China)

Abstract: The short-circuit current of large-scale urban power supply grid is approaching the breaking capacity of circuit breaker.After the connection of VSC-HVDC transmission system, the working current will be provided during the fault,resulting in the short-circuit current exceeding the standard of AC system, and the limitation of VSC-HVDC transmission power.In this paper, based on the control method of VSCHVDC inner and outer loop and the calculation principle of short-circuit current in AC system, it is concluded that the amplitude and phase of short-circuit current of VSC-HVDC transmission system have great influence on the short-circuit current at the connecting point.And, the amplitude of shortcircuit current is easy to control, because it’s affected by the current limiting.Therefore, it is of great necessity to focus in the control of phase.Based on this, a control method is proposed to reduce the short-circuit currents at both ends of the VSCHVDC converter station.Taking the actual Xiamen project as an example, a hybrid AC/DC model is built, and the correctness of the model is verified by comparing with the measured waveform.And then the validity and correctness of the proposed method are verified, by which the short-circuit current at the connection point is effectively reduced.

Keywords: VSC-HVDC; short-circuit current; amplitude limiting control; fault type; Xiamen VSC-HVDC project

作者简介：

朱琳

朱琳（1986），女，硕士，高级工程师，从事电力系统及柔性直流仿真技术研究。通信作者，E-mail：zhulin@geiri.sgcc.com.cn。

寇龙泽（1989），男，硕士，高级工程师，从事柔性直流控制保护仿真研究，E-mail：koulongze@geiri.sgcc.com.cn。

范征（1983），男，硕士，高级工程师，从事电力系统电磁暂态建模与仿真，E-mail：fanzheng@geiri.sgcc.com.cn。

谷怀广（1986），男，硕士，工程师，从事柔性直流动模仿真研究，E-mail：guhuaiguang@geiri.sgcc.com.cn。

（责任编辑 李锡）