0 引言
随着能源互联网的建设和发展,配电网中不断接入各类电源,如热电联产机组、微型燃气轮机等可控分布式电源,以及风电和光伏等可再生能源发电(variable renewable energy-distributed generation,VREDG),使配电网在极端情况下利用本地电源实现应急供电恢复成为可能[1]。然而配电网中本地可控电源存储的燃料或电量有限,而VRE-DG在天气条件良好的情况下出力可观,能够为配电网应急供电恢复提供有力支撑。
已有学者对极端事件引发大停电场景下利用配电网本地电源实现应急供电恢复开展研究。在初期研究中,通常将该问题建模为单时间断面的优化问题[2-4],得到的解为单时间断面的恢复状态。然而,因极端事件导致的停电时间可长达数小时甚至数天,而本地可控电源(如储能或独立的燃料发电机等)存储的电量或燃料有限,在极端情况下可能无法及时补给,求解得到的单时间断面恢复策略到恢复后期会由于电源退出运行而无法适用。此外,恢复过程中随着修复工作的推进,系统状态(拓扑可用状态、负荷状态和发电资源可用状态)也可能发生变化,且VRE-DG的输出功率也随时间波动,因此很多学者在恢复问题建模时计及时间维度,考虑发电资源稀缺性,保证能量在时间维度的优化配置[5-8]。
文章[8]提出一种考虑负荷重要性与源-荷互补性的负荷恢复策略。文章[9]以最大化为负荷供电的累积加权时间为目标,考虑了微电网可以向配电网供给的电量约束。文章[10-13]将停电时间平均划分为若干时段,考虑恢复过程中可能存在的拓扑变化,将问题建模为混合整数线性规划问题,直接利用成熟优化求解器求解,以优化发电资源在时间维度的分配,提升应急供电恢复的效果。以上文章探索了极端事件引发停电事故后发电资源稀缺问题的解决方案,但如何在时空维度协同不用类型电源实现能量最优配置仍有待进一步探索。
利用VRE-DG辅助恢复需要考虑其出力的不确定性。处理恢复问题中可再生能源输出功率不确定性的方法主要有3种:随机规划方法[9,13-16]、鲁棒优化方法[17-18]和预测值替代实际出力值方法[12,19]。其中,随机规划方法是在给定约束条件成立概率满足一定置信水平的条件下对目标期望值的优化,分为基于场景采样的方法[9,13]和基于概率密度函数的数学规划方法[14-15]。前者需采样相当多场景确保准确性导致计算量大,后者较难获取精确的概率分布函数,均具有一定局限性。鲁棒优化方法不需要已知随机量的概率分布,只需获得随机量参数的区间范围,但该方法由于无法充分利用可获取的概率统计信息而使所得的优化解过于保守。第三种是利用预测值替代实际出力值。如文献[12]和[19]中,即是用可再生能源短期预测值替代实际处理值,将恢复问题建模为确定性优化问题,具有一定实用价值。可见,3种方法均有各自特点。值得强调的是,在供电恢复中,生成的电气孤岛并无大电网支撑,选取的VRE-DG不确定性处理策略应尽量避免功率失衡引发关键负荷的二次断电甚至恢复失败,减小次生损失。
综上所述,考虑到极端事件引发大停电事件后发电资源的稀缺性,需要在时空维度实现有限发电资源的优化配置,且利用VRE-DG时需要尽可能降低其出力不确定性带来的风险,避免重要负荷二次断电或恢复失败事故发生。
1 考虑VRE-DG的应急供电恢复策略基本原理
假设大停电事故后,所有负荷均处于停电状态,且所有的故障已被隔离,此时重要电力用户靠电储能系统、柴油机等确定性、可控备用电源紧急供电,但受容量或燃料限制,备用电源供电时间和范围有限。当配电网内有其他分布式发电时,可以将未隔离的可连接线路尽量相连,形成多个尽可能大的孤岛[20],利用各孤岛内所有应急备用电源、分布式发电(包括不确定性的风、光发电和确定性的储能、小型燃机等),保证重要负荷供电时间,同时扩大恢复供电范围。
考虑到分布式发电中有大量不确定性的风、光发电,需要避免发生因乐观估计其出力、恢复过多负荷,而使得确定性发电设备和应急电源的能量无法保证重要负荷供电的情况。另外,由于在孤岛运行系统薄弱,VRE-DG或负荷波动过大时可能导致功率失衡、引发切负荷等操作,影响极其恶劣,在恢复过程中应尽力避免。因此,应急供电恢复策略应采取保守原则,首先确保重要负荷备用时间,其次充分利用VER发电能力。
本文提出的各孤岛的多时段滚动修正恢复策略原理如图1所示。将停电后至输电网送电通路恢复前的时长T0划分为若干时段,每个时段长度为Tint,所有时段构成的集合定义为T。其中,T0可由调度人员凭借经验,根据灾害类型、影响范围、气象局和地震局等外部信息以及大电网恢复进程等评估得到。
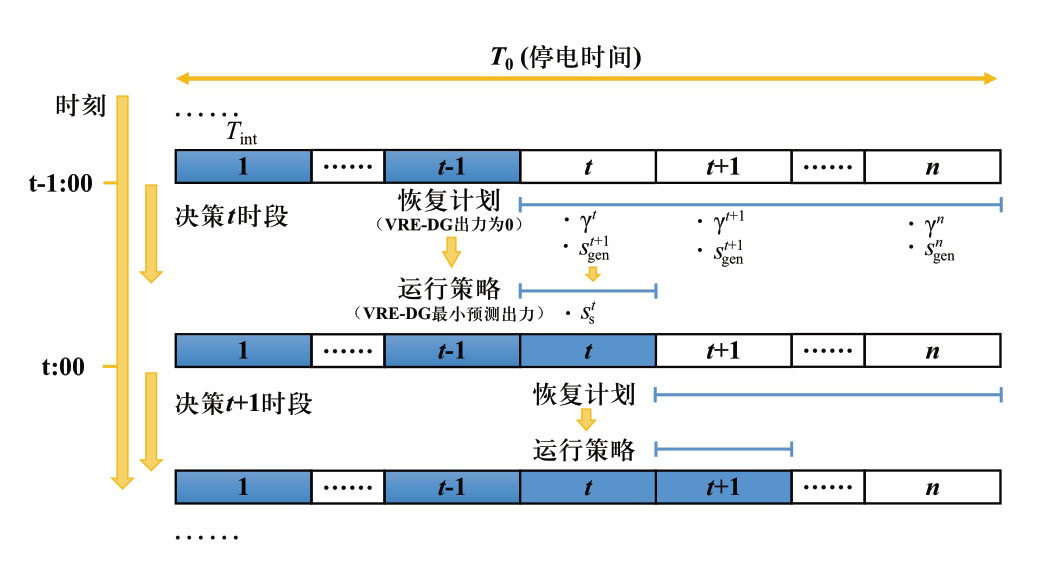
图1 基于滚动修正的配电网应急供电恢复策略示意图
Fig.1 Diagram of power supply restoration strategy based on rolling plan
在t-1时刻,为了最大程度降低VRE-DG输出功率不确定带来的风险,假设其出力为0,考虑以后所有时段运行计划,求解多时段恢复优化决策模型(MPCLR),确定t 时段计划恢复负荷集合以及各可控电源的计划输出功率。然后,根据VRE-DG在该时段的最小预测出力,求解优化运行模型(OP),制定该时段的优化运行策略,充分利用VRE-DG供电。
2 多时段恢复计划优化决策模型
2.1 问题描述
多源协同的配电网多时段恢复计划优化决策模型用于决定当前时段及其后面时段的恢复计划。决策变量为各个时段各个电源出力值、各个时段负荷恢复状态以及线路开关状态。目标函数是最大化加权负荷供电时间。需要考虑的约束条件包括潮流约束、电压约束和电流约束,辐射状约束、负荷自备应急电源的自备时间约束、配电网内可控电源能量约束、储能设备的SOC约束、负荷状态变化约束等。
2.2 多时段恢复计划优化决策的线性模型
在每个时段初期,需要修正当前时段及其后所有时段的恢复计划。本文假设当前时段及其后所有时段构成的集合为T ′,针对每个孤岛可建立MPCLR-milp模型如下:
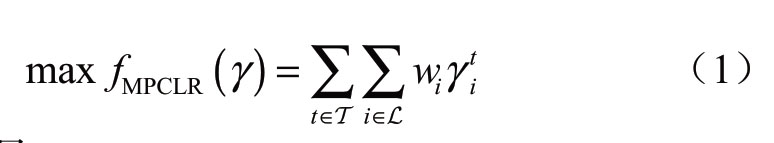
其中变量:
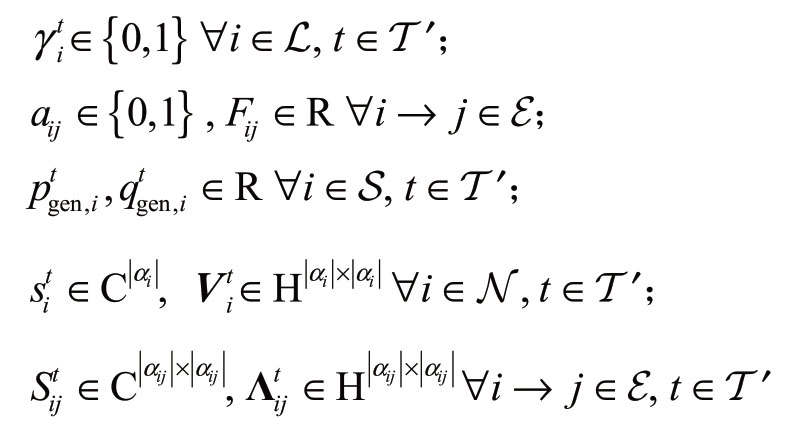
约束条件:
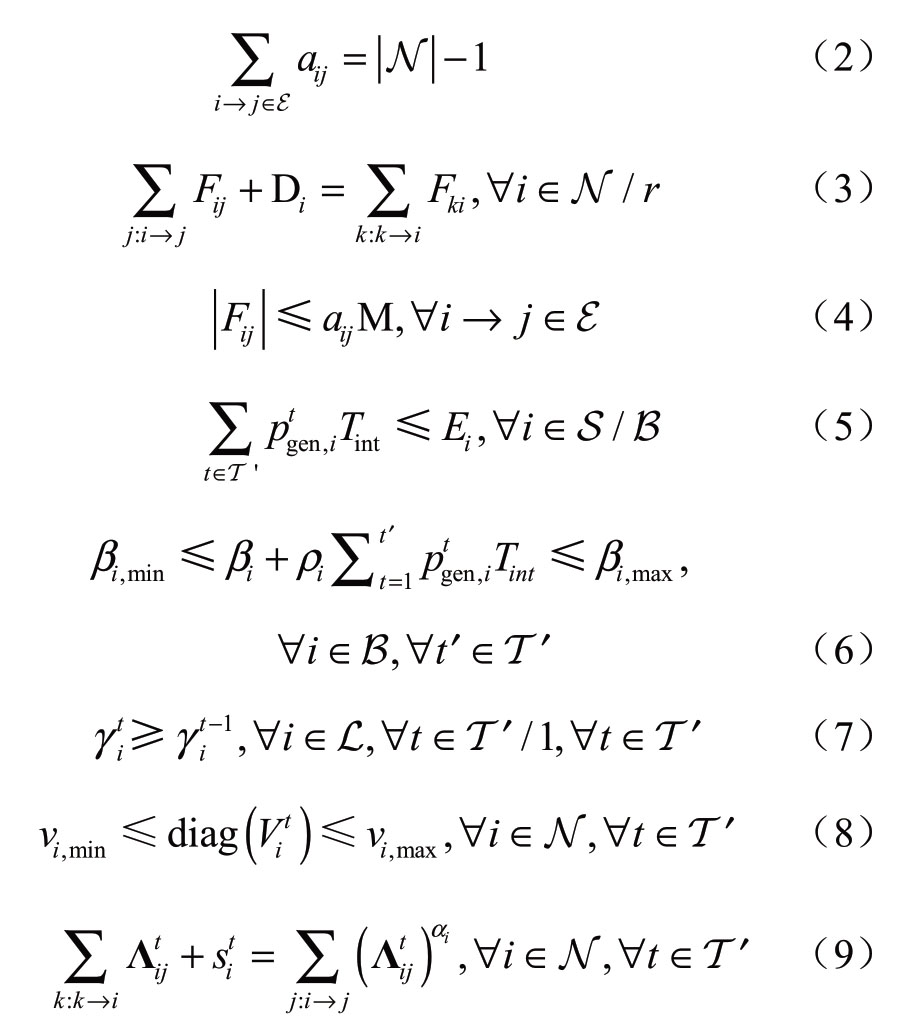
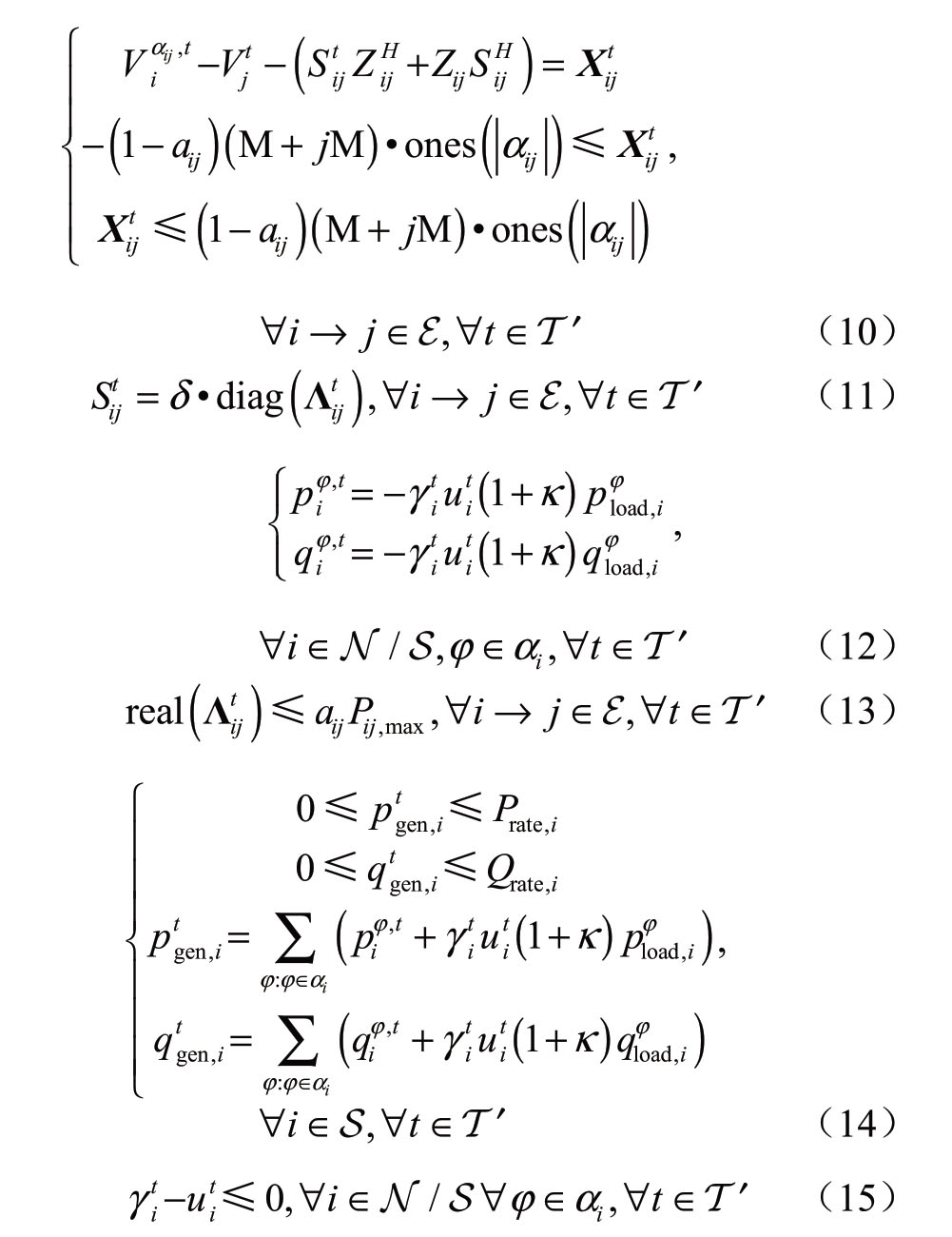
式中:大写加粗的符号均表示矩阵或矩阵变量,小写加粗的符号表示向量或向量变量; 和
和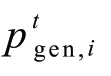 均为该时段中恢复策略给出的值,为已知量分别表示i号节点的负荷在时段t的恢复状态和发电机的有功功率值;所有带t上标的字符表示相应含义在t时段的值;Fij为连续变量,代表线路i→j流过的虚拟潮流大小;Di、r和M均为已知常量,分别表示非根节点虚拟需求(一般可设为1)、根节点编号和数值很大的正实数(一般可设为节点数目)。Ei表示电源i当前剩余的发电资源(包括柴油或天然气等)的能量(kWh),该值在每时段确定策略前需要根据上一时段能量消耗情况进行更新;B表示储能设备的集合,本文中主要考虑电化学储能,且有B∈S ;βi、βi,min和βi,max分别表示电池类电源i荷电状态的当前值、最小值和最大值,该常量的值在0到1之间;ρi为转换系数,将能量转换为该设备的荷电状态。vi,min和vi,max为节点i各相电压幅值最小值/最大值的平方构成的常数向量。函数diag(●)代表取括号内向量各个元素为对角线元素形成对角矩阵。引入辅助变量
均为该时段中恢复策略给出的值,为已知量分别表示i号节点的负荷在时段t的恢复状态和发电机的有功功率值;所有带t上标的字符表示相应含义在t时段的值;Fij为连续变量,代表线路i→j流过的虚拟潮流大小;Di、r和M均为已知常量,分别表示非根节点虚拟需求(一般可设为1)、根节点编号和数值很大的正实数(一般可设为节点数目)。Ei表示电源i当前剩余的发电资源(包括柴油或天然气等)的能量(kWh),该值在每时段确定策略前需要根据上一时段能量消耗情况进行更新;B表示储能设备的集合,本文中主要考虑电化学储能,且有B∈S ;βi、βi,min和βi,max分别表示电池类电源i荷电状态的当前值、最小值和最大值,该常量的值在0到1之间;ρi为转换系数,将能量转换为该设备的荷电状态。vi,min和vi,max为节点i各相电压幅值最小值/最大值的平方构成的常数向量。函数diag(●)代表取括号内向量各个元素为对角线元素形成对角矩阵。引入辅助变量![]()
![]() 以说明矩阵变量的含义:矩阵变量
以说明矩阵变量的含义:矩阵变量![]() Λij为向量变量,取自变量矩阵Sij中的对角线元素;向量变量
Λij为向量变量,取自变量矩阵Sij中的对角线元素;向量变量![]() 为注入功率向量,其中
为注入功率向量,其中![]() AH代表矩阵A的共轭转置矩阵;
AH代表矩阵A的共轭转置矩阵;![]() 矩阵变量Xij为中间变量。ones(m)代表所有元素均为1的行数列数均为m的方阵;δ为常数矩阵,且
矩阵变量Xij为中间变量。ones(m)代表所有元素均为1的行数列数均为m的方阵;δ为常数矩阵,且
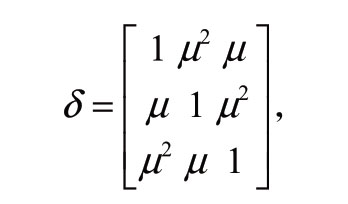
其中µ=e-πj2/3;κ为网损因子,为网络正常运行时有功网损占有功负荷的比率;Pij,max为已知实数向量,意为线路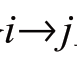 上流过有功功率的限值;uti为已知常量,表示负荷i在时段t是否在线,即是否接入配电网,在线则为1,不在线为0,该值可以根据对应负荷自备应急电源的后备时间确定。
上流过有功功率的限值;uti为已知常量,表示负荷i在时段t是否在线,即是否接入配电网,在线则为1,不在线为0,该值可以根据对应负荷自备应急电源的后备时间确定。
约束(2)-(4)为目标孤岛恢复后网络的辐射状约束,由于孤岛只有1个,因此根节点只有1个。其中(2)表示所有闭合线路的个数等于所有节点数减去1,此约束为生成的图为树的必要条件,而约束(3)-(4)为单商品流约束,确保图的连通性:约束(3)表示对于除根节点外的所有节点来说,满足流入的虚拟流等于流出的虚拟流;约束(4)表示用“大M法”区分线路闭合和断开两种情况:若线路闭合则对流过线路的虚拟流大小不作约束,反之则为0。约束(5)和(6)表示能量约束,其中约束(5)表示非储能类电源i在恢复中消耗的总能量不能超过其初始能量值;约束(6)表示在任意时段中,储能类电源i的荷电状态均要保持在最小值和最大值之间,以确保电池类设备的安全运行和使用寿命。约束(7)表示为了防止负荷状态在恢复过程中频繁变化,仅允许负荷状态变化1次,即从不恢复状态变为恢复状态。约束(8)为节点电压幅值约束。约束(9)意为对于任意节点i,从网络其他所有节点流入节点i的功率与从外界注入节点i的功率之和等于从节点i流向网络其他节点的功率之和。约束(10)表示线路两端电压幅值的关系。约束(11)表示Sij与Λij的关系。约束(12)为负荷节点注入功率约束。约束(13)为线路流过的有功功率约束,由于该模型中并无电流变量,因此使用有功功率约束简要代替电流约束。约束(14)为电源节点注入功率约束,约束(15)为负荷在线状态与负荷恢复状态的关系。
以上,建立了多时段恢复问题的混合整数线性规划模型MPCLR-milp。该模型可以通过成熟的商业优化求解器进行求解。
3 各时段优化运行策略
对于任意时段,得到滚动修正后的恢复计划后,用VER的最小功率预测值,修正该时段的运行策略参数。优化运行策略的目标函数为最小化系统的有功网损以及最小化发电机功率调节量。考虑的约束条件包括潮流约束、电压约束、电流约束等。某时段运行优化OP-sdp模型如下:
其中变量:

约束条件:(8)
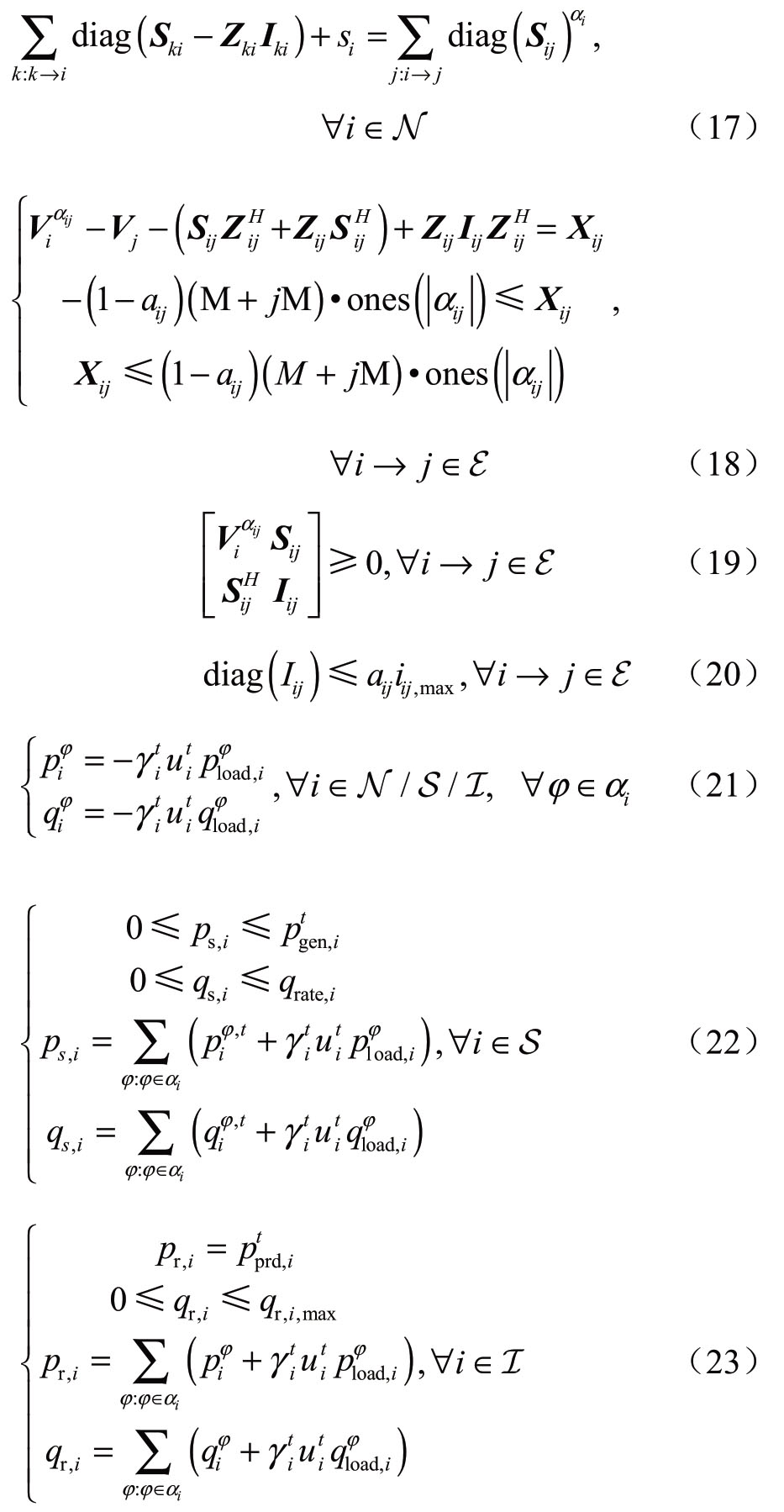
其中,引入向量变量![]() 矩阵变量
矩阵变量![]() iij,max为线路(i,j)幅值最大值的平方构成的常数向量。集合I为所有可再生能源构成的集合;ps,i和qs,i表示运行策略中各台可控电源的有功无功功率,pr,i和qr,i表示运行策略中可再生能源的有功功率和无功功率;pprd,i表示可再生能源i在t时段的有功功率预测最小值,为已知量,qr, ,maxi 为间歇性能源i的无功功率最大值,亦为已知量。
iij,max为线路(i,j)幅值最大值的平方构成的常数向量。集合I为所有可再生能源构成的集合;ps,i和qs,i表示运行策略中各台可控电源的有功无功功率,pr,i和qr,i表示运行策略中可再生能源的有功功率和无功功率;pprd,i表示可再生能源i在t时段的有功功率预测最小值,为已知量,qr, ,maxi 为间歇性能源i的无功功率最大值,亦为已知量。
约束(21)表示负荷节点注入功率约束。约束(22)为可控电源功率输出限制约束,所有可控电源有功功率上限为恢复策略给出的有功功率值。约束(23)为可再生能源功率输出限制约束,为降低出力不确定性对运行的影响,以其最小出力预测值作为其出力值,做该时段的运行计划。
该模型为半定规划模型,可以利用成熟商业优化求解器有效求解。若求出的解满足半定矩阵的秩为1,则求出的解是全局最优解。
4 算例及方法验证
4.1 算例描述
本文利用改进的IEEE123节点算例进行验证,其拓扑结构如图2所示,基本参数可见文献[4]。其中,风电和光伏的额定功率均为50 kW,且随时间出力变化归一化曲线如图3所示[21]。假设极端事件后变电站均失电,配电网内发生多点故障,三个微电网转入孤岛运行状态,微电网以外的负荷全部失电,事件后状态如图2所示,所有电源皆可用于恢复。预计配电网停电时间为6 h,为早上10:00至下午4:00。此时协同网内的可控分布式电源、自备应急电源、VRE-DG共同实现应急供电恢复。
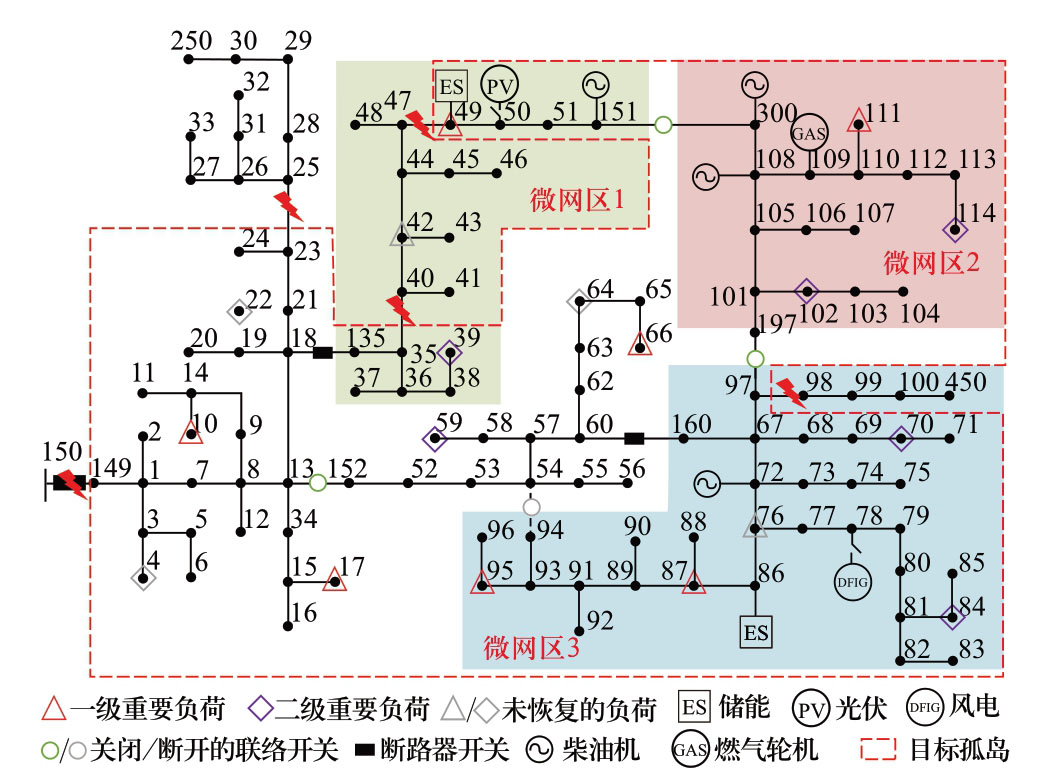
图2 改进的IEEE123节点算例拓扑图
Fig.2 Modified IEEE 123-node test system
假设极端事件后,节点150所连变电站失电,3个微电网均转为孤岛运行状态。配电网内出现多点故障,即线路23-25、35-40、47-49、97-98和149-150故障断开。
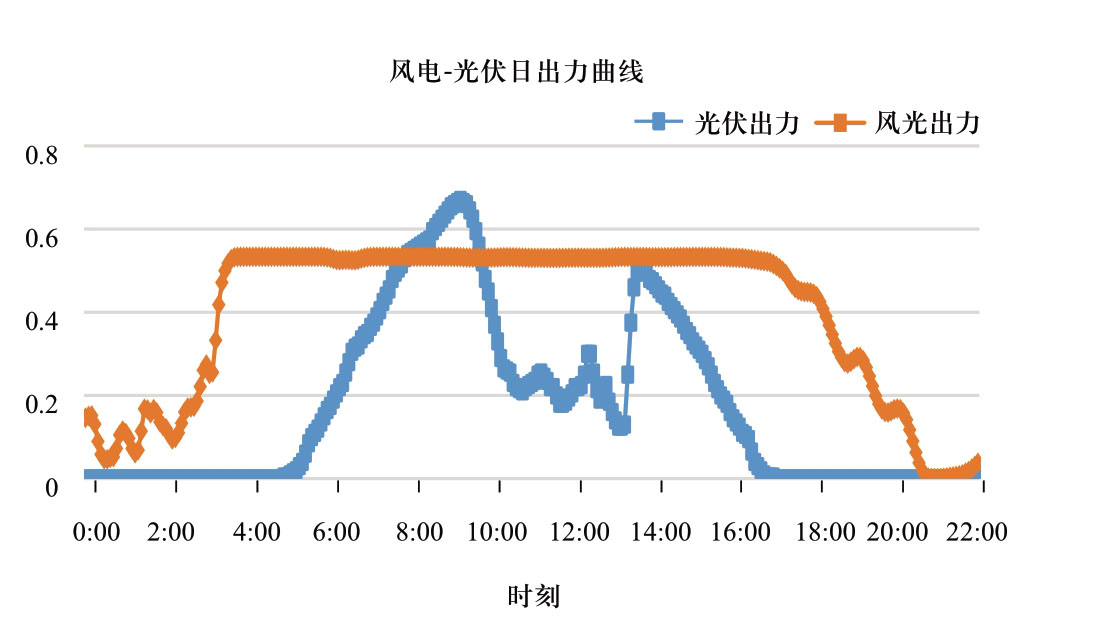
图3 光伏-风电日出力曲线
Fig.3 Power curves of photovoltaics and wind turbines
4.2 第1时段的恢复计划
在该场景下,恢复后可形成1个目标孤岛。将预计停电时段分为12时段,每个时段为30 min。用 OP-sdp求解应急供电恢复计划模型MPCLR-milp,网损因子取0.3%。MPCLR-milp求解时间为1491.16 s,得到恢复策略如图4所示。
前2时段,即10:00-11:00期间,一级和二级重要负荷均通过自备应急电源供电,可全部恢复;第2时段过后一级重要负荷继续通过自备应急电源供电,二级负荷并入孤岛电网,其中6个二级负荷恢复供电。第4时段过后,一级重要负荷自备应急电源能量耗尽,7个一级负荷均并入孤岛电网运行。
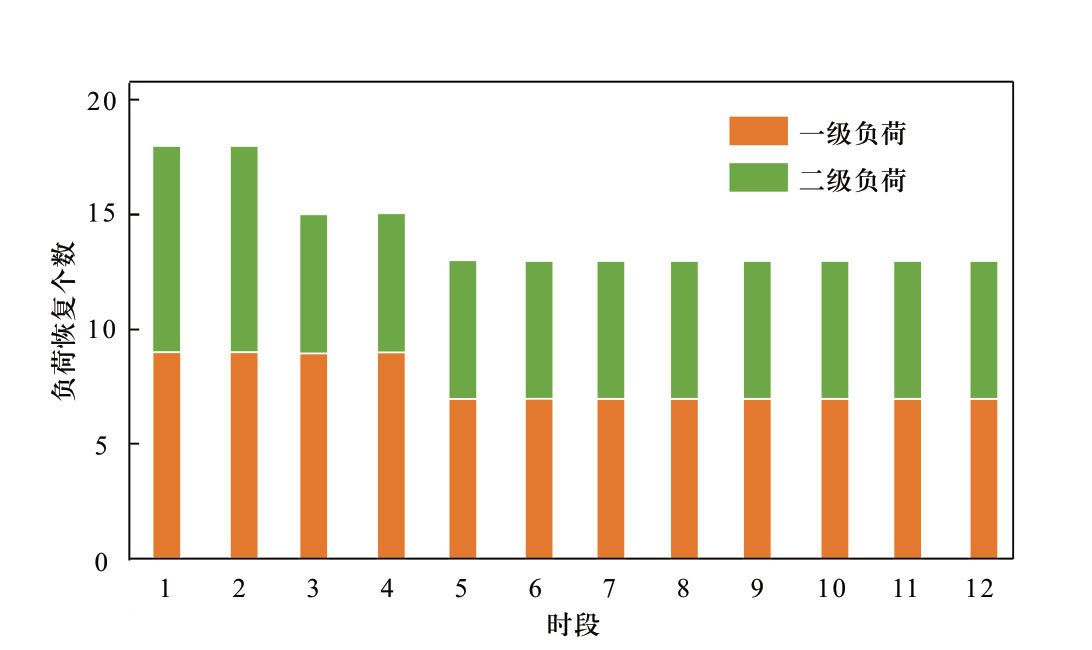
图4 改进的IEEE123节点系统第一时段的恢复计划
Fig.4 Multi-period restoration plan in the 1st period for modified IEEE 123-node system
在第一时段,即上午10:00-10:30,恢复策略为不恢复网内负荷,7台可控电源出力情况见表1,即两个储能处于充电状态。通过求解OP-sdp,0.22 s得到运行策略,预测50号节点光伏在10:00-10:30最小出力为29.75 kW,78号节点风电为26.56 kW。根据光伏和风电出力预测值得到优化后的7个可控电源出力如表1所示。引入“δ′”来衡量OP-sdp模型的解是否是精确,即相关矩阵变量的值的秩是否接近1。为了衡量某个矩阵的秩是否接近于1,则求得该矩阵绝对值最大的两个特征根λ1,![]() 两个特征根的绝对值之比为
两个特征根的绝对值之比为![]() 越小,表示该矩阵的秩越接近于1。δ′ 是所有矩阵变量特征根绝对值之比的最大值,即:
越小,表示该矩阵的秩越接近于1。δ′ 是所有矩阵变量特征根绝对值之比的最大值,即:

本算例中δ′= ×2.22 10-5,即OP-sdp模型的求解是数值精确的,即满足松弛掉的秩1约束。
表1 第一时段恢复计划和运行策略中各电源功率输出情况
Table1 Power outputs of all sources in the multi-period restoration plan and operation plan in the 1st period

从表1中可以看出,在第1时段,恢复计划中未考虑VRE-DG,为2台储能充电,而在实时运行控制中考虑可再生能源的参与,可节省可控电源的能量28.16 kWh。
4.3 滚动修正的恢复情况
根据图3所示的风电和光伏出力曲线,滚动计算得到各时段负荷恢复情况如图5所示。其中,相比于第1时段得到的多时段恢复计划,虽然在第3时段少恢复了2个二级负荷,但在第10-11时段增加恢复了一级负荷76。可以看出,考虑VRE-DG的应急供电恢复策略,相比于不利用VRE-DG的多时段恢复策略,负荷加权供电时间为5220 h,增加240 h,恢复能量增加334.69 kWh。可见,本文提出的利用VRE-DG辅助恢复的应急供电恢复策略能够更大限度地利用发电资源,保证重要负荷供电时间,同时扩大恢复供电范围。
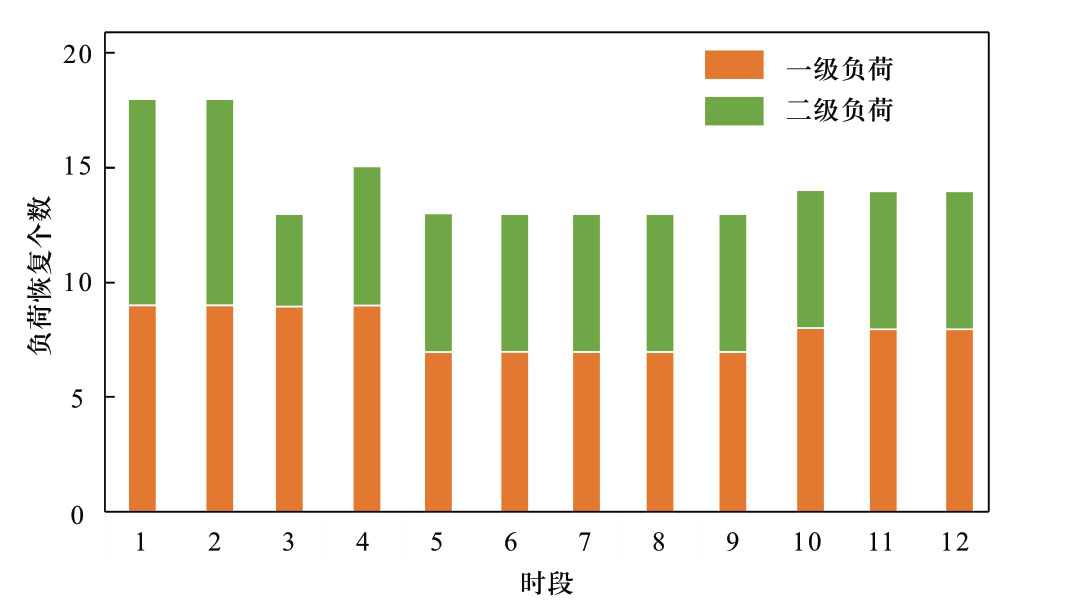
图5 改进的IEEE123节点系统最终的负荷恢复情况
Fig.5 Final power supply restoration result for the modified IEEE 123-node system
5 结论
本文考虑VRE-DG对应急恢复的能量支撑,提出了计及VRE-DG的配电网应急供电恢复策略,通过滚动求解多源协同多时段恢复模型MPCLR-milp和优化运行模型OP-sdp确定各时段的恢复策略和运行策略。与不使用VRE-DG的应急供电恢复策略相比,本文方法针对123节点配电网,应急恢复策略中负荷加权供电时间增加240 h,恢复能量增加334.69 kWh,表明本文提出方法能够保证重要负荷供电时间,同时扩大恢复供电范围,从而提升恢复效果。
参考文献
[1]刘飞,汤亮亮,邓鹤鸣,等.计及分布式电源的城市重要用户应急电源优化配置[J].全球能源互联网,2018,1(5):581-588.
LIU Fei,TANG Liangliang,DENG Heming,et al.Optimal Allocation of Emergency Power Supply of Urban Important Loads Considering Distributed Generation[J].Journal of Global Energy Interconnection,2018,1(5):581-588(in Chinese).
[2]CHEN C,WANG J H,QIU F,et al.Resilient distribution system by microgrids formation after natural disasters[J].IEEE Transactions on Smart Grid,2016,7(2):958-966.
[3]KHEDERZADEH M,ZANDI S M.Enhancement of distribution system restoration capability in single/multiple faults by using microgrids as a resiliency resource[J].IEEE Systems Journal,2019,13(2):1796-1803.
[4]WANG Y,XU Y,HE J H,et al.Coordinating multiple sources for service restoration to enhance resilience of distribution systems[J].IEEE Transactions on Smart Grid,2019,10(5):5781-5793.
[5]文娟,谭阳红,何怡刚,等.含分布式电源的复杂配电网多阶段故障恢复方法[J].电工技术学报,2018,33(14):3332-3341.
WEN Juan,TAN Yanghong,HE Yigang,et al.A multistage service restoration method for complex distribution networks with distributed generators[J].Transactions of China Electrotechnical Society,2018,33(14):3332-3341(in Chinese).
[6]XU Y,LIU C C,SCHNEIDER K P,et al.Microgrids for service restoration to critical load in a resilient distribution system[J].IEEE Transactions on Smart Grid,2018,9(1):426-437.
[7]XU Y,LIU C C,WANG Z W,et al.DGs for service restoration to critical loads in a secondary network[J].IEEE Transactions on Smart Grid,2019,10(1):435-447.
[8]刘志谱,李欣然,刘小龙,等.考虑负荷重要性与源-荷互补性的负荷恢复策略[J].全球能源互联网,2019,2(5):449-456.
LIU Zhipu,LI Xinran,LIU Xiaolong,et al.Load recovery strategy considering importance and source-load complementarity[J].Journal of Global Energy Interconnection,2019,2(5):449-456(in Chinese).
[9]GAO H X,CHEN Y,XU Y,et al.Resilience-oriented critical load restoration using microgrids in distribution systems[J].IEEE Transactions on Smart Grid,2016,7(6):2837-2848.
[10]CHEN B,CHEN C,WANG J H,et al.Sequential service restoration for unbalanced distribution systems and microgrids[J].IEEE Transactions on Power Systems,2018,33(2):1507-1520.
[11]WANG Z Y,WANG J H,CHEN C.A three-phase microgrid restoration model considering unbalanced operation of distributed generation[J].IEEE Transactions on Smart Grid,2018,9(4):3594-3604.
[12]WANG Z Y,CHEN B K,WANG J H,et al.Networked microgrids for self-healing power systems[J].IEEE Transactions on Smart Grid,2016,7(1):310-319.
[13]CHEN B,CHEN C,WANG J H,et al.Multi-time step service restoration for advanced distribution systems and microgrids[J].IEEE Transactions on Smart Grid,2018,9(6):6793-6805.
[14]WANG Z W,SHEN C,XU Y,et al.Risk-limiting load restoration for resilience enhancement with intermittent energy resources[J].IEEE Transactions on Smart Grid,2019,10(3):2507-2522.
[15]刘伟佳,孙磊,林振智,等.含间歇电源、储能和电动汽车的配电孤岛短时恢复供电策略[J].电力系统自动化,2015,39(16):49-58.
LIU Weijia,SUN Lei,LIN Zhenzhi,et al.Short-period restoration strategy in isolated electrical Islands with intermittent energy sources,energy storage systems and electric vehicles[J].Automation of Electric Power Systems,2015,39(16):49-58(in Chinese).
[16]WANG Z Y,WANG J H.Self-healing resilient distribution systems based on sectionalization into microgrids[J].IEEE Transactions on Power Systems,2015,30(6):3139-3149.
[17]YUAN W,WANG J H,QIU F,et al.Robust optimizationbased resilient distribution network planning against natural disasters[J].IEEE Transactions on Smart Grid,2016,7(6):2817-2826.
[18]XU J J,WU Z J,YU X H,et al.A dynamic robust restoration framework for unbalanced power distribution networks[J].IEEE Transactions on Industrial Informatics,2020,16(10):6301-6312.
[19]FARZIN H,FOTUHI-FIRUZABAD M,MOEINI-AGHTAIE M.Enhancing power system resilience through hierarchical outage management in multi-microgrids[J].IEEE Transactions on Smart Grid,2016,7(6):2869-2879.
[20]许寅,王颖,和敬涵,等.多源协同的配电网多时段负荷恢复优化决策方法[J].电力系统自动化,2020,44(2):123-133.
XU Yin,WANG Ying,HE Jinghan,et al.Optimal decisionmaking method for multi-period load restoration in distribution network with coordination of multiple sources[J].Automation of Electric Power Systems,2020,44(2):123-133(in Chinese).
[21]Zhang Y.Solar power data for integration studies[EB/OL].[2018-12-05].https://www.nrel.gov/grid/solar-power-data.html.
收稿日期:2020-07-13;修回日期:2020-10-09。
Service Restoration Strategy for Distribution Systems Considering Renewable-energy-based Distributed Generators
LIU Jiayu1,ZHANG Qiqi1,WANG Ying2*,XU Yin2
(1.State Grid Shanghai Electrical Power Company Research Institute,Shanghai 200437,China;2.School of Electrical Engineering,Beijing Jiaotong University,Beijing 100044,China)
Abstract: In distribution systems,the energy stored in local controllable distributed generations is usually limited.In contrast,considerable energy can be obtained from variable renewable energy-distributed generation (VRE-DG) resources,such as photovoltaic cells and wind power,under suitable weather conditions.Thus,VRE-DG can be used to restore the power supply from distribution systems in extreme poweroutage scenarios.However,the resulting electrical island,without support from bulk grids,is susceptible to disturbances,and the VRE-DG output is uncertain.This may result in powersupply imbalance or even restoration failure.To address these concerns,this paper presents an emergency power-supplyrestoration strategy.By solving the multi-period restoration and optimal operation models at the beginning of each period,the proposed method is used to determine the restoration strategy and optimal operating state of the period.The results of case studies reveal that the proposed method minimizes the risk of restoration failure due to VRE-DG uncertainty,thereby facilitating the provision of necessary support from VRE-DG for power-supply restoration.
Keywords: distribution-system restoration;resilience;renewable energy;optimal decision-making
Science and Technology Foundation of SGCC (B30940190000).
作者简介:

刘家妤
刘家妤(1986),女,硕士,高级工程师,主要研究方向为韧性电网、电气设备状态监测与故障诊断、现场特殊试验、超导电缆技术研究与应用等,E-mail:liujiayu04@gmail.com。
张琪祁(1985),女,硕士,主要研究方向为韧性电网、电力系统仿真和控制等,E-mail:sh_kjjl@163.com。
王颖(1992),女,博士,讲师,主要研究方向为韧性、配电网恢复、电力交通融合等。通信作者,E-mail:yingwang1992@bjtu.edu.cn。
许寅(1986),男,博士,教授,博士生导师,主要研究方向为韧性电网、电力系统高性能计算、电力交通融合等,E-mail:xuyin@bjtu.edu.cn。
(责任编辑 张鹏)
