0 引言
近年来,由于电网和天然气网耦合所构成的电-气综合能源系统(integrated electric power and natural gas system,IEGS)具有提高能源利用效率、提高可再生能源消纳能力以及降低用户的用能成本等优势逐渐受到了业界的关注和重视[1-3]。配电终端中,构建园区能源互联网等多能耦合程度的加深使得传统配电网的优化需注重多能耦合系统之间的相互影响,并在优化模型中加以考虑。配电网重构是配电网实现优化运行的一种有效措施,它只需对配电网的开关组合进行调整,无需增加投资即可达到均衡负荷、提高电压质量和降低网损等目的[4-5]。因其具有快速操作、均衡负载的优势,故除了促进配电网自身优化水平提升的效果外,在耦合的IEGS中也有望提升两个系统互补互济的效能。
各国对配电网网络重构有较多研究,文献[6-7]研究了配电网重构对提高消纳可再生能源能力的积极作用;文献[8-9]分别利用改进布谷鸟算法和最佳等距分段线性化逼近方法对计及三相不平衡的有源配电网进行网络重构,改善了配电网的三相不平衡度;文献[10]综合考虑网损、开关动作次数、电压质量以及馈线负载均衡度构建了含柔性多状态开关的配电网多目标重构模型。以上文献重点在电网领域对配电网的作用进行研究,对于IEGS中配电网的网络优化重构研究仍在起步阶段,文献[11]融合配电网重构研究了多能耦合的最优混合潮流算法;文献[12]从综合规划的角度出发,研究了考虑配电网重构的城市多能源配电/气/热网扩展规划。但IEGS中配网重构还未考虑系统中不确定因素对重构方案适应性造成的影响。
随着IEGS中风光等可再生能源广泛接入,配电网重构面临源荷不确定性增强的问题。文献[13]利用区间数描述分布式电源和负荷预测的不确定性,构建了以网损区间值最低为目标的重构模型;文献[14]采用分布式鲁棒优化方法处理可再生能源不确定性,并构建了主动配电网重构模型;文献[15]利用区间数方法提出了一种考虑电动汽车充电和分布式电源出力不确定性的主动配电网优化重构模型。以上文献考虑不确定因素的存在,采用随机规划方法,利用鲁棒、区间等较为保守的风险描述手段保证状态变量在任一抽样场景中满足,结果虽严格保证了安全性,但往往趋于保守,使得经济性降低。
为充分发挥多能系统耦合的优势,基于配电网重构的快速有效手段,提升IEGS的综合运行优化水平,降低源荷不确定带来的风险,本文构建了考虑配电网重构的IEGS优化运行模型,模型中引入经济学领域广泛应用的条件风险价值(conditional value at risk,CVaR)理论,建立考虑系统运行期望成本和风险成本的目标函数,相比传统的机会约束规划具有可量化风险、数学特性好(如凸性)等优势[16-17]。同时考虑IEGS多能源耦合网络约束,将配电网重构映射到IEGS运行优化模型中,潮流模型中引入重构开关控制变量相关线性化处理约束,含构造松弛节点电压变量对电压约束进行修正,以及利用增加虚拟单位负荷的功率平衡约束保证配电网的辐射状,建立凸化潮流模型。算例仿真对比分析了考虑配网重构与否、计及CVaR与否以及置信水平对IEGS优化调度的影响。
1 IEGS的组成与建模
IEGS以配电网、配气网为传输载体,以能源中心为电-气耦合单位,能源中心集成了多种能源的转换、储存设备,实现多能耦合交互与供给,典型结构如图1所示。本文将系统划分成配电子系统模型、配气子系统模型和能源中心子系统模型三大部分进行建模。
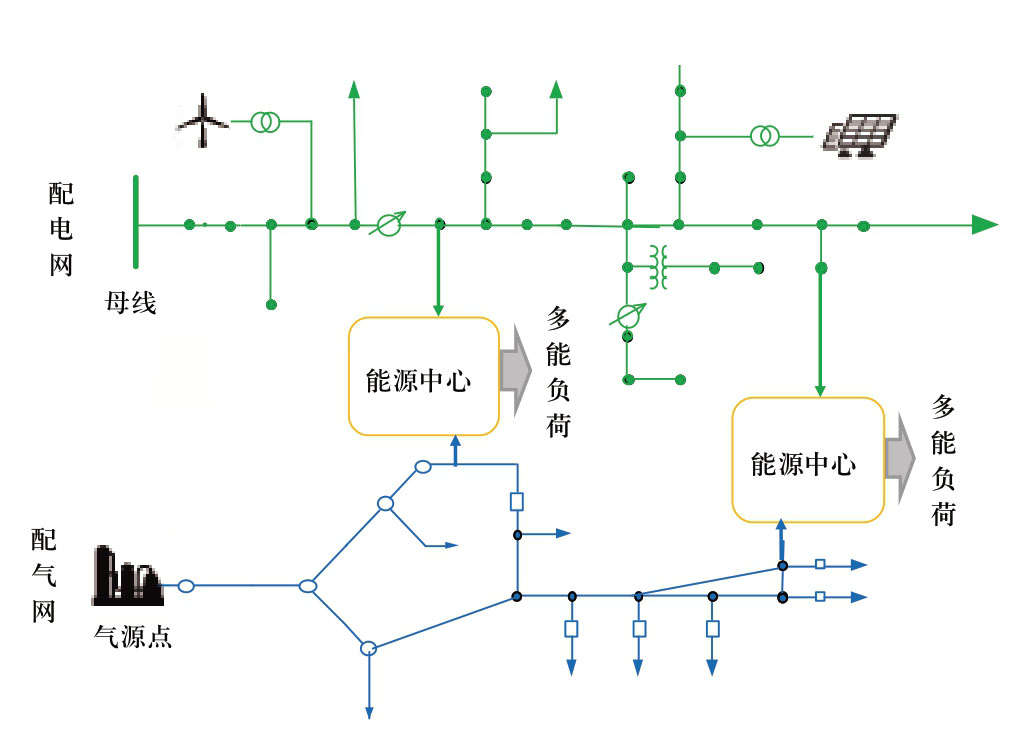
图1 IEGS典型结构示意图
Fig.1 Schematic diagram of IEGS typical structure
1.1 配电子系统模型
本文采用支路潮流模型描述配电子系统中支路传输功率与节点电压-相角之间的关系[18-19],方程表达为
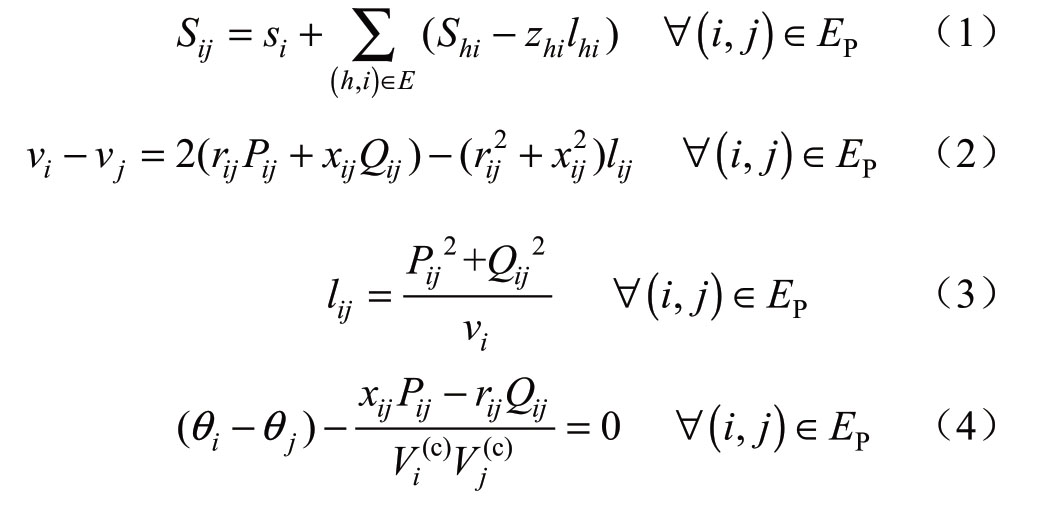
式中:下标i、j、h均为配电子系统节点号,复合下标ij为以节点i为首端、节点j为末端构成的配电线路,下标hi同理;EP表示所有配电线路的集合;v、θ分别为节点电压幅值的平方、节点电压相角,l为流经配电线路电流幅值的平方;z=r+jx表示线路的阻抗值;S=P+jQ表示从流经线路的复功率,P和Q分别为有功功率和无功功率;s为节点注入的净复功率;V(c)表示考虑节点电压幅值为常数的变量。
进一步地,基于文献[18-19],利用二阶锥松弛将支路潮流模型的非凸二次项约束,即式(3)转化为凸的二阶锥约束,以提高潮流约束在优化问题中的求解效率,则有:
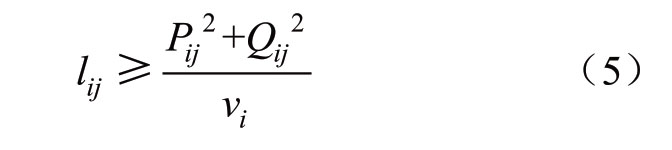
由式(1)、(2)、(4)、(5)构成的可行域为凸锥体,利用如Mosek的求解器能高效对其进行求解。文献[19]证明了此二阶锥松弛的严格收敛条件。
1.2 配气子系统模型
与配电子系统类似,配气子系统以节点气压和流经支路气体流量为状态量,基于Weymouth方程构建了状态量之间的关系[20]:
式中:下标m、n为配气子系统节点号,复合下标mn为以节点m为首端、节点n为末端构成的输气管道;EG表示所有输气管道的集合;ω为流经管道的流量;π节点的气压值;sgn为符号函数;K为管道特性系数。
对于任一节点,节点流量平衡关系表示为
式中:W为节点净注入流量。
1.3 能源中心子系统模型
能源中心子系统主要从上级配电、配气系统中的获得功率/流量,并基于能源中心内能源转换、存储等设备实现多能耦合互补,满足多能负荷(电、冷、热、气等)需求。能源中心子系统可描述为能量输入-输出的二端口网络,并基于能量枢纽(energy hub)建模方法进行建模[21-22],抽象数学模型为
式中:PEH、LEH分别为能源中心的能源输入功率向量及能源输出(负荷)向量。函数f(·)为表征各种形式能源转换、传输的关系式。本文的研究对象为电气综合能源系统,能源中心的耦合主要指电与气的耦合设备元件,如燃气轮机及由燃气轮机等设备组成的冷热电三联产设备。
2 计及CVaR的IEGS配电网优化重构模型
IEGS中的配电网优化重构,以配网开关动作为决策量,综合考虑多能耦合约束并提升IEGS优化潜力。为评估源-荷不确定性带来运行风险,本文采用CVaR理论对风险进行评估量化。
2.1 CVaR理论
CVaR是基于VaR提出的一种改进风险分析方法,克服了VaR方法不能描述在不利情况发生时对损失程度的缺陷及其在次可加性上的不足[23-24]。对任一决策x,假设由系统不确定因素ξ扰动造成的损失成本为H(x,ξ),则CVaR的含义为H(x,ξ)超过阈值VaR时所造成的风险水平的平均值。VaR的值由置信水平β决定,计算如式(9),而CVaR表达式如式(10)。

式中:P(ξ)为ξ的概率密度函数。
由式(10)可知,CVaR需事先求解VaR,给计算带来不便。基于文献[23],可引入辅助变量z,构造关于z的最小化优化问题对CVaR进行求解。并且,用各抽样场景下的离散点来代替式(10)中的积分项,则式(10)等价于:
式中:ξs为ξ的第s(s=1,2,…,S)个样本,为样本s对应的概率。
2.2 目标函数
IEGS优化重构模型的目标函数为运行成本最小。运行成本除了IEGS与上级电网、天然气网交互能量费用,还包括为处理源-荷不确定性,维持系统稳定所造成的运行风险成本。
结合式(11)对系统不确定因素进行量化,将IEGS中源-荷不确定离散为多个场景后,IEGS中任一场景的运行成本Cs表示为
式中:Cop,s、Cr,s分别为系统在第s个场景下的运行成本和风险成本,具体表达式阐述如下(为简洁表述,以下对两成本描述略去下标s)。
1)系统运行成本Cop。
Cop包含配电、配气系统向上层能源系统购置成本,即
式中:ρe和ρg分别是购电价和购气价;Pe和Wg分别为上级电网供电量和供气量。
2)系统风险成本Cr。
系统风险成本由切负荷和弃能成本构成,考虑能源中心含电、热多能负荷,则含配电、配气系统在内切负荷包括电负荷、气负荷和热负荷,而弃能成本则包括风机弃风成本和光伏弃光成本,即

式中:![]() 分别为切电负荷、气负荷和热负荷的风险惩罚成本系数;
分别为切电负荷、气负荷和热负荷的风险惩罚成本系数;![]() 分别是切电负荷、切气负荷和切热负荷总量;cwind和cPV分别是弃风、弃光的风险惩罚成本系数;Dwind和DPV分别是弃风和弃光的总量。
分别是切电负荷、切气负荷和切热负荷总量;cwind和cPV分别是弃风、弃光的风险惩罚成本系数;Dwind和DPV分别是弃风和弃光的总量。
基于式(12)—(14)的场景成本构建,结合式(11)的CVaR不确定风险量化理论,考虑场景成本的成本期望和风险量化,则IEGS中配电网优化重构模型的目标函数FC可表示为
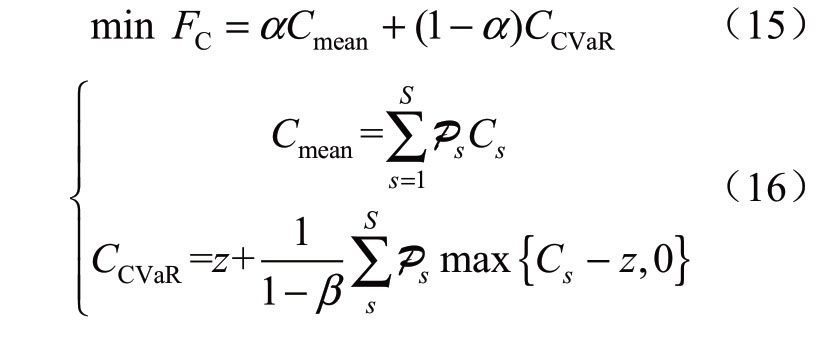
式中:Cmean为重构后IEGS系统运行的期望成本,体现为均值成本;CCVaR为重构后IEGS风险评估成本;α∈[0,1]为权重系数。
2.3 IEGS配电网重构控制量约束及其线性化
1)支路开断潮流约束。
开关的闭合是配电网重构的主要控制变量,其会直接影响到电力网络的潮流分布,需对支路潮流的电压约束,即式(2)进行修正,结合图2描述如下。
图2 线路开断示意图
Fig.2 Schematic diagram of line switch
如图2所示,当开关闭合,vi和vj需要满足电压约束,支路流经功率和电流均要满足上下限约束。当开关断开后,vi和vj不用满足任何约束,且两节点间流过的功率和电流均为0。
因此,引入松弛节点电压变量vij,离散变量δij,对约束(2)进行改进,构造线性化约束为
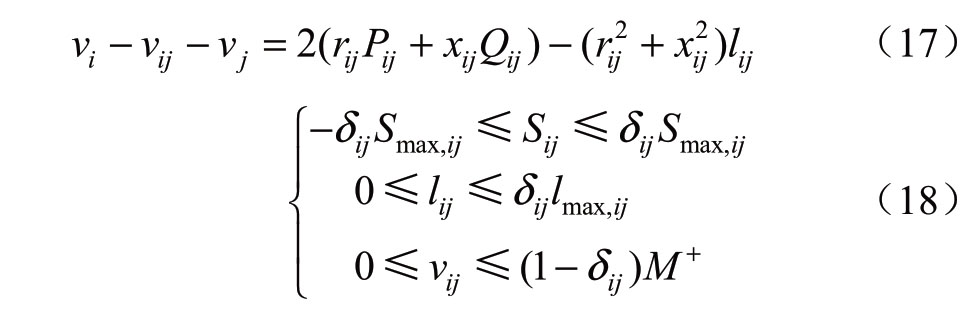
式中:Smax,ij、lmax,ij分别为支路ij的最大传输容量和最大电流的平方,M+为任意较大数。
由式(17)—(18)知,当δij=1,支路开关闭合,此时vij=0,式(17)退化为式(2),且过线路ij的电流lij和功率Sij满足相应支路电流和支路容量约束。而当δij=0时,支路开关断开,lij和Sij均为0,与支路断开情况相符。
2)配电网辐射状约束。
基于文献[25],对于一个含I个节点的配电系统,若配电系统中不含传输节点(传输节点指节点净注入功率为0),结合前述的潮流方程约束,配电系统为辐射状的充要条件为
式中:η为配电系统供电电源数,对于一个配电馈线,由于不考虑内含分布式能源使其孤岛运行,则电源数为1,即配电馈线终端与上级交互点视为电源点。
为消除配电系统中不含传输节点这一假设条件,本文引入虚拟单位负荷的概念,即利用同一个待优化的拓扑网络,令除电源点外各个节点均有单位负荷s'i,构建单位负荷响应下的无损潮流线性表达式为
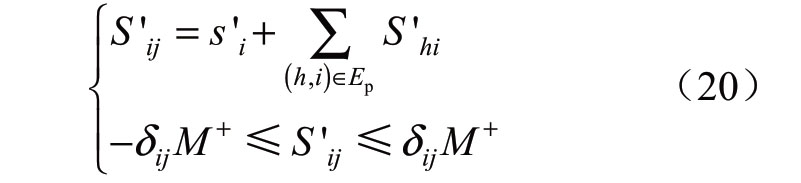
式中:S'为单位负荷响应下各支路的传输功率。可见,增加虚拟单位负荷,并构造虚拟负荷响应下的潮流约束表达式,满足了配电系统中不含传输节点这一假设条件,进而使增加的约束式(19)—(20)满足配电网辐射状约束。
2.4 IEGS状态量约束
1)配电子系统状态量约束。
1.1节描述了由节点-支路构成的配电系统潮流关系,配电子系统运行除需满足其潮流约束,还需满足节点电压、支路潮流不越限约束。其中,潮流关系及支路潮流约束为式(1)、(4)—(5)、(17)—(18),节点电压约束见式(21)。
式中:vimin和vimax分别为节点i电压最小值和最大值的平方。
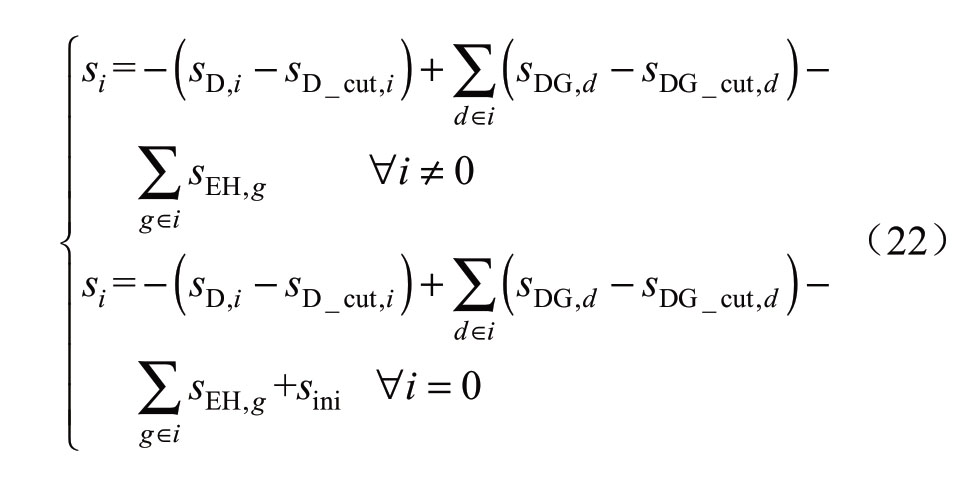
此外,由于目标函数中增加了切负荷和弃能考虑,并且由于能源中心的耦合,故式(1)中关于节点净注入的复功率s可表示为式中:i=0指配电子系统线路首端(即与上级电网交互节点);sini为交互功率,为待求量;下标变量d、g分别为分布式能源(含风电、光伏等)、能源中心子系统的计数变量;sD和sDG分别为负荷和分布式能源预测出力的复功率,为常量;sEH为输入能源中心子系统的电功率需求;sD_cut和sDG_cut为切负荷和弃能功率变量,两者需满足可切、可弃能量最大值约束。
2)配气子系统状态量约束。
与配电子系统类似,配气子系统运行除需满足式(6)—(7)的气体流量约束外,流经管道流量及节点气压需满足限值约束,即
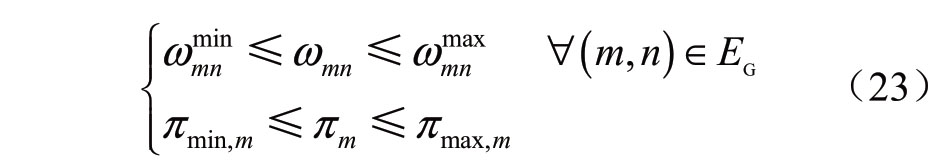
式中: 和
和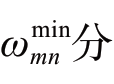 别为管道mn允许通过的天然气流量的最大值和最小值,πmax,m和πmin,m分别为节点m的允许压力上下限。
别为管道mn允许通过的天然气流量的最大值和最小值,πmax,m和πmin,m分别为节点m的允许压力上下限。
而由于能源中心的耦合,式(7)中节点净注入流量可表示为
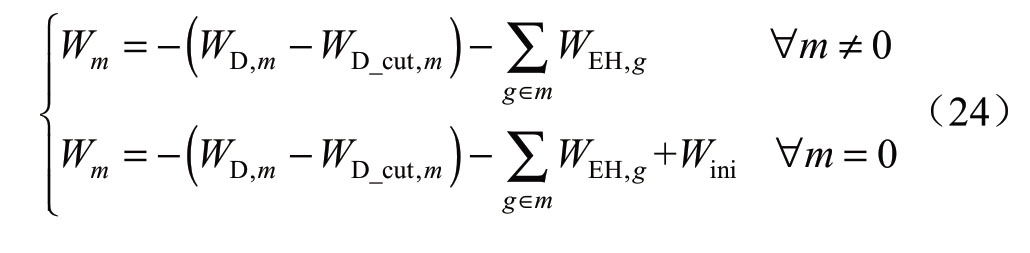
式中:m=0指配气子系统线路首端(即与上级气网交互节点);Wini为交互流量,为待求量;WEH为输入能源中心子系统的天然气流量需求;WD_cut为切负荷量,需满足可切量最大限值约束。
3)能源中心子系统状态量约束。
能源中心子系统主要满足能源输入-输出内部能流平衡约束,统一表达式如式(8)。具体内部多能源耦合建模视具体结构而定,常见典型结构模型可见文献[21-22]。
4)弃风弃光约束。
为最大可能消纳新能源,限制系统弃风弃光,模型增加约束:

式中:Rwind、RPV为系统可弃风、弃光容量,若需要求全额并网,则两参数为0。
3 模型求解
第2章构造的模型中,目标函数式(16)存在非光滑函数max{●},本文引入辅助变量Rs并构造线性约束进行等价处理[23],即

此外,对于气网潮流Weymouth方程的非凸特性,参考文献[26]引入离散变量进行分段线性化处理。至此,第2章构造的模型转为可有效求解的混合整数二阶锥规划模型,本文基于Matlab的Yalmip平台编程并调用Mosek求解器进行求解。
4 算例分析
4.1 基础数据
采用IEEE 33节点配电系统、7节点天然气系统以及4个能源中心构成区域IEGS进行仿真分析,结构如图3。IEEE 33节点配电系统的网架和负荷数据见文献[27-28],节点电压上下限设为0.93和1.05,并接入3个光伏电站和3个风电场,接入位置和功率预测值见附表A1。7节点天然气系统节点气压的上下限为1.3和0.1,管道数据见附表A2所示,节点负荷见附表A3。4个能源中心的设备组成以及各设备的能源转换效率和负荷水平见附表A4—A6[27]。目标函数各成本系数见附表A7。
不确定处理方面,考虑风、光、电/气/热负荷服从以预测值为均值的正态分布,采用拉丁超立方采样进行抽样场景生成,并采用同步回代消除算法将场景缩减为100个。目标函数中,权重系数α设为0.5,CVaR置信水平β=0.8。
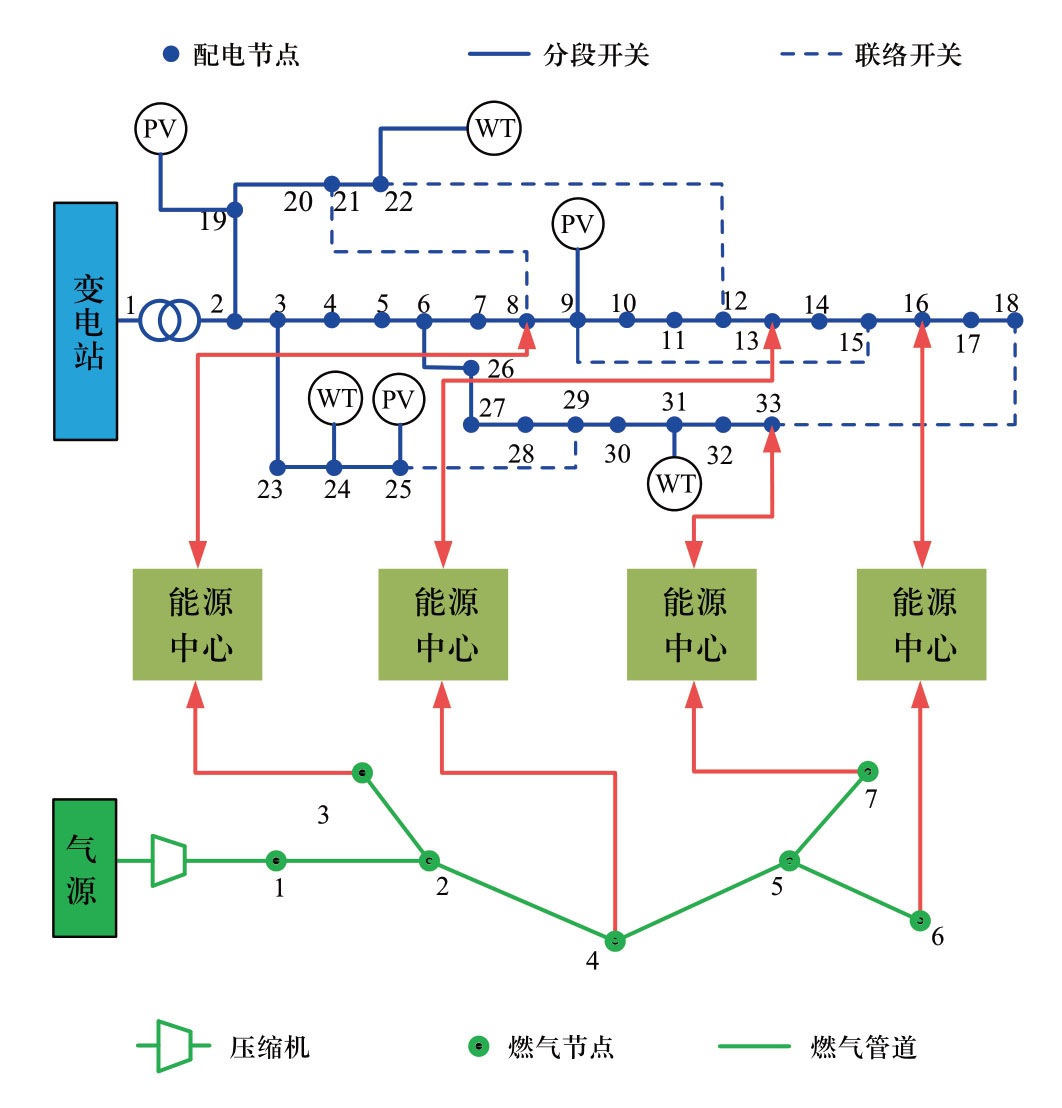
图3 仿真结构图
Fig.3 Schematic diagram of simulation system
4.2 重构前后成本优化结果分析
表1给出了考虑配电网重构前后线路开关的开合情况以及IEGS的用能调度情况。
表1 重构前后开关组合和成本构成
Table1 Switch combination and cost structure before and after reconstruction

由表1数据可知,优化重构后IEGS运行成本期望值、风险成本和计及CVaR的总成本分别下降了24.39、27.45和25.92美元,切负荷费用降低到0。算例中在经济目标驱使下,系统在其消纳能力内可消纳所有风光,故重构前后均没有出现弃风和弃光现象。
购电费用从116.24美元增加到了156.16美元,而购气费用从95.54美元降低到了80.40美元,计及CVaR的总成本下降百分比达到了9.46%,主要原因如下。
优化重构前由于负荷分布不均衡,电压约束受限,使得在负荷较重和分布式电源出力较低时,不得不切除部分负荷;此外,为了满足能源中心内电/气/热多能负荷需求,购买了价格相对较贵的天然气,提高了用能成本。而当考虑优化重构后,改善了传输功率分布,改善了节点电压(如图4所示,为随机抽取20个场景下配电网节点电压的分布),进而提高了配电网的供电能力。同时,由于重构后IEGS可以在系统安全情况下增大购电量从而降低了用气量,故在配电网重构后配气网络的气压节点也得到抬升(如图5所示,为随机抽取20个场景下节点气压的分布)而运行在更优的工况下,提升供气能力裕度,提高系统运行的可靠性。
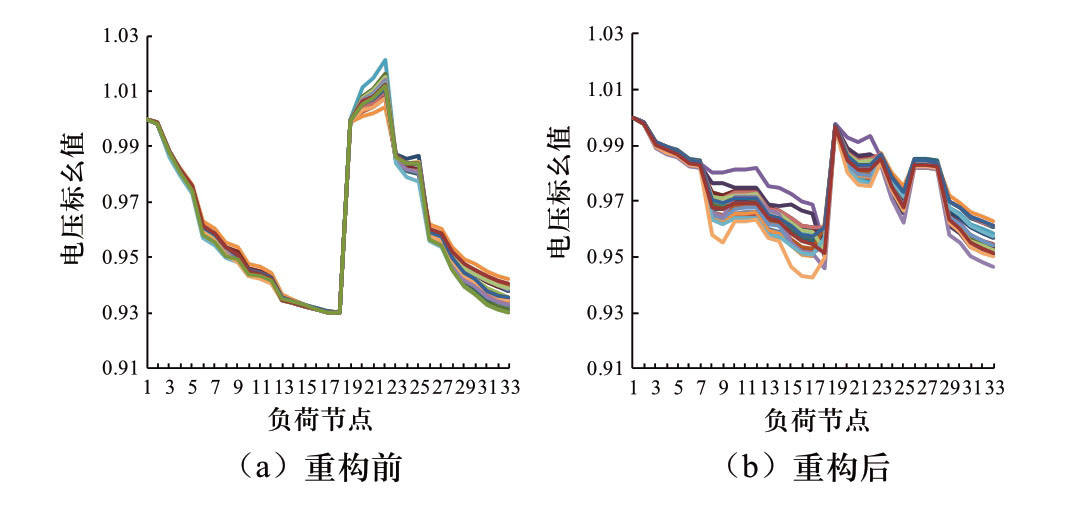
图4 重构前后节点电压分布
Fig.4 Power nodes voltage before and after reconstruction

图5 重构前后节点气压分布
Fig.5 Gas nodes voltage before and after reconstruction
4.3 计及CVaR与否对优化结果的影响
4.2节中,源-荷不确定参数设置基准为:风光出力的标准差为均值的0.2倍,冷热电负荷的标准差为均值的0.1倍。为分析不确定程度增大以及CVaR风险量化对优化结果的影响,本文在4.2节重构优化结果的基础上(即表1中重构后的优化结果,设为场景1),增设场景2(不考虑CVaR处理不确定性,将风光及负荷数据为其预测值)与场景3(CVaR处理不确定性,但不确定程度更大,风光出力和负荷的标准差设为相应均值的0.25倍)。
表2 不同场景下的结果对比分析
Table2 Comparative analysis of results in different scenarios

注:“—”表示无此类型数据。
表2中,以场景1为例,解释仿真结果中VaR以及CVaR值的含义。在场景1中,VaR的计算结果为250.70美元,表示在源-荷不确定影响下,有80%的概率(80%为仿真设置的置信水平β)可以保证IEGS运行成本不超过250.70美元。而CVaR计算结果为259.76美元,是指当IEGS运行成本出现了超过VaR值的情景时,其平均风险成本为259.76美元。
对比场景1和场景2,可知2个场景下获得的优化重构方案中开关组合是一样的,但考虑源-荷不确定后系统成本目标函数248.16美元,高于确定性方案下的成本优化结果。这是因为确定性方案下不能体现源荷不确定性给系统带来的风险损失,进而成本目标函数相对较低。
而对比场景1和场景3可知,当源-荷不确定程度增大时,系统运行风险程度增大,进而增加了系统的运行成本。此外,相比不考虑源-荷的不确定性、源-荷不确定程度较低2种情况,源-荷不确定程度增大时配网重构方案改变,说明IEGS需要更具鲁棒的重构结果来应对源-荷的波动,这也体现了考虑源-荷不确定性具有必要性。
4.4 置信水平对结果的影响
条件风险价值理论中,置信水平β可反映决策者对风险的把握程度。设β不同取值,分析对优化结果的影响,如图6所示。

图6 不同置信水平下的仿真结果
Fig.6 Simulation results under different confidence levels
图6中,风险成本和运行成本期望的值为乘以权重系数α=0.5后的数值。由图6可知,随着β的增加,运行成本期望值基本相同,但VaR和风险成本(CVaR值)有所增加。
β较低时,决策者采取较激进的策略,此时承担较大的风险,系统安全性较差;β较高时,系统对安全性要求增大,系统总的运行成本增大,系统的经济性变差,运行方案变得保守。决策人员可以根据地区源-荷历史数据信息,以及系统的实际情况调整置信水平。
5 结论
本文基于CVaR理论提出了计及源-荷不确定的综合能源系统中配电网网络优化重构模型。所提的模型考虑了供能终端多能耦合的趋势,以配电网便捷的重构操作,提升IEGS的综合运行能力。
1)配电网重构后,均衡了系统潮流分布,提高了系统供电能力,降低了切负荷量,并且由于能源中心与配气网的耦合,改善了配气网的流量分布从而提升了气网的传输裕度。
2)利用CVaR考虑了源-荷不确定性给优化运行带来的影响,使得IEGS中配电网重构结果更加合理并具有实际意义;根据自身对配电网重构风险厌恶水平的高低确定置信水平,均衡系统方案的经济性和安全性,适应不同的风险偏好。
本文研究为适应当前配电自动化、环网柜等自动化开关快速发展的背景,认为网络重构可根据系统运行的需要进行重构操作,且一个时间断面可以执行一次网络重构操作,因此考虑的仿真时段为一个时间断面,以点带面提升系统运行效果。下一步可针对日运行优化、多能源主体市场博弈下的IEGS配电网重构问题进行研究。
参考文献
[1]李立浧,张勇军,陈泽兴,等.智能电网与能源网融合的模式及其发展前景[J].电力系统自动化,2016,40(11):1-9.
LI Licheng,ZHANG Yongjun,CHEN Zexing,et al.Merger between smart grid and energy-net:mode and development prospects[J].Automation of Electric Power Systems,2016,40(11):1-9(in Chinese).
[2]乔铮,郭庆来,孙宏斌.电力-天然气耦合系统建模与规划运行研究综述[J].全球能源互联网,2020,3(1):14-26.
QIAO Zheng,GUO Qinglai,SUN Hongbin.Research survey on the modeling,planning and operational analysis of electricity-natural gas coupling system[J].Journal of Global Energy Interconnection,2020,3(1):14-26(in Chinese).
[3]LIANG J K,TANG W Y.Interval based transmission contingency-constrained unit commitment for integrated energy systems with high renewable penetration[J].International Journal of Electrical Power &Energy Systems,2020,119:105853.
[4]王瑞峰,王庆荣.基于改进双层聚类多目标优化的配电网动态重构[J].电力系统保护与控制,2019,47(21):92-99.
WANG Ruifeng,WANG Qingrong.Multi-objective optimization of dynamic reconfiguration of distribution network based on improved Bilayer clustering[J].Power System Protection and Control,2019,47(21):92-99(in Chinese).
[5]梁捷,李刚.基于节点特征分类的配电网重构辐射约束处理法[J].广东电力,2016,29(8):91-95.
LIANG Jie,LI Gang.Radial constraint handling method for reconfiguration of power distribution network based on feature classification of nodes[J].Guangdong Electric Power,2016,29(8):91-95(in Chinese).
[6]龚思宇,魏炜,徐元孚,等.面向分布式电源最大消纳的配电网重构[J].电力系统及其自动化学报,2017,29(3):7-11.
GONG Siyu,WEI Wei,XU Yuanfu,et al.Reconfiguration of distribution network for the maximum consumption of distributed generations[J].Proceedings of the CSU-EPSA,2017,29(3):7-11(in Chinese).
[7]刘路宁,彭春华,温泽之,等.基于配电网动态重构的分布式光伏消纳策略[J].电力自动化设备,2019,39(12):56-62.
LIU Luning,PENG Chunhua,WEN Zezhi,et al.Distributed photovoltaic consumption strategy based on dynamic reconfiguration of distribution network[J].Electric Power Automation Equipment,2019,39(12):56-62(in Chinese).
[8]高纯,于艾清,丁雨.基于改进布谷鸟算法的三相不平衡有源配电网重构[J].电力系统及其自动化学报,2020,32(9):143-150.
GAO Chun,YU Aiqing,DING Yu.Reconfiguration of unbalanced active distribution network based on improved Cuckoo algorithm [J].Proceedings of the CSU-EPSA,2020,32(9):143-150(in Chinese).
[9]吴在军,成晟,朱承治,等.基于线性近似模型的三相不平衡有源配电网重构[J].电力系统自动化,2018,42(12):134-141.
WU Zaijun,CHENG Sheng,ZHU Chengzhi,et al.Reconfiguration of unbalanced active distribution network based on linear approximation model[J].Automation of Electric Power Systems,2018,42(12):134-141(in Chinese).
[10]张今,耿光超,江全元,等.含柔性多状态开关的配电网多目标随机运行优化方法[J].高电压技术,2019,45(10):3140-3148.
ZHANG Jin,GENG Guangchao,JIANG Quanyuan,et al.Multi-objective stochastic operation optimization for distribution network with flexible multi-state switches[J].High Voltage Engineering,2019,45(10):3140-3148(in Chinese).
[11]靳小龙,穆云飞,贾宏杰,等.考虑配电网重构的区域综合能源系统最优混合潮流计算[J].电力系统自动化,2017,41(1):18-24.
JIN Xiaolong,MU Yunfei,JIA Hongjie,et al.Calculation of optimal hybrid power flow for integrated community energy system considering electric distribution network reconfiguration[J].Automation of Electric Power Systems,2017,41(1):18-24(in Chinese).
[12]周贤正,郭创新,董树锋,等.考虑配电网重构的城市多能源配电/气/热网扩展规划[J].电力系统自动化,2019,43(7):23-33.
ZHOU Xianzheng,GUO Chuangxin,DONG Shufeng,et al.Expansion planning of urban multi-energy electricitygas-heating distribution network incorporating electrical reconfiguration[J].Automation of Electric Power Systems,2019,43(7):23-33(in Chinese).
[13]董志辉,林凌雪.基于改进模糊C均值聚类时段划分的配电网动态重构[J].电网技术,2019,43(7):2299-2305.
DONG Zhihui,LIN Lingxue.Dynamic reconfiguration of distribution network based on improved fuzzy C-means clustering of time Division[J].Power System Technology,2019,43(7):2299-2305(in Chinese).
[14]葛鹏江,张树永,董晓晶,等.基于鲁棒优化的配网重构二阶锥规划模型[J].电力科学与技术学报,2018,33(4):50-57.
GE Pengjiang,ZHNAG Shuyong,DONG Xiaojing,et al.Distribution network reconfiguration model based on robust optimization[J].Journal of Electric Power Science and Technology,2018,33(4):50-57(in Chinese).
[15]李扬,韦钢,马钰,等.含电动汽车和分布式电源的主动配电网动态重构[J].电力系统自动化,2018,42(5):102-110.
LI Yang,WEI Gang,MA Yu,et al.Dynamic reconfiguration of active distribution network considering electric vehicles and distributed generations[J].Automation of Electric Power Systems,2018,42(5):102-110(in Chinese).
[16]易国伟,童小娇,周鹏,等.CVaR和EVaR安全运行风险管理下的电力系统经济调度[J].电力系统保护与控制,2016,44(8):49-56.
YI Guowei,TONG Xiaojiao,ZHOU Peng,et al.Power system economic dispatch under CVaR and EVaR security operation risk management[J].Power System Protection and Control,2016,44(8):49-56(in Chinese).
[17]张萌萌,董军.基于CVaR的灵活综合能源系统随机调度优化模型[J].全球能源互联网,2020,3(3):301-309.
ZHANG Mengmeng,DONG Jun.Stochastic scheduling model for flexible integrated energy system based on CVaR[J].Journal of Global Energy Interconnection,2020,3(3):301-309(in Chinese).
[18]赖晓文,马晓伟,白杨,等.基于混合整数二阶锥规划的动态无功优化方法[J].电力系统自动化,2017,41(17):37-42.
LAI Xiaowen,MA Xiaowei,BAI Yang,et al.Dynamic reactive power optimization method based on mixed integer second-order cone programming[J].Automation of Electric Power Systems,2017,41(17):37-42(in Chinese).
[19]GAN L W,LI N,TOPCU U,et al.Exact convex relaxation of optimal power flow in radial networks[J].IEEE Transactions on Automatic Control,2015,60(1):72-87.
[20]卢志刚,刘浩然,何良策.计及时段粒化的电-气综合能源系统低碳经济调度[J].全球能源互联网,2019,2(3):266-276.
LU Zhigang,LIU Haoran,HE Liangce.Low-carbon economic dispatch of integrated electricity and natural gas systems considering period granulation[J].Journal of Global Energy Interconnection,2019,2(3):266-276(in Chinese).
[21]蒋超凡,艾欣.面向工业园区的综合能源系统协同规划方法研究综述[J].全球能源互联网,2019,2(3):255-265.
JIANG Chaofan,AI Xin.Review on integrated energy system collaborative planning methods for industrial parks[J].Journal of Global Energy Interconnection,2019,2(3):255-265(in Chinese).
[22]王毅,张宁,康重庆.能源互联网中能量枢纽的优化规划与运行研究综述及展望[J].中国电机工程学报,2015,35(22):5669-5681.
WANG Yi,ZHANG Ning,KANG Chongqing.Review and prospect of optimal planning and operation of energy hub in energy Internet[J].Proceedings of the CSEE,2015,35(22):5669-5681(in Chinese).
[23]ROCKAFELLAR R T,URYASEV S.Optimization of conditional value-at-risk[J].The Journal of Risk,2000,2(3):21-41.
[24]KROKHMAL P,URYASEV T,PALMQUIST J.Portfolio optimization with conditional value-at-risk objective and constraints[J].The Journal of Risk,2001,4(2):43-68.
[25]LAVORATO M,FRANCO J F,RIDER M J,et al.Imposing radiality constraints in distribution system optimization problems[J].IEEE Transactions on Power Systems,2012,27(1):172-180.
[26]CORREA-POSADA C M,SÁNCHEZ-MARTÍN P.Integrated power and natural gas model for energy adequacy in shortterm operation[J].IEEE Transactions on Power Systems,2015,30(6):3347-3355.
[27]靳小龙,穆云飞,贾宏杰,等.面向最大供电能力提升的配电网主动重构策略[J].电工技术学报,2014,29(12):137-147.
JIN Xiaolong,MU Yunfei,JIA Hongjie,et al.An active reconfiguration strategy for distribution network based on maximum power supply capability[J].Transactions of China Electrotechnical Society,2014,29(12):137-147(in Chinese).
[28]KERSTING W H.Radial distribution test feeders[J].IEEE Transactions on Power Systems,1991,6(3):975-985.
附录A 算例参数设置
表A1 分布式电源接入情况
TableA1 Situation of distributed power access

表A2 天然气管网参数
TableA2 Parameters of natural gas network

表A3 天然气网络负荷
TableA3 Parameters of natural gas load

表A4 能源中心设备配置参数
TableA4 Configuration parameters of energy centers

注:CHP为热电联产设备,CAC为电制热设备,GB为燃气锅炉。
表A5 能源中心设备转换效率
TableA5 Conversion efficiency of energy centers

注:CHP为热电联产设备,CAC为电制热设备,GB为燃气锅炉。
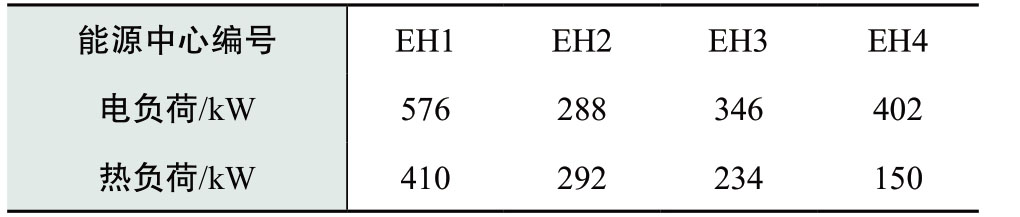
表A6 能源中心的电负荷和热负荷需求
TableA6 Electricity load and heat load demand of energy centers
表A7 目标函数成本系数
TableA7 Cost coefficients of objective function

收稿日期:2020-08-16;修回日期:2020-10-07。
Optimal Reconfiguration of Distribution Networks in Integrated Energy Systems Based on Conditional Value at Risk
CHEN Zexing1,ZHANG Yongjun2*,HUANG Yu1,QIN Yun1,CHEN Boda3,LIN Kaidong2
(1.Energy Research Institute of China Southern Power Grid Company Limited,Guangzhou 510663,Guangdong Province,China;2.Research Center of Smart Energy Technology,School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong Province,China;3.Guangzhou Power Supply Bureau of Guangdong Power Grid Corp.,Guangzhou 510620,Guangdong Province,China)
Abstract: The impact of the high multi-energy coupling of energy-utilization terminals must be considered during distribution-network reconfigurations.A rapid and flexible distribution-network reconfiguration enhances the optimization level of an integrated energy system.This paper presents an optimized operation model for the said reconfiguration of an integrated electric-power and natural-gas system (IEGS).From the cost-minimization perspective,the conditional value at risk (CVaR) can be used to quantify the operational risk posed by the IEGS source and load uncertainties.Subsequently,these risks can be converted to corresponding costs integrated within the objective function.Meanwhile,from the multi-energy couplingconstraint perspective,the distribution-network reconfiguration can be mapped onto the IEGS operation optimization model.Subsequently,the reconfiguration-switch control variables can be introduced into the power-flow model.Finally,the branch-breaking power-flow and radial distribution-network constraints can be constructed and linearized.The findings of this study reveal that reconfiguring the IEGS distribution network improves its operation capability.In addition,CVaR accounts for the source-load uncertainty,thereby improving the robustness of the IEGS distribution-network reconfiguration.
Keywords: integrated electric-power and natural-gas system;network reconstruction;conditional value at risk;source and load uncertainty
National Natural Science Foundation of China (51777077).
作者简介:

陈泽兴
陈泽兴(1992),男,博士,工程师,研究方向为能源互联网优化运行规划、电网规划运行,E-mail:chenzx3@csg.cn。
张勇军(1973),男,教授,博导,主要研究方向:主动配电网、无功电压控制、可靠性与规划,能源互联网运行控制等。通信作者,E-mail:zhangjun@scut.edu.cn。
(责任编辑 李锡)
