0 引言
当前,天然气和可再生能源在电力系统中大量使用[1-2]。天然气机组(natural gas units,NGUs)是电力系统中的电力供应商,同时也是天然气网络中的天然气消费者。另外,风能作为最重要的可再生能源之一,在过去几十年中经历了飞速发展[3]。但是,可再生能源固有的间歇性和波动性给电力和天然气互联系统(integrated electricity and natural gas system,IEGS)的联合运营带来了极大的不确定性,从而使其安全性易受影响[4]。因此,具有风电不确定性的IEGS协调调度问题具有重要的研究意义。
已经有学者研究机会约束的IEGS最优调度,以应对不确定风电预测误差所引起的运行风险[5]。在机会约束规划中,以概率表示的风险约束是针对物理约束(例如传输的电力流和气体流量),以一定的安全水平来限制不确定风电对线路过载或者管道过载的影响[6]。机会约束规划的解决方案包括场景近似[7],鲁棒优化[8],以及依赖于特定概率分布的分析形式[9]。但是,场景近似通常在计算上比较繁琐,总体上比较保守,而鲁棒优化与场景近似相比更为保守。如果不确定的参数不符合假定的概率分布,依赖特定分布的求解可能会导致结果不可靠[10]。机会约束的另一个挑战在于可再生能源具有不稳定的特性,难以获得大量的历史数据去刻画可再生能源的概率分布。为了解决这些缺点,有学者提出了基于分布鲁棒的机会约束(distributionally robust chance constraint,DRCC)。在DRCC中,不确定的约束需要在一定的概率下满足在模糊集中的所有分布。例如,文献[11]研究了DRCC基于不确定性参数的均值和协方差矩阵的矩模糊集,考虑风电不确定性对IEGS运行的影响。在文献[12]中,风能不确定性由Wasserstein模糊集描述,即在Wasserstein距离意义上围绕经验分布的候选分布。
上述研究的一个普遍假设是:电力和天然气系统由一个统一的公用事业公司运营,该公用事业公司可以使用集中模型来控制和运行这2个能源系统。但是,在大多数国家/地区(例如中国),这些能源系统是由不同公司运营的,他们的利益可能会相互冲突[13]。此外,公司希望将自己的信息保密,例如电力网络或天然气网络的详细信息,以及系统调度和市场参与者的数据,并且希望仅共享那些能够保证整个系统安全运行所需的最少信息量。因而,在随机的可再生能源大量接入下,如何保障电力和天然气网络能够仅共享有限的隐私数据就实现系统的优化运行是一个值得研究的现实问题。
学者们已经采用了各种方法来分解优化问题,例如Benders分解法[14]、拉格朗日松弛法[15]、增广拉格朗日松弛法[16]、最优条件分解法[17]、交替方向乘子法(alternating direction method of multipliers,ADMM)[13]等。其中,ADMM具有收敛性好、形式简单的优点,因此被广泛应用于分布式优化中。文献[18]利用标准ADMM方法和基于一致性的ADMM方法,以解决电-气互联的综合能源系统在有协调者和无协调者下的最优潮流问题,但没有考虑可再生能源不确定性的影响。由于交换隐私数据的局限性以及管理复杂模型的挑战,文献[19]利用ADMM,以较高的计算负担迭代求解电力系统子问题和天然气系统子问题。在文献[20]中,ADMM用于将互联的多区域IEGS的调度分解为各个区域协同的最优调度。通过分散式优化方案在不共享机密信息的情况下实现了互联区域的协调,保留各个区域决策的独立性和私密性,并且取得与IEGS集中式调度接近的结果。文献[21]构建了跨国的电-气-碳综合交易模型,并提出了基于ADMM的分散式跨国电力调度算法,从而保护了涉及国家的工业信息隐私。
本文使用松弛交替方向乘子法(relaxed alternating direction method of multipliers,RADMM)来解决含有不确定风功率的机会约束下的IEGS协同优化问题。本研究的贡献体现在三个方面:①建立了基于数据驱动的风电预测误差模糊集;②分析了不同的分布假设对电力和天然气互联系统运行风险成本的影响;③验证了RADMM相较于传统ADMM在收敛速度方面的优越性。
本文的其余部分安排如下。在第1章中,研究具有不确定风功率的IEGS的数学优化模型,并在不同的分布假设下构建机会约束和目标函数。在第2章中,在存在第三方可信任协调者的前提下,将RADMM方法用于电力和天然气的协同优化。第3章通过案例分析验证所提方法的有效性。第4章进行总结。
1 系统建模
1.1 风电不确定性
本文研究风电不确定性对电力和天然气耦合系统的影响。假设有nW个风力发电机组,它们的风电出力为 = W+ξ,可以认为由2部分组成,其中W是预测风机出力,ξ是不确定的预测误差,它的均值为µ0,协方差矩阵为Σ0。需要注意的是,日前调度是第一阶段的决策,在实时调度阶段,各个机组以参与因子的形式弥补预测误差以维持功率平衡。
= W+ξ,可以认为由2部分组成,其中W是预测风机出力,ξ是不确定的预测误差,它的均值为µ0,协方差矩阵为Σ0。需要注意的是,日前调度是第一阶段的决策,在实时调度阶段,各个机组以参与因子的形式弥补预测误差以维持功率平衡。
1.2 考虑机会约束的集中式电-气互联模型
假设电力需求dED ∈RnED和天然气需求dGD ∈RnGD是已知的,2个系统之间由消耗天然气来发电的NGUs作为桥梁。假设建立的电力系统模型具有nEN个节点,nEL条输电线路,nED个电力负荷和nE个火力机组(其中有nGE个NGU机组),而天然气系统包含nGN个节点,nGP条管道,nGD个天然气负荷,nG个天然气气井。对于电力流,仅考虑线性不计损耗的直流潮流,并使用潮流转移分布因子(power transfer distribution factor,PTDF)矩阵![]() 将电力流定义为节点注入功率的线性函数[19]。更具体地说,定义了3个矩阵
将电力流定义为节点注入功率的线性函数[19]。更具体地说,定义了3个矩阵![]() 和
和![]() 它们已经分别包含了火力机组、风电机组和电力需求到电力网络的映射。对于天然气系统,也需要引入适当的映射,气井
它们已经分别包含了火力机组、风电机组和电力需求到电力网络的映射。对于天然气系统,也需要引入适当的映射,气井![]() 天然气需求IGD ∈RnGN× nGD和NGU机组
天然气需求IGD ∈RnGN× nGD和NGU机组![]()
对于天然气系统潮流,出于计算可处理性的考虑,忽略了节点气体压力和管道填充量,采用可控流量模型[22]。具体来说,假设天然气流量是完全可控制的,并且受到每个管道最大容量的限制,该最大容量可以通过基于天然气系统中压力物理极限的事前分析来计算。参考文献[23],本文构建了稳态电-气互联潮流的优化模型。
集中优化问题旨在最小化运行电力和天然气系统的总成本,并考虑不确定的风力发电。因此,目标函数可以写为[23]
约束条件:

目标函数的意义是通过调节机组出力最小化模糊集中P任意分布F(ξ)导致的系统最大的风险成本。![]() 和
和![]() 分别是电力系统和天然气系统运行的二次成本函数,可以分别表示为
分别是电力系统和天然气系统运行的二次成本函数,可以分别表示为 ![]() 和
和![]() ΘE 和ΘG分别表示电力和天然气系统的可行集。
ΘE 和ΘG分别表示电力和天然气系统的可行集。
第一阶段的决策变量![]() 和
和![]() 分别表示电力生产,天然气生产,GNU的气体消耗和气体流量的日前调度。参考文献[24],本文采用了仿射策略(参与因子)的矩阵形式,以指定每个决策变量对每个风电场预测功率误差的纠正。因此,仿射策略
分别表示电力生产,天然气生产,GNU的气体消耗和气体流量的日前调度。参考文献[24],本文采用了仿射策略(参与因子)的矩阵形式,以指定每个决策变量对每个风电场预测功率误差的纠正。因此,仿射策略![]() 和
和![]() 对应电力生产,天然气生产,GNU的气体消耗和气体流量的实时纠正动作,以弥补预测误差造成的供需不平衡。约束(4)用来描述电力系统和天然气系统之间的耦合约束,对角矩阵
对应电力生产,天然气生产,GNU的气体消耗和气体流量的实时纠正动作,以弥补预测误差造成的供需不平衡。约束(4)用来描述电力系统和天然气系统之间的耦合约束,对角矩阵![]() 包含GNU的功率转换因子,其中非GNU的对应元素为0。
包含GNU的功率转换因子,其中非GNU的对应元素为0。
1.2.1 电力系统约束
式(2)中的可行集ΘE包含等式和不等式约束以及电力系统运行的机会约束。电力系统的直流潮流约束为
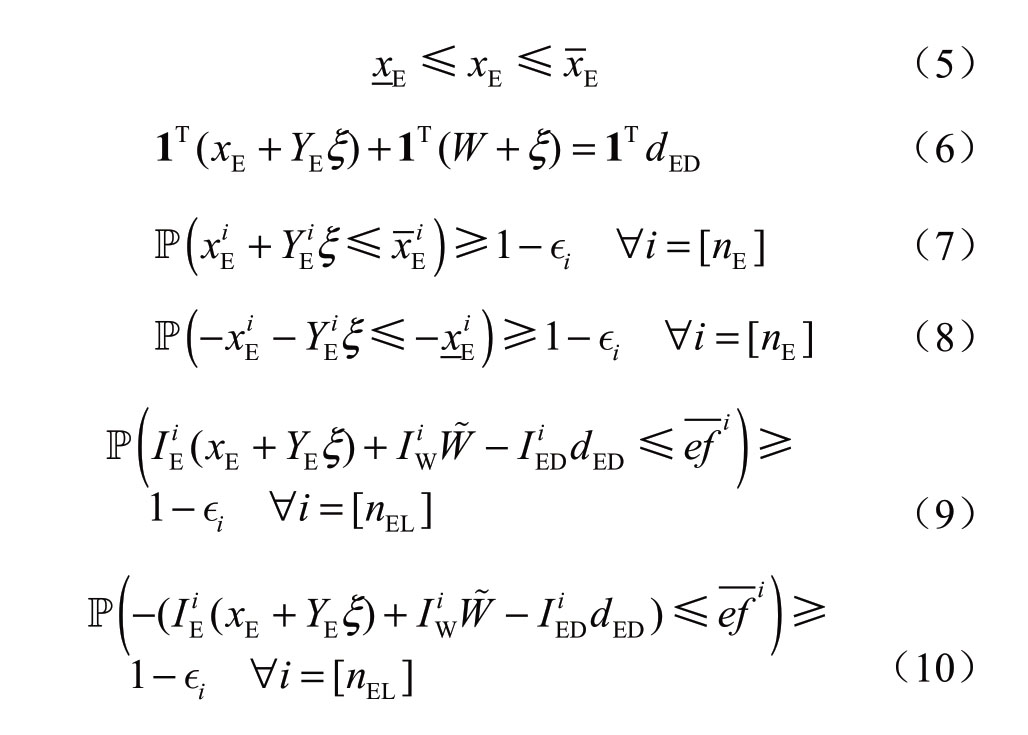
式中:[nE]、[nEL]分别表示所有火力机组组成的集合、所有电力线路组成的集合。在本文中,1表示合适维度的全部元素为1的列向量。例如,1T dED可以表示dED所有元素的和,即总的电力负荷。另外,在本文中,矩阵或向量的上标i表示其第i行向量或元素。具体来说,约束(5)表示火力机组第一阶段的出力限制, 和
和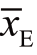 分别是发电功率的下限、上限。约束(6)确保日前和实时阶段的功率平衡。实时机组出力和线路潮流的容量受以下机会约束限制:(7),(8)和(9),(10)。
分别是发电功率的下限、上限。约束(6)确保日前和实时阶段的功率平衡。实时机组出力和线路潮流的容量受以下机会约束限制:(7),(8)和(9),(10)。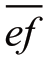 表示电力线路传输有功功率上限。
表示电力线路传输有功功率上限。
1.2.2 天然气系统约束
类似地,式(3)中的可行集ΘG包含与天然气系统运行相关的一组约束。
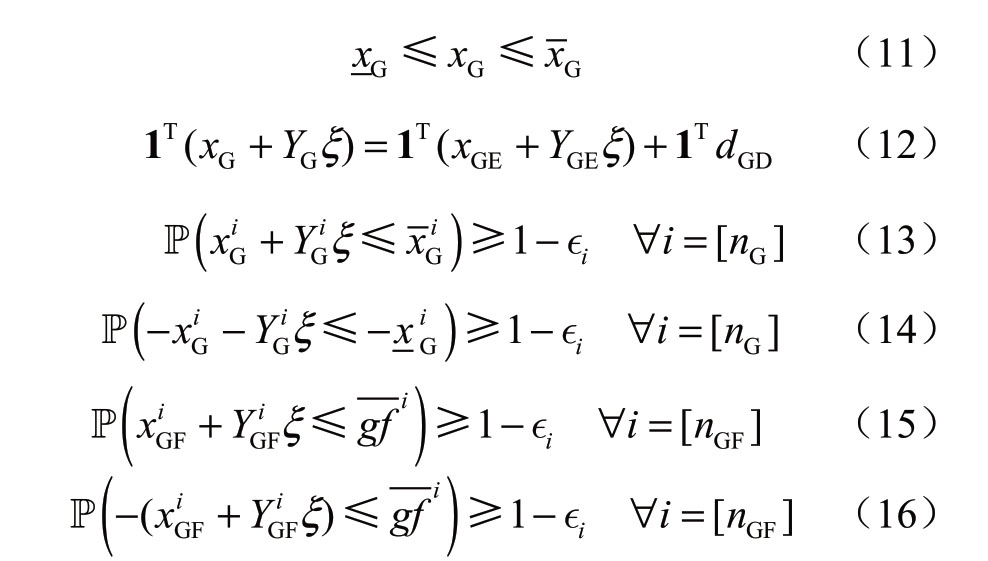
式中:[nG]、[nGF]分别表示所有天然气气井组成的集合、所有天然气管道组成的集合。类似地,约束(11)限制了天然气气井的下限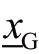 和上限
和上限 。约束(12)确保日前和实时阶段的天然气生产消耗平衡。实时天然气产量和管道流量由以下机会约束限制:(13)、(14)和(15)、(16)。
。约束(12)确保日前和实时阶段的天然气生产消耗平衡。实时天然气产量和管道流量由以下机会约束限制:(13)、(14)和(15)、(16)。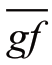 表示管道传输的天然气流量上限。
表示管道传输的天然气流量上限。
1.2.3 耦合约束
等式约束(17)将天然气消耗和NGU的电力出力联系起来。若令E=[xE,YE]、GE=[xGE,YGE],那么式(4)电-气的耦合约束可直接表示为
1.3 机会约束转换
首先,考虑将每一个来自式(7)—(10)和(13)—(16)的机会约束i表示为通用形式:
其中,矩阵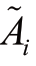 表示机会约束的不确定部分,而bi表示确定的部分,NI表示总的机会约束的个数。
表示机会约束的不确定部分,而bi表示确定的部分,NI表示总的机会约束的个数。
针对风电预测误差不确定性的分布鲁棒、对称分布鲁棒或高斯分布这3种假设情况,本文给出了对应的机会约束的转化形式,以便于求解。
1)分布鲁棒机会约束。
根据观察到的有限数量的历史样本,可以计算其真实分布F(ξ)的经验均值![]() 和协方差
和协方差![]() 假设随机变量ξ的真实均值和协方差可以从现有历史数据的经验均值
假设随机变量ξ的真实均值和协方差可以从现有历史数据的经验均值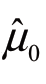 和协方差
和协方差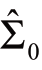 准确获得,则可以定义模糊集D为[25]
准确获得,则可以定义模糊集D为[25]
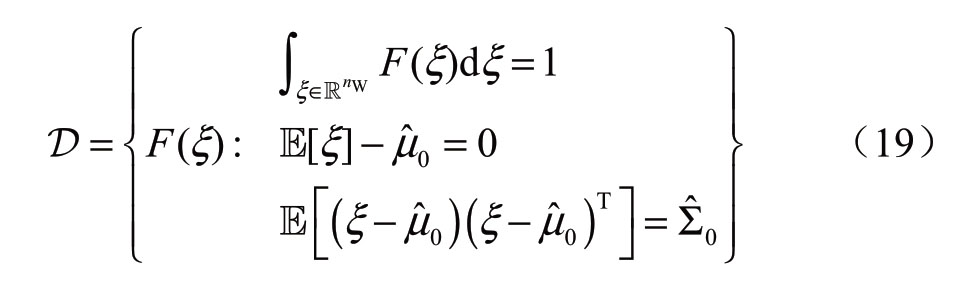
其中RnW是随机变量ξ支撑集。
若随机变量ξ的分布属于模糊集D,为了符号上的方便,以更加一般的形式来描述分布鲁棒机会约束(18):
式(20)可以等效为二阶锥规划,对于任意的ε ∈(0,1),可以得到
其中有
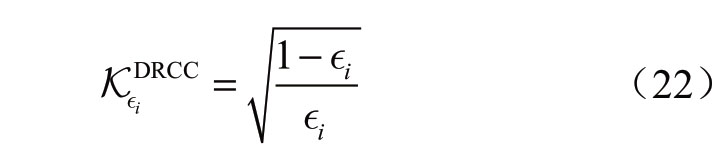
该推导遵循文献[26]中给出的Chebyshev不等式的一种变体,用于一般的分布鲁棒机会约束。对于均值为µ、方差为σ2 的随机变量X,可以得到![]() 对于任意的0 1≤ ≤δ 都成立。根据文献[27],存在一个属于模糊集D的分布使得不等式紧致。这样,如果令那么,式(20)可以用式(21)等效替代。
对于任意的0 1≤ ≤δ 都成立。根据文献[27],存在一个属于模糊集D的分布使得不等式紧致。这样,如果令那么,式(20)可以用式(21)等效替代。
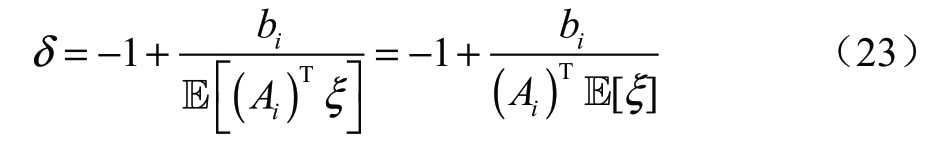
2)对称分布鲁棒机会约束。
如果风功率误差的概率分布是对称的,则对称分布鲁棒机会约束(symmetrical distributionally robust chance constraint,S-DRCC)下的系数Kεi可以写为[28]
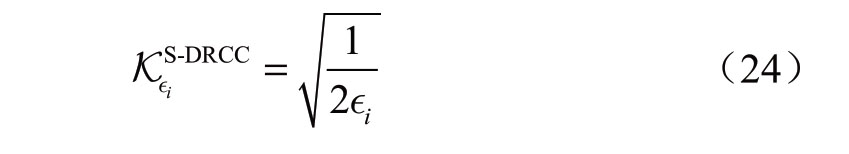
3)高斯分布机会约束。
如果假设风功率预测误差服从高斯分布[29],则高斯机会约束(Gaussian chance constraint,GCC)下的变换系数Kεi可以写为
其中ψ(x)是高斯分布的累积分布函数。
对于风功率误差服从分布鲁棒、对称分布鲁棒或高斯分布这3种假设情况,通过系数Kεi控制不同分布假设下机会约束的鲁棒特性。不同分布假设下的系数Kεi随置信水平1-εi变化的趋势如图1所示。
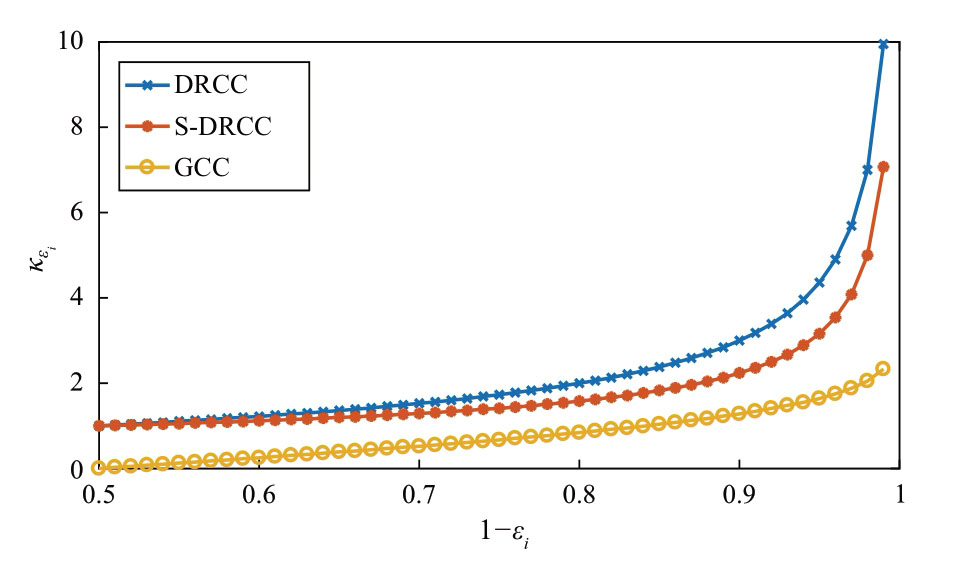
图1 系数Kεi随置信平1-εi的变化情况
Fig.1 Change of Kεi with confidence level 1-εi
可以发现,对于一个特定的εi,系数![]() 比相应的
比相应的![]() 和
和![]() 要大。例如,当εi为0.05时,对于高斯分布、对称分布鲁棒和分布鲁棒,Kεi分别为1.645、3.162 3和4.358 9。这意味着分布鲁棒的鲁棒性最强,它是以系统总运行成本为代价,对所有的分布(包括不对称的分布)具有鲁棒性。
要大。例如,当εi为0.05时,对于高斯分布、对称分布鲁棒和分布鲁棒,Kεi分别为1.645、3.162 3和4.358 9。这意味着分布鲁棒的鲁棒性最强,它是以系统总运行成本为代价,对所有的分布(包括不对称的分布)具有鲁棒性。
1.4 目标函数转换
关于式(1)中的目标函数,本文以最小化D中所有分布的最坏情况下预期风险成本为目标,将其表示为
式中:CE (x E,YE,ξ)和CG (xG,YG,ξ)分别是电力系统和天然气系统运行的二次成本函数;GE(E)和GG(G)分别是电力系统和天然气系统的最大风险成本,可以表示为
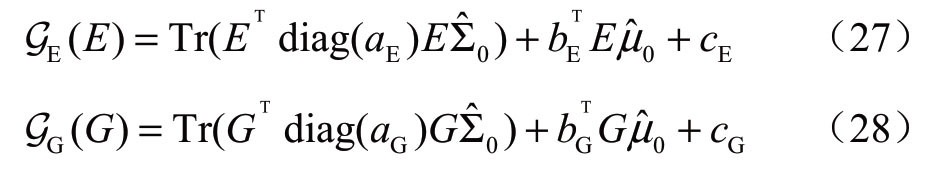
式中:aE、bE、cE分别是电力系统火力机组的二次函数成本的相关系数;aG、bG、cG分别是天然气气井的二次函数成本的相关系数。运算Tr(A)表示求取矩阵A的迹。diah(a)表示一个以a的所有元素为对角元素的对角矩阵。
2 基于松弛交替乘子法的分布式优化
在很多国家(包括中国),天然气运营商(gas operator,GO)和电力运营商(electricity operator,EO)由不同的主体拥有,如何协同合作降低总运营成本对于提升整体社会福利具有显著意义。ADMM是一种解决可分解凸优化问题的简单方法,尤其在解决大规模问题上卓有成效,利用ADMM算法可以将原问题的目标函数等价分解成若干个可求解的子问题,然后并行求解每一个子问题,最后协调子问题的解得到原问题的全局解。由此可见,ADMM的算法原理是适用于电-气互联系统的协同优化的。为了进一步提升ADMM的收敛速率,已经有学者引入松弛项,构建了RADMM,应注意,当松弛项因子α设置为0.5时,RADMM即为标准ADMM,具体的收敛证明可见文献[30]。
本章描述如何将RADMM用于存在第三方协调者(coordination operator,CO)的情况(如图2所示)。在这种情况下,由于电力和天然气网络的协同运行主要由CO完成,因此必须在上级CO和下级GO/EO之间建立通信通道。

图2 电-气互联网络分布式运行
Fig.2 Distributed synergistic operation of the electricity and gas networks
参照文献[30]的步骤,针对机会约束下电-气互联网络的协同优化问题进行求解。对约束(17)进行拉格朗日松弛后,式(1)的增广拉格朗日对偶可以表示为
式中:λ是拉格朗日乘子;ρ >0是惩罚因子。
在基于有协调者IEGS优化运行中,EO和GO的局部优化问题以串行方式进行,并通过CO进行协调,详细步骤如下。
1)电力网络优化问题。
通过将耦合约束(17)添加到电力成本函数中,电力网络的优化子问题可以构造为
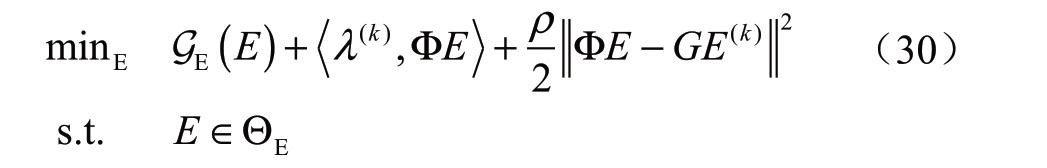
求解得到E(1)k+。
2)天然气网络优化问题。
天然气网络优化子问题可以构造为
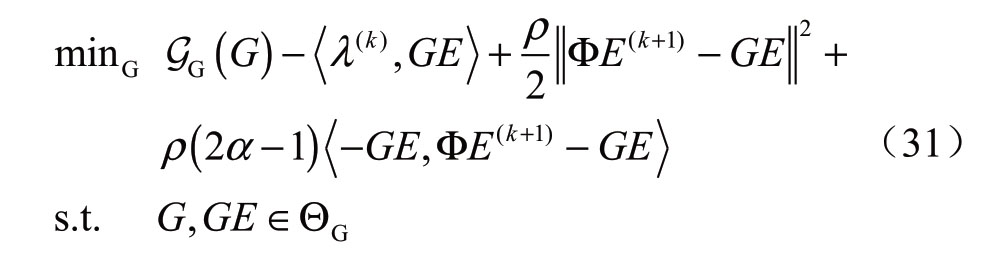
求解得到GE(1)k+。
3)协调者优化问题。
CO通过收集到的电力网络子问题的求解信息和天然气网络的求解信息进行协调:
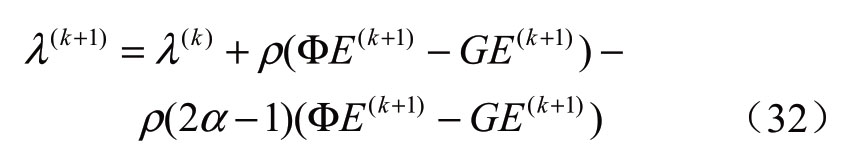
求解得到λ(1)k+。
算法的收敛性通过判断原始残差![]() 和对偶残差
和对偶残差 ![]() 是否达到设定精度给出。如果在k+1次迭代计算时,
是否达到设定精度给出。如果在k+1次迭代计算时,![]() 其中η是一个较小的精度衡量指标,或者迭代达到k次就输出结果,算法结束。否则,设置(k) ← (k+ 1),EO和GO继续迭代计算直到满足终止条件。类似的过程也可以参照文献[18,23],但它们都是使用具有协调者的标准ADMM方法实现的。
其中η是一个较小的精度衡量指标,或者迭代达到k次就输出结果,算法结束。否则,设置(k) ← (k+ 1),EO和GO继续迭代计算直到满足终止条件。类似的过程也可以参照文献[18,23],但它们都是使用具有协调者的标准ADMM方法实现的。
3 案例分析
3.1 案例数据
将具有12个节点的天然气网络和IEEE 24节点可靠性测试系统的集成系统[31]用于本文的案例研究。通过连接6个风电场到电力网络的1、2、11、12、12和16母线来扩展该电-气互联网络,所有风电场的容量均为250 MW。案例分析中,使用2012—2013年澳大利亚东南部6个风电场的相对风电输出数据,按照文献[32]中的方法构造预测风功率W和预测误差ξ。在本文中,所有分布鲁棒机会约束的置信水平εi都设置为相同的值。本章所有优化问题是由Gurobi 8.1.0求解的。对于所研究的系统,给出设置:η=0.01,ρ=0.001,K=1000。
3.2 不同分布特性假设对系统运行成本的影响
为了评估电-气互联能源系统的真实运行情况,本研究基于100个耦合数据集 ![]() 评估系统的调度成本和机会约束的违反概率。数据集
评估系统的调度成本和机会约束的违反概率。数据集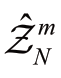 是包含N个独立同分布(i.i.d.)样本数据的训练数据集,
是包含N个独立同分布(i.i.d.)样本数据的训练数据集,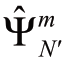 是包含N'个样本的测试集。m表示第m次仿真。在此研究中设置了N=N'=100,且仿真次数设置为100次。
是包含N'个样本的测试集。m表示第m次仿真。在此研究中设置了N=N'=100,且仿真次数设置为100次。
首先利用集中式求解分析εi 对不同分布特性优化结果的影响。使用训练集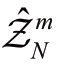 估计风功率误差的均值和协方差矩阵,并优化得出机组的日前调度计划和应对不确定误差的仿射策略。然后在此基础上,使用测试数据集
估计风功率误差的均值和协方差矩阵,并优化得出机组的日前调度计划和应对不确定误差的仿射策略。然后在此基础上,使用测试数据集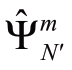 进行实时模拟,并计算违反约束的概率。在使用了全部100个耦合数据集之后,使用经验违反概率来比较计算不同机会约束下应对测试集的表现效果:
进行实时模拟,并计算违反约束的概率。在使用了全部100个耦合数据集之后,使用经验违反概率来比较计算不同机会约束下应对测试集的表现效果:

式中: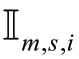 是指标函数,如果单个机会约束i在第m次仿真下的第s个场景中被违反了,就取值为1,反之则为0。
是指标函数,如果单个机会约束i在第m次仿真下的第s个场景中被违反了,就取值为1,反之则为0。
经验调度成本计算为
式中:Cm是基于利用训练集 得到的决策信息,然后根据测试集
得到的决策信息,然后根据测试集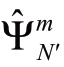 计算得到的调度成本。
计算得到的调度成本。
图3和图4分别给出了不同置信水平1-εi的不同机会约束变换下的经验成本和违反概率。图3显示不同分布特性下,系统的经验运行成本随置信水平1-εi的变化趋势,对应的经验违反约束的概率如图4所示。可以看到,由于DRCC的鲁棒性最强,同样风险水平下的经验违反概率是最小的,但与此同时,这会导致系统的运行成本最高。另外,当风险水平εi 较小时,进一步减少风险水平就会导致极大地增加系统的运行成本。
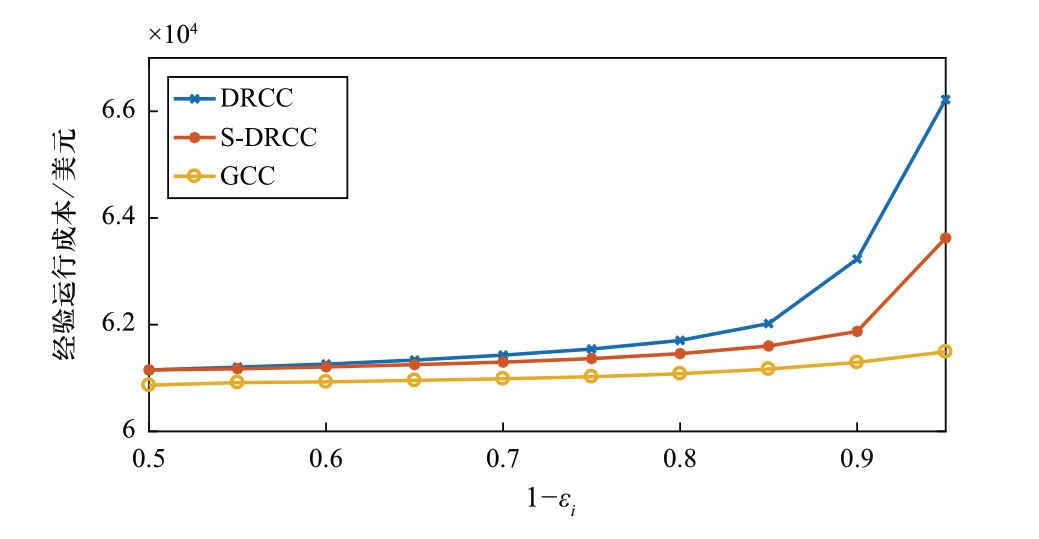
图3 不同置信水平1-εi的经验运行成本
Fig.3 Empirical dispatch cost with different confidence level 1-εi
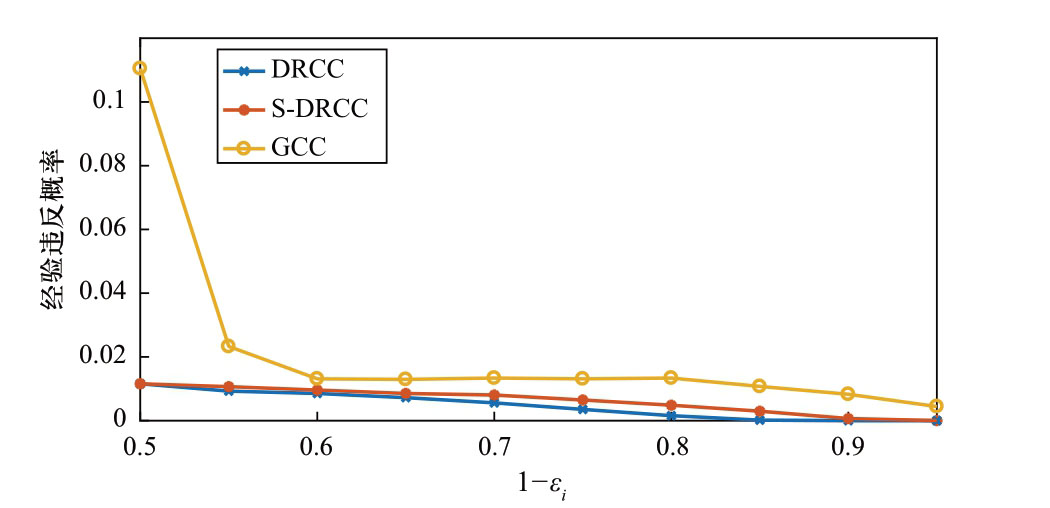
图4 不同置信水平1-εi的经验违反概率
Fig.4 Empirical violation probability with different confidence level 1-εi
3.3 电-气协同优化
本节考虑电-气互联系统协同优化的场景,基于分布鲁棒机会约束规划的IEGS测试松弛交替乘子方法的性能。表1给出了使用不同松弛因子α时,RADMM算法在系统成本、迭代次数和CPU时间方面的对比情况。Nit是需要的迭代次数。
表1 松弛交替乘子法的收敛效果
Table1 Convergence performances of RADMM
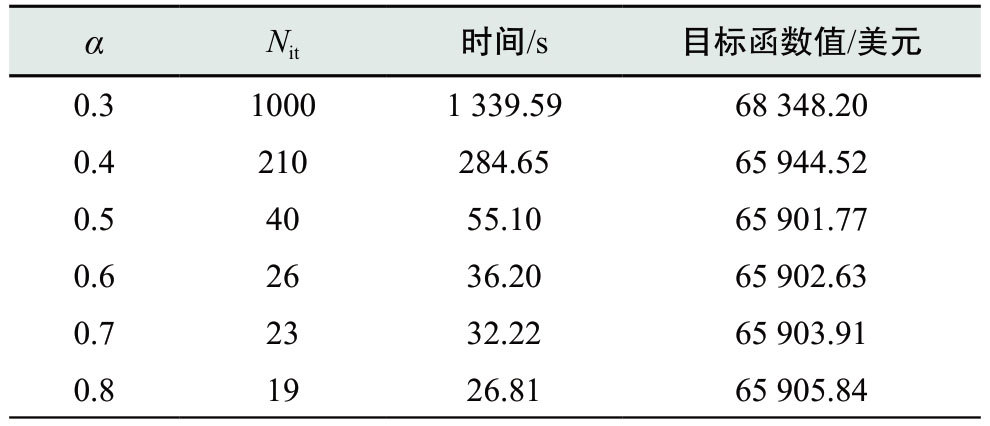
可以看出,松弛因子α的引入会影响收敛速度。当α =0.5时,RADMM即为传统ADMM,在该设置下,RADMM方法需要40次迭代,花费55.10 s的计算时间达到收敛条件。α >0.5时,RADMM具有比传统ADMM更快的收敛速度。当α >0.5时,目标函数的最大值(当α =0.8时)相对于集中式优化得到的结果(65 903美元)的误差的数量级是10-5,仍处于可接受的精度水平。因此,这些结果表明使用稍微复杂一些的RADMM代替经典ADMM对于求解IEGS问题是合理的。
图5表示了RADMM的原始残差和对偶残差的迭代变化。可以发现,原始残差的收敛速度都比对偶残差慢,因此终止条件由原始残差确定。
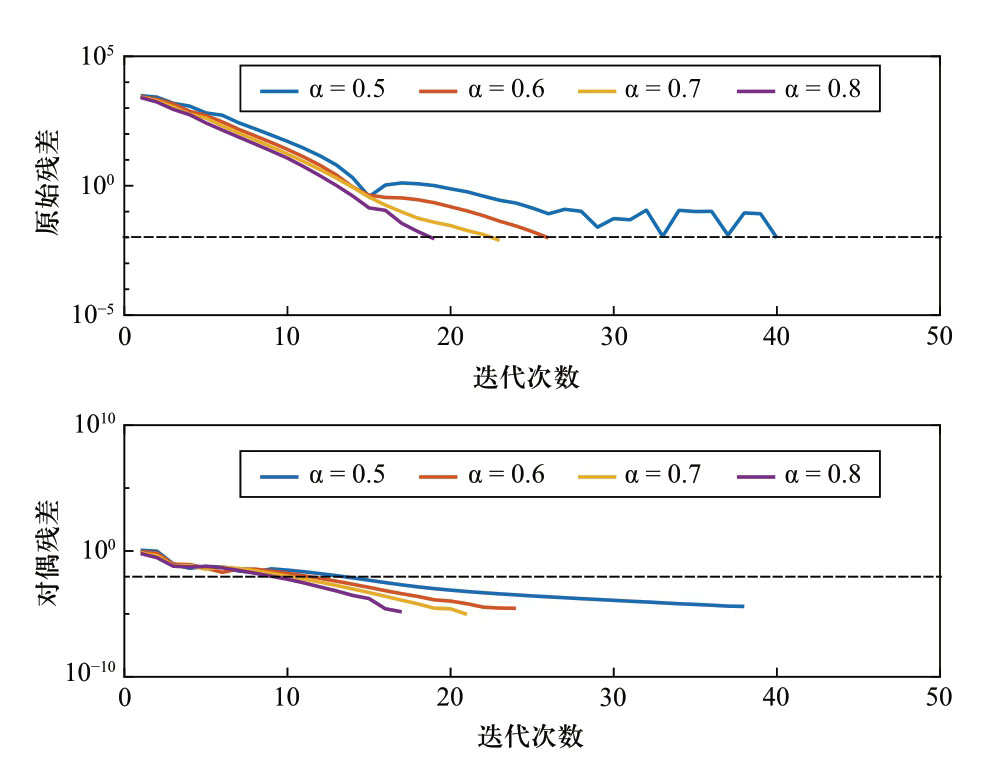
图5 RADMM计算的原始残差和对偶残差的迭代值
Fig.5 Iterative values of the primal and dual residuals of RADMM
4 结论
本文采用基于分布鲁棒机会约束的方法,通过数据驱动,得到风电分布的模糊集,并且基于不同的分布假设将机会约束和目标函数转化为易于求解的形式。在有第三方可信任协调者的前提下,本文给出了基于松弛交替乘子法的求解步骤。仿真结果表明,分布鲁棒优化相比较于传统的随机优化更适合电-气互联网络应对不确定风电对耦合系统的运行风险。另外,相比较于传统交替乘子法,松弛交替乘子法能够以更小的迭代次数达到同等的收敛精度。
参考文献
[1]乔铮,郭庆来,孙宏斌.电力-天然气耦合系统建模与规划运行研究综述[J].全球能源互联网,2020,3(1):14-26.
QIAO Zheng,GUO Qinglai,SUN Hongbin.Research survey on the modeling,planning and operational analysis of electricity-natural gas coupling system[J].Journal of Global Energy Interconnection,2020,3(1):14-26(in Chinese).
[2]DABABNEH F,LI L.Integrated electricity and natural gas demand response for manufacturers in the smart grid[J].IEEE Transactions on Smart Grid,2019,10(4):4164-4174.
[3]GUO Y,BAKER K,DALL’ANESE E,et al. name="ref4" style="font-size: medium; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em; color: rgb(0, 0, 0); font-family: SimSun; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: 2; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration-style: initial; text-decoration-color: initial;">[4]FARROKHIFAR M,NIE Y H,POZO D.Energy systems planning:a survey on models for integrated power and natural gas networks coordination[J].Applied Energy,2020,262:114567.
[5]WU G,XIANG Y,LIU J,et al.Chance-constrained optimal dispatch of integrated electricity and natural gas systems considering medium and long-term electricity transactions[J].CSEE Journal of Power and Energy Systems,2019,5(3):315-323.
[6]BAKER K,BERNSTEIN A.Joint chance constraints in AC optimal power flow:improving bounds through learning[J].IEEE Transactions on Smart Grid,2019,10(6):6376-6385.
[7]CAMPI M C,GARATTI S,PRANDINI M.The scenario approach for systems and control design[J].Annual Reviews in Control,2009,33(2):149-157.
[8]MARGELLOS K,GOULART P,LYGEROS J.On the road between robust optimization and the scenario approach for chance constrained optimization problems[J].IEEE Transactions on Automatic Control,2014,59(8):2258-2263.
[9]BIENSTOCK D,CHERTKOV M,HARNETT S.Chanceconstrained optimal power flow:risk-aware network control under uncertainty[J].SIAM Review,2014,56(3):461-495.
[10]LI B W,JIANG R W,MATHIEU J L.Distributionally robust risk-constrained optimal power flow using moment and unimodality information[C]//2016 IEEE 55th Conference on Decision and Control (CDC).December 12-14,2016,Las Vegas,NV,USA.IEEE,2016:2425-2430.
[11]FANG X,CUI H T,YUAN H Y,et al.Distributionally-robust chance constrained and interval optimization for integrated electricity and natural gas systems optimal power flow with wind uncertainties[J].Applied Energy,2019,252:113420.
[12]WANG C,GAO R,WEI W,et al.Risk-based distributionally robust optimal gas-power flow with Wasserstein distance[J].IEEE Transactions on Power Systems,2019,34(3):2190-2204.
[13]WANG L X,ZHENG J H,JING Z X,et al.Individual-based distributed parallel optimization for operation of integrated energy systems considering heterogeneous structure[J].International Journal of Electrical Power &Energy Systems,2020,118:105777.
[14]ZHOU H S,ZHENG J H,LI Z G,et al.Multi-stage contingency-constrained co-planning for electricity-gas systems interconnected with gas-fired units and power-to-gas plants using iterative Benders decomposition[J].Energy,2019,180:689-701.
[15]BUKOWSKI S,TABAREZ J,RANADE S J,et al.Decentralized energy scheduling of distributed resources using Lagrangian relaxation[C]//2016 North American Power Symposium (NAPS).September 18-20,2016,Denver,CO,USA.IEEE,2016:1-5.
[16]BISKAS P N,N G.Co-optimization of electricity day-ahead market and steady-state natural gas system using Augmented Lagrangian[C]//11th International Conference on the European Energy Market (EEM14).May 28-30,2014,Krakow,Poland.IEEE,2014:1-6.
[17]HUANG J B,LI Z G,WU Q H.Coordinated dispatch of electric power and district heating networks:a decentralized solution using optimality condition decomposition[J].Applied Energy,2017,206:1508-1522.
[18]WEN Y F,QU X B,LI W Y,et al.Synergistic operation of electricity and natural gas networks via ADMM[J].IEEE Transactions on Smart Grid,2018,9(5):4555-4565.
[19]HE C,WU L,LIU T Q,et al.Robust co-optimization scheduling of electricity and natural gas systems via ADMM[J].IEEE Transactions on Sustainable Energy,2017,8(2):658-670.
[20]QI F,SHAHIDEHPOUR M,WEN F S,et al.Decentralized privacy-preserving operation of multi-area integrated electricity and natural gas systems with renewable energy resources[J].IEEE Transactions on Sustainable Energy,2020,11(3):1785-1796.
[21]杨青润,丁涛,曾子彧,等.考虑电-气-碳综合交易的跨国电网分散式电力调度—以规划的东北亚跨国电网为例[J].全球能源互联网,2019,2(6):589-597.
YANG Qingrun,DING Tao,ZENG Ziyu,et al.Distributed power dispatch of transnational power grids considering power-gas-carbon joint transactions:an example of planned Northeast Asian power grid[J].Journal of Global Energy Interconnection,2019,2(6):589-597(in Chinese).
[22]WANG C,WEI W,WANG J H,et al.Strategic offering and equilibrium in coupled gas and electricity markets[J].IEEE Transactions on Power Systems,2018,33(1):290-306.
[23]ORDOUDIS C.Market-based approaches for the coordinated operation of electricity and natural gas systems[D].Technical University of Denmark,2018.
[24]JABR R A.Adjustable robust OPF with renewable energy sources[J].IEEE Transactions on Power Systems,2013,28(4):4742-4751.
[25]ZHANG Y L,SHEN S Q,MATHIEU J L.Distributionally robust chance-constrained optimal power flow with uncertain renewables and uncertain reserves provided by loads[J].IEEE Transactions on Power Systems,2017,32(2):1378-1388.
[26]WAGNER M R.Stochastic 0-1 linear programming under limited distributional information[J].Operations Research Letters,2008,36(2):150-156.
[27]BERTSIMAS D,POPESCU I.Optimal inequalities in probability theory:a convex optimization approach[J].SIAM Journal on Optimization,2005,15(3):780-804.
[28]CALAFIORE G C,GHAOUI L E.On distributionally robust chance-constrained linear programs[J].Journal of Optimization Theory and Applications,2006,130(1):1-22.
[29]FANG X,HODGE B M,JIANG H G,et al.Decentralized wind uncertainty management:Alternating direction method of multipliers based distributionally-robust chance constrained optimal power flow[J].Applied Energy,2019,239:938-947.
[30]BASTIANELLO N,TODESCATO M,CARLI R,et al.Distributed optimization over lossy networks via relaxed peaceman-rachford splitting:a robust ADMM approach [C]//2018 European Control Conference (ECC).June 12-15,2018,Limassol,Cyprus.IEEE,2018:477-482.
[31]ORDOUDIS C,PINSON P,MORALES J M.An integrated market for electricity and natural gas systems with stochastic power producers[J].European Journal of Operational Research,2019,272(2):642-654.
[32]DOWELL J,PINSON P.Very-short-term probabilistic wind power forecasts by sparse vector autoregression[J].IEEE Transactions on Smart Grid,2016,7(2):763-770.
收稿日期:2020-07-24;修回日期:2020-09-22。
Synergistic Economic Dispatch of Wind-power-integrated Electricity and Natural Gas Systems
QIAN Tong,CHEN Xingyu,ZHANG Wenhao,TANG Wenhu*
(School of Electric Power Engineering,South China University of Technology,Guangzhou 510640,Guangdong Province,China)
Abstract: The gradually increasing in the number of naturalgas units has increased the number of interconnected power and natural-gas networks.Accordingly,synergistic operation between these networks has assumed greater importance.In addition,the simultaneous integration of renewable energy in these systems poses challenges pertaining to the economically viable and safe operation of these systems.This paper presents a distributionally robust chance constraints (DRCC) method to mitigate the operational risks posed by the uncertainty of wind-energy generation to the interconnected system.Using a style="font-size: medium; text-align: justify; text-indent: 0px; line-height: 1.8em; margin: 0.5em 0em; color: rgb(0, 0, 0); font-family: SimSun; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: 2; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration-style: initial; text-decoration-color: initial;">Keywords: electricity-gas network;distributionally robust optimization;wind power;synergy;relaxed alternating direction method of multipliers
National Key Research and Development Program of China (2018YFE0208400).
作者简介:

钱瞳
钱瞳(1992),男,博士,研究方向为分布式协调控制运行,多代理系统,微电网控制运行。
陈星宇(1997),男,硕士研究生,研究方向为最大功率跟踪,信息物理融合系统,灾害下主动调度。
张文浩(1994),男,博士研究生,研究方向为微电网控制运行,信息物理融合系统。
唐文虎(1974),男,教授,IEEE高级会员,IET会士,华南理工大学电力学院院长,研究方向为可再生能源消纳,状态监测和故障诊断,弹性电网。通信作者,E-mail:wenhutang@scut.edu.cn。
(责任编辑 李锡)
