0 引言
近年来,我国分布式电源在电网中的渗透率不断上升,但由于分布式电源出力的随机性、间歇性等特点,局限了其在电网系统中的推广与应用[1]。储能系统因具有平抑可再生能源功率波动、提升新能源电力系统运行稳定性的功能,应用日趋广泛。但由于储能系统运行机制复杂,动态性能变化快速,因而设计储能系统监测数据在线分析方法,对于识别系统典型工况、保护设备安全运行非常关键。传统的数据离线分析方法牺牲了数据的时效性,已不能满足对储能系统实时监测的需求。在线分析实时监测数据,能更快的反馈和响应系统状态,提前预报事故发生,使系统达到长周期安全稳定运行目的,从而实现经济效益最大化。因此,储能系统典型工况的在线监控与识别成为保障系统稳定运行的关键技术与重要判据。
针对储能系统运行工况在线分析与识别的需求,文献[2]基于独立成分分析(Independent component analysis, ICA)方法提出了复合脉冲序列条件下的粒子群参数辨识方法。文献[3]针对动力储能电池,提出通过获得实时运行状态下的储能电池组功率—时间剖面图,结合ICA方法,实现储能电池工况的在线检测。文献[4]通过分析储能系统出力、输出功率等的特征参数,选出具有代表性的特征信息进行储能系统运行工况的K-means聚类分析。然而,由于储能系统实测数据动态特性变化快速,常规动态过程在线监控的分析手段ICA方法虽可有效利用高阶统计信息,在统计独立假设条件下对混合信号分离[5-8],但ICA分离算法具有数据量大、迭代次数多、收敛速度慢的问题,为此改进的FastICA方法提升了计算效率,适用于大规模监测数据的在线处理,但FastICA依然受到独立分量必须满足非高斯分布假设的局限[9]。为使信号分析不受源信号概率分布形式假设的影响,KSICA方法一旦寻找到最优解,在迭代过程将始终保持在最优解处,且在最优解处始终为正值,保持稳定性。文献[10]将KSICA方法应用于数据批处理以及移动、静止音源分离,结果显示:与FastICA方法相比,KSICA方法的数据分析性能指标偏差明显降低,且收敛速度更快,因而应用KSICA方法进行在线分析具有可行性。但将KSICA方法应用于储能系统监测数据在线分析仍处于空白,主要由于储能系统监测数据中具有大量噪声,而KSICA方法对监测数据中的噪声干扰较敏感[11-14]。如何能将KSICA方法应用于含随机干扰的储能系统运行工况在线分析,实现储能系统运行工况的快速准确识别,成为推广储能应用亟待解决的关键所在[15-19]。
考虑储能系统在线监测工作模式变化快速、数据维数高的特性,且高维数据特征空间含有的冗余和噪声特征,增加了KSICA方法的时间及空间复杂度,降低了分析处理的精度。因此,结合PCA策略,采用PCA白化方法对储能系统在线检测数据进行预处理,有效降低监控对象维数,同时消除噪声。针对储能系统监控数据的强非线性特性,构建核函数,将监控数据投影至高维特征空间,只需进行核矩阵计算,无需计算具体非线性变换,保证算法的快速性。同时,应用KSICA方法提出高维空间的线性解决方案,不仅可在非线性数据对应的高维特征空间利用简单的线性方法进行在线快速分析,并且能有效规避维数灾难问题,实现复杂数据多元特征的准确辨识。结合了PCA策略和基于核函数的KSICA方法通过对储能系统监控数据的在线分析与评估,验证了方法的快速性、有效性和鲁棒性。
1 基于核函数的PCA-KSICA在线分析方法
1.1 PCA-KSICA独立成分分析
PCA-KSICA方法的基本思想是:对储能系统典型工况在线监测数据进行线性分解,从而得到相互独立的分量。其中,独立分量需满足非高斯分布假设。假设有l个在线监测数据 x1,x2,…,xl,分别为 m 独立源分量s1,s2,...,sm的线性组合,即
式中,A为混叠系数矩阵,X=[x1,x2,…xl]T,S=[s1,s2,…,sm]T,需在混合矩阵A、独立源信号 S 未知,并在尽量少的假设条件下,寻找解混矩阵W,使得:
则 Y=[y1, y2,…, y3]为源信号 S 的估计值。对解混获得的独立源信号进行非高斯性定量评价,利用峭度作为非高斯性的评价函数。y的峭度可定义为:
对于只有高斯分布的混合变量,需要解决FastICA算法出现的发散行为,提出在峭度度量方式中将四阶累积量替换成二阶累积量E{|Y|2}2,以便避免发散行为。峭度度量方式下的一般代价函数由C(W,α)表示:
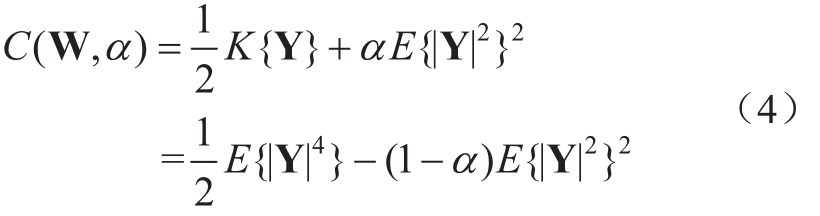
式中,α 为实值参数,α 值的改变会产生不同性质的独立成分分析算法。令 α =-1,得到新的不发散算法,定义为子带域ICA的峭度极大化(KSICA)方法。基于该方法,相应的对比函数表示为J(W)=C(W,-1)
利用牛顿法来优化KSICA方法的对比函数 J(W),其中 J(W)的梯度和海森矩阵可表示为

假定E{|Y|2XXH}≈E{|Y|2}E{XXH}, E{Y*X}E{YXH}≈E{|Y|2}E{XXH}得到
根据在点w 处的牛顿迭代法准则,KSICA滤波向量为:
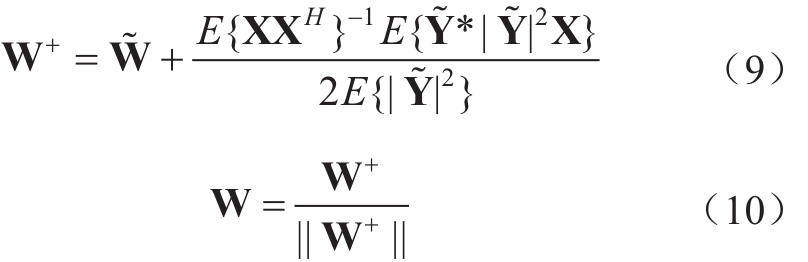
式中,W+为当前变量, =
= X。该方法在最优解处具有较强的鲁棒性。
X。该方法在最优解处具有较强的鲁棒性。
PCA-KSICA独立成分分析的步骤可以描述如下:
(1)采样储能系统正常工况下的监测数据Xnormal∈Rl×m(l 为传感器数,m为采样点数),对其均值化处理后得到Xu。
(2)根据处理后得到 Xu,应用PCA策略,求取特征值及对应的特征向量,白化后的数据Z=Λ-1/2ETX,实现降维与消噪。
(3)储能系统每次检测采样迭代时,计算优先输出信号向量 Y˜ = X W ˜ ∗ = X W i* - 1 , i = 1 , 2 , . . . 。
(4)通过计算中间变量PˆY˜,Rˆ X X和rˆXY˜,估计源信号

式中,diag{}为对角矩阵。
(5)计算临时滤波加权向量W+:
(6)更新标准化后的滤波加权向量:
(7)当满足迭代停止要求,或到达迭代步数时,使得Wopt=Wi并且停止迭代。否则回到步骤(3),将W0取成随机的单位向量。
1.2 核函数设计
储能系统具有的大量测量变量,通常是由少数独立变量所驱动。利用PCA-KSICA方法提取出这些独立变量,可以更好地反映储能系统运行过程的动态变化特征。为了快速、准确地从测量变量中分离出工况的变化,实现非线性数据向高维特征空间的映射,需设计合适的核函数,使得PCA-KSICA方法在保持鲁棒性的同时,具有快速性。
选择核函数K(x, y),将白化数据Zn映射至高维空间,在高维空间中利用KSICA得到解混矩阵W,从而估算出独立源信号Sn,即有
式中,Sn∈Rl×m为正常工况下的独立分量矩阵,An∈Rl×m为正常工况下的混合矩阵。
得到矩阵Sn之后,构造正常工况下的特征子空间Θ。即
式中, s1,s2,…sm分别为经KSICA分离后得到的各独立分量。将经PCA白化后待监测信号Zp投影至特征子空间Θ,设待辨识信号Zp∈Rl×m,即有
式中,矩阵Ap∈Rl×m为各测量信号在特征子空间Θ的投影系数矩阵,可求得:
式中,Sn+为矩阵 Zp 的Moore-Penrose广义逆。当储能系统出现异常情况时,与 An 相比,投影系数矩阵 Ap 将会有较大的特征改变,因此在特征空间设计适当的分类器,可以进一步实现储能系统不同工况识别。定义性能指标:
式中,Adiff =Ap-An,σmax()为矩阵的最大奇异值。从(20)式可知,当储能系统处于正常工况时,指标 I 值较小;相反,指标 I 值将变大。实时监控系统运行,处于不同工况的性能指标值会有明显的分布差异,根据投影系数矩阵 Ap可进行典型工况识别。
2 储能系统典型工况在线分析实例
以上海市某投入运行的风电平滑储能系统为例,选取该储能系统四月某日并网点功率、储能功率、1 min波动率作为样本数据,如图1所示。该数据为 1 min采样,将该天储能系统的测量数据作为浅充浅放的样本数据,并对其进行PCA-KSICA算法分析,得到各独立分量。利用得到的各独立分量构造如图2所示的特征子空间,并利用混合矩阵 An 作为后续的性能评价。
选取深充深放和浅充浅放为储能系统两类典型运行工况,当可再生能源独立运行、储能作为主电源承担负荷转移功能时,储能系统常工作在深充深放状态;当可再生能源并网运行、储能系统承担平滑并网功率与提升并网电能质量功能时,储能系统常工作在浅充浅放状态。进行储能系统典型工况在线实时分析时,采用滑动窗口技术逐步更新在线检测的数据矩阵,将滑动窗口长度选取为60 min,将其投影到浅充浅放下的特征子空间,并按式(20)实时计算当前指标值I。根据当前监控指标值和分布值来判定储能系统目前是否处于浅充浅放工作状态。
取四月另一日储能系统处于深充深放状态的并网点功率、储能系统功率、1 min波动率作为测试数据投影至特征子空间,如图3所示,观察性能指标变化,验证利用基于核函数的PCA-KSICA方法进行储能系统典型工况在线识别的有效性。
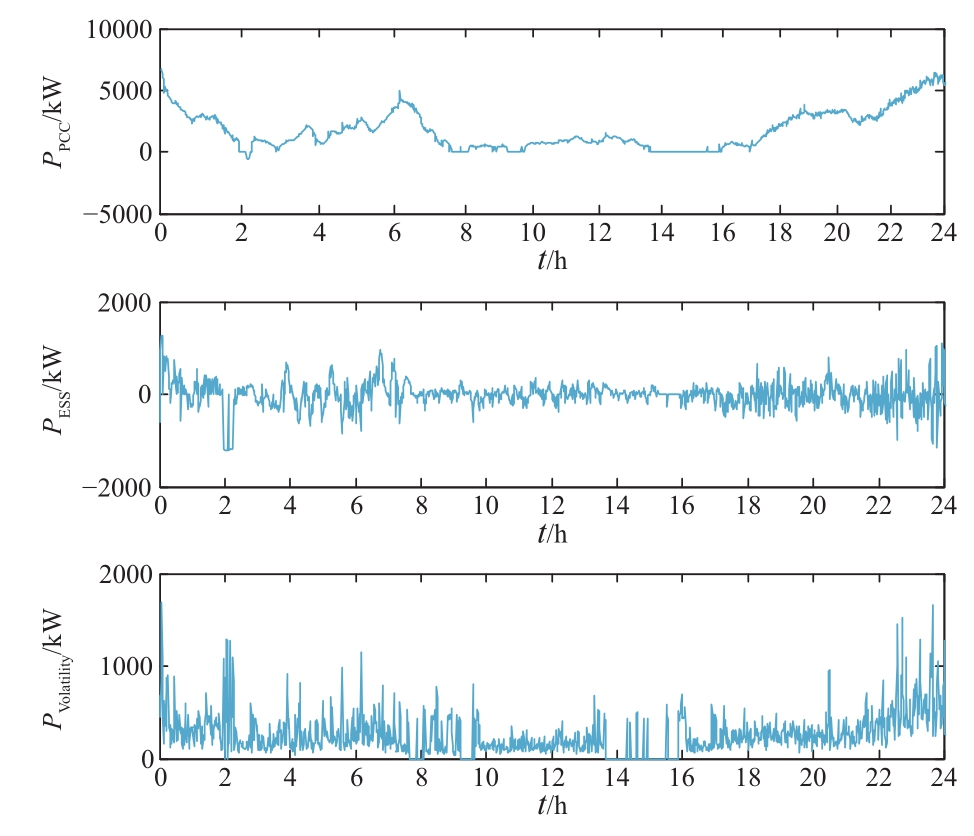
图1 PCC点及储能信号波形图(浅充浅放)
Fig. 1 PCC point and energy storage waveform (low depth charge and low depth discharge)
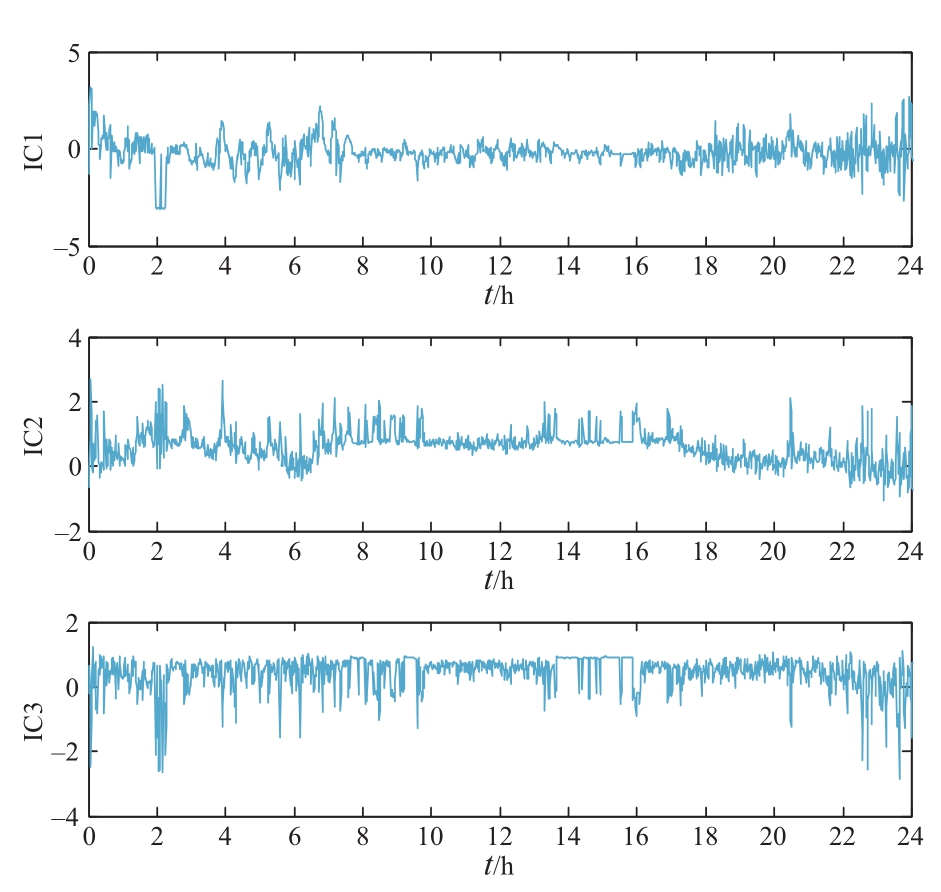
图2 独立分量波形图(浅充浅放)
Fig. 2 Independent component waveform (low depth charge and low depth discharge)
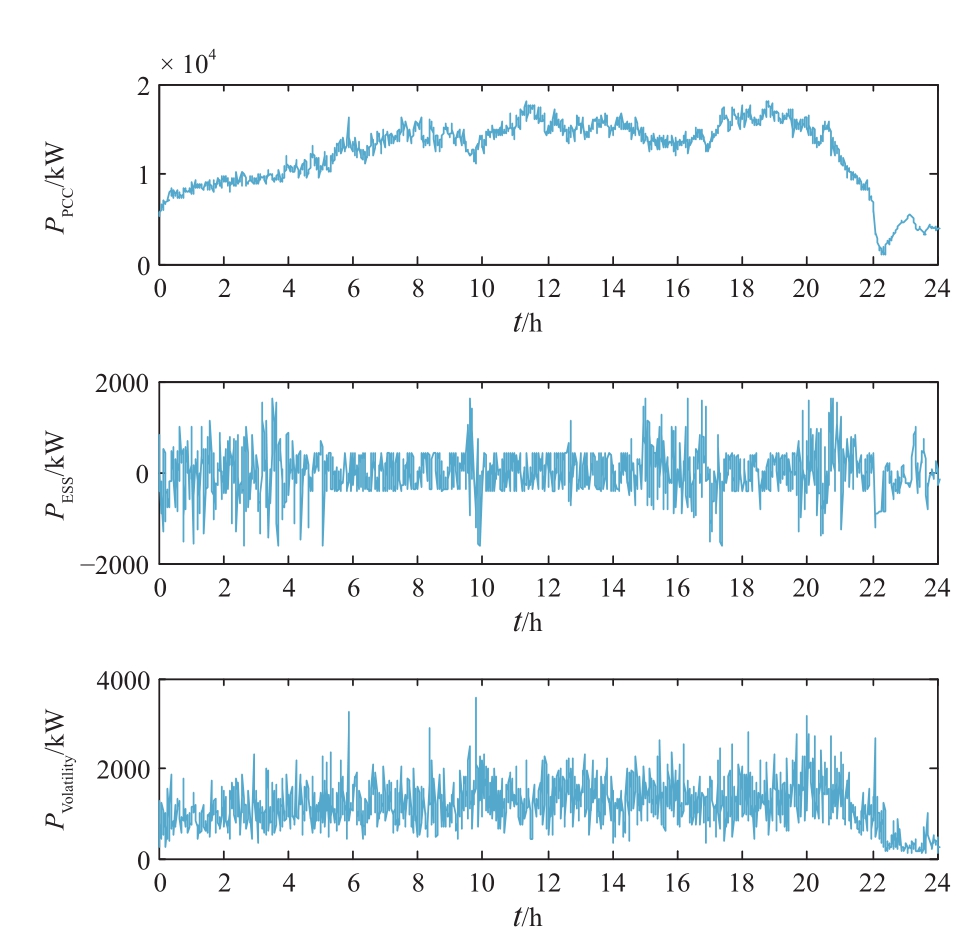
图3 PCC点及储能信号波形图(深充深放)
Fig. 3 PCC point and energy storage waveform (deep charge and deep discharge)
图4 、图5分别为浅充浅放工况下性能指标值I与性能指标分布图,由性能指标分布图可看出,浅充浅放阶典型工况的性能指标值集中于1.4~2.8之间,性能指标值分布范围为0~7。图6、图7分别为深充深放工况下性能指标值I与性能指标分布图,由性能指标分布图可以看出,深充深放典型工况的性能指标值集中于1.9~3.4之间,性能指标值分布范围为1~9。根据性能指标值I的集中分布情况,结合现场实测数据分析,当储能系统性能指标值集中于0~2.4时,判定为浅充浅放工况;当储能系统性能指标值集中于2.4~5时,判定为深充深放工况。
由图1~图7分析可知:在构建特征子空间并将图3所示的PCC点及储能功率信号数据矩阵Zn投影至特征子空间中时,KSICA方法采用批处理的方式,在定点处进行寻优迭代,使得数据收敛更加快速、稳健。同时由于PCC点及储能功率信号在对应的高维特征空间可以利用简单的线性方法进行分析,进一步提高了在线分析的快速性。比较性能指标值与性能指标分布图,可以有效辨识储能系统不同运行工况的差异。因此,基于核函数的PCA-KSICA方法可以快速识别储能系统的典型工况,实现储能系统不同工况的准确在线分析。
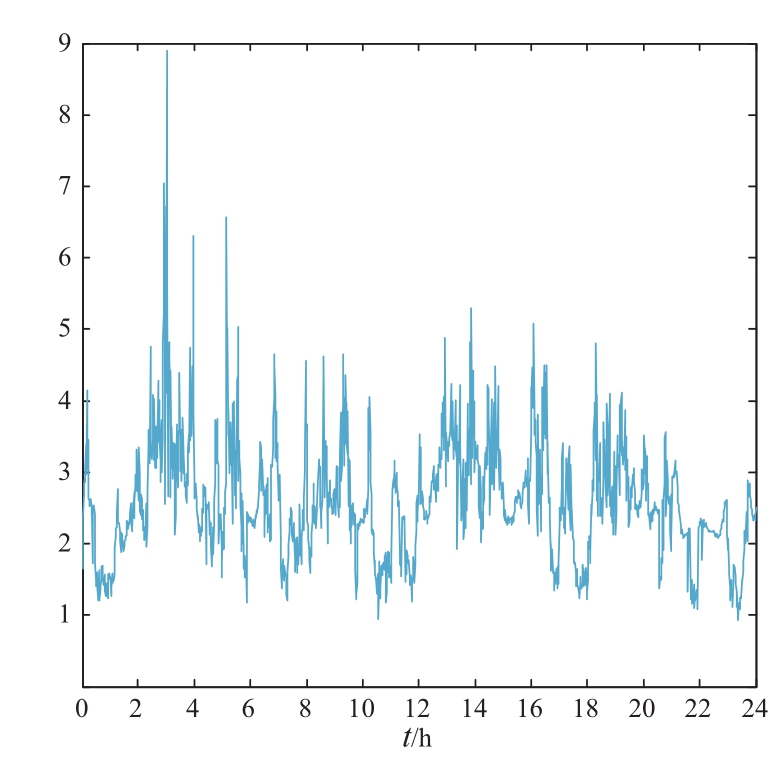
图4 指标I波形图(浅充浅放)
Fig. 4 Index I (low depth charge and low depth discharge)

图5 指标I分布图(浅充浅放)
Fig. 5 Index I distribution (low depth charge and low depth discharge)
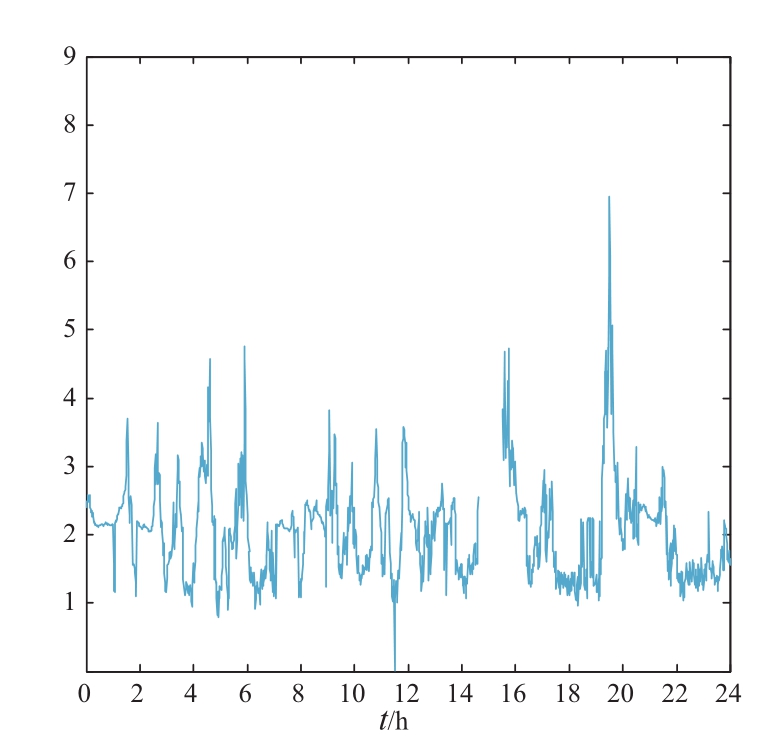
图6 指标I波形图(深充深放)
Fig. 6 Index I (deep charge and deep discharge)

图7 指标I分布图(深充深放)
Fig. 7 Index I distribution (deep charge and deep discharge)
3 结束语
针对储能系统动态过程在线监测数据的动态快速变化、高阶、强非线性特性,提出基于核函数的储能系统典型工况PCA-KSICA识别方法。通过白化实现降维与消噪,同时将非线性数据映射至高维核空间,在高维线性空间中利用KSICA分离独立分量。将储能系统工作过程看作由独立变量实现驱动,通过采用所提出的基于核函数的PCA-KSICA在线分析方法,可以实现在消除高维变量之间相关性的同时,大大减少数据的维数,消除随机噪声影响。构造浅充浅放工况下的特征子空间,利用滑动窗口技术,将待辨识的数据矩阵投影至该空间,并设计适当的性能指标表征实时工况。将所提出的方法应用于储能系统工况识别的在线分析,结果表明该方法能够准确、快速获得有效的性能指标值,并对典型工况进行区分与评估。
参考文献
[1] 丛晶,宋坤,鲁海威,等.新能源电力系统中的储能技术研究综述[J].电工电能新技术,2014,03:53-59.
Cong Jing, Song Kun, Lu Haiwei, et al. Review of Energy Storage Technology for New Energy Power System[J].Advanced Technology of Electrical Engineering and Energy,2014, 03: 53-59(in Chinese).
[2] 张言茹,姜久春,张维戈,等.储能工况下磷酸铁锂电池动态辨识方案研究[J].电源技术,2014,38(11):2037-2041.
Zhang Yanru, Jiang Jiuchun, Zhang Weige, et al.Dynamic Parameter Identification Method of Lithium Iron Phosphate Cell for BESS[J]. Chinese Journal of Power Sources, 2014,38(11): 2037-2041(in Chinese).
[3] 孙逢春,孟祥峰,林程,等.电动汽车动力电池动态测试工况研究[J].北京理工大学学报,2010,30(3):297-301.
Sun Fengchun, Meng Xiangfeng, Lin Cheng, et al. Dynamic Stress Test Profile of Power Battery for Electric Vehicle[J].Transactions of Beijing Institute of Technology, 2010,30(3):297-301(in Chinese).
[4] 陈继忠,胡娟,武国良,等.模块化储能系统工况测试方法[J].电网技术,2016,40(11):3482-3488.
Chen Jizhong, Hu Juan, Wu Guoliang, et al.Research of Duty Cycle Test Method for Module ESS[J].Power System Technology, 2016, 40(11):3482-3488(in Chinese).
[5] F. Karimzadeh, S. Esmaeili, S. Hossein Hosseinian. Method for determining utility and consumer harmonic contributions based on complex independent component analysis[J]. IET Generation, Transmission & Distribution. 2016, 10(2): 526-534.
[6] L. Cheng, B. Gao, G. Y. Tian, et al. Impact Damage Detection and Identification Using Eddy Current Pulsed Thermography Through Integration of PCA and ICA[J]. IEEE Sensors Journal, 2014, 14(5): 1655-1663.
[7] M. Hui, R. Li, K. Chen, et al. Long Improved Estimation of the Number of Independent Components for Functional Magnetic Resonance Data by a Whitening Filter[J]. IEEE Journal of Biomedical and Health Informatics, 2013, 17(3): 629-641.
[8] J. Ji. Robust Approach to Independent Component Analysis for SAR Image Analysis[J]. IET Image Processing, 2012, 6(3):284-291.
[9] B. Sallberg, N. Grbic, I. Claesson. Complex-valued Independent Component Analysis for Online Blind Speech Extraction[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2008, 16(8): 1624-1632.
[10] Benny Sällberg, Nedelko Grbic, Ingvar Claesson. Complex-Valued Independent Component Analysis for Online Blind Speech Extraction[J]. IEEE Transactions on Audio, Speech,and Language Processing, 2008, 16(8): 1624-1632.
[11] 王建雄,张立民,钟兆根.基于FastICA算法的盲源分离[J].计算机技术与发展,2011,12:93-96.
Wang Jianxiong, Zhang Limin, Zhong Zhaogen. Blind Source Separation Based on FastICA Algorithm[J]. Computer Technology and Development, 2011, 12: 93-96(in Chinese).
[12] 杜宇慧,桂志国,刘迎军,等.基于独立成分分析的脑功能网络分析方法综述[J].生物物理学报,2013,04:266-275.
Du Yuhui, Gui Zhiguo, Liu Yingjun, et al. Review of Independent Component Analysis Methods for Brain.functional Networks[J].Acta Biophysica Sinica, 2013, 04: 266-275(in Chinese).
[13] 彭中亚,程国建.基于独立成分分析和核向量机的人脸识别[J].计算机工程,2010,07:193-194.Peng Zhongya, Cheng Guojian.Face Recognition Based on Independent Component Analysis and Core Vector Machines[J]. Computer Engineering, 2010, 07: 193-194(in Chinese).
[14] G. S. Fu, R. Phlypo, M. Anderson, et al. Complex Independent Component Analysis Using Three Types of Diversity: Nongaussianity, Nonwhiteness, and Noncircularity[J]. IEEE Transactions on Signal Processing, 2015, 63(3): 794-805.
[15] F. Nesta, P. Svaizer, M. Omologo. Convolutive BSS of Short Mixtures by Ica Recursively Regularized Across Frequencies[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 19(3): 624-639.
[16] H. Shen, S. Jegelka, A. Gretton. Fast Kernel-based Independent Component Analysis[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3498-3511.
[17] A. Hyvarinen. Gaussian Moments for Noisy Independent Component Analysis[J]. IEEE Signal Processing Letters, 2002,6(6): 145-147.
[18] 董玉亮,李亚琼,曹海斌,等.基于运行工况辨识的风电机组健康状态实时评价方法[J].中国电机工程学报,2013,11:88-95+15.
Dong Yuliang, Li Yaqiong, Cao Haibin, et al. Real-time Health Condition Evaluation on Wind Turbines Based on Operational Condition Recognition[J]. Proceedings of the CSEE, 2013, 11:88-95+15(in Chinese).
[19] 梁胜杰,张志华,崔立林,等.基于主成分分析与核独立成分分析的降维方法[J].系统工程与电子技术,2011,09:2144-2148.
Liang Shengjie, Zhang Zhihua, Cui Lilin, et al. Dimensionality Reduction Method Based on PCA and KICA[J]. Systems Engineering and Electronics, 2011, 09: 2144-2148(in Chinese).
PCA-KSICA Online Analysis Method of Energy Storage System Typical Operating Conditions Based on Kernel Function
LIU Shu 1, WANG Yu-fei2, ZHANG Yu 1, XUE Hua2, HU Ying-jun2
(1. State Grid Shanghai Electric Power Research Institute, Hongkou District, Shanghai 200437, China;2. School of Electrical Engineering, Shanghai University of Electric Power, Yangpu District, Shanghai 200090, China)
Abstract: This paper proposes a PCA-KSICA online analysis method of energy storage system typical operating conditions based on kernel function. By combining the PCA with the KSICA, the two order correlation between the original data is eliminated by PCA whitening process, and by building kernel function, the slow convergence speed of the ICA algorithm is effectively solved. KSICA is a theoretical analysis of a certain criterion for complex-valued independent component analysis(ICA) with a focus on blind speech extraction (BSE) of a spatio-temporally nonstationary speech source. The proposed method is shown to share the important fixed-point feature with the FastICA method, although an improvement with the proposed method is that it does not exhibit the divergent behavior for a mixture of Gaussian-only sources that the FastICA method tends to do, and it shows robust performance in online implementations. It is used in the feature extraction of the energy storage system, the results verify the effectiveness and feasibility of the proposed method.
Keywords: PCA-KSICA method; kernel function; energy storage system; typical operating conditions online analysis
Project Supported by Science and Technology Foundation of SGCC(DG71-14-046).
作者简介:

刘舒
刘舒(1987),女,硕士,主要从事微网、储能、新能源并网等方向研究工作。E-Mail:liushu@sh.sgcc.com.cn。
王育飞(1974),男,博士,副教授,研究方向为电力储能应用技术、电能质量分析与控制等。
张宇(1970),男,高级工程师,研究方向为智能配电。E-mail:zhangyu@sh.sgcc.com.cn。
(责任编辑 张鹏)
