0 引言
锂离子电池的健康状态(state of health, SOH)可表征锂离子电池的老化衰退程度,但不同的研究机构或文献对锂离子电池的健康状态的定义和研究方法各不相同[1]。文献[2]通过对等效电路模型和容量模型状态空间方程的时间尺度变换,得到可用于电池荷电状态(state of charge, SOC)和容量联合估计的系统模型,并采用多尺度扩展卡尔曼滤波算法(MEKF)估计电池容量,进而得到SOH。文献[3]利用容量增量分析和差分电压分析等原位电化学分析方法对电池开路电压特性变化进行分析,建立电池容量衰退与其衰退机理的量化关系,建立基于电池开路电压曲线的容量估计模型用于电池健康状态估计。文献[4]在锂离子电池多物理参数模型的基础上,对参数辨识及内部健康特征提取方法进行了深入研究,挖掘内部健康特征随电池老化过程的变化规律,并依此对造成电池循环性能下降的因素进行了定量分析,最终获得了丰富的电池内部健康状态信息。此外,还有基于模型[5]、内阻[6]、循环次数或其他参数[7]的电池健康状态评估方法。
电池的健康状态最常见的定义为基于电池最大可用容量,即锂离子电池当前最大可用容量与出厂时的额定容量之比,因此电池健康状态问题通常转化为容量估计问题[8]。本文以电池容量增量曲线(IC曲线)为分析工具,提出以电池实际容量定义为主,IC曲线特征变化为辅的电池健康状态诊断方法。电池容量增量曲线随电池老化衰退的变化反映了电池动力学与热力学特性的改变,因此基于电池IC曲线的变化规律可近似判断单体电池的衰退机理,有助于分析电池的衰退老化原因,同时可以预测电池的衰退轨迹,对电池的安全性及使用方法做出指导。以电池容量增量曲线为工具的电池健康状态诊断方法,估计容量的误差可控制在2%以内,取得了较好的效果。
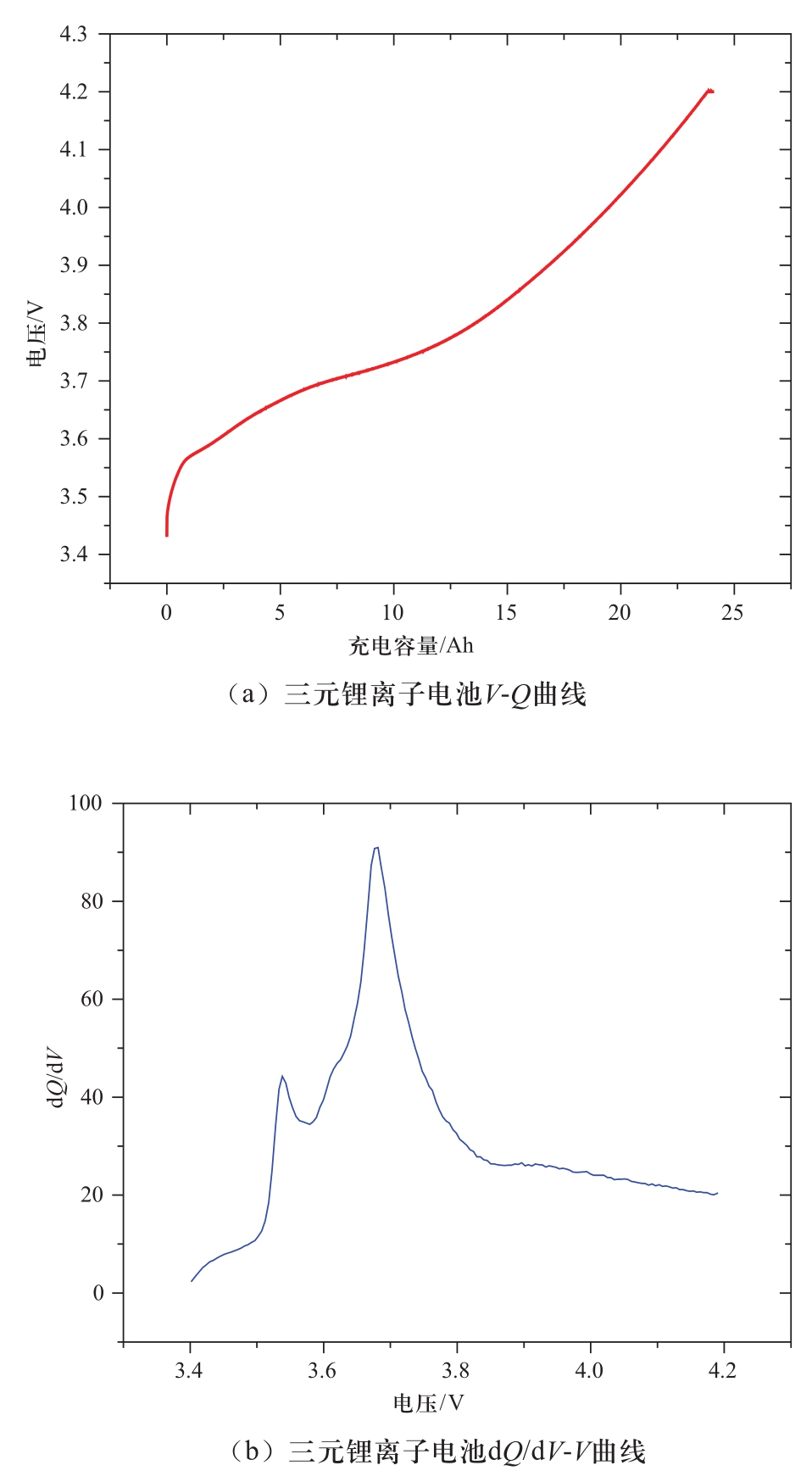
图1 三元锂离子电池电压曲线和容量增量曲线
Fig. 1 The terminal voltage as a function of charged capacity and IC curves for NCM battery
1 电池容量增量曲线
容量增量分析法是分析电池衰退机理的重要分析方法,其核心为电池容量增量曲线(IC曲线)[9]。本研究主要以一支国内某厂商生产的25 Ah三元锂离子电池为对象,其充电电压曲线如图1(a)所示,横轴为充电容量,纵轴为电池端电压。由图1(a)可以看出,在电池充电的初期和末期,电压上升迅速;而在充电曲线中部,电压上升缓慢。事实上,电压上升缓慢的平台部分充入了绝大部分容量。电池容量增量分析法是将原始的充电数据经过处理,求出dQ/dV数据(充电容量对电池端电压求导),继而得到dQ/dV-V曲线(IC曲线),如图1(b)所示,其优点是将电压曲线上电压上升缓慢,而电池内部反应剧烈的电压平台区转化成容量增量曲线上易于观察和分析的dQ/dV峰,进而使在电压曲线上不易被发现的微小变化可以在IC曲线上反映出来。具体以三元锂离子电池为例,在整个充电过程中,正极的反应过程主要为镍离子(Ni+)由二价离子(Ni2+)转化为三价离子(Ni3+),和三价离子(Ni3+)转化为四价离子(Ni4+)这两个反应;而负极反应过程为石墨(碳)的5个状态(C6、C72、C36、C18、C12)之间的4次相变。图1(a)中多个电压平台的出现是电池正负极不同反应相互叠加的结果,而图1(b)中每个IC峰分别对应了图1(a)中不同的电压平台[10]。同时,对于电池循环老化过程中不同老化程度的IC曲线特征的分析,如IC峰的高度、左右位置、峰包含的面积等参数,可以分析判断电池老化衰退的模式和机理,进而对电池的健康状态进行诊断。
2 电池健康状态表征参数及变化特性
2.1 容量增量曲线中的特征参数
使用电池容量估计模型估计电池的实际容量,第一步是要选择和甄别模型的自变量。锂离子电池的容量增量曲线由若干个IC峰构成,因此在容量增量曲线中,易于提取的特征参数包括各峰的位置(峰值处对应的横轴电压值)、各峰的高度、各峰包含的面积及各峰左右侧斜率。三元锂离子电池容量增量曲线中各参数示意如图2所示,初步选择的特征参数包括I峰高度、I峰包含的面积、I峰左右侧斜率、I峰位置、II峰高度、II峰包含的面积、II峰左右侧斜率、II峰位置及III峰包含的面积共11个参数。
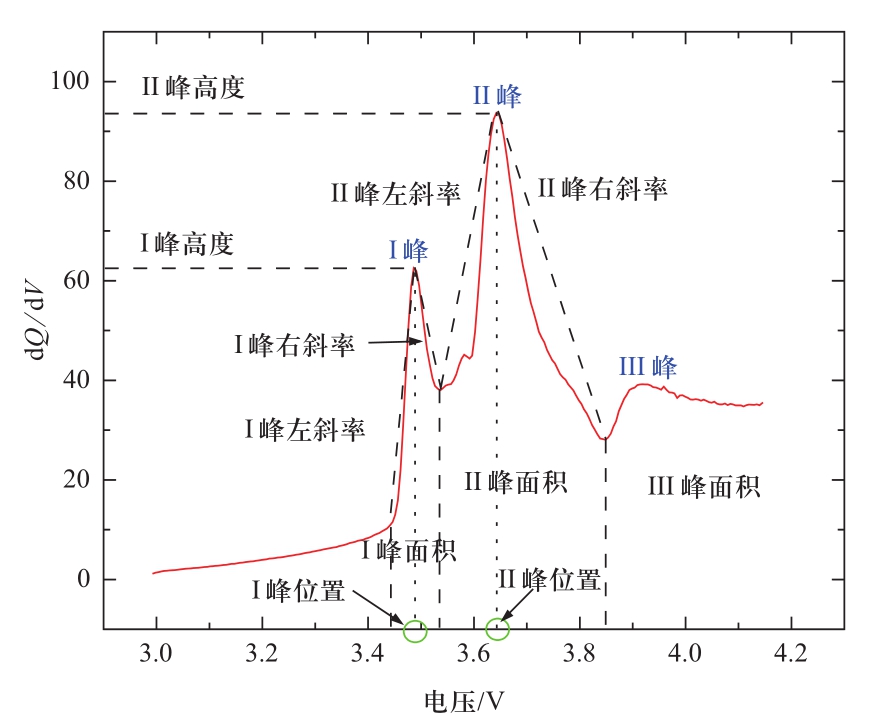
图2 三元锂离子电池IC曲线中的特征参数示意图
Fig. 2 The diagrammatic sketch of IC curve characteristic parameters for a NCM battery
初步提取的11个参数全部用于模型训练过于冗余,且数据预处理的任务量巨大,若多个自变量之间存在较强的线性关系,则回归过程中会出现多重共线性问题,因此需对特征参数进行简化[11]。
首先,从实际应用中数据源获取方面,在电动汽车实车电池组和储能电池组中,通常会出现单体电池不一致性问题,包括容量、内阻、SOC等不一致性。由于电池组内各单体SOC不一致性的存在,绝大多数电池无法满充满放。因此,若将图2中与SOC最高点或最低点有关的参数纳入自变量,如I峰包含的面积、III峰包含的面积等,则可能出现模组中的单体电池因无法全充全放而不能获得参数数据的情况,因此剔除依赖电池满SOC运行的I峰包含的面积、III峰包含的面积及I峰左侧斜率。在特征量之间的数学关系方面,I峰右侧斜率与II峰左侧斜率完全由两峰高度与两峰之间的极小值点决定,在两峰高度已经被选定为两个特征参数的前提下,I峰右侧斜率与II峰左侧斜率取决于两峰之间极小值的数值及左右侧位置,且两者呈负相关关系,因此二者可选其一;由于锂离子电池IC曲线的主峰(II峰)更能反映电池热力学特性,II峰斜率体现了电池进入相变的快慢,因此选择保留II峰左侧斜率;此外,从图2和IC曲线数据可以看出,I峰位置与II峰位置的偏移量几乎完全相同,这是由于电池内阻和极化随老化的增加在全SOC中几乎相同,因此剔除I峰位置而保留II峰位置。综上所述,剔除I峰包含的面积、III峰包含的面积、I峰左侧斜率、I峰右侧斜率及I峰位置这5个特征参数,剩余6个特征参数,分别为I峰高度、II峰高度、II峰面积、II峰位置、II峰左斜率、II峰右斜率。
2.2 电池老化衰退模式的识别
三元锂离子电池的老化一般分为热力学特性的衰退和动力学特性的衰退,不同老化模式反映在容量增量曲线(IC曲线)中的变化是不同的。热力学损失通常使用小电流(如0.05C)充放电数据绘制的IC曲线来研究,电池热力学损失可以分为锂离子的损失和正负极活性材料的损失:锂离子的损失通常会导致III峰面积的减小,而负极材料的损失通常会导致I峰和II峰面积的减小。动力学损失通常使用大电流(如1C)充放电数据绘制的IC曲线来研究,电池动力学特性的老化主要体现为锂离子电池阻抗的增加,在容量增量曲线上体现为曲线整体的偏移。对于充电过程的容量增量曲线,若阻抗增加,则曲线向右侧(高电压方向)移动。
本文实验方案为1C恒流恒压充放电循环。电池共进行600次充放电循环,容量衰退了约1.34 Ah(5.28%)。不同循环次数的IC曲线如图3所示,可以看出,与图2中的IC曲线相比,图3中的IC曲线几乎观察不到III峰,这是由于充放电电流较大,其IC曲线不能很好地体现各相变过程。从0次循环到600次循环,在热力学特性方面,依据小电流IC曲线分析方法,由于II峰高度和面积下降明显,因此负极活性材料损失明显,但由于不能观察到反映锂离子损失的III峰,因此锂离子的损失不能确定;在动力学特性方面,曲线整体向右偏移明显,说明电池动力学老化严重,电池内阻明显增大[12]。
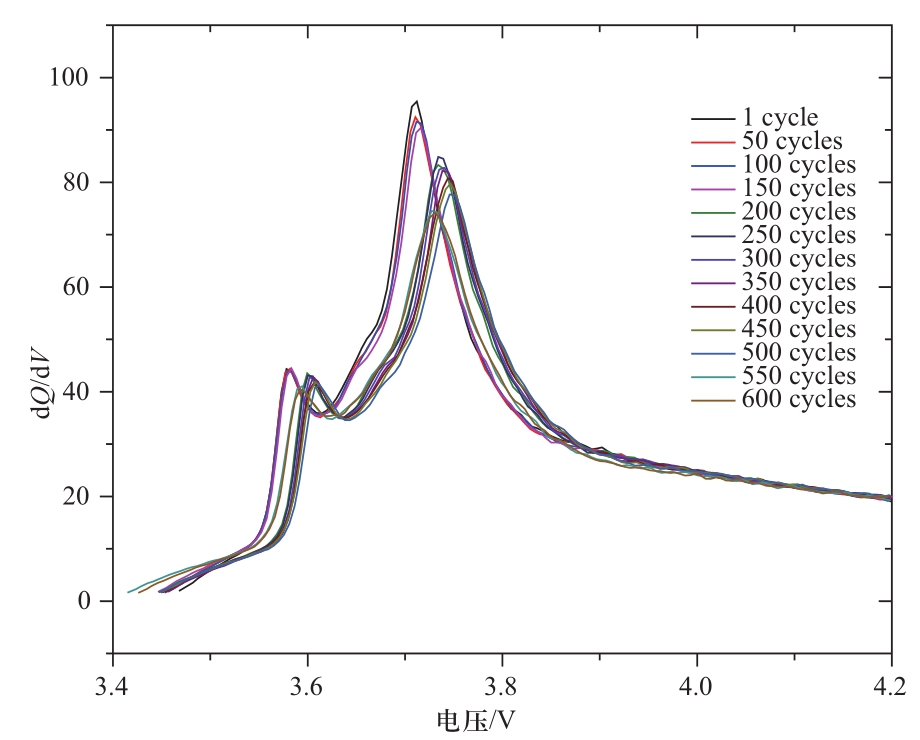
图3 三元锂离子电池IC曲线随老化的变化过程
Fig. 3 IC curves evolutions as the NCM battery degradation
2.3 参数相关性分析
随着电池循环次数的增加,电池老化衰退加剧,图3中IC曲线中的参数也随之发生变化,但各参数变化情况不同,某些参数变化较大且规律明显,某些参数变化不明显或不规律。因此要从多个参数中,筛选出与电池老化衰退紧密相关的参数。反映电池老化衰退程度最直接的特征是电池最大可用容量的减少,因此探究各参数与电池最大可用容量的相关性,即可得出参数与电池老化衰退关系是否密切。各参数与电池最大可用容量之间的关系如图4所示。
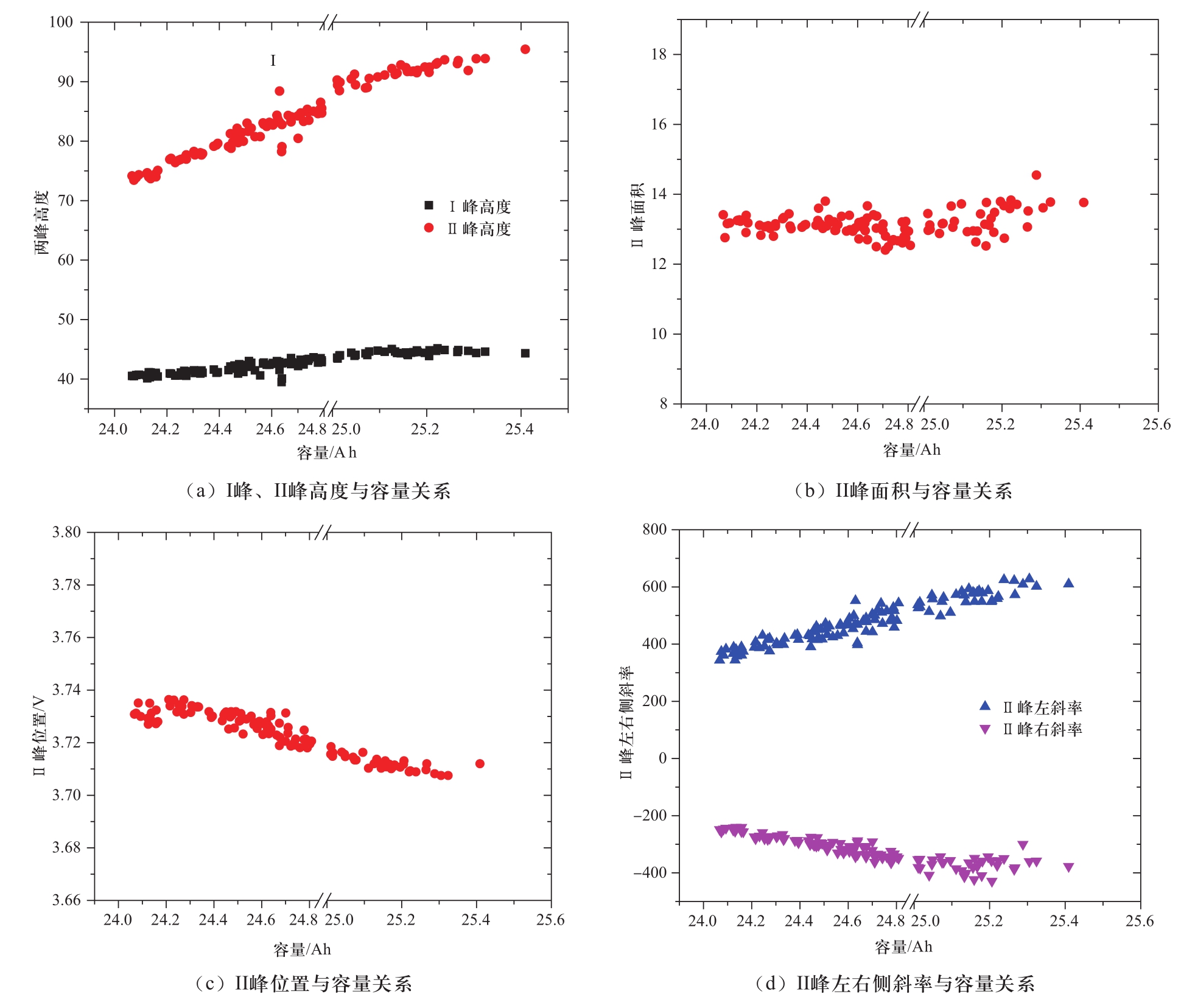
图4 25 Ah三元锂离子电池IC曲线中各参数与容量关系
Fig. 4 The relationships between the parameters of IC curves lithium-ion battery and the available capacity
由图4可知,6个参数中,峰面积与容量之间无明显相关性,其余参数与容量之间均有一定的线性关系。进一步定量分析各参数与最大可用容量,以及各参数之间的相关性,判断特征参数之间是否存在多重共线性问题[13]。
皮尔逊相关系数[14]作为衡量两个量之间相关性大小的重要指标,受到广泛应用。皮尔逊相关性系数的计算公式为
式中,X和Y为两个变量,COV(X,Y)为变量X和Y的协方差,σX、σY 分别为变量X和Y的标准差。皮尔逊相关系数的值介于-1和1之间:若大于0,说明两个变量呈正相关关系;若小于0,说明两个变量呈负相关关系;若相关系数为0,则两个变量无关系。两个变量之间的皮尔逊相关系数的绝对值越大,从一个变量去预测另一个变量的精确度就越高,这是因为相关系数越高,从其中一个变量的变化就可越多地获知另一个变量的变化。分别计算从三元锂离子电池IC曲线中提取的7个变量与最大可用容量的皮尔逊相关性系数,结果如表1所示。
表1 特征参数与最大可用容量的皮尔逊相关系数
Table 1 The pearson correlation coefficient between characteristic parameters and available capacity

表1的结果显示,多个变量与电池最大可用容量之间均存在较强的相关性。进一步分析各特征参数之间的相关性,分析6个选定变量之间的相关性,各变量之间的皮尔逊相关系数如表2所示。
表2 6个特征参数之间的皮尔逊相关系数
Table 2 The pearson correlation coefficient between six characteristic parameters
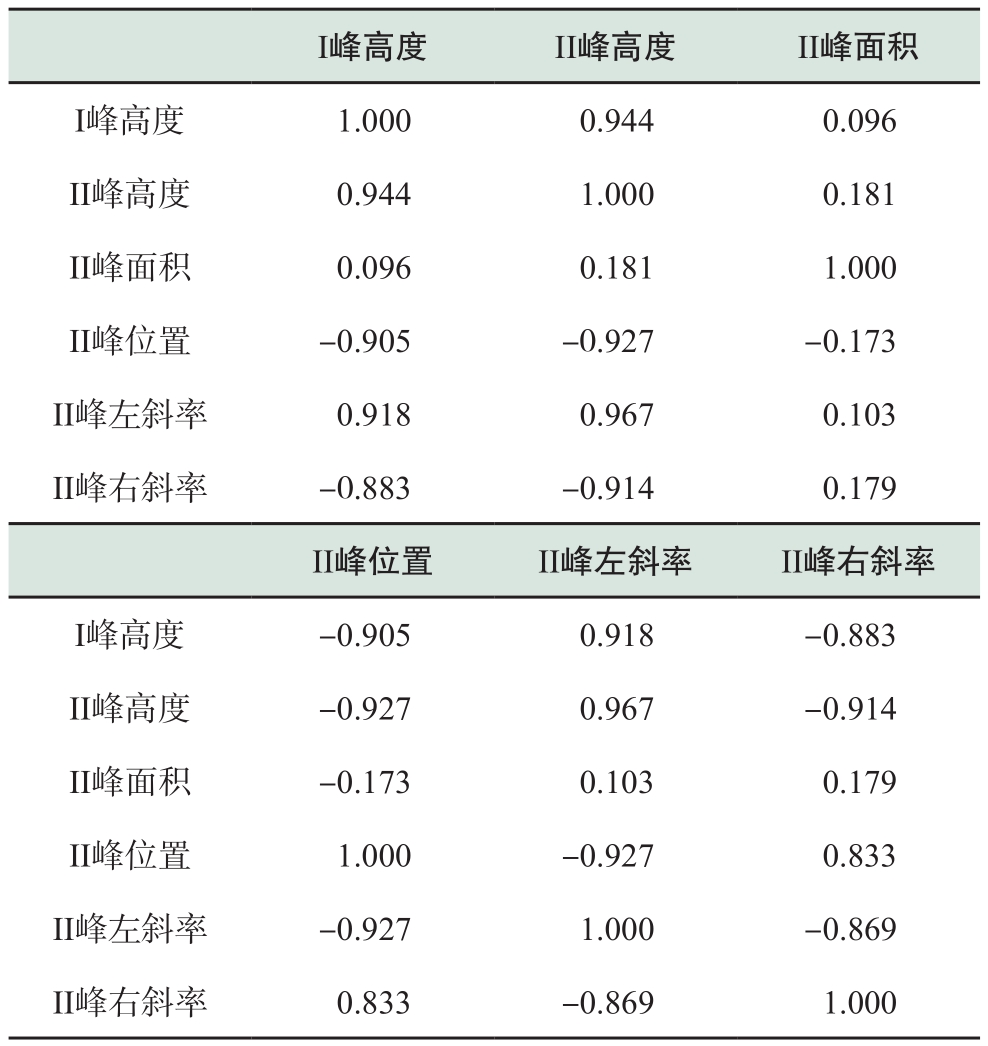
表2显示多个变量之间存在较强的相关性,如I峰高度与II峰高度之间的相关系数达到了0.944,II峰右斜率与II峰高度之间的相关度达到了-0.914,说明两个参数之间的相关度非常大。在线性回归中,相关度较高的参数一同作为自变量会引起多重共线性(Multicollinearity)问题。多重共线性是指线性回归模型中的解释变量之间由于存在高度的相关关系而使模型估计失真或难以估计准确,其危害在于,在增大无用计算量的同时,使得回归方程变得不稳定,变量的系数对样本的抽取过于敏感;某些回归系数的符号与实际意义相反,难以区分每个解释变量对因变量的单独影响;有些重要自变量的显著性被隐藏起来,回归方程和回归系数通不过显著性检验等。方差膨胀因子(VIF)可定量表征共线性严重程度,其计算公式为
式中,R2表示以此自变量为因变量时,对其他自变量回归的复测定系数。
经验判断方法表明:当0<VIF<10,不存在多重共线性;当10≤VIF<100,存在较强的多重共线性;当VIF≥100,存在严重多重共线性。计算各特征参数的VIF值,结果如表3所示。
表3 特征参数的方差膨胀因子(VIF)值
Table 3 The VIF of characteristic parameters
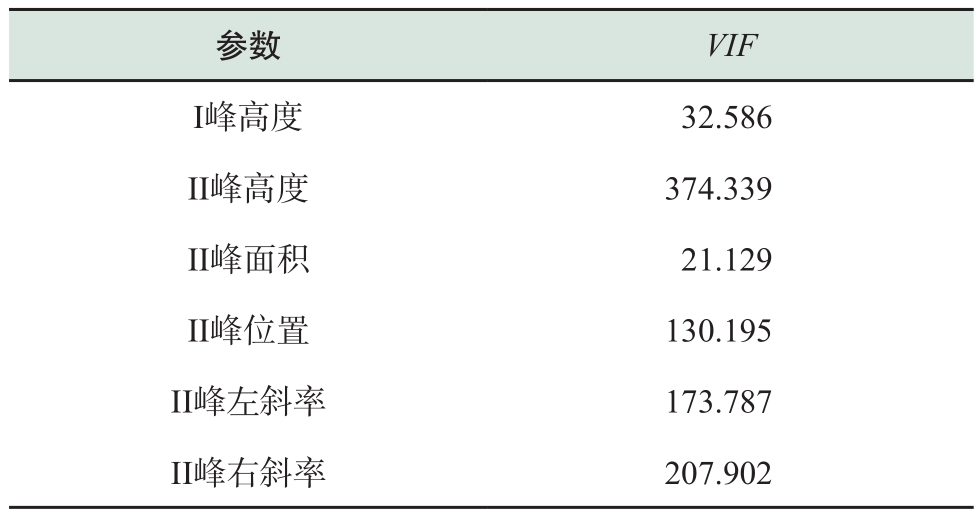
VIF结果显示,多个特征参数的VIF大于100,最大值约为375,因此变量之间存在较严重的共线性,不能直接使用简单的多元线性回归直接估计。在此,选择使用可以针对解决多重共线性的回归方法—主成分回归,建立三元锂离子电池容量估计模型,并将回归估计结果与最常用的多元线性回归的结果做比较,证明方法的优劣性。
3 基于主成分回归(PCR)的三元锂离子电池容量估计方法
3.1 主成分回归的原理
主成分回归(PCR)是一种典型的解决多重共线性问题的回归方法,其包括主成分分析(PCA)和回归分析两部分。主成分分析法是一种典型的降维统计方法,其基本原理是将原有的多个相关性较强的变量x1,x2……xP重新组合,生成少数几个彼此不相关的变量F1,F2……FN,使它们尽可能多地反映原有变量的信息,其中转换后的F1,F2……FN就叫作主成分,分别称为第一主成分、第二主成分……第N主成分。其在几何上表现为将原非正交的坐标系变换成新的正交坐标系,使之指向样本点最分散的N个正交方向。主成分回归中的回归部分即为普通的最小二乘回归,其自变量为主成分分析后得到的N个主成分,因变量为标准化后的原因变量。由于主成分分析后得到的主成分为正交关系,因此不会存在多重共线性问题。
主成分回归的主要步骤如图5所示[15],其中步骤(a)中的数据标准化方法如公式(3)所示
式中,x为原变量,u为变量数据的均值,σ为变量数据的标准差。

图5 主成分回归步骤
Fig. 5 The procedure of the principal components regression
3.2 基于主成分回归的容量估计模型的实现
具体到实验数据,先对6个参数进行主成分分析(PCA)。KMO值是表征数据是否适用于主成分分析的参数,介于0~1之间,其值越接近1说明变量间的相关性越强,数据越适用于主成分分析。三元锂离子电池IC曲线特征参数数据的KMO值为0.716,说明PCA较适用于此数据的降维处理。降维结果显示,两个主成分的方差大于1,且两个主成分的累积方差百分比达到95.025%,说明两个主成分包含了原6个变量95.025%的信息,因此认定此两个主成分为主成分分析的降维结果,分别命名为ZF1、ZF2,得到ZF1和ZF2的表达式为
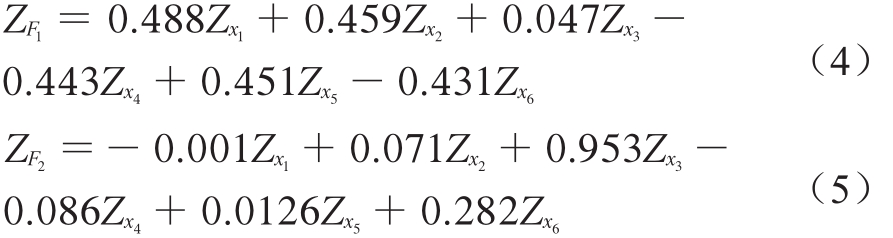
式中,Zx1~Zx6分别表示6个特征参数标准化后的数据,数据标准化方法如公式(3)所示。
依据公式(4)、(5)计算得出主成分变量ZF1和ZF2的数据。将ZF1和ZF2作为自变量,标准化后的容量ZQ作为因变量,使用最小二乘法建立回归模型,得出ZF1、 与容量ZQ的关系为
与容量ZQ的关系为
将公式(4)、(5)代入式(6),得到标准化的容量与标准化的6个自变量的关系为
将公式(7)中所有变量依据公式(3)还原到非标准化的原始变量,得到最终的容量估计模型公式为
式中,x1~x6分别表示三元锂离子电池容量增量曲线(IC曲线)中的I峰高度、II峰高度、II峰面积、II峰位置、II峰左斜率、II峰右斜率。
使用原数据检验回归模型的准确性,误差如图6所示。误差结果显示,绝大多数循环误差均控制在0.2 Ah(1%)以内,考虑到测量误差和测量过程中可能出现的离群坏点,模型误差稳定控制在2%以内,说明容量估计准确度较高。同时,式(8)各参数的系数正负号与表1中的容量和各特征参数的相关性完全相符,说明结果解释性较好,不存在多重共线性问题。依据本文中基于电池容量的健康状态定义,模型估计得到的电池实际容量与电池出厂时的额定容量之比即为电池的健康状态。
为了证明该方法对于不同电池的适用性,选用一块国外某厂商生产的三元锂离子电池重复上述建模过程,此电池初始容量为36 Ah,490次循环容量衰退约3.026 Ah(8.55%),使用主成分回归建立容量估计模型,其模型公式为
模型表达式系数的正负号合理,其容量估计误差如图7所示。图7(b)显示所有循环的残差与误差值均控制在0.7 Ah(约2%)之内,证明了此模型的准确性和适用性。
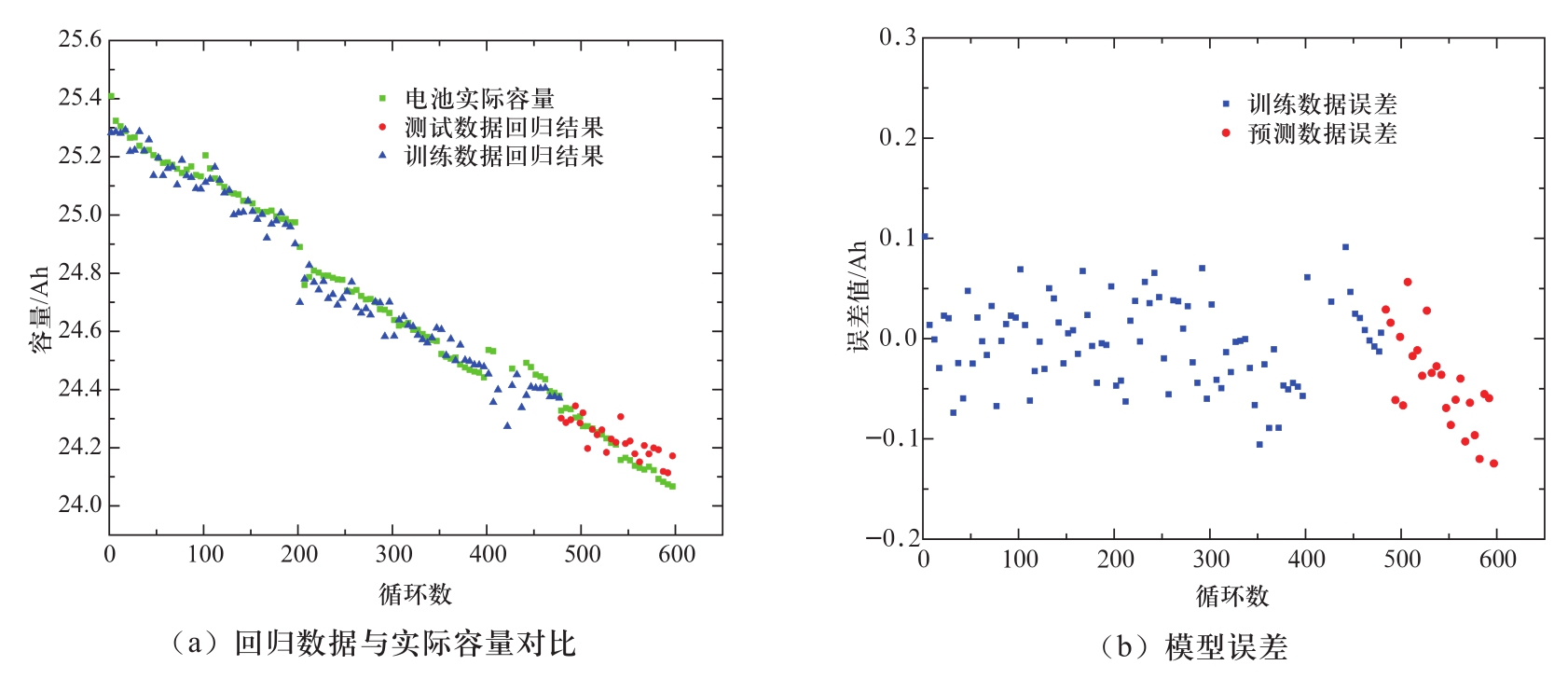
图6 三元锂离子电池容量估计模型准确度
Fig. 6 Accuracy of a LNMCO lithium-ion battery capacity estimation model
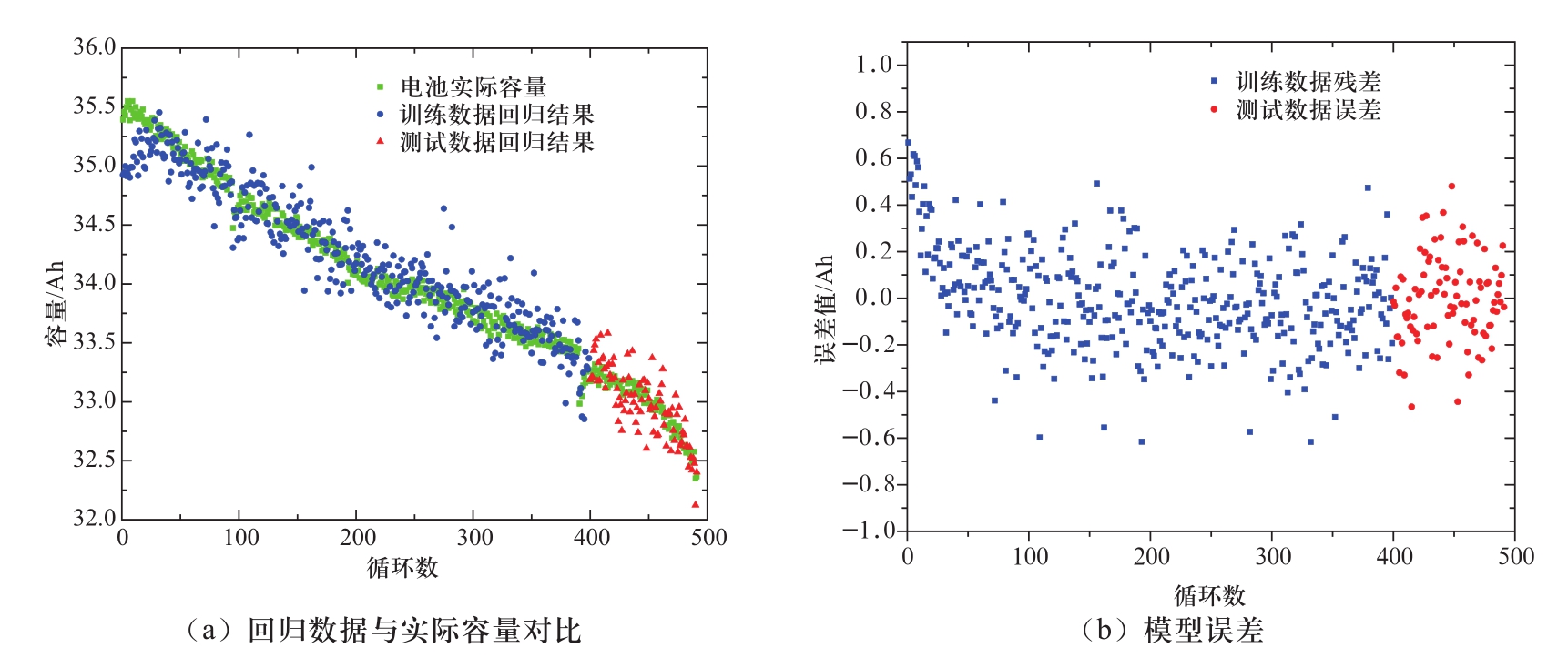
图7 36 Ah三元锂离子电池容量估计模型准确度
Fig. 7 Accuracy of a 36 Ah LNMCO lithium-ion battery capacity estimation model
4 基于主成分回归的容量估计模型与多元线性回归的比较
使用最常用的多元线性回归方法对数据进行回归分析,将其结果与上述基于主成分回归的健康状态估计模型结果作对比[16]。
用原6个参数作为多元线性回归模型的自变量,实际容量为模型因变量,训练多元线性回归模型,得到回归模型表达式为
式中,x1~x6 与公式(8)相同,分别表示I峰高度、II峰高度、II峰面积、II峰位置、II峰左斜率、II峰右斜率。
将主成分回归结果与多元线性回归模型进行比较。在准确度方面,两种方法的准确度基本相同,均在0.2 Ah(2%)以内。在解释性方面,多元线性回归的结果表达式不合理,在公式(9)中,代表II峰高度的x2的系数为负,而事实上,从表1可知,容量与II峰高度为正相关关系,因此这两个参数的系数正负号是不合理的,说明多元线性回归没有解决多重共线性问题,此方法造成了模型失真,无法解释电池的物理意义;相反地,主成分回归的结果表达式解释性非常好,每个参数的符号与相关性完全对应,因此在保证准确度的情况下解决了共线性问题。
5 结论
本文研究了锂离子电池的健康状态(SOH),在传统的以当前容量与出厂容量之比定义健康状态的基础上,使用容量增量曲线判断电池的老化衰退模式,获得了较好效果。由于锂离子电池的容量增量曲线(IC曲线)具有反映电池衰退机理和老化模式的优点,研究了三元锂离子电池容量增量曲线的变化与老化衰退之间的关系,提取IC曲线中多个特征参数,并从数据质量与实际应用两个方面对特征参数进行简化,建立了电池容量估计模型。由于多个特征参数之间存在很严重的多重共线性,因此选择主成分回归方法作为模型的回归方法,将估计误差控制在2%以内。将最后的容量估计结果与最常用的多元线性回归方法结果进行比较,在模型参数合理性和解释性方面体现出明显优势。
参考文献
[1] 李勇, 王丽芳, 廖承林. 电动车锂离子电池健康状态模型研究进展[J]. 电源技术, 2013,37(5):863-866.
Li Yong, Wang Lifang, Liao Chenglin. Advances of State of Health Modeling of Lithium-ion Battery for Electric Vehicles.Power System Technology, 2013, 37(5): 863-866(in Chinese).
[2] 周秀文. 电动汽车锂离子电池健康状态估计及寿命预测方法研究[D]. 长春:吉林大学, 2016.
[3] 姜久春, 马泽宇, 李雪,等. 基于开路电压特性的动力电池健康状态诊断与估计[J]. 北京交通大学学报自然科学版,2016,40(4):92-98.
Jiang Jiuchun, Ma Zeyu, Li Xue, et al.State of Health Diagnosis and Estimation of Power Lithium-ion Batteries Based on Open Circuit Voltage Characteristic[J]. Journal of Beijing Jiaotong University, 2016, 40(4): 92-98(in Chinese).
[4] 张立强. 锂离子电池多物理模型参数辨识及健康特征提取[D]. 哈尔滨:哈尔滨工业大学, 2015.
[5] 张锋, 张金, 高安同,等. 基于模型的锂离子电池健康状态预测[J]. 电子技术应用, 2014,40(12): 79~81.
Zhang Feng, Zhang Jin, Gao Antong, et al.Li-ion Battery State-of-Health Prognostic Based on Model[J]. Power Supply Technology and Its Application, 2014, 40(12): 79~81(in Chinese).
[6] 刘江波. 基于内阻检测的锂离子电池健康状态估计研究[D].武汉:武汉理工大学, 2015.
[7] Qin T, Zeng S, Guo J, et al. State of Health Estimation of Li-ion Batteries with Regeneration Phenomena: A Similar Rest Time-Based Prognostic Framework[J]. Symmetry, 2016, 9(1): 4.
[8] Torai S, Nakagomi M, Yoshitake S, et al. State-of-health Estimation of LiFePO4/graphite Batteries Based on a Model Using Differential Capacity[J]. Journal of Power Sources,2016, 306: 62-69.
[9] Dubarry M, Truchot C, Cugnet M, et al. Evaluation of Commercial Lithium-ion Cells Based on Composite Positive Electrode for Plug-in Hybrid Electric Vehicle Applications.Part I: Initial characterizations[J]. Journal of Power Sources,2011, 196(23):10336-10343.
[10] Zhang C, Jiang J, Zhang L, et al. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery[J]. Energies, 2016, 9(11): 900.
[11] 吴惠祥, 朱剑英, 左洪福. 磨粒特征参数的筛选及权分析[J].南京航空航天大学学报, 2002,34(5):442-445.
Wu Huixiang, Zhu Jianying, Zuo Hongfu. Screen and Weight Analysis of Wear Particle Characteristic Parameters[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2002,34(5): 442-445(in Chinese).
[12] Dubarry M, Liaw B Y. Identify Capacity Fading Mechanism in A Commercial LiFePO4 cell[J]. Journal of Power Sources,2009, 194(1): 541-549.
[13] 马雄威. 线性回归方程中多重共线性诊断方法及其实证分析[J]. 华中农业大学学报(社会科学版),2008(2):78-81.
Ma Xiongwei. Diagnosis and Empirical Analysis on Multicollinearity in Linear Regression Model[J]. Journal of Huazhong Agricultural University(Social Sciences Edition),2008(2): 78-81(in Chinese).
[14] Pearson K, Galton F. Pearson Product-moment Correlation Coefficient[J]. Covariance, 2014.
[15] 郭呈全, 陈希镇. 主成分回归的SPSS实现[J]. 统计与决策,2011(5): 157-159.
Guo Chengquan, Chen Xizhen. Using SPSS to Achieve Principal Component Regression[J]. Statistics and Decision,2011(5): 157-159(in Chinese).
[16] 罗文海, 万巧云, 高永. 主成分回归分析与多元线性回归的对比研究[J]. 数理医药学杂志, 2003,16(2):140-143.
Luo Wenhai, Wan Qiaoyun, Gao Yong. A Comparative Study of Principal Component Regression Analysis and Multiple Linear Regression[J]. Journal of Mathematical Medicine, 2003,16(2): 140-143(in Chinese).
Incremental Capacity Curve Based State of Health Estimation for LNMCO Lithium-ion Batteries
GUO Qi-pei1,2, ZHANG Cai-ping1,2, GAO Yang1,2, JIANG Jiu-chun1,2, JIANG Yan1,2
(1. National Active Distribution Network Technology Research Center (NANTEC) (Beijing Jiaotong University),Haidian District, Beijing 100044, China;2. Collaborative Innovation Center of Electric Vehicles in Beijing, Haidian District, Beijing 100044, China)
Abstract: The state of health (SOH) of lithium-ion batteries is a comprehensive evaluation index of battery aging, and characterization and SOH estimation are the key technology of the next generation of battery management system. The variation characteristics of LiNi1/3Mn1/3Co1/3O2(LNMCO)batteries’ incremental capacity curve (IC curve) with the aging of batteries are studied, and the characteristic parameters of the IC curves closely related to the battery ageing mechanisms are analyzed. The capacity estimation model of LNMCO lithiumion battery to indicate batteries’ SOH is established. To resolve the serious multicollinearity among the character parameters,the capacity estimation model based on the principal component regression is proposed. The experimental results demonstrate that the estimated errors are less than 2%. Using the parameters reflecting the electrochemical characteristics of the batteries,the proposed method can not only estimate SOH of the battery,but also identify the aging mode of the battery, providing the foundation for battery life management strategy.
Keywords: lithium-ion battery; state of health; capacity estimation; principal component regression
基金项目:国家重点研发计划项目(2016YFB0101801);国家电网公司科技项目“新一代电池管理系统关键技术研究”。
Project Supported by National Key Research and Development Program of China (2016YFB0101801) and Project Supported by Science and Technology Foundation of SGCC ‘Research on Key Technology of New Generation Battery Managment System’.
作者简介:

郭琦沛
郭琦沛(1993),男,硕士,主要研究方向为电动汽车动力锂离子电池建模及数据挖掘,E-mail:bjtuev@bjtu.edu.cn。
张彩萍(1982),女,教授,博士生导师,主要研究方向为电动汽车动力电池和储能电池在电力系统中的应用研究,E-mail:zhangcaiping@bjtu.edu.cn。
(责任编辑 赵杨)
