0 引言
输电线路的覆冰和积雪威胁着电力系统的安全运行,其中覆冰导线脱冰跳跃问题是输电线路设计需要深入开展研究的内容之一[1]。特高压输电线路导线截面较大,重冰区线路覆冰量大,脱冰时更容易引起较大幅度的跳跃[2]。导线脱冰跳跃是影响重冰区特高压输电线路设计的重要因素。由于中国国内对于重冰区特高压输电线路脱冰跳跃仍缺少系统的研究,本文通过建立计算机仿真模型,结合输电导线非线性动力模型,通过仿真计算,研究重冰区特高压输电线路导线脱冰跳跃特性,并对特高压塔头设计提出建议。
1 导线脱冰跳跃计算机仿真原理
仿真计算做出如下假设:1)只考虑导线张力,不考虑其弯曲和扭转的刚度;2)将导线分成若干导线单元段;3)导线的质量集中在导线的节点上;4)质点间连接为没有质量的弹性元件;5)各质点在空间(X、Y、Z)内平动(3自由度),不考虑导线的扭转;6)导线采用悬链线方程。
在上述模型中,除了考虑导线的内力(张力),还需要考虑导线在运行环境中可能承受的一系列外力,如分布于整个导线长度的载荷:自重载荷、覆冰载荷、风载荷等;集中在导线若干节点上的外力:悬挂点绝缘子串的拉力等[3]。
计算过程中,首先给定导线张力、弧垂的初始值,在X、Y、Z方向上,分别利用如下的差分方程递推求解出架空导线的完整运动过程。
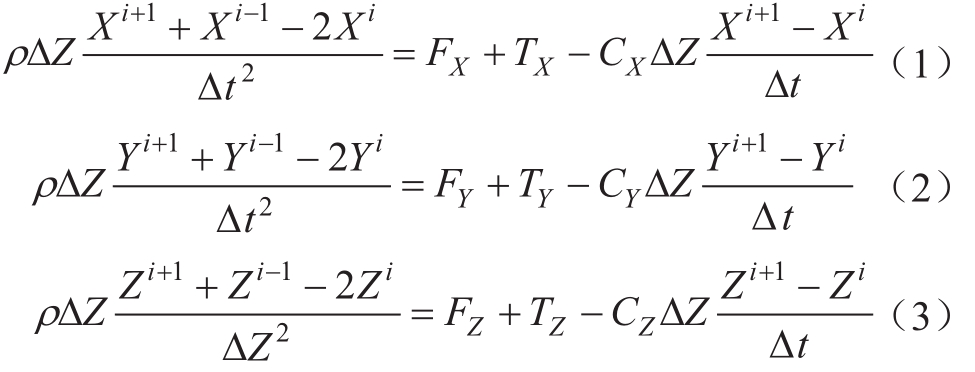
式中,ρ 为导线的单位长度质量,kg/m;Xi、Yi、Zi分别为导线上质点在i时刻 X、Y、Z方向上的位移,m;FX、FY、FZ分别为导线上质点在i时刻 X、Y、Z方向上的合外力,N;TX、TY、TZ分别为导线上质点在i时刻X、Y、Z方向上的张力合力,N;CX、CY、CZ 分别为导线在X、Y、Z方向上运动的阻尼系数,N/(m/s);∆t为时间差分间隔,s;∆Z为导线长度差分(导线单元段)长度,m。
当满足如下的Von Neumann条件时,求解过程可能收敛
式中,Tmax为导线上质点所受外力的最大值,N。
2 导线脱冰跳跃计算机仿真计算
2.1 档距大小和导线参数的影响
影响脱冰跳跃高度最直接的因素是相邻杆塔距离,即线路档距[4]。本文考虑 Y-Y-X-Y-Y 档距组合情况(5档),其中X为脱冰档,Y为非脱冰档。Y 取400 m,覆冰厚度取15 mm,脱冰比为50%,在不考虑高差的情况下,8分裂LGJ-630/55导线脱冰跳跃高度变化曲线如图1所示。
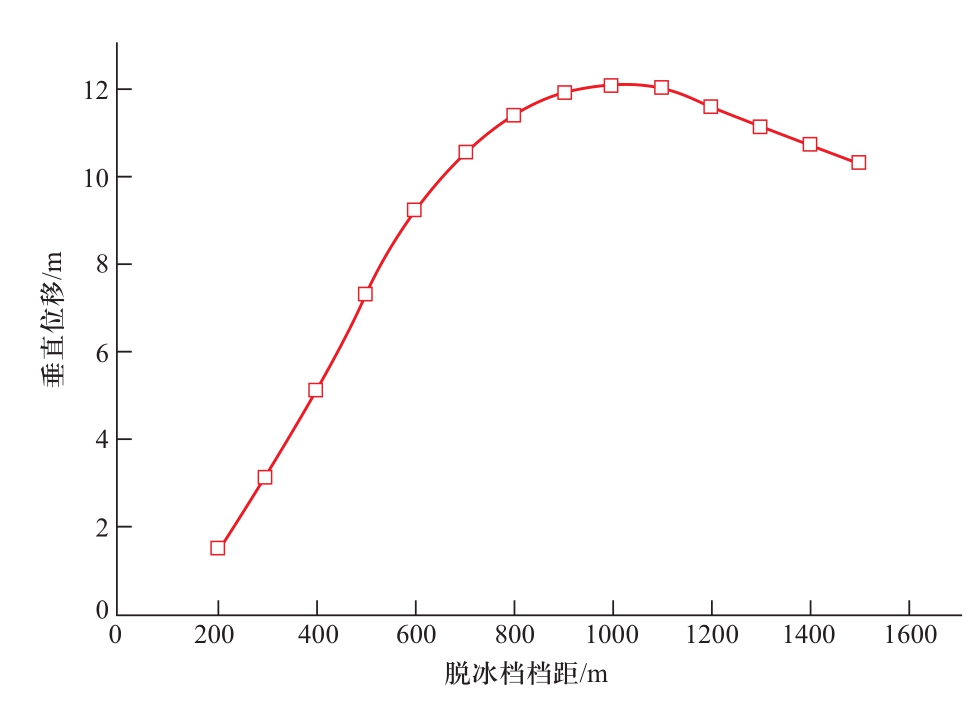
图1 档距大小对脱冰跳跃高度的影响
Fig. 1 Influence of span length on ice-shedding height
从图1可见,在档距较小的时候,脱冰跳跃高度随档距近似线性增长;档距较大后,跳跃高度呈现出饱和的趋势;档距进一步增大时,跳跃高度随档距增大反而减小。总体来说,跳跃高度随档距呈现出峰形的变化规律,存在一个跳跃高度的峰值。该峰值出现的档距与不同的档距组合有关,对于该计算实例,峰值出现在档距约为1000 m处,该档距大于重冰区线路绝大多数档距,因此可以认为:减小档距对于减小重冰区线路脱冰跳跃高度是有益的。
2.2 覆冰量的影响
仍考虑5档组合,Y取400 m,脱冰比为50%,覆冰为15 mm,在不考虑高差的情况下,LGJ-630/55导线的脱冰跳跃高度变化曲线如图2所示。
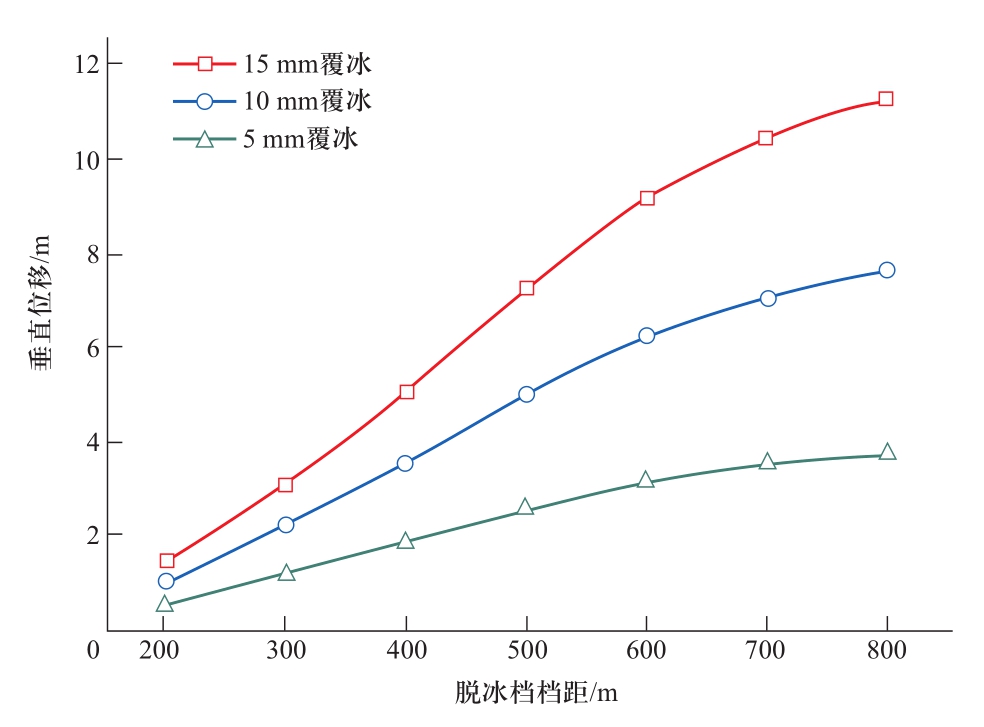
图2 覆冰厚度与导线脱冰跳跃高度的关系
Fig. 2 Relationship between ice thickness and ice-shedding height
从图2可见,覆冰量越大,导线脱冰跳跃高度也越大,两者基本呈线性关系。可见,在选择输电线路路径时,应尽量避开重冰区,减小导线覆冰量,减少因导线脱冰引起的工程投资。
2.3 脱冰比的影响
当脱冰比分别为25%、50%、75%、100%,且均匀脱冰时,LGJ-630/55导线脱冰跳跃高度变化曲线如图3所示。
从图3可见,随着脱冰比的增加,导线脱冰跳跃高度明显增加,当脱冰比为100%时,导线脱冰跳跃高度比脱冰比为50%时高出近2倍,可见均匀脱冰时,脱冰比的取值非常重要。在输电线路设计时,应根据线路重要性及覆冰特点综合考虑脱冰比取值。按照《重覆冰架空输电线路设计技术规程》规定,在校验静态接近距离时,330 kV及以上重冰区线路可选不小于设计冰重的80%进行设计,330 kV及以上中冰区线路可选不小于设计冰重的70%进行设计。结合上述计算,对于特高压工程,推荐重、中冰区均采用100%脱冰数据进行校验。
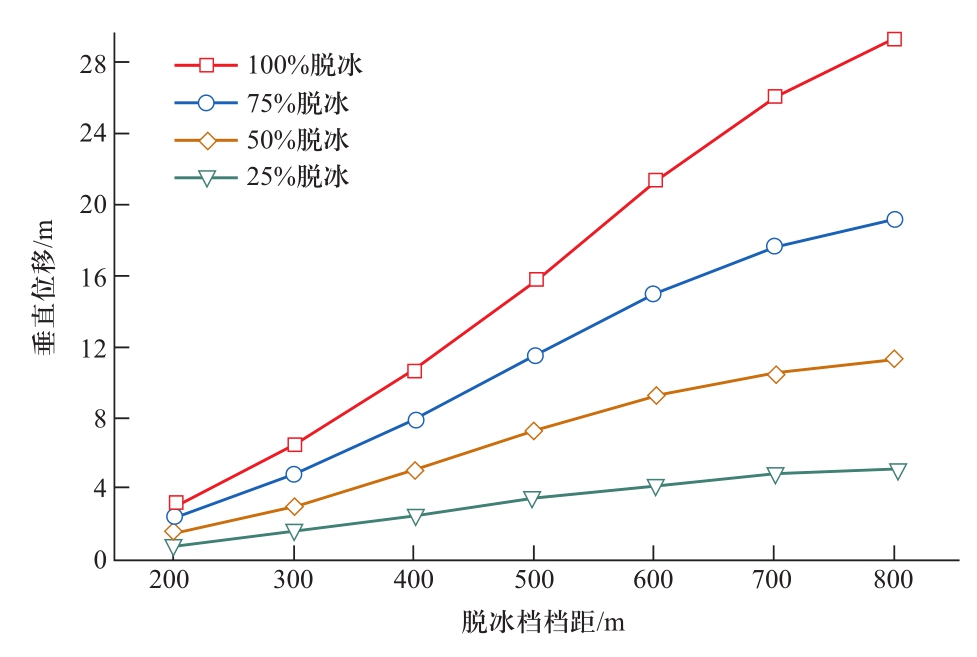
图3 脱冰比对脱冰跳跃高度的影响
Fig. 3 Influence of ice-shedding ratio on ice-shedding height
2.4 档距组合的影响
研究表明,多档连续时,其中1档发生覆冰脱落,脱冰跳跃高度要明显高于该档为孤立档时的脱冰跳跃高度[5-6]。对于连续2档的情况,由于导线两端受耐张串约束,且在连续档中档数最少,因此是连续档中脱冰跳跃高度最低的。各种档距组合下,覆冰15 mm、50%脱冰比、无高差时,LGJ-630/55导线脱冰跳跃变化曲线如图4所示。
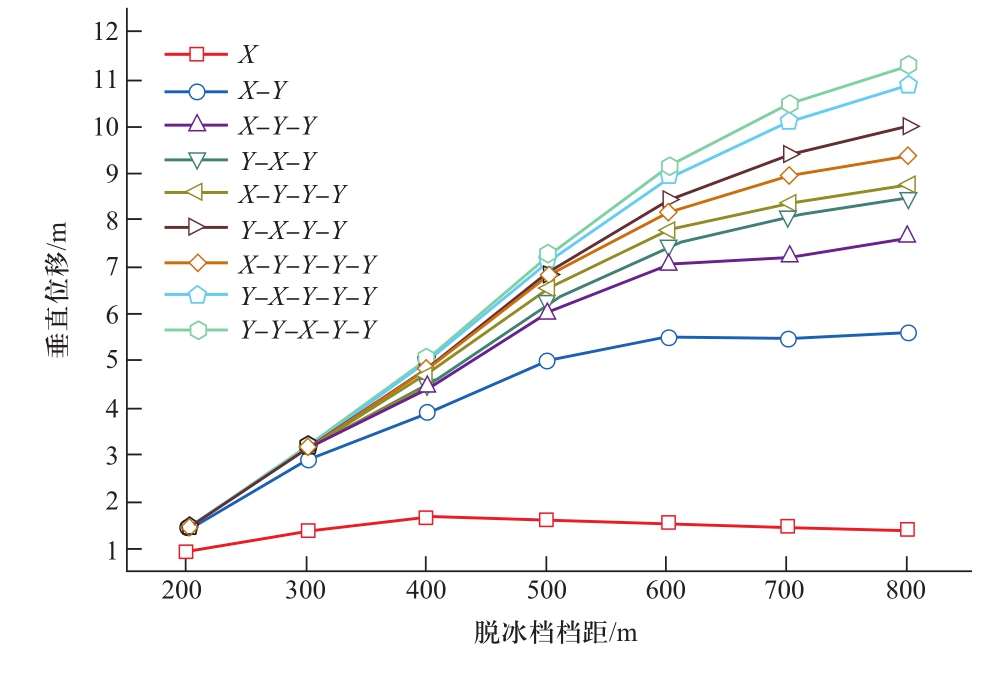
图4 导线脱冰跳跃高度与档距组合的关系(X为脱冰档,Y为非脱冰档,Y=400 m)
Fig. 4 Relationship between ice-shedding height and span combination, where X is ice shedding span, and Y is non-shedding span, Y equals 400 m
从图4中至少可以得出以下结论:
(1)与连续档相比,孤立档的脱冰跳跃是最不严重的。
(2)在耐张段内档数不超过5档时,脱冰跳跃高度随档数增加而增大,更多档数有待进一步研究。
(3)当档数较少时,(2)中的影响较大;当档数达到一定程度时,上述影响趋于饱和。
(4)越靠近连续档中间的档,脱冰跳跃高度越大,越靠近耐张塔的档,脱冰跳跃高度越小。
由此可见,在重冰区线路设计时,应该注意:1)连续档靠近中央档的脱冰跳跃校验;2)直线塔的脱冰跳跃比耐张塔更为严重;3)可通过直线开断来改善脱冰跳跃,且连续档越少,改善效果越明显。
2.5 不均匀脱冰的影响
仍考虑 Y-Y-X-Y-Y 的档距组合,档距均为400 m,覆冰厚度取15 mm,在不考虑高差的情况下,LGJ-630/55导线发生50%不均匀脱冰的跳跃高度,如图5所示。
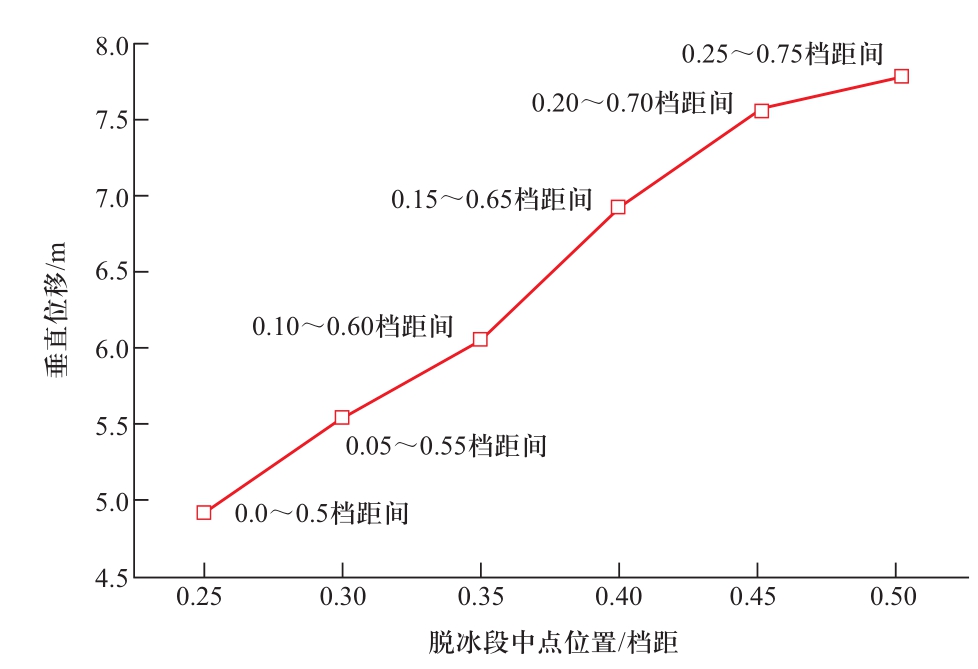
图5 不均匀脱冰对脱冰跳跃高度的影响
Fig. 5 Influence of uneven ice-shedding on ice-shedding height
可见,在相同的脱冰比下,脱冰位置越靠近档距中央,其跳跃高度越大。通过对比图1可知,发生50%的不均匀脱冰比100%均匀脱冰更严重。是否考虑不均匀脱冰、不均匀脱冰的位置以及脱冰比的取值均会对工程设计造成较大影响,该设计取值是值得进一步研究的课题[7-8]。
2.6 高差的影响
考虑5档组合,X取800 m,Y取400 m,50%均匀脱冰,覆冰厚度取15 mm,在脱冰档存在30%高差的情况下,研究LGJ-630/55导线发生脱冰跳跃情况。
研究发现,当有高差存在时,脱冰档中点的跳跃方向与无高差的情况不同[9-10]。导线不仅会沿垂直方向跳跃,还会沿纵向跳跃,即发生斜向跳跃。导线垂直、纵向位移随时间变化的动态过程如图6所示。
档距中点在纵向—垂直平面内的跳跃运动轨迹如图7所示。
该斜向跳跃轨迹近似为一条直线,将其与无高差情况下的结果进行比较可以看出,其运动轨迹幅度与无高差时基本相当,从而等效垂直跳跃高度比在无高差的情况下小。因此,在线路设计时无需专门考虑地形高差对脱冰跳跃的影响。
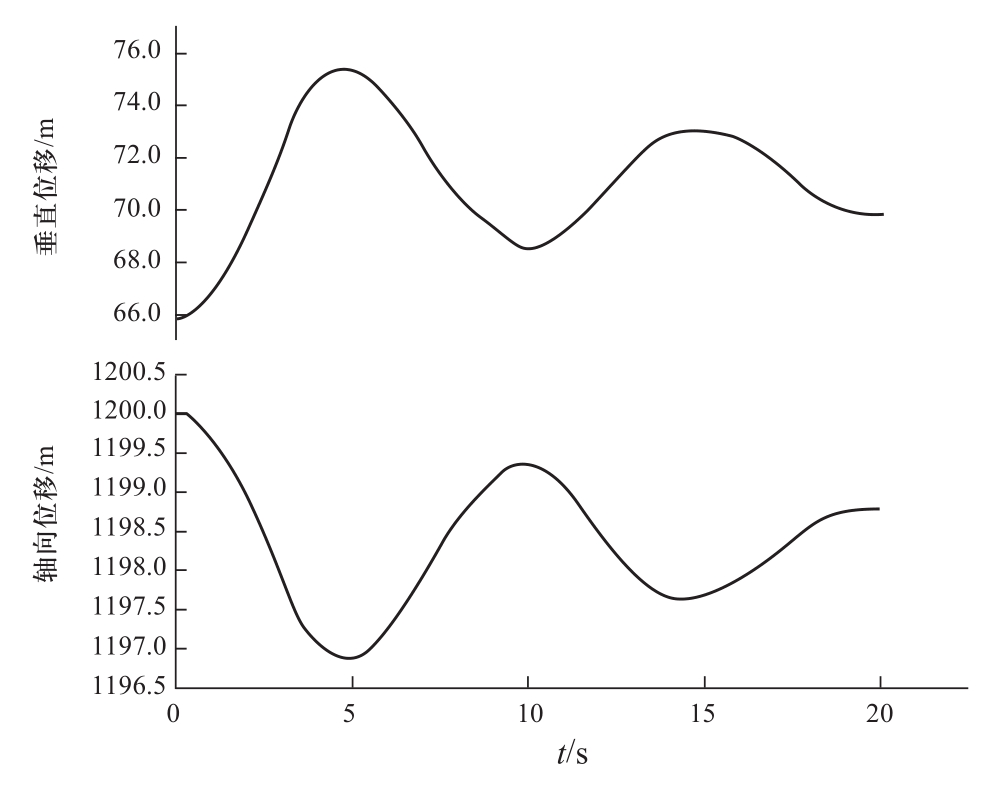
图6 有高差时的档距中点位移
Fig. 6 Displacement of the middle point of the span as height difference exists
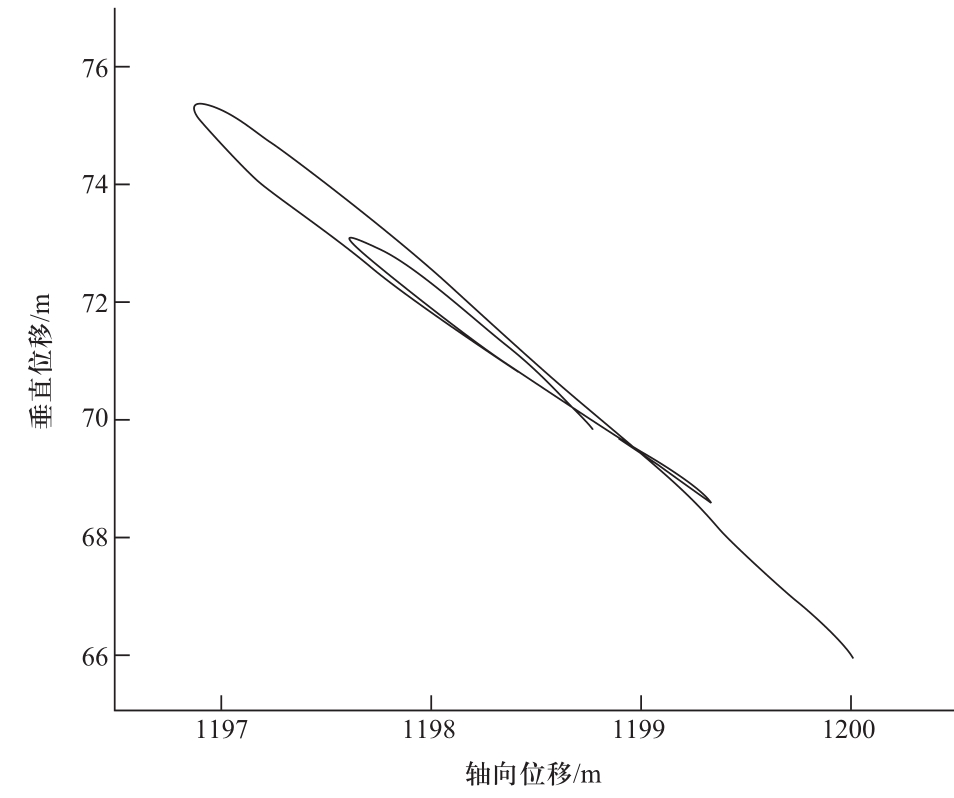
图7 档距中点的跳跃轨迹(30%高差)
Fig. 7 Movement trace of the middle point of the span(30% height difference)
2.7 风速的影响
风速对导线脱冰跳跃也有一定的影响。结合已建重冰区特高压线路的经验,覆冰厚度取15 mm,风速取0、10 m/s时,LGJ-630/55导线的脱冰跳跃轨迹如图8所示。图中左侧垂直的直线轨迹为无风时的脱冰跳跃轨迹,右侧是有风时的脱冰跳跃轨迹。
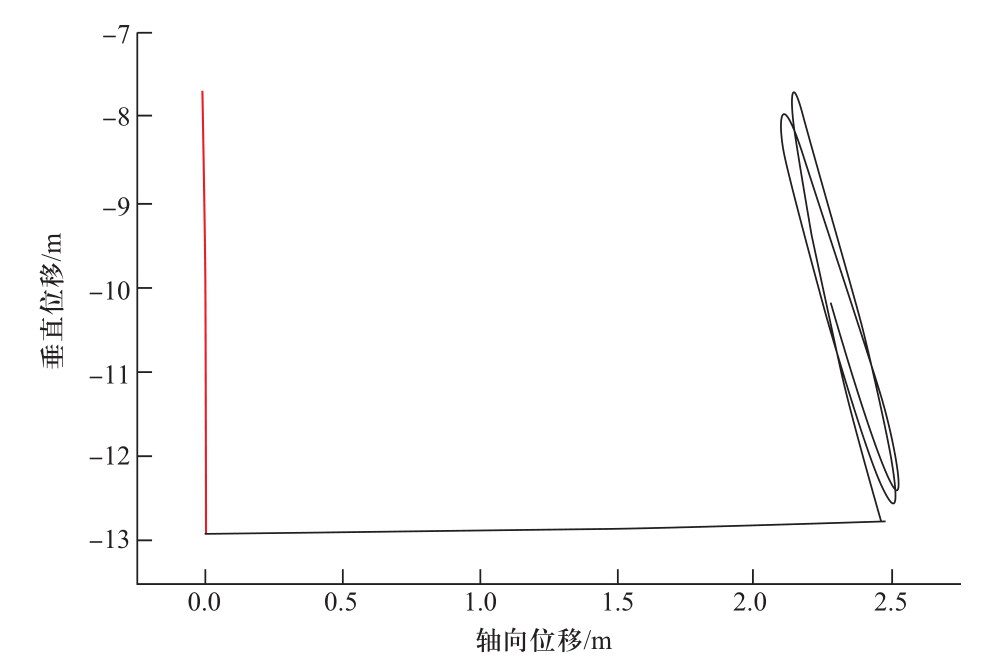
图8 风对脱冰跳跃水平及垂直位移的影响
Fig. 8 Influence of wind on ice-shedding height and vertical displacement
由此可见,在有风的情况下,导线脱冰跳跃轨迹不仅沿垂直方向有位移,沿水平方向也有一定位移,该位移值与考虑的风速有关。本实例水平位移计算值约为2.5 m。从下文第3.2节可见,该计算结果可能是导(地)线水平偏移的影响因素之一。
2.8 不同导线的影响
结合特高压常用的LGJ-630/45、LGJ-630/55、LGJ-800/55 3种导线,计算在5档组合下,15 mm覆冰、无高差时的脱冰跳跃高度,其变化曲线如图9所示。

图9 不同导线的脱冰跳跃高度
Fig. 9 Ice-shedding height of different conductor types
由图9可见,LGJ-630/45导线的脱冰跳跃高度最高,LGJ-800/55导线的脱冰跳跃高度最小。可见,刚性越强的导线跳跃高度越小;而同样刚性的导线单重越重,跳跃高度越小。虽然如此,应注意到由导线变化引起的脱冰跳跃高度增加很小,因此可以认为:对于重冰区特高压输电线路,仅为了减少导线脱冰跳跃影响而选择大截面、大钢芯导线是不经济的。
3 对输电线路塔头设计的影响
对于特高压输电线路,脱冰跳跃是塔头设计的重要影响因素之一。对于同塔双回线路,脱冰跳跃不仅影响导线层间距和地线支架高度,还影响相邻导线或导地线水平偏移。
3.1 对导(地)线层间距的影响
根据计算,线路覆冰分别为5、10、15 mm时,连续5档线路均匀/不均匀脱冰(50%)情况下导线脱冰跳跃高度如表1~3所示。
表1 均匀脱冰和不均匀脱冰情况下导线脱冰跳跃高度(5 mm设计覆冰)
Table 1 Ice-shedding height of conductors under even and uneven ice-shedding (5 mm ice thickness)

表2 均匀脱冰和不均匀脱冰情况下导线脱冰跳跃高度(10 mm设计覆冰)
Table 2 Ice-shedding height of conductors under even and uneven ice-shedding (10 mm ice thickness)
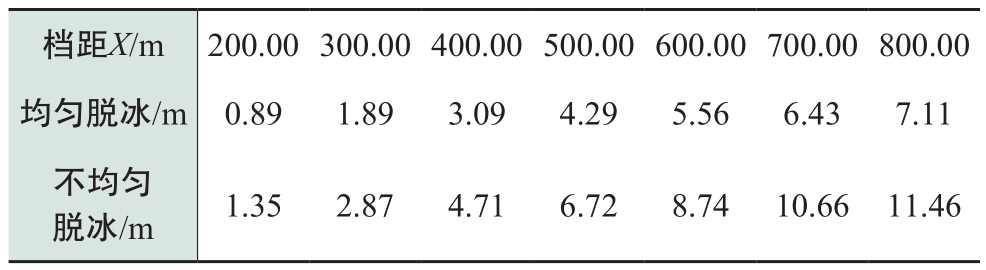
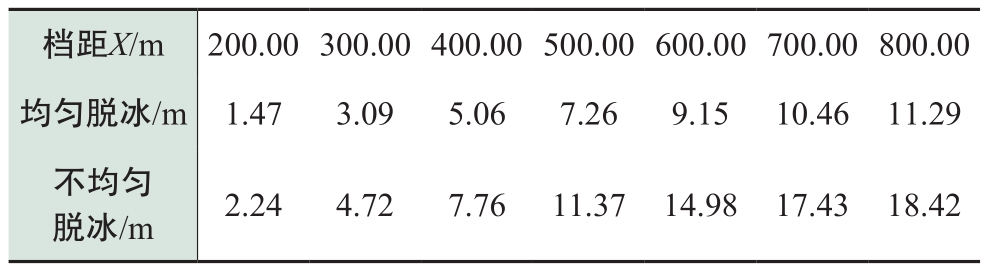
表3 均匀脱冰和不均匀脱冰情况下导线脱冰跳跃高度(15 mm设计覆冰)
Table 3 Ice-shedding height of conductors under even and uneven ice-shedding (15 mm ice thickness)
按照GB 50665—2011《1000 kV架空输电线路设计规范》第8.0.1条条文规定:“垂直线间距离主要是确定于覆冰脱落时的跳跃,因此是与弧垂及冰厚有关的。根据实际运行经验,垂直线间距离较相同的水平线间距离可以小一些,即允许的弧垂或档距可以大一些……根据我国双回路线路运行经验,推荐垂直线间距离可为水平线间距离的0.75倍。”第8.0.1条规定:“使用悬垂绝缘子串的杆塔,其最小垂直线间距离宜符合表8.0.1.2的规定(16 m)或取水平线间距离的75%。”
由表1~3的计算结果可以看出,当覆冰15 mm、考虑50%脱冰、脱冰档档距为800 m时,脱冰跳跃高度达到18.42 m。该值已超过规程规定的16 m。即使考虑相邻导线水平偏移和其他因素,也无法满足电气间隙要求。由于规程未规定计算脱冰跳跃时对应的脱冰率、覆冰厚度、均匀/不均匀脱冰情况,因此可以认为,设计规程是考虑到大多数情况(如档距较小、中冰区或轻冰区)下的规定值,但实际工程中,若出现大档距、重覆冰等特殊情况,应根据实际地形、工程条件进行脱冰跳跃计算,并结合线路安全等级确定合理的导(地)垂直线间距。
3.2 对导(地)线水平偏移的影响
导线脱冰跳跃还会影响导(地)线水平偏移值。按照GB 50545—2010《110 kV~750 kV架空输电线路设计规范》规定:“覆冰地区上下层相邻导地线间或地线与相邻导线间的最小水平偏移,宜符合表8.0.2的规定(对750 kV、10 mm覆冰为2 m)。”根据GB 50665—2011《1000 kV架空输电线路设计规范》第8.0.2条:“上下层相邻导线间或地线与相邻导线间的最小水平偏移,重覆冰地区宜根据工程设计覆冰厚度、脱冰率、档距等条件计算确定。”按照DL/T 5440—2009《重覆冰架空输电线路设计技术规程》:“……杆塔上应有足够的垂直线距和水平位移,以满足导线与地线或导线之间在不同期脱冰时静态和动态接近的电气间距要求。静态接近距离不应小于操作过电压的间隙值,动态接近距离不应小于工频电压的间隙值。”
可以看出,上述规程均未明确规定1000 kV线路的相邻导线或导地线间水平偏移。按照GB 50665—2011《1000 kV架空输电线路设计规范》第8.0.2条规定:“在1000 kV晋东南—南阳—荆门交流特高压试验示范工程设计中,按75%脱冰计算,导地线间水平偏移从0~4 m,脱冰跳跃动态接近要求导地线间最大垂直投影距离约0.6 m。考虑到导线的分裂半径,该线路导地线间水平偏移取1 m。”
根据本文计算,当覆冰为15 mm、覆冰同时风速为10 m/s时,LGJ-630/55导线脱冰跳跃水平位移可能达到2.5 m。导地线水平偏移值与脱冰跳跃的关系图如图10所示。
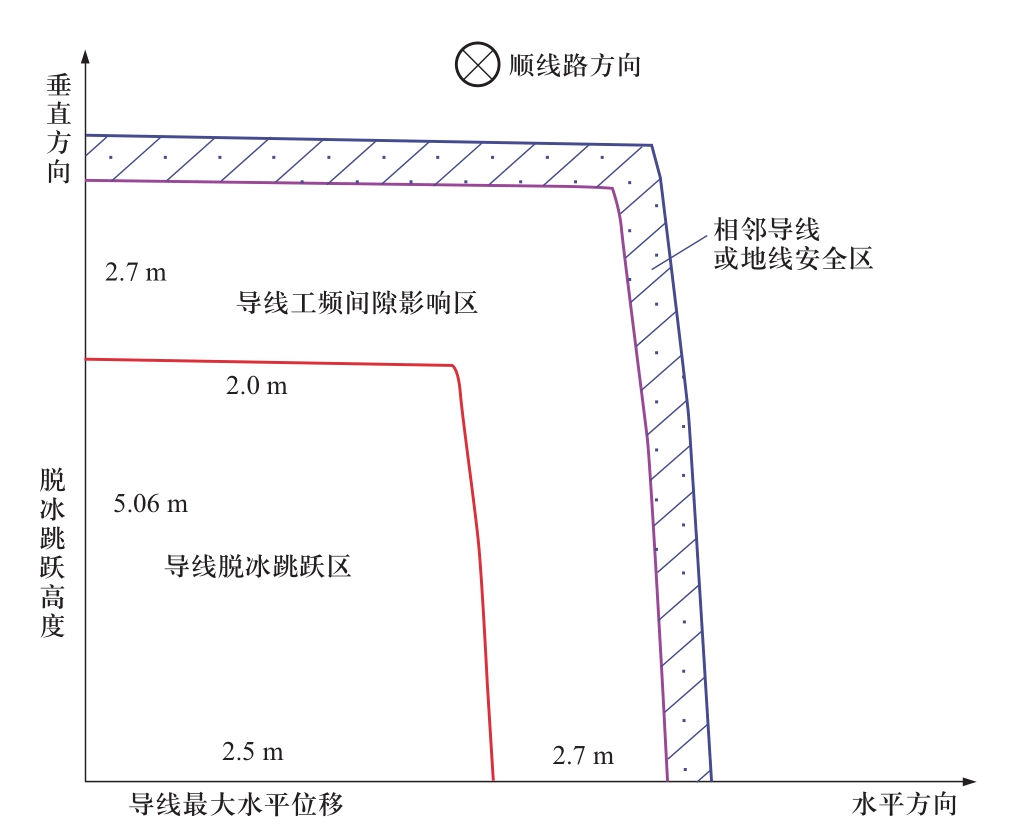
图10 脱冰跳跃对水平偏移的影响
Fig. 10 Influence of ice-shedding on horizontal deviation of conductor
从图10可以看出,导线脱冰跳跃区实际上近似为梯形。考虑工频电压间隙值(1000 kV、500 m海拔,约为2.7 m),导(地)线水平偏移值可选择0~5.2 m(2.5 m+2.7 m),不同的水平偏移,垂直距离也不同,工程设计中应结合雷电保护角、导地线档中防雷距离等因素共同确定该水平偏移值[11]。
4 结论
(1)通过建立计算机仿真模型,结合输电导线非线性动力模型,通过仿真计算,研究重冰区特高压输电线路导线脱冰跳跃特性。
(2)由计算结果可见,导线脱冰跳跃与档数、档距、覆冰量、脱冰比、高差、风速等多种因素相关:1)在耐张段内档数不超过5档时,档数越多,脱冰跳跃越严重;2)在档距小于1000 m时,档距越大,脱冰跳跃越严重;3)覆冰量越多,脱冰跳跃越严重;4)脱冰比越多,脱冰跳跃越严重;5)高差越大,垂直脱冰跳跃高度越小;6)风速越大,脱冰跳跃水平位移值越大。
(3)脱冰跳跃应作为导(地)线垂直距离、水平偏移值的确定因素之一。对于重冰区特高压输电线路,推荐绘制导线脱冰跳跃图,结合动态和静态跳跃特性共同确定合理的导(地)线安全距离。
参考文献
[1] 蒋兴良,易辉.输电线路覆冰及防护[M].北京:中国电力出版社,2002:97-102.
[2] 刘和云.架空导线覆冰与脱冰机理研究[D].武汉:华中科技大学,2001:34-37.
Liu Heyun.Research On Icing And Shedding Mechanism Of Overhead Transmission Lines[D]. Wuhan: Huazhong University of Science and Technology, 2001: 34-37(in Chinese).
[3] Lott J N, Sittell M C.The February 1994 Ice Storm In The Southeastern U.S.[C]//Proceedings Of The 7th International Workshop On Atmospheric Icing Of Structures (IWAIS).Quebec, Canada: 1996: 127-128.
[4] Eskandarian M.Ice Shedding From Overhead Electrical Lines By Mechanical Breaking: A Ductile Model For Viscoplastic Behaviour Of Atmospheric Ice[D].Quebec: University of Quebec at Chicoutimi, 2005: 125-127.
[5] Jamaledding A.Weigh-Dropping Simulation Of Ice-Shedding Effects On An Overhead Transmission Line Model[C]//Proceedings Of The 7th International Workshop On Atmospheric Icing Of Structures (IWAIS).Quebec, Canada: 1996: 77-82.
[6] Barbieri R, Barbieri N, De Souza Júnior O H.Dynamical Analysis Of Transmission Line Cables.Part 3—Nonlinear Theory[J].Mechanical Systems and Signal Processing, 2008,22(4): 992-1007.
[7] Kálmán T, Farzaneh M, Mcclure G.Numerical Analysis Of The Dynamic Effects Of Shock-Load-Induced Ice Shedding On Overhead Ground Wires[J].Computers & Structures,2007, 85(7): 375-384.
[8] Jamaleddine A, Mcclure G, Rousselet J, et al.Simulation Of Ice-Shedding On Electrical Transmission Lines Using ADINA[J].Computers & Structures, 1993,47(4-5): 523-536.
[9] 邵天晓.架空送电线路的电线力学计算(第二版)[M].北京:中国电力出版社,2003:111-113.
[10] 国家电力公司东北电力设计院.电力工程高压送电线路设计手册[M].北京:水利电力出版社,2002:201-203.
[11] 侯镭,王黎明,朱普轩,等.特高压线路覆冰脱落跳跃的动力计算研究[J].中国电机工程学报,2008,28(6):1-6.
Hou Lei, Wang Liming, Zhu Puxuan, et al.Dynamic Behavior Computation Of Ice Shedding Of UHV Overhead Transmission Lines[J]. Proceedings of the CSEE, 2008, 28(6): 1-6(in Chinese).
Research on Ice-shedding and Tower Head Design for UHV Overhead Transmission Lines in Heavy Icing Area
ZHAO Yuan-tao1, LYU Jian-shuang1, LI Jian1, MENG Xiao-bo2
(1. Central Southern China Electric Power Design Institute, Wuhan 430074, Hubei Province, China;2. Department of Electrical Engineering Tsinghua University, Haidian District, Beijing 100084, China)
Abstract: Nonlinear model of conductor is adopted in this article, together with the actual situation of UHV overhead transmission lines in heavy icing area, to conduct computer modeling. Finite element analysis is used to calculate the relationship of the span number, span length, ice thickness, iceshedding ratio, height difference, wind speed and other factors with ice-shedding of conductor. Qualitative analysis is made on the influence factors of ice-shedding of conductor. Proposals are given for engineering design. Calculation results show that the ice-shedding height increases with the increase of span number that is smaller than 5 in the tension section; the longer the span length is, the more serious is the ice-shedding when the span length is smaller than 1000 m; the larger the height difference is, the smaller is the vertical jump height of a transmission line after ice-shedding; the horizontal displacement of ice-shedding is larger as the wind speed increases. Based on the calculation results, suggestions are provided for determining the layer distance between conductors and ground wire and the horizontal displacement in tower head design.
Keywords: heavy icing area; UHV overhead transmission lines;ice-shedding; tower head design
作者简介:

赵远涛
赵远涛(1985),男,硕士,高级工程师,主要从事输电线路设计与研究工作,E-mail:zhaoyuantao@csepdi.com。
吕健双(1987),男,硕士,工程师,主要从事输电线路设计与研究工作,E-mail:ljs5469@csepdi.com。
李健(1981),男,硕士,高级工程师,主要从事输电线路设计与研究工作,E-mail:lijian@csepdi.com。
(责任编辑 赵杨)
