0 引言
当前电力电子技术的迅速发展及电网中电力电子器件的大量引入使得电力系统中许多计算和控制问题日益复杂。在一定程度上来说,电力试验几乎是不可能直接进行的,因此适时地、合理地借助电力系统的仿真技术是非常必要的。而电力系统仿真技术对计算机运行速率以及数值计算方法具有较强的依赖性。随着计算机技术的不断发展,电力系统仿真技术成为电力系统规划、保护、调度甚至故障研究的重要工具,同时仿真结果的准确性对指导电力系统安全、可靠、经济运行具有重要的影响,而仿真结果的准确性主要依赖于基础算法的研究工作。
目前电力系统仿真技术基础算法有大量的研究成果,当前较为成熟的电力系统仿真平台中使用的建模分析方法大体可分为:节点分析法(nodal analysis method)、状态空间法(state-space techniques)和状态空间节点法(state space nodal, SSN)。这三种分析方法使用不同的数值计算方法对电路进行求解。本文就这三类方法针对具体的RLC谐振电路仿真结果显现的差异性进行对比分析研究,展现各种算法之间的差异性。
1 三种方法基本原理简析
数值积分方法是电力系统暂态稳定性分析计算的基本方法。数值积分法主要分为显式数值积分法和隐式数值积分法。当用于求解微分方程时,显式算法求解是对时间进行差分,不存在迭代和收敛的问题,因此求解效率高,但计算精度不高,并需设定合适的时间步长求解以保证系统的稳定,较大或较小的时间步长都会导致求解时间很长;隐式算法求解与时间无关,采用的是牛顿迭代法,因此存在迭代收敛问题,这类算法的计算精度较高。
1.1 节点分析法
利用节点分析法进行电路求解的仿真软件统称为EMTP(Electromagnetic Transient Program)类软件。代表性的有离线仿真软件PSCAD/EMTDC、EMTPRV,实时数字仿真系统RTDS等。EMTP类软件的实质是利用隐式梯形法解算电路暂态参数的过程。对隐式梯形法的理解:
对于一常微分方程,即
在 t-Δt 到 t 积分步长内的隐式梯形积分公式为
隐式梯形法的核心思想是把网络中的所有元件模型都用不变的等值电阻和反映历史记录的等值电流源来代替。然后根据这个等值电路建立节点方程式,对其形成的导纳矩阵求逆,即可求出所需的解[1]。
隐式梯形积分法是电力系统仿真分析中行之有效的求解算法,主要由于它数值稳定性好,可以采用大步长,可通过联立求解同步发电机的差分方程和网络的代数方程来消除接口误差。但是,当电力网络中存在断路器操作时,采用这种方法将使非状态变量产生不正常的摆动,造成数值震荡。针对这种现象,研究人员将CDA(critical damping adjustment)引入到隐式梯形积分方法中,并取得较好的效果。
与显式数值积分法相比其计算量要大。经分析可知,隐式梯形积分法的误差小,局部截断误差为o(h(3)),且数值稳定性好。
1.2 状态空间法
状态空间法是通过状态变量描述来建立系统内部状态变量与外部输入变量和输出变量之间的关系。状态变量法属于一般性建模方法,列出的电路状态方程和输出方程组成为

式中,A为系统矩阵,B为输入矩阵,C为输出矩阵,D为直接传递矩阵,它们是由系统的结构和参数所定出的常数矩阵。典型的应用状态空间法求解电路的仿真软件有Simulink、PLECS等。以Simulink为例,其数值分析方法具体来分包含两大类:显式Runge-Kutta(RK)方法和隐式刚性解法[2-5]。
Runge-Kutta (RK)方法可以构造高阶精度的方法来求解初值,同时可以避免函数f的偏导数计算。
低阶显式RK法通常通过半离散化的方法来求解偏微分方程,但目前对于系统中含有初值问题的常微分方程通常倾向于采用中高阶来解决。针对一个系统来考虑时,稳定性要比精确度更重要。而显式RK方法中,高阶RK法的稳定性要比低阶稳定性差。所以对于低精度要求的系统采用低阶方法更有效。
Simulink中汇集了各种求解常微分方程数值的方法,这些方法分为两大类:可变步长类算法和固定步长类算法。在相同的误差允许条件下,变步长计算可以降低计算次数、缩短仿真时间。另外变步长仿真计算可以提供误差控制和过零检测,应用较为广泛。
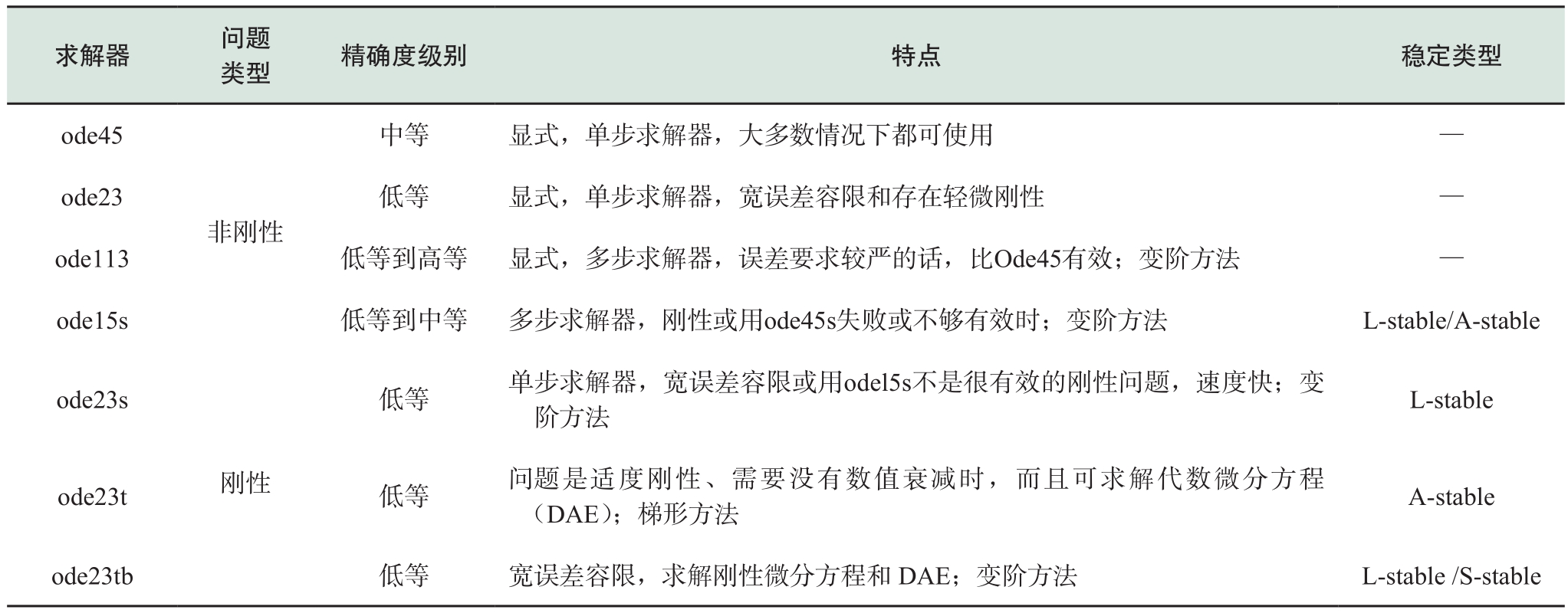
Simulink提供了7种连续的变步长常微分方程求解器: Ode45、Ode23、Ode113、Ode15s、Ode23s、Ode23t、Ode23tb。
另外,Simulink中包含2种离散的常微分方程求解器:Backward Euler和Tustin。这两种算法也属于隐式—龙格库塔法。
Backward Euler(后向欧拉法)是一种具有较高稳定性的算法(L-稳定,属于A-稳定范畴),并且由于其差分方程中不出现t-Δt时刻的非状态变量,在此过程中不会因为非状态变量的突变产生等值注入源,因此该算法不会产生数值震荡。但是,相比于隐式梯形积分法,后向欧拉法的精度要差。
Tustin算法又称梯形法或双线性变换(A-稳定)。从误差或者精度的角度考虑,Tustin算法要优于欧拉法。
表1 各变步长求解器的适用条件[4,7~10]
Table 1 Applicable conditions of solvers with variable step size[4,7~10]
1.3 状态空间节点法
实时数字仿真软件RT-LAB是在Matlab/Simulink的基础上发展而来的,通过对电路进行并行处理达到实时化的目的。对于一个没有长输电线、节点密集、电力电子设备种类和数量众多的电力系统,利用传统的电力系统模型解耦方法很难保证在确定的步长和精度的前提下完成模型的解算。RT-LAB在状态空间模型的基础上,结合节点分析法的优点,提出专门针对以状态空间方程建模的大系统解耦方法—状态空间节点法 [11-13]。
SSN建模方法的基本原理是将电路模型分割成若干任意大小的子网络,并使用状态空间法对各子网络进行建模和计算,求解出各个子网络的等效电路。在各个子网络之间使用经典的节点法建立即时求解的节点网络方程,并在同一个仿真步长内,对各个子网络所解算出的等效电路进行联解得到整个电路的全局结果。这样就避免了解耦所带来的人为延时,并提高了仿真的精度和数值稳定性。
另外,适当的划分状态空间群组,不但可以有效减少系统的等效电气节点数,还能减小每个群组的开关数量及预计算量,节省存储空间,加速仿真。由于子网络的规模较小,因此子网络内部可以采用高阶的算法进行状态空间方程的求解,例如RT-LAB中常用的ARTEMIS“art5”算法。考虑到稳定性,art5法具备L-稳定性(属于A稳定范畴),使得art5算法能够抵抗类似梯形算法的不稳定性的产生,在消除数值振荡方面有一定的优势。
2 案例分析
本文中采用了带有阶跃信号控制理想开关的RLC谐振电路来验证三种平台(PSCAD/EMTDC,Simulink,RT-LAB)中不同数值算法之间的差异,如图1所示。RLC串联谐振电路及参数设置为:串联电阻R=1×10-4Ω,串联电感L=1×10-5 H,串联电容C=6×10-6F,阶跃信号发生器的设置为Step Time为0.1s。EMTDC、Simulink以及RT-LAB中的离散算法设置的步长均为Δt=1×10-5s,Simulink中的连续模型设置的最大步长限制为Δt=1×10-4s。其中示波器输出的是电容器C两端的电压Uc。图2为采用RT-LAB中的SSN建模方法给出的RLC模型。
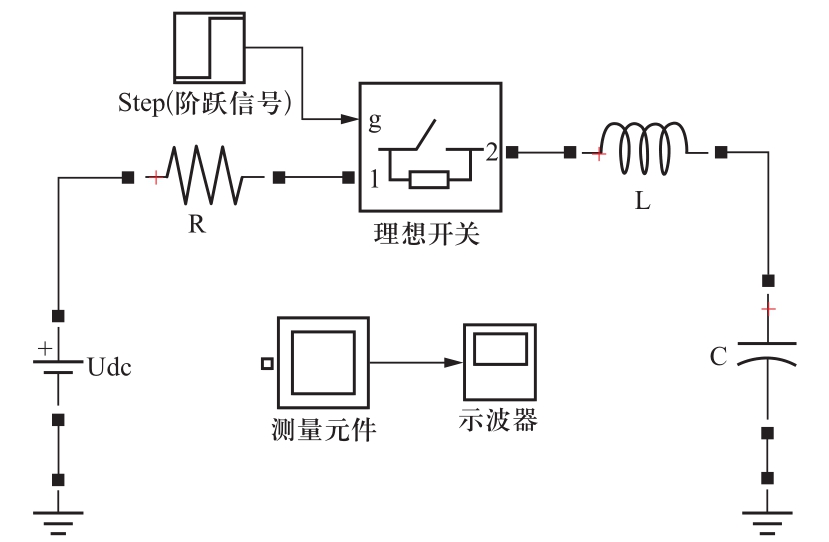
图1 RLC串联谐振电路及参数设置
Fig. 1 RLC series-resonant circuit and parameter setting
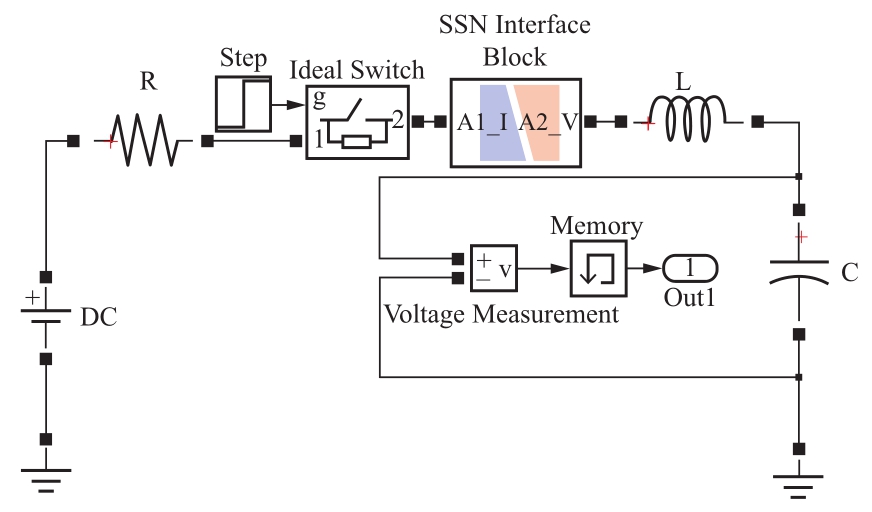
图2 RT-LAB仿真测算模型
Fig. 2 RLC model simulated by RT-LAB
根据已知的电路,当理想开关闭合后,可以得到该电路的微分方程:
将式(4)转化为状态空间方程可得:

状态空间方程离散化后的精确解为:
为了获得离散的表达式,需要对矩阵指数eA∆t进行估计。分别利用隐式梯形法、后退欧拉法和art5算法对矩阵指数进行近似:
(1)隐式梯形积分法
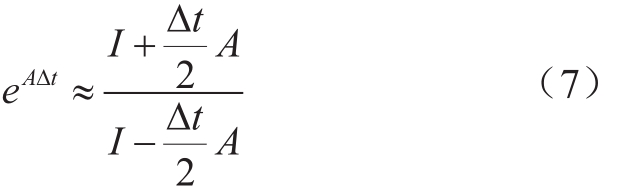
(2)后退欧拉法
(3)art5算法
通过对RLC谐振电路进行离散化后可知,基于不同的仿真算法,系统最后得到的递归方程不同,从而拥有不同的收敛速度和暂态过程。下面对不同仿真算法的仿真结果进行对比分析。
3 结果分析
对上述电路以及对应参数列出的微分方程进行求解,可得其解的形式如下:
带入所测得的两个点,可求解常数C1、C2的值。
针对三种仿真平台中的不同算法进行设置,图3~图6分别给出了4种不同离散算法:EMTDC中的隐式积分算法、Simulink-Discrete中的两种状态空间法(Tustin、Backward Euler)以及RT-LAB中的art5算法的解算结果,其中图5插图给出了局部的放大效果。
测试结果表明,不同的解算方法得到的解算结果差异性较大。
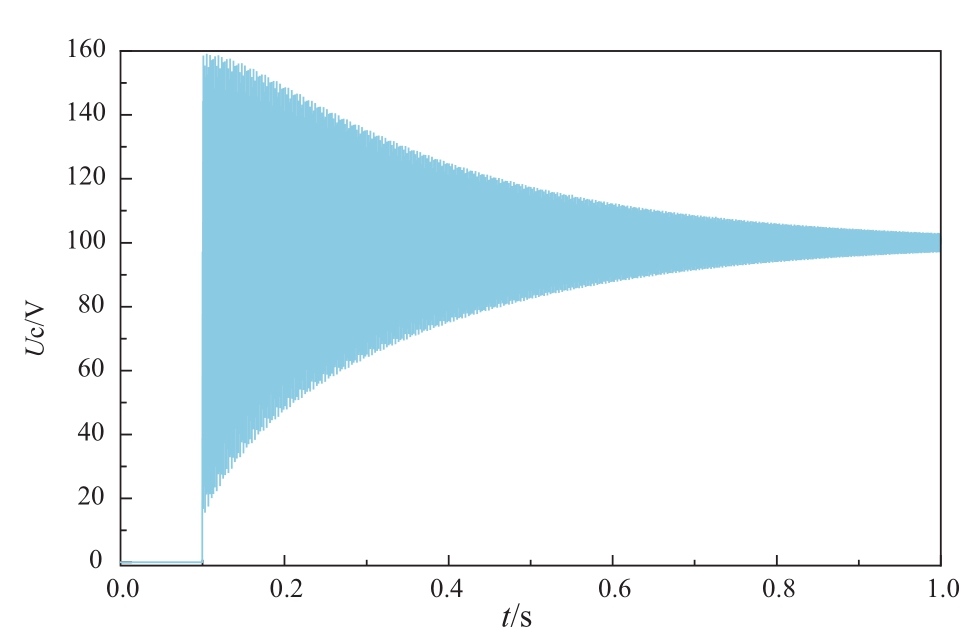
图3 EMTDC的解算结果
Fig. 3 Simulation results of EMTDC
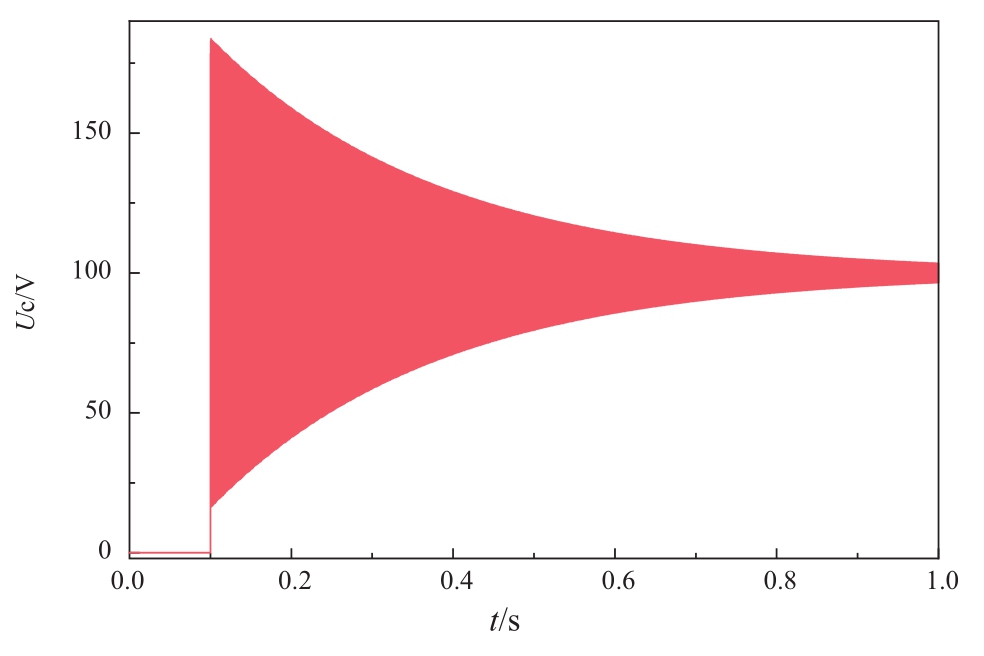
图4 Tustin的解算结果
Fig. 4 Simulation results of Tustin
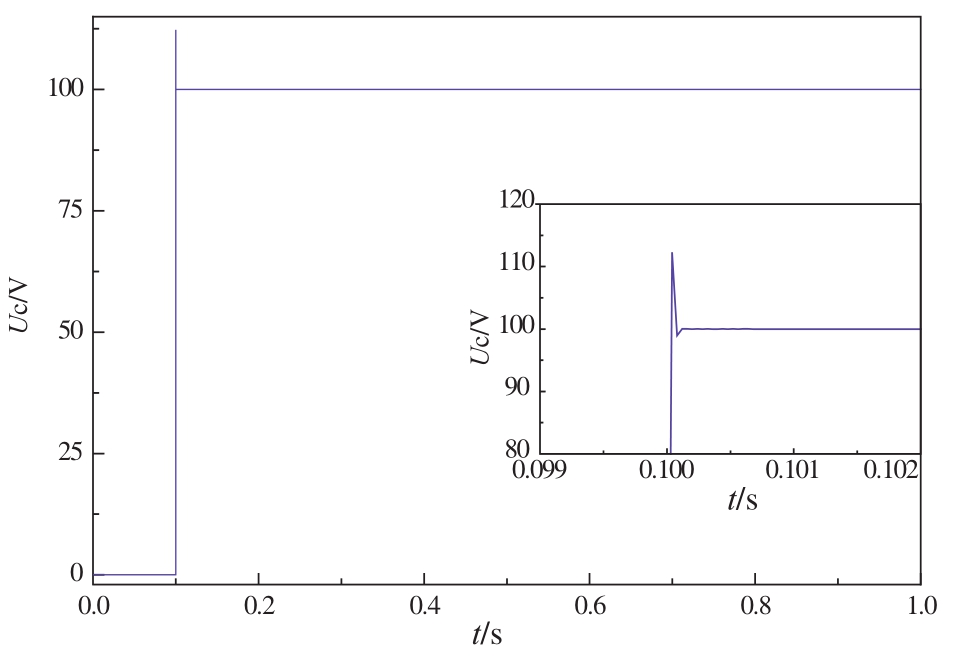
图5 Backward Euler的解算结果
Fig. 5 Simulation results of Backward Euler
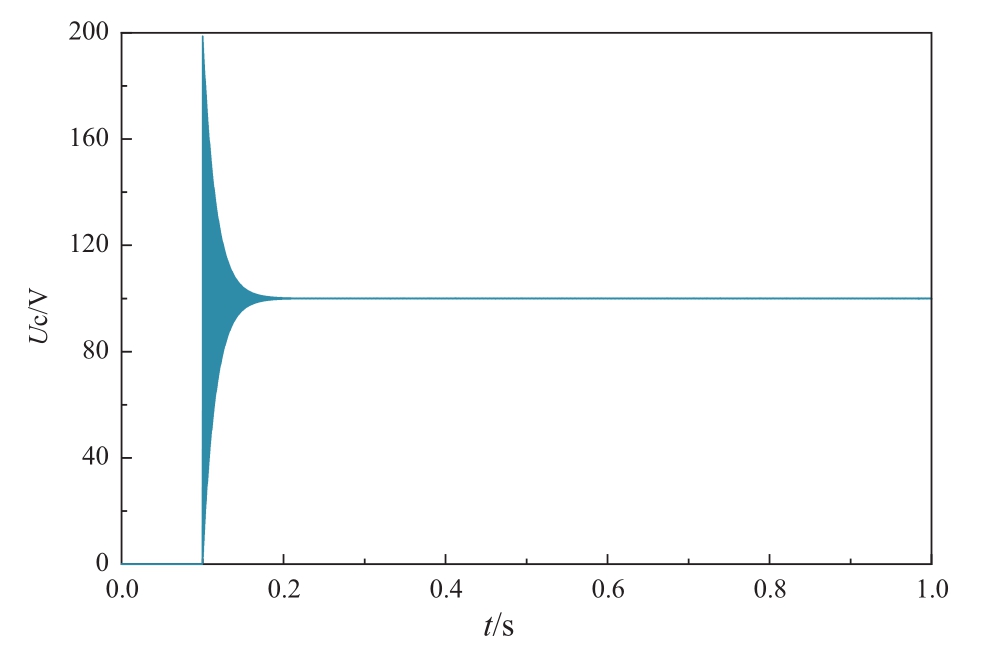
图6 Artemis中的SSN求解结果
Fig. 6 Simulation results with SSN solvers
通过与理论推导结果进行对比,EMTDC方法(二阶隐式梯形积分法)的仿真结果和基于Simulink平台的Tustin算法(二阶隐式梯形积分法)与真解相近,且二者给出的仿真结果的形貌差别不大(电路电气振荡频率、相位和衰减及振荡衰减后的稳态值),但振荡初始幅值存在差异。
art5算法在振荡的幅值上差异更为明显,同时与真解相比,art5算法能够较为迅速地衰减电路中产生的数值振荡(100 ms内原型震荡衰减完毕),art5为一种L稳定算法,其特性会衰减较高频率的原型振荡,此外,可能与SSN建模方法使得在同一个仿真步长内将计算分为两个阶段计算而又未采用迭代计算有一定的关系。
如上所述,Backward Euler在此过程中不会因为非状态量的突变而产生等值注入源,能够对数值振荡起到很好的抑制效果。
在Simulink仿真平台中,Ode15s、Ode23t、Ode23tb三种解算方法的参数设置中存在Solver reset method选项(Fast和Robust),根据不同的设置方式,得出的结果差异性较大。其中Ode15s和Ode23tb两种算法设为Fast条件下输出的结果出现了非常大的冲击值(此处结果并未列出),与正常解算值之间差别甚大,显著异于真解,因而报告只给Robust选项下的结果。图7给出了Ode15s、Ode23s和Ode23tb的解算结果。明显的,三种算法均未能给出准确的解,原型振荡明显不是按照指数规律衰减,与实际物理过程不符,算法加入了人为的衰减因子。
另外,Ode23t算法与真解相近,但原型震荡初始幅值偏大。
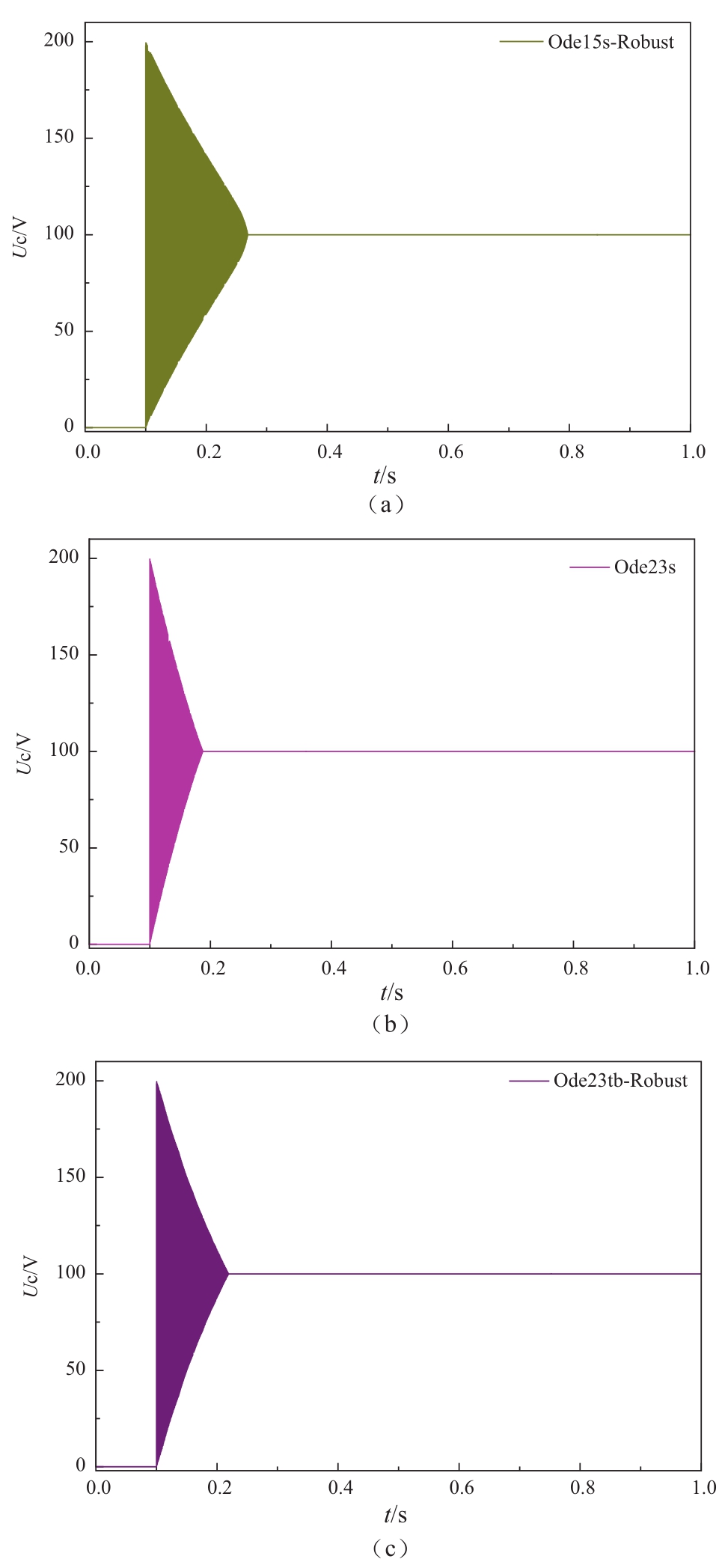
图7 Simulink中三种连续模式求解器的解算结果
Fig. 7 Simulation results of three kinds of continuous solvers in Simulink
此外,Ode23t算法在设置Solver reset method这一参数和限制最大步长的不同设置均存在较大差异,如图8所示,其中插图给出了仿真时间为1.0~2.0s时间段内的仿真结果输出波形。其中,图8(a)和图8(b)分别为Max step size设置为auto时的Fast和Robust仿真结果,图8(c)和图8(d) 分别为Max step size设置为1×10-4s时的Fast和Robust仿真结果,1.2~1.3s后原型振荡不再衰减,甚至稍有增幅并维持恒定幅值持续振荡,这是不合理的,主要是由于步长在较大的情况下截断和累积误差较大造成。
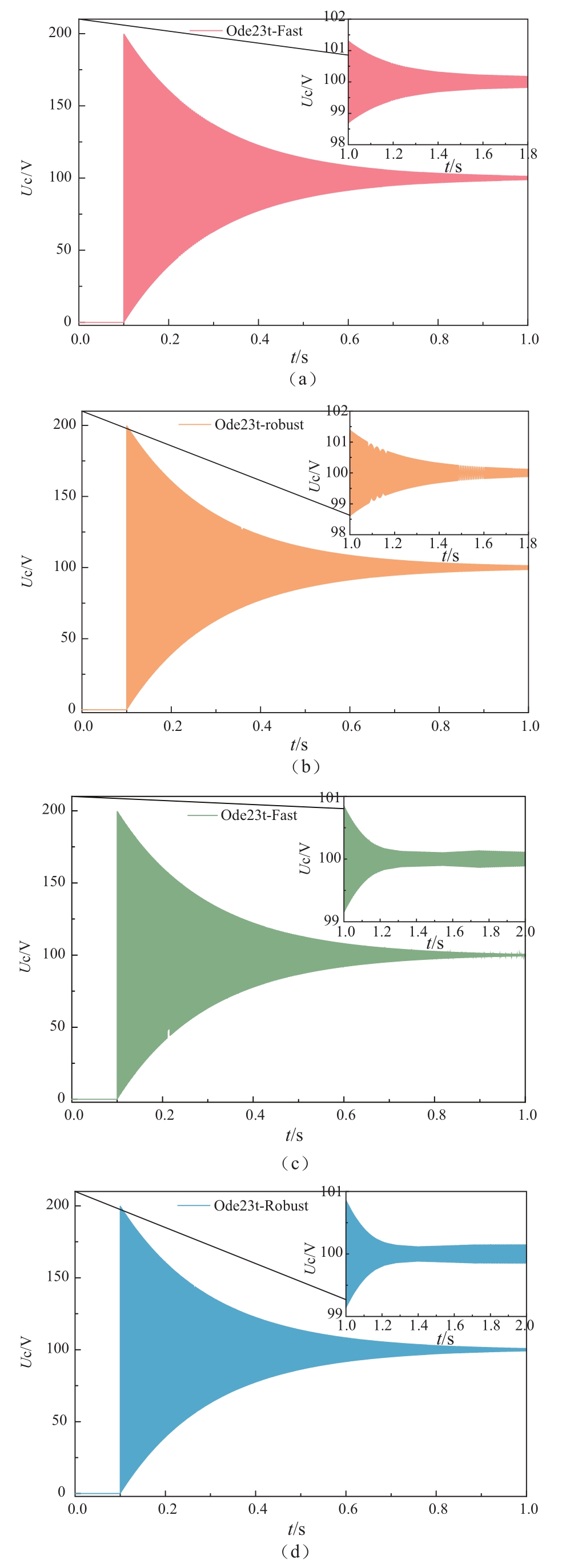
图8 不同条件设置下的Ode23t算法的仿真结果
Fig. 8 Simulation results of Ode23t that the parameters was set different
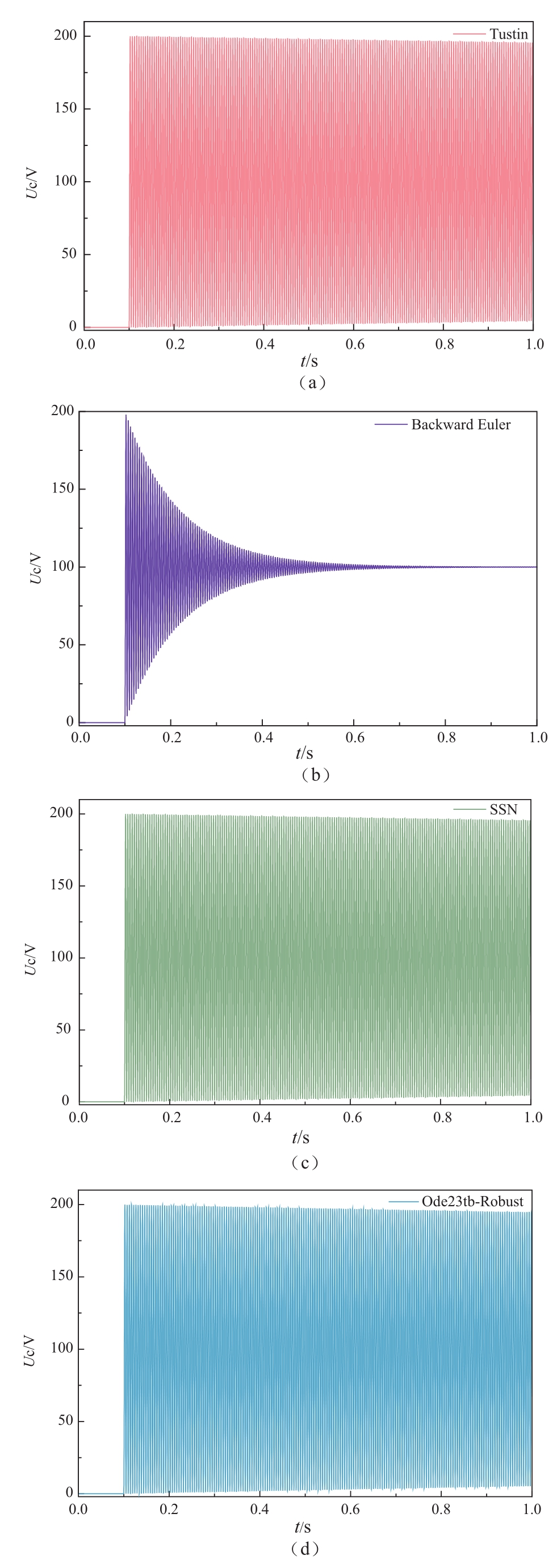
图9 低频RLC模型仿真结果
Fig. 9 Simulation results of low frequency RLC circuit
图9 给出了低频RLC模型仿真结果。其中RLC谐振电路模型参数为:串联电阻R=1×10-4Ω,串联电感L=1×10-3H,串联电容C=6×10-4F,阶跃信号发生器的设置为Step Time为0.1s,Max step size设置为1×10-4s。
结合前面的结果分析可以看出,Tustin算法针对高低频谐振电路的仿真结果并无明显差异,在处理低频电路时,其振荡衰减速度略低、震荡幅值略大;Backward Euler算法、SSN算法以及Ode23tb算法在处理高低频谐振电路的仿真时,其结果存在明显的差异:Backward Euler算法针对低频谐振电路的仿真时体现了电路的原型震荡的效果,且震荡幅值远大于对高频谐振电路,说明Backward Euler算法中采用的阻尼设置对高频电路有较强的抑制作用,对低频电路效果不佳,但相比其他几种算法,该方法中的振荡衰减速率最快;art5算法在低频谐振电路的仿真过程与Tustin算法的结果几乎相同,这是由于其均采用的是类梯形积分算法,此外,与处理高频谐振电路结果的差异性标明art5算法对高频谐振电路中产生的振荡有一定的抑制作用;Ode23tb的仿真结果代表了Max step size设定为1×10-4s时,Simulink/Continuous中四种算法(Ode15s、Ode23t以及O23tb均设为Robust模式)的解算结果,其与Tustin算法的解算结果相似。
4 结语
从上述对各种算法的介绍可知,每种算法都有各自的优缺点,针对不同的情况有各自独特的处理方式。但对于简单的RLC谐振模型时,不同的算法对模型开关事件的响应之间展现出显著差异,因此在后续工作中选择合适的算法是非常有必要的。另外,在Matlab/Simulink的使用中多种算法的参数设置对其结算结果的影响较大,这一现象值得我们的关注。RTLAB中采用的art5算法针对高频特性具有较强的抑制作用。Backward Euler算法采用的阻尼方法可以有效抑制高频振荡电路中产生的振荡,但对低频振荡电路产生的振荡起到的作用不明显。本文通过多种算法对RLC谐振电路的仿真结果分析,展现了各种算法在商用平台中针对同一开关事件处理结果的差异性。关于各种算法详细分析将会在后续工作中展开。
参考文献
[1] H. W. Dommel. 电力系统电磁暂态计算理论[M].李永庄,林集明,曾昭华,译. 北京:水利电力出版社,1991.
[2] Burden R L., Faires J D.. Numerical Analysis[M]. 北京:高等教育出版社. 2003:249-343.
[3] 关治,陆金甫. 数值分析基础[M]. 北京:高等教育出版社2013:342-393.
[4] Shampine L F, Reichelt M W. The MATLAB ODE Suite[J].Siam Journal on Scientific Computing, 1997, 18(1):1-22.
[5] Enright W H, Hull T E, Lindberg B. Comparing numerical methods for stiff systems of O.D.E:s[J]. BIT, 1975, 15(1):10-48.
[6] Ahmed W K. Advantages and Disadvantages of Using MATLAB/ode45 for Solving Differential Equations in Engineering Applications[J]. Computer Science Journals, 2013.7(1):25-31.
[7] Bogacki P, Shampine L F. A 3(2) pair of Runge - Kutta formulas[J]. Applied Mathematics Letters, 1989, 2(4):321-325.
[8] Lamba H, Stuart A M. Convergence results for the MATLAB ode23 routine[J]. BIT, 1998, 38(4):751-780.
[9] Shampine L F, Reichelt M W, Kierzenka J A. Solving Index-1 DAEs in MATLAB and Simulink[J]. Siam Review, 1999,41(3):538-552.
[10] Hosea M E, Shampine L F. Analysis and implementation of TRBDF2[J]. Applied Numerical Mathematics, 1996, 20(1):21-37.
[11] Dufour C, Mahseredjian J, BéLanger J, et al. An Advanced Real-Time Electro-Magnetic Simulator for power systems with a simultaneous state-space nodal solver[C]// São Paulo, Brazil:Transmission and Distribution Conference and Exposition:Latin America. IEEE. 2010:349-358.
[12] Dufour C, Mahseredjian J, Belanger J. A Combined State-Space Nodal Method for the Simulation of Power System Transients[J]. Power Delivery IEEE Transactions on, 2011,26(2):928-935.
[13] Dufour C, Tremblay O. Iterative algorithms of surge arrester for real-time simulators[C]// Wroclaw, Poland: Power Systems Computation Conference. IEEE. 2014: 18-22.
The Comparison and Study of Fundamental Algorithms in Power System Simulation
LIU Dong1,3,4 , TANG Shao-pu2, HU Xiang-nan1,4, ZHANG Shu-qing2, SHU De-wu2, HU Lu2, LU Jun-guang2
(1. Global Energy Interconnection Research Institute, Changping District, Beijing 102209, China;2. Department of Electrical Engineering of Tsinghua University, Haidian District, Beijing 100084, China;3. State Key Laboratory of Advanced Power Transmission Technology, Changping District, Beijing 102209, China;4. Beijing Key Laboratory of DC Grid Technology and Simulation, Changping District, Beijing 102209, China)
Abstract: The solution method of differential algebraic equations is the basis of power system simulation technology.The calculation methods of different solutions have different effects on the calculation results, which has an important influence on the calculation and analysis of the model. The three kinds of analysis methods which are mostly used in current commercial software platforms contains: the nodal analysis method for EMTP type software, the state space method in Matlab/Simulink and the state space node method for RTLAB platform. The paper describes the differences between the algorithms based on the simulation results of typical RLC model and analyzes the corresponding reasons of the differences combining with the characteristics of each algorithm.
Keywords: differential algebraic equation; implicit trapezoidal method; state-space method; state-space nodal
Project Supported by Science and Technology Foundation of SGCC(SGRIZLK J[2015]231).
作者简介:

刘栋
刘栋(1982),男,博士,高级工程师,研究方向为VSC-HVDC系统仿真技术研究。E-Mail:16039662@qq.com。
唐绍普(1988),男,硕士,工程师,研究方向为电力系统数字仿真、电力系统实时仿真。E-Mail:tangshaopu@126.com。
胡祥楠(1988),男,硕士,工程师,研究方向为柔性直流输电系统实时数字仿真。
张树卿(1983),男,助理研究员,博士,研究方向为电力系统数字仿真、电力系统实时仿真、电力系统负荷测辨建模。
(责任编辑 张鹏)
