0 引言
充分发展可再生能源,有效提高传统化石能源利用系统的效率,是能源可持续发展的必然选择[1-2]。然而,由于传统电、热等能源行业相对独立,单独规划运行与控制导致系统整体能源利用效率低,甚至影响可再生能源的消纳[3]。微能源系统集成了电、热、气等多种形式能源,并且多能流的转换、存储与传输存在互补特性,因此,对微能源系统进行综合能量管理,可协同控制与优化各能源系统,进而就近利用可再生能源,提升系统总能效[4-6]。
多能流传输、转换、存储过程的整体建模是实现微能源系统综合能量管理的基础。然而,传统模型往往将电、热、气各子系统分开考虑,不利于各能源系统间有机协调。因此,微能源系统整体建模近年来成为了研究热点[7-8]。在电力系统中,电能直接在电场作用下进行传输。然而,与电能传输不同,热能传输包含两类过程:一类是伴随着管道中的流体流动引起的热量输运;另一类则是在换热器中冷、热流体之间的传热过程。考虑到不同形式能量传输过程中存在非线性约束,部分研究在建立系统整体模型时简化了系统的非线性传输约束。例如,苏黎世联邦理工学院提出了能源枢纽(energy hub)概念来描述综合能源系统中电、热、气等多种形式能量之间的转换、传输、存储及利用等过程[9-10]。应用energy hub概念,文献[11]基于电力系统与热力系统中的能量平衡,在不考虑能量传输约束的前提下建立了微能源系统的整体模型。文献[12-13]在系统整体能量平衡的基础上,考虑了热网与电网的传输极限,并且通过给定传输损失系数考虑了传输过程中能量的损失[13]。文献[14]在利用直流潮流法考虑电能传输约束的基础上建立了综合能源系统模型,并对分布式能源系统进行了优化,但未考虑热力系统中的热能传输。文献[15]将传热过程的非线性约束简化为线性约束,考虑了热力系统中换热器的传热过程,但势必会存在误差。可见,以上研究均未完整反映微能源系统中电、热传输过程的非线性特征。然而,若要引入完整的热量传输模型,热量传输约束中存在的强非线性可能会给后续运行模拟及优化计算带来困难。同时,微能源系统中,热泵等能量转换设备的效率一般取为定值,未考虑热能传输过程对其的影响。因此,利用上述简化模型对微能源系统进行分析和优化,也会带来较大误差。文献[16-18]提出了一种热量流方法来描述换热器的传热过程,通过热电比拟,可将换热器热流比作电流,从而可应用普适的电学定律(如基尔霍夫定律)来构建热力系统整体约束,完整考虑传热过程的非线性约束。近年来,热量流法被广泛应用于制冷系统[19-20]、储能系统[21-23]、热电联产电厂中传热过程[24]以及超临界状态下热力系统[25]的分析与优化。
基于热力系统的热量流模型与电力系统的辐射网络潮流模型,本文针对微能源系统分别构建了热能与电能的传输约束,并结合光伏电池、太阳能集热器、储能电池、储热装置、空气源热泵及燃气锅炉建立了微能源系统中多能传输、转换与存储的整体模型。以系统投资与运行总成本最小为目标,以各装置出力与储能装置最佳容量为决策变量,构建了优化模型,并提出了以混合整数线性优化为基础的分层迭代优化策略,实现了系统的整体设计优化。最后,对比未完整考虑热量传输约束及其对能量转换设备效率影响的传统模型的计算结果,分析了热量传输特征对能量转换及存储特性的影响规律。
1 微能源系统的物理和数学模型
1.1 微能源系统的物理结构
本文考察应用于城市住宅小区的一个典型微能源系统,包含电力系统及热力系统。如图1所示,电力系统通过节点1与外界电网相连,节点2~6分别代表了小区内的建筑物1~5,各节点间有5条线路,距离如图中所示。每栋建筑物的电负荷包含建筑物内本身电负荷与电热泵装置用电,由光伏电池与外部传输的电能共同满足,同时,每栋建筑物配备储能电池进行调峰。
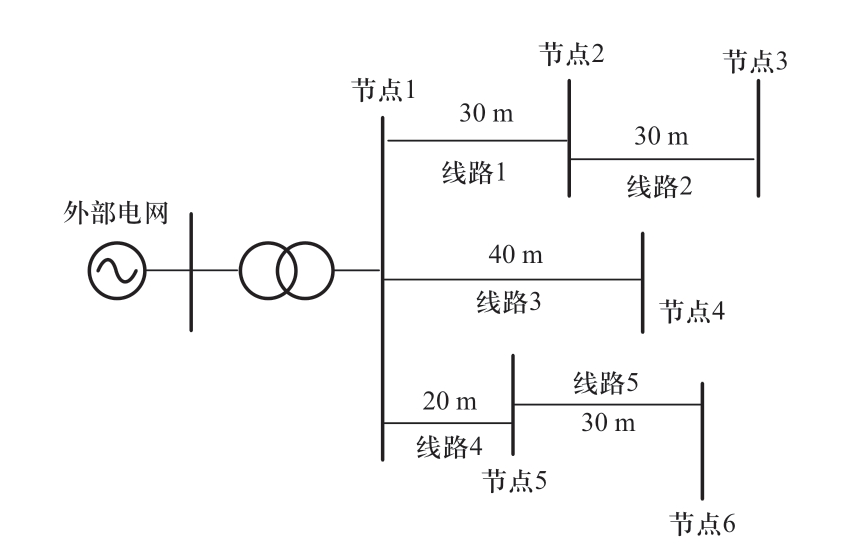
图1 电力系统拓扑图
Fig.1 Topology of power system
热力系统结构如图2所示,每栋建筑物的热力系统是独立的,不与小区内其他建筑物的供热网络相连。在每栋建筑物内,燃气锅炉消耗天然气,热泵消耗电能,储热装置储存来自太阳能集热器的热量共同进行供热。供热回水首先分为两股,分别流向燃气锅炉与热泵。其中,流经热泵的回水,一部分流入储热装置吸热后再与直接从热泵流出的热水混合,最后与从燃气锅炉流出的热水混合流入建筑物进行供热。
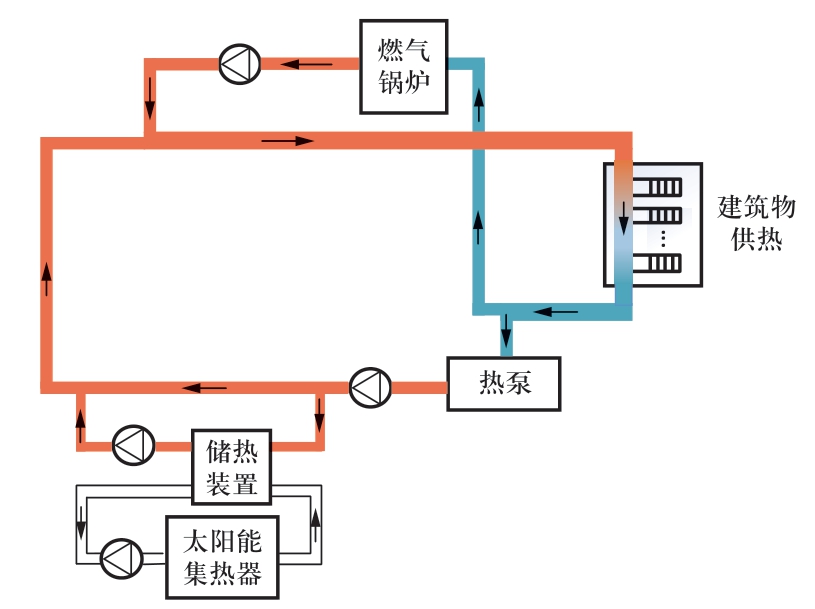
图2 热力系统结构图
Fig.2 Structure of thermal system
在该微能源系统中,电力系统与热力系统间的耦合元件为热泵装置,其消耗电能产生热能,并且热泵的性能系数(coefficient of performance,COP)受热能的传输特性、环境温度及制热量影响实时变化。
1.2 微能源系统的数学模型
1.2.1 电力系统传输约束
根据图1中的电力系统拓扑,与外界电网相连的节点1为松弛节点,节点2~6的注入有功Pinj,i与无功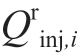 分别为:
分别为:
式中:Ppv与Qrpv分别为光伏电池产生的有功与无功;Pdis与Pchar分别为储能电池的放电与充电功率,由于电池容量较小,忽略其无功影响;Pload与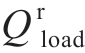 分别为负荷的有功与无功;Php与
分别为负荷的有功与无功;Php与 分别为热泵装置消耗的有功与无功;i代表了第i个节点。
分别为热泵装置消耗的有功与无功;i代表了第i个节点。
本文采取辐射型线路潮流计算模型,传输线路由一个等效阻抗模型代替。由于微能源系统中传输线路较短,相邻节点间电压的相角差可以忽略,则相邻节点i、j的电压有效值Ui、Uj间的关系为:
其中Rij与Xij分别为相邻节点i,j间线路的电阻和电抗。则该线路的传输损失ΔS为:
式中:Ploss与Qrloss分别为系统传输的有功和无功损失。整体电力系统的能量平衡方程为:
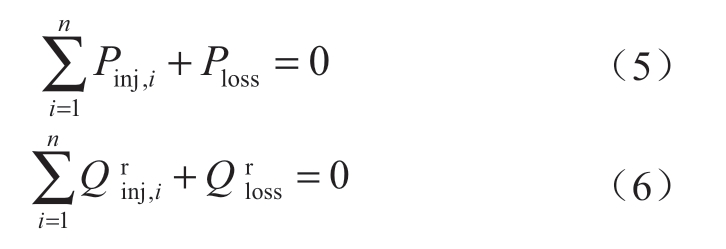
1.2.2 热力系统传输约束
由热量流法,单个逆流换热器的传热约束可表达为:
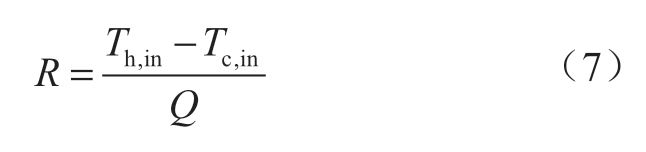
式中:Th,in和Tc,in分别为换热器热流体与冷流体的进口温度;Q为换热量;R为换热器热阻,其计算表达式为:
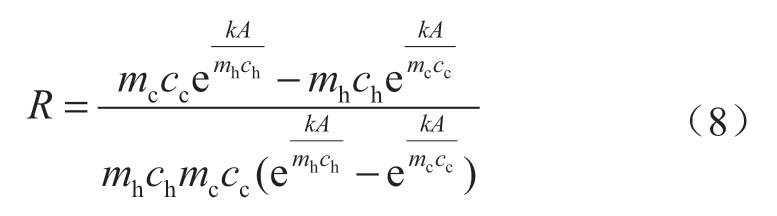
式中:mh和mc分别为换热器热流体与冷流体的质量流量;ch和cc分别为换热器热流体与冷流体的比热容;kA为换热器换热系数与换热器面积的乘积。换热器单侧流体经过换热后温度的变化可由一个附加热动势ε表示:
储热装置的储、放热过程可看作两个逆流换热器的换热过程,分别与从太阳能集热器流出的工质和供热管路工质进行换热。由于储热装置采用相变储热方式,可假设储热介质温度处于相变温度Tpc并保持不变,因此储、放热过程里储热装置侧工质的比热容可看作无限大。储热装置储、放热过程的热量流模型为:
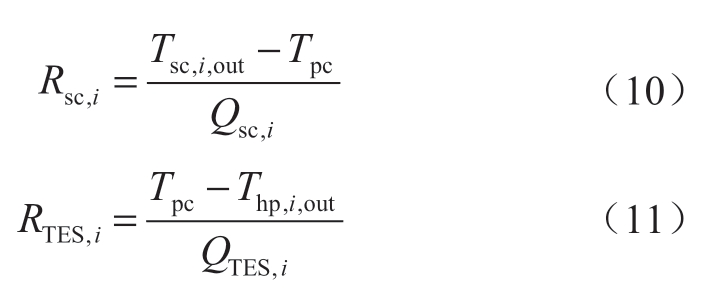
式中:Rsc与RTES分别为储热装置储、放热过程的热阻;Tsc,out与Thp,out分别为太阳能集热器与热泵装置的出口温度,即储热装置储、放热过程的外部流体进口温度。由于忽略漏热,太阳能集热器收集的热能Qsc,i即为储热装置输入的热能,QTES,i为从储热装置输出向供热支路的热量。热阻Rsc和RTES的表达式为:
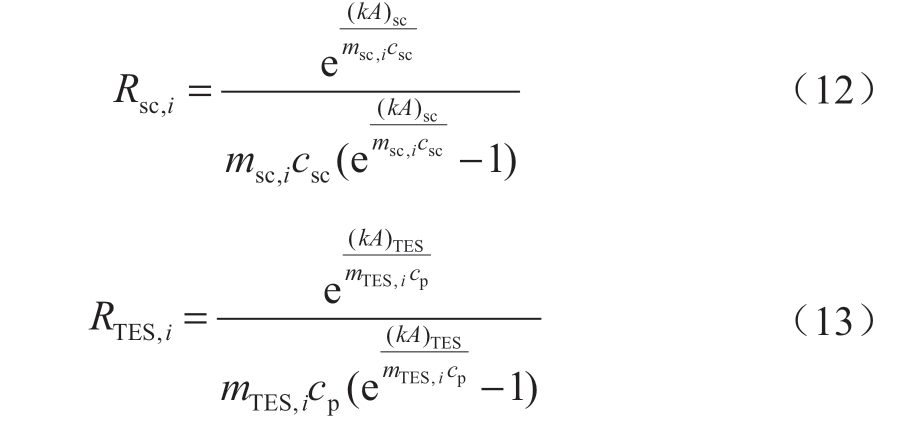
式中:msc和mTES分别为太阳能集热器回路工质与供热管路流入储热装置热水的质量流量;csc和cp分别为太阳能集热器回路工质与供热回路热水的比热容;(kA)sc和(kA)TES分别为储热装置储、放热过程的等效换热系数与换热面积的乘积。
储热装置的能量守恒方程为:
式中:MTES为储热装置中相变介质的质量;LTES为相变介质潜热;x为相变介质熔化的百分比,设定储热装置中介质始终处于相变状态:
储热装置中储存的热量在经历1个运行周期后应回归初值:
储热装置可看作是一个热容,由热量流法可比拟为一个电容。根据热量流法,储热装置的热量流模型如图3所示。
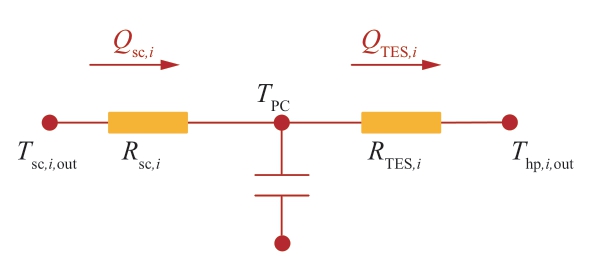
图3 储热装置热量流模型
Fig.3 Heat current model of TES device
供热热水流入建筑物开始供热,每栋楼换热的热量流模型为:
式中:Th,i,in为换热器进口温度;Tb为建筑物室内温度。换热过程的热阻Rh,i为:
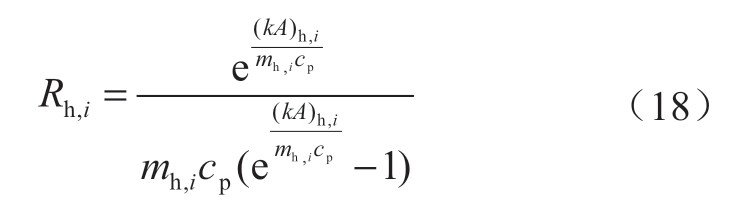
式中:mh,i为建筑物内供热送水的质量流量;(kA)h,i为各栋换热器换热过程的等效换热系数与换热面积的乘积。图4给出了建筑物i内供热过程的热量流模型。
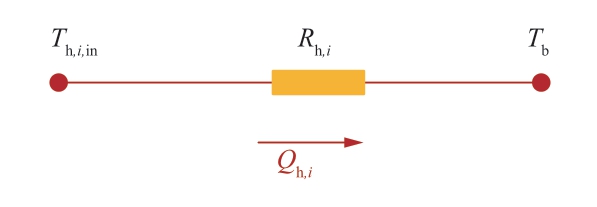
图4 建筑物i供热过程热量流模型
Fig.4 Heat current model of supply network in Buildingi
热泵装置与燃气锅炉也向供热支路提供热量,分别用电流源Qhp,i和Qgb,i来表示。图5给出了建筑物i整个热力系统的热量流模型,图中附加热动势εhp-TES,i代表了从储热装置出来的热水与直接从热泵流出的热水混合后的温度变化,εhp-gb,i代表了从储热装置与热泵流出的热水再与从燃气锅炉流出的热水混合后的温度变化。εhp-TES,i和εhp-gb,i分别为:
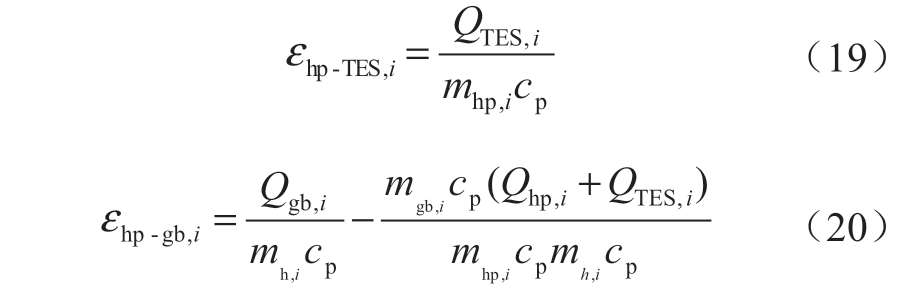
式中:mhp,i和mgb,i分别为流经热泵与燃气锅炉热水的质量流量;Qhp,i和Qgb,i分别为热泵和燃气锅炉产生的热功率。图5中Thp-TES,i代表了从储热装置出来的热水与直接从热泵流出的热水混合后的温度。
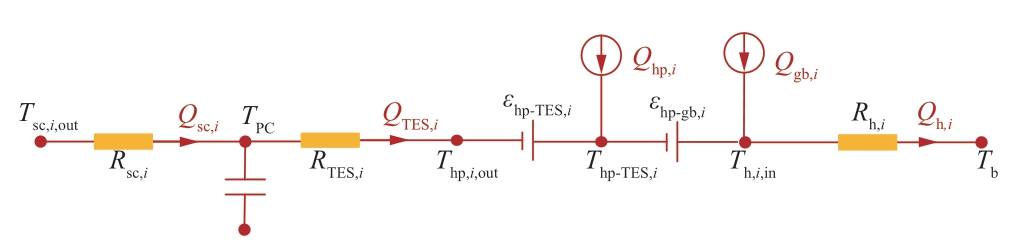
图5 建筑物i热力系统的热量流模型
Fig.5 Heat current model of thermal system in Buildingi
由热量流模型可写出热力系统的约束方程为:
由热量流法建立热力系统的约束方程,能从热量输运的视角构建整体系统约束,并且完整地考虑传热约束的非线性。
本文考虑每栋建筑物内的热力网络是独立的,建筑物间并未有供热管道相连,所以供热管道长度较短,则伴随着管道中的流体流动引起的热量输运过程中的漏热与其过程的延迟特性可忽略。热力系统的热平衡方程为:
同时,根据热力系统结构,各质量流量也存在相关约束:

1.2.3 光伏电池
光伏电池产电量受光伏电池温度与辐射强度影响较大,因此文献[26]提出了一种模型来模拟光伏电池的产电量,该模型采用了5个参数来代表环境对光伏电池造成的非线性影响。其中,单个光伏模块的产电量为:
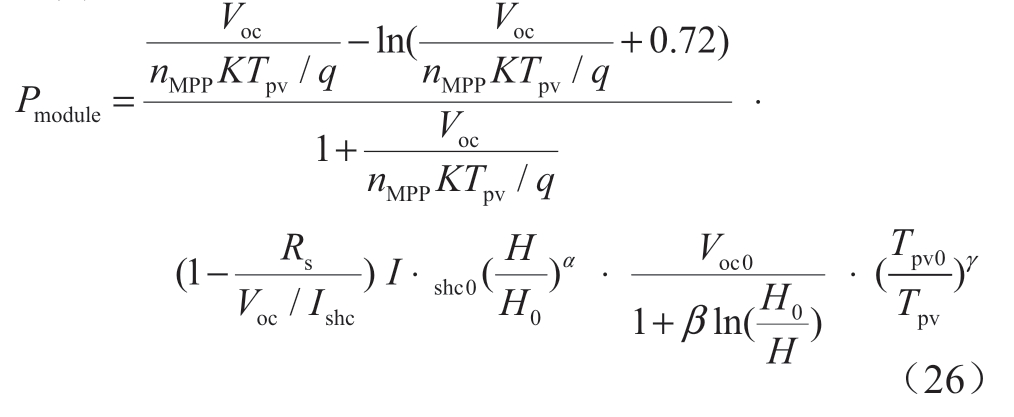
式中:H0和Tpv0分别为标准状态下太阳辐射和光伏电池温度;H和Tpv分别为实际太阳辐射和光伏电池温度;Ishc0和Ishc分别为在标准状态和实际情形下的短路电流;Voc0和Voc分别为在标准状态和实际情形下的开路电压;α、β、γ、Rs和nMPP是关于光伏电池的5个参数,α与决定光电流的非线性因素相关,β与光伏电池的具体设计参数有关,γ考虑了温度与电压之间的非线性影响,Rs是串联电阻,nMPP表示了最大功率点的理想程度;q为库伦电荷;K为玻尔茨曼常数。
将光伏电池模块有序连接起来形成光伏阵列,光伏装置总功率为:
式中:Np和Ns是光伏电池并联和串联的个数;ηMPPT代表了最大功率的效率。光伏电池产生电能经由逆变器转换为交流,其中电能损失用效率来表示,实际光伏装置的产电量为:
其中μinv是逆变器的效率。由于规模较小电压较低,光伏装置在电网中认为具有恒定功率因数。
1.2.4 储能电池
储能电池的能量守恒方程为:
式中:E为电池中储存的能量;Pchar和Pdis分别为电池充放电功率;ηBAT为充放电过程的效率;k代表时间节点k。考虑其充放电深度约束:
式中:SOC,max和SOC,min分别为储能电池充放电深度上、下限。电池装置容量为Emax,电池状态SOC为:
传输功率也有极限PBAT,max,其传输功率极限定为电池容量的1/3:
同储热装置,当经历1个运行周期后,电池中储存的能量应该回归到初态,其传输功率极限定为电池容量的0.3倍:
1.2.5 燃气锅炉
燃气锅炉消耗天然气进行供热,其热出力为:
式中:ηgb为燃气锅炉的效率;qgas为天然气热值;Bi,gas为天然气的消耗速率。燃气装置的能量守恒方程为:
式中:Tgb,i,in和Tgb,i,out分别为燃气锅炉的进、出口温度。燃气锅炉热出力存在上限Qgb,i,max:
1.2.6 太阳能集热器
太阳能集热器收集的热能Qsc,i为:
式中:ηsc,i为太阳能集热器的效率;Asc为集热器面积;H为太阳辐射。太阳能集热器效率ηsc,i受集热器进口温度、环境温度和太阳辐射影响,本文采用一种模型考虑其效率随热量输运的影响[27]:

式中:Tsc,i,in为集热器工质进口温度;Tair为环境温度。太阳能集热器能量守恒方程为:
1.2.7 热泵装置
热泵装置为电力系统与热力系统间的耦合装置,其热出力Qhp,i,k与耗电量Php,i,k之间的关系为:
式中:ηhp为热泵的COP,受热泵出口温度Thp,out和环境温度Tair的影响,具体关系式见附录A。热泵装置功率也存在限制:
2 系统优化模型及求解策略
微能源系统中电力网络与热力网络给定,热泵装置、燃气锅炉、光伏装置及太阳能集热器的容量大小给定,为满足一定的电负荷与热负荷,对各装置出力进行运行优化,同时,对储能装置的最佳容量进行规划。因此,系统的优化目标为包含运行成本与储能装置成本的总成本:
式中:Cgas为微能源系统运行过程中燃气锅炉消耗天然气总成本;Cgridin为系统运行周期内从外部电网总的购电成本;CBAT为折算到运行周期内的电池总安装与运维成本;CTES为折算到运行周期内的储热装置总安装与运维成本。
以运行周期内各装置实际出力与储能装置的容量为决策变量,第1章建立的微能源系统约束为优化约束,式(42)为优化目标建立系统优化模型。由于电力系统与热力系统的传输约束具有非线性,系统优化模型为非线性模型,且同时包含运行优化与装置规模优化,经历1个运行周期,变量数量较大,采取一般非线性优化方法如遗传算法等耗时较长,甚至不能得出结果。
本文将非线性优化问题拆分成线性优化问题与非线性方程组求解问题的集合,反复迭代得到合理最优结果。优化计算分为3层,首先内层为一个混合整数线性优化(MILP)问题,考虑微能源系统中的功率平衡与各装置出力上下限等约束,对系统运行过程中的电力系统与热力系统各功率(Php,Pchar,Pdis,Pgrid,Qhp,Qgb,QTES……)与储能装置规模进行优化。该层优化里,电力系统传输网损与热泵的COP为定值。
接下来计算电力系统潮流约束。通过配电网辐射型网络潮流迭代计算得到各处电压与潮流。进行潮流计算后,可得出系统的网损,将网损代回内层的混合整数线性优化中的功率平衡方程,可重新优化计算系统的各功率。再由新的注入功率得到新的潮流分布,以及新的网损,形成迭代,直至收敛。
最后考虑热力系统传热约束,通过对传热方程进行求解可算得各部分流量与各节点温度。由热泵出口温度和环境温度可得到热泵的COP,并且可以得到由传输约束计算得来的装置出力约束,如储热装置储、放热功率最大值等,将新算得热泵COP与装置出力极限带入内层的混合整数线性优化,算得新的系统各功率,进行迭代并使得上层潮流计算收敛,再重新解传热方程得到更新的COP,重复迭代计算最终整体收敛。优化计算使用MATLAB软件及Cplex工具箱,高效实现系统运行模拟与装置规模优化。
3 优化结果及分析
图6给出了微能源系统中各建筑物一天内的电负荷与热负荷。图7给出了一天内的太阳辐射强度。系统从外部电网购电存在分时电价,一共分为3种时段:低谷时段(0:00—7:00,23:00—24:00),电价为 0.058 4美元/kWh;平时段(7:00—9:00,21:00—23:00),电价为0.102 2美元/kWh;高峰时段(9:00—21:00),电价为0.131 4美元/kWh。优化计算中用到的电力系统参数、热力系统参数分别如表1与表2所示。天然气的热值为9.88 kWh/m3,燃气锅炉的最大出力功率为45 kW,天然气的价格为0.35美元/m3。设定需要规划的每栋建筑物储能装置的规模相同,储能装置的正常使用年限为20年。
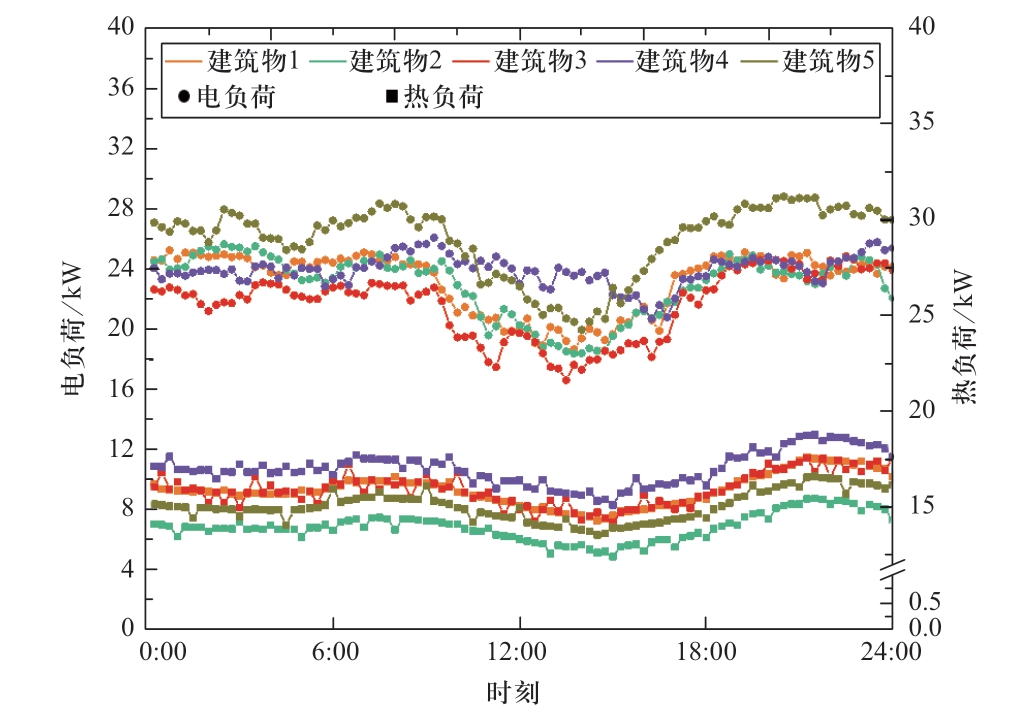
图6 系统各建筑物一天内电负荷和热负荷
Fig.6 Electric load and heating load of each building in a day
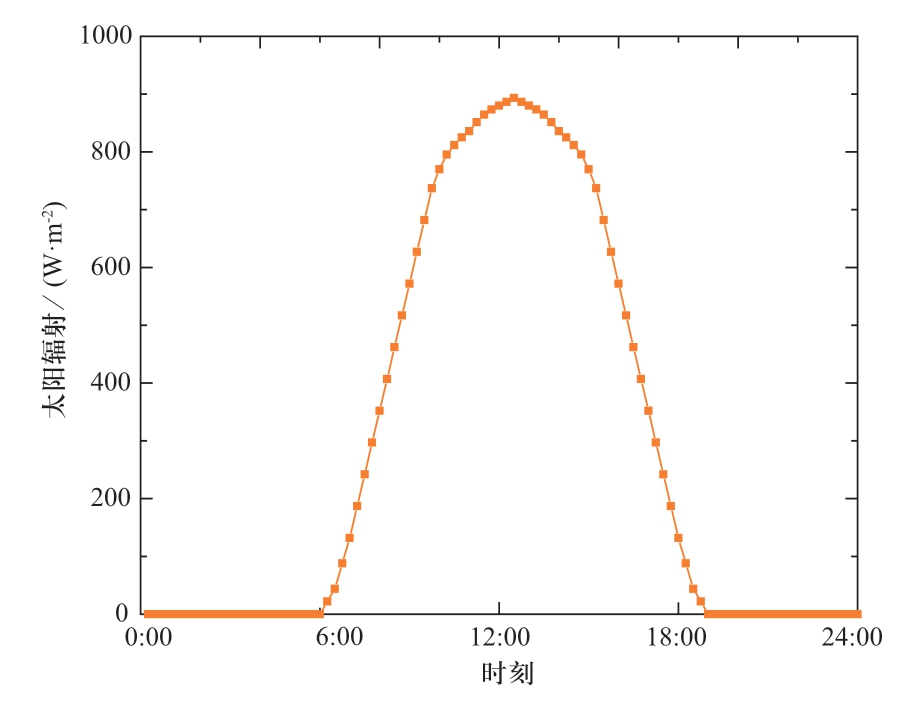
图7 一天内太阳辐射强度
Fig.7 Solar irradiation in a day
表1 电力系统参数设置
Table1 Parameter settings of power system
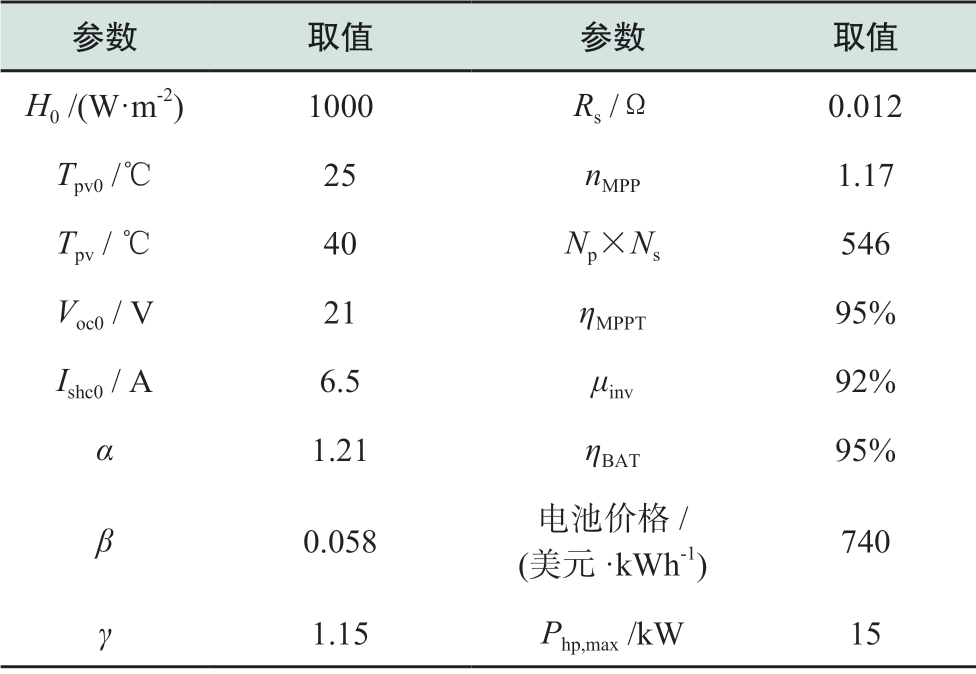
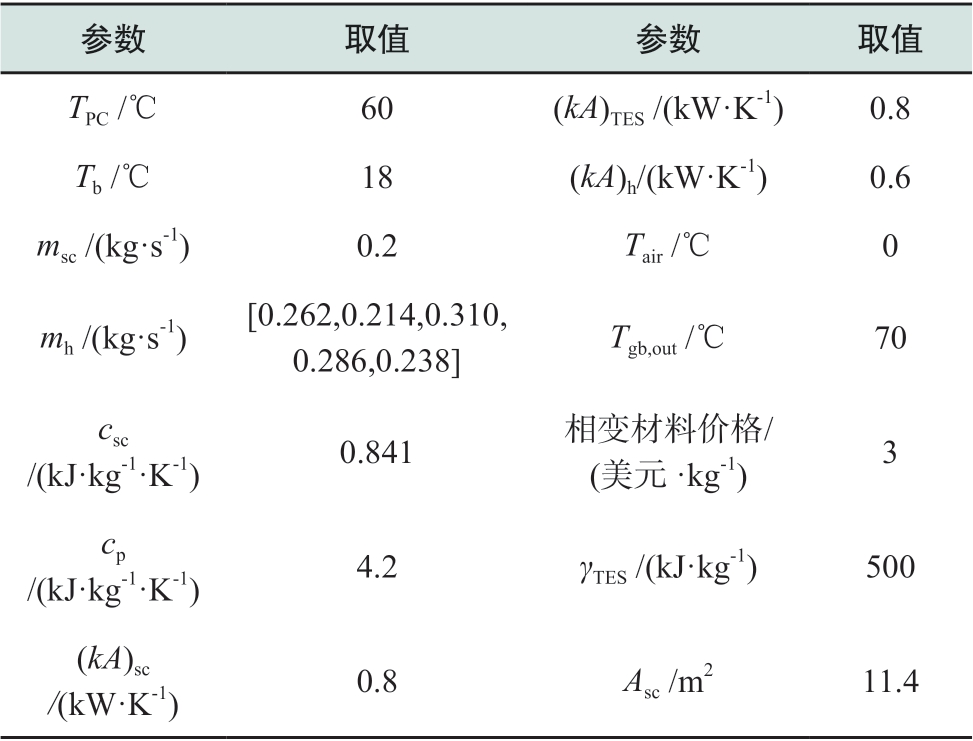
表2 热力系统参数设置
Table2 Parameter settings of thermal system
本文比较两个微能源系统整体模型下系统的运行模拟及装置规模优化结果。模型Ⅰ为本文第1、2章中建立的模型,考虑了电力系统和热力系统的非线性传输约束。模型Ⅱ则不考虑热力系统传输约束,仅考虑各部件热出力等于热负荷,即热力系统功率平衡。由于热泵COP与太阳能集热器效率受温度的影响会发生变化,而模型Ⅱ中不涉及热力系统各处工质温度,所以模型Ⅱ不能考虑热量传输对能源转换装置的影响,即热泵与太阳能集热器能量转换效率的变化。模型Ⅱ中热泵COP取为定值2.602,太阳能集热器效率同样取为定值0.38,均为模型I中热泵COP与太阳能集热器效率在一天工作时段内的平均值。其余部分模型Ⅰ与模型Ⅱ相同。
3.1 热量传输对于能量转换特性的影响
热泵COP受热泵出口水温和外界环境温度影响,太阳能集热器效率受集热器出口工质温度与环境温度影响。热力系统热量输运造成的系统各处工质温度变化会对两种设备的效率产生影响。图8给出了模型Ⅰ中建筑物1内热泵COP与太阳能集热器效率在一天中的变化情形。热泵出口水温随热负荷变化及各供热装置出力变化实时波动,热泵COP也是波动的。热泵COP总体呈现与热泵出力负相关的趋势,这与流经热泵的供热回水质量流量有关。比如,对于如图2的热力系统,流向热泵的供热回水其中一部分还会流向储热装置吸热,当热泵出力较小,而储热装置承担了一部分热负荷时,流经热泵的热水质量流量仍然较高,则以较小功率加热较大流量的水,热泵出口温度较低,因此COP就会较高。太阳能集热器效率则呈现先增大后减小的趋势,主要原因是太阳辐射强度在一天内先增大后减小。其中,热泵和太阳能集热器未工作时效率用虚线连接(不具备物理含义)。由于太阳能集热器效率变化剧烈,计算其一天内设备总出力,模型Ⅰ中太阳能集热器出力为38.40 kWh,而模型Ⅱ中太阳能集热器出力仅为30.78 kWh,为模型Ⅰ中的80.2%。由于模型Ⅱ不能准确描述太阳能集热器效率的变化,当一天中辐射较强时,太阳能集热器的效率也较高,则太阳能集热器吸收的热量就会更多,单纯取一天效率的平均值不能准确反映太阳能集热器的吸热量。
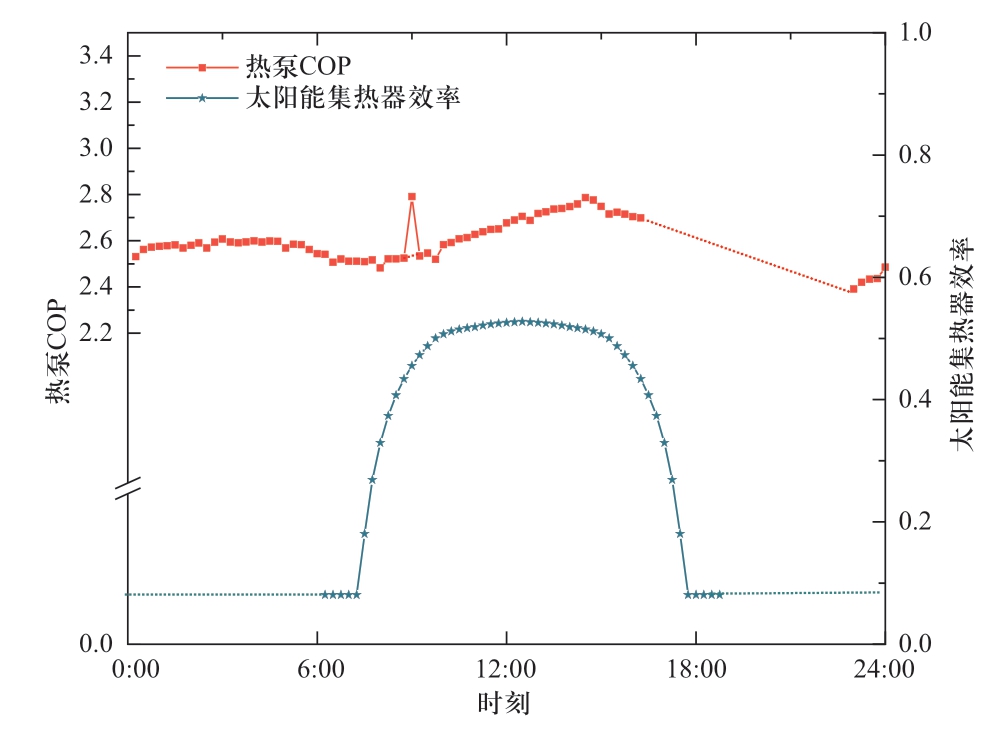
图8 模型I下热泵与太阳能集热器效率的变化
Fig.8 COP of heat pump and efficiency of solar collector in Building 1 during the day in model I
3.2 热量传输对于能量存储装置容量的影响
图9给出了两种模型优化后储能电池和储热装置的最佳容量。可以看出,两种模型下电池的最佳容量相近,而模型Ⅱ中储热装置的容量远小于模型Ⅰ中结果。模型Ⅱ中储热装置的容量约为模型Ⅰ中的48.9%。这是由于储热装置储存太阳能集热器产生的热能,而模型Ⅱ中太阳能集热器在一天内产生的总热量较低,且由于太阳能集热器效率为定值,其产生热量的速率也较模型Ⅰ中均匀,模型Ⅰ中随着时间从早晨到正午,太阳能集热器产热量急剧增加,需要更大容量的储热装置。
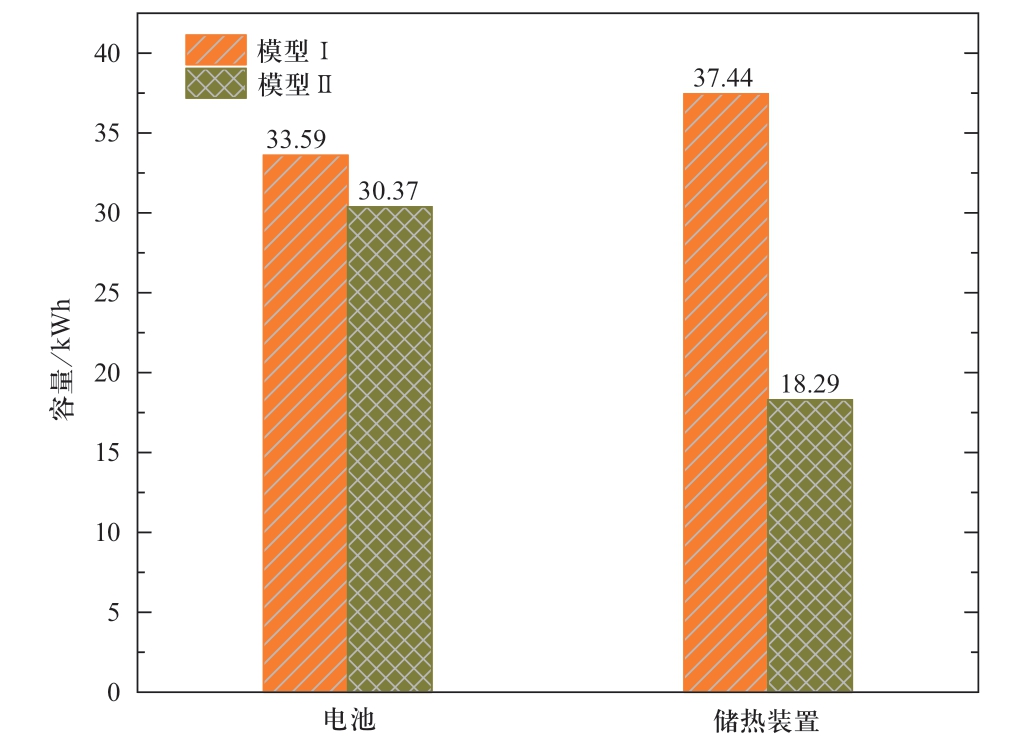
图9 两种模型下建筑物1中储能装置最佳容量
Fig.9 Optimal capacities of energy storage devices in Building 1 of two models
图10给出了两种模型下电池和储热装置的实时储存能量。两种模型下结果的变化趋势相同,电池装置储电量有2个峰值,首先由于凌晨时刻电价较低,电池储存电量。电价上升到平时段电价后,电池逐渐放电减少向电网买电以节省运行成本。第2个峰值是由于白天太阳辐射增强,光伏电池出力逐渐增加以至超出负荷,多余电能储存起来备用。


图10 两种模型下建筑物1中储能装置储存能量变化
Fig.10 Energy stored in energy storage devices in Building 1 of two models
储热装置储存太阳能集热器的能量,存在1个峰值。由于凌晨电价较低,由热泵出力满足热负荷,当电价上升时,储热装置储热量降低,来代替部分热泵出力。当电价再上升到达高峰电价时,热泵供热成本超过燃气锅炉,此时供热热量主要由燃气锅炉和储热装置提供,储热装置储热量逐渐减少。
两种模型下储能装置的最大容量决定了模型Ⅱ中电池储存的能量较模型Ⅰ略低,模型Ⅱ中储热装置储存的能量远低于模型Ⅰ中储存能量。
3.3 系统运行结果对比
模型Ⅰ与模型Ⅱ中热泵、燃气锅炉和储热装置 3种供热设备的热出力如图11所示。两种模型下装置运行趋势相同,热泵在晚间电价高峰时不提供热量,由燃气锅炉和储热装置进行供热。由于分时电价政策影响,在电价峰值时热泵供热是比燃气锅炉供热更不经济的,但是因为有光伏出力与电池等可以供给一部分电能给热泵,热泵在电价峰值时大部分时间仍然开机供热。当这部分电能耗尽后需要从外部电网购入电能时,系统使用燃气锅炉和储热装置进行供热。但是由于太阳能集热器总产热量在模型Ⅰ下比模型Ⅱ更大,所以图11(a)中储热装置总放热量比图11(b)大,而图11(a)中热泵总出力比图11(b)小。
图12给出了2种模型下微能源系统从外部电网买入的电量。由于2种模型的电力系统部分模型相同,从外部购电结果较为类似。受分时电价影响,电价峰值时尽可能不购入电能,电价处于低谷时(如凌晨)大量购入电能进行存储。

图11 两种模型建筑物1中各供热设备出力情形
Fig.11 Thermal powers in Building 1 of two models
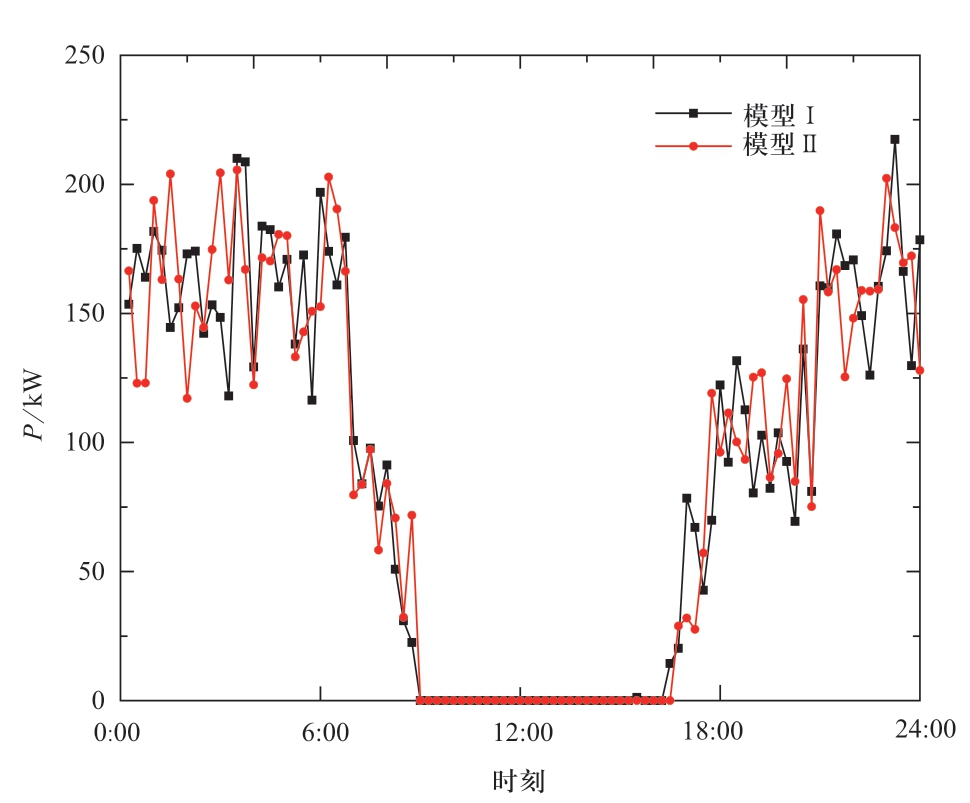
图12 两种模型一天内微能源系统从外界购入的电能
Fig.12 Powers purchased from public grid of two models
图13给出了由模型Ⅰ得出的微能源系统中各传输线路一天内有功功率的变化。系统各传输线路编号如图1所示,图1中从右向左传输认为线路传输功率为正。可看出一天中夜晚时段均为功率从左向右传输,即从外部电网输入电能,与图12中结果一致。日中时段线路传输功率有正有负,表明微能源系统自给自足,不从外界输入电能,能量在各建筑物间流动。相应地,图14给出了模型Ⅰ下各建筑物节点(即节点2~6)电压有效值在一天中的变化情况。节点1为微能源系统与外部电网连接节点,电压有效值设定为1。
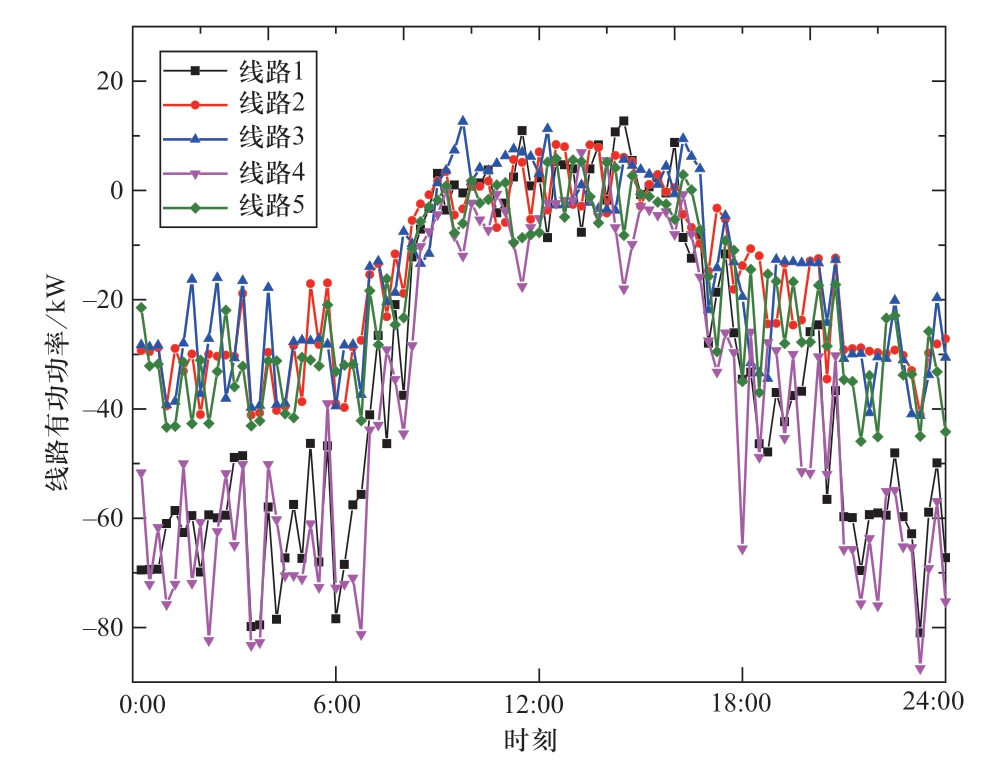
图13 模型Ⅰ一天内系统传输线路有功功率变化
Fig.13 Active powers of transmission lines during a day of model I

图14 模型Ⅰ一天内系统各节点电压有效值变化
Fig.14 Voltage variations of each bus during a day of model I
4 结论
基于热力系统热量流模型与辐射网络潮流模型,本文构建了微能源系统中热量与电量的完整非线性传输约束,并考虑了热量传输与转换之间的相互影响。结合光伏电池、太阳能集热器、储能电池、储热装置、空气源热泵及燃气锅炉,建立了微能源系统的整体数学模型。以运行周期内各装置实际出力与储能装置的容量为决策变量,以系统投资和运行总成本最小为优化目标,构建了系统优化模型。
针对上述非线性优化问题,本文提出了一种分层迭代优化策略,对微能源系统进行了整体设计优化。内层利用混合整数线性优化方法对系统运行过程中的各装置出力与储能装置规模进行优化;外两层依次考虑潮流约束与传热约束,可得到各处电压、潮流与节点温度、支路流量等,迭代更新热泵COP与电力系统传输网损等。
通过与未考虑热量传输约束的传统模型对比,发现热量输运对能量转换效率与储能装置容量影响较大。未考虑热量传输对热泵和太阳能集热器效率的影响时,太阳能集热器总出力为考虑热量输传输影响的80.2%,储热装置最佳容量差异明显,仅为考虑热量输传输影响的48.9%。
在微能源系统中,不同形式能量的物理属性和传输特性差异较大,现有模型在研究多能流的传输和转换过程时,一般情况对能量的传输过程,特别是热量传输过程作一定程度的简化,难以完整考虑热量传输约束及其对能量转换的影响。本文构建了热力系统中完整的非线性热量传输模型,并考虑了热量传输对热泵等电-热转换装置能量转换效率之间的影响。计算结果表明:当考虑热量传输约束及其对能量转换的影响时,系统的运行方式以及装置容量的优化结果与未考虑热量传输约束的情形差异较大,说明微能源系统相关研究及工程实际问题中需要考量能量的传输约束,而不仅仅是考虑功率平衡。同时,本文提出的分层迭代优化策略也为综合能源系统优化问题提供了一种可行思路。
参考文献
[1] CHU S,MAJUMDAR A.Opportunities and challenges for a sustainable energy future[J].Nature,2012,488(7411): 294-303.
[2] LUND H.Renewable energy strategies for sustainable development[J].Energy,2007,32(6): 912-919.
[3] PAN Z G,GUO Q L,SUN H B.Interactions of district electricity and heating systems considering time-scale characteristics based on quasi-steady multi-energy flow[J].Applied Energy,2016,167: 230-243.
[4] MANCARELLA P.MES(multi-energy systems): an overview of concepts and evaluation models[J].Energy,2014,65: 1-17.
[5] JIN X L,WANG X D,MU Y F,et al.Optimal scheduling approach for a combined cooling,heating and power building microgrid considering virtual storage system[C]//2016 IEEE Power and Energy Society General Meeting(PESGM),July 17-21,2016.Boston,MA,USA.IEEE,2016.
[6] 徐宪东.电/气/热微型能源系统的建模、仿真与能量管理研究[D].天津:天津大学,2014.
XU Xiandong.Modelling,simulation,and energy management research for electricity,gas,and heat based micro energy system[D].Tianjin: Tianjin University,2014(in Chinese).
[7] 刘小军,李进,曲勇,等.冷热电三联供(CCHP)分布式能源系统建模综述[J].电网与清洁能源,2012,28(7):63-68.
LIU Xiaojun,LI Jin,QU Yong,et al.Overview of modeling of combined cooling heating and power system[J].Power System and Clean Energy,2012,28(7): 63-68(in Chinese).
[8] 宋阳阳,王艳松,衣京波.计及需求侧响应和热/电耦合的微网能源优化规划[J].电网技术,2018,42(11):3469-3476.
SONG Yangyang,WANG Yansong,YI Jingbo.Microgrid energy source optimization planning considering demand side response and thermo-electrical coupling[J].Power System Technology,2018,42(11): 3469-3476(in Chinese).
[9] GEIDL M,ANDERSSON G.Optimal power flow of multiple energy carriers[J].IEEE Transactions on Power Systems,2007,22(1): 145-155.
[10] GEIDL M,KOEPPEL G,FAVRE-PERROD P,et al.Energy hubs for the future[J].IEEE Power and Energy Magazine,2007,5(1): 24-30.
[11] MA T F,WU J Y,HAO L L.Energy flow modeling and optimal operation analysis of the micro energy grid based on energy hub[J].Energy Conversion and Management,2017,133: 292-306.
[12] HANDANI Z B,HASHIM H,ALWI S R W,et al.A mixed integer linear programming(MILP)model for optimal design of water network[C]//2011 Fourth International Conference on Modeling,Simulation and Applied Optimization,April 19-21,2011.Kuala Lumpur,Malaysia.IEEE,2011.
[13] WOUTERS C,FRAGA E S,JAMES A M.An energy integrated,multi-microgrid,MILP(mixed-integer linear programming)approach for residential distributed energy system planning - A South Australian case-study[J].Energy,2015,85: 30-44.
[14] CALVILLO C F,SÁNCHEZ-MIRALLES A,VILLAR J.Assessing low voltage network constraints in distributed energy resources planning[J].Energy,2015,84: 783-793.
[15] JIANG X S,JING Z X,LI Y Z,et al.Modelling and operation optimization of an integrated energy based direct district waterheating system[J].Energy,2014,64: 375-388.
[16] CHEN Q.Entransy dissipation-based thermal resistance method for heat exchanger performance design and optimization[J].International Journal of Heat and Mass Transfer,2013,60: 156-162.
[17] CHEN Q,FU R H,XU Y C.Electrical circuit analogy for heat transfer analysis and optimization in heat exchanger networks[J].Applied Energy,2015,139: 81-92.
[18] CHEN Q,HAO J H,ZHAO T.An alternative energy flow model for analysis and optimization of heat transfer systems[J].International Journal of Heat and Mass Transfer,2017,108: 712-720.
[19] HAO J H,CHEN Q,XU Y C.A global optimization method for regenerative air refrigeration systems[J].Applied Thermal Engineering,2014,65(1/2): 255-261.
[20] CHEN Q,XU Y C,HAO J H.An optimization method for gas refrigeration cycle based on the combination of both thermodynamics and entransy theory[J].Applied Energy,2014,113: 982-989.
[21] CHEN Q,ZHAO T.Heat recovery and storage installation in large-scale battery systems for effective integration of renewable energy sources into power systems[J].Applied Thermal Engineering,2017,122: 194-203.
[22] ZHAO T,MIN Y,CHEN Q,et al.Electrical circuit analogy for analysis and optimization of absorption energy storage systems[J].Energy,2016,104: 171-183.
[23] HU K,CHEN L,CHEN Q,et al.Phase-change heat storage installation in combined heat and power plants for integration of renewable energy sources into power system[J].Energy,2017,124: 640-651.
[24] DAI Y,CHEN L,MIN Y,et al.Dispatch model of combined heat and power plant considering heat transfer process[J].IEEE Transactions on Sustainable Energy,2017,8(3): 1225-1236.
[25] CHEN Q,ZHAO S Y,CHEN X,et al.The power flow topology of heat transfer systems at supercritical conditions for performance analysis and optimization[J].International Journal of Heat and Mass Transfer,2018,118: 316-326.
[26] ZHOU W,YANG H X,FANG Z H.A novel model for photovoltaic array performance prediction[J].Applied Energy,2007,84(12): 1187-1198.
[27] SAID S A M,EL-SHAARAWI M A I,SIDDIQUI M U.Analysis of a solar powered absorption system[J].Energy Conversion and Management,2015,97: 243-252.
附录A 热泵COP随热泵出口温度与环境温度的变化关系
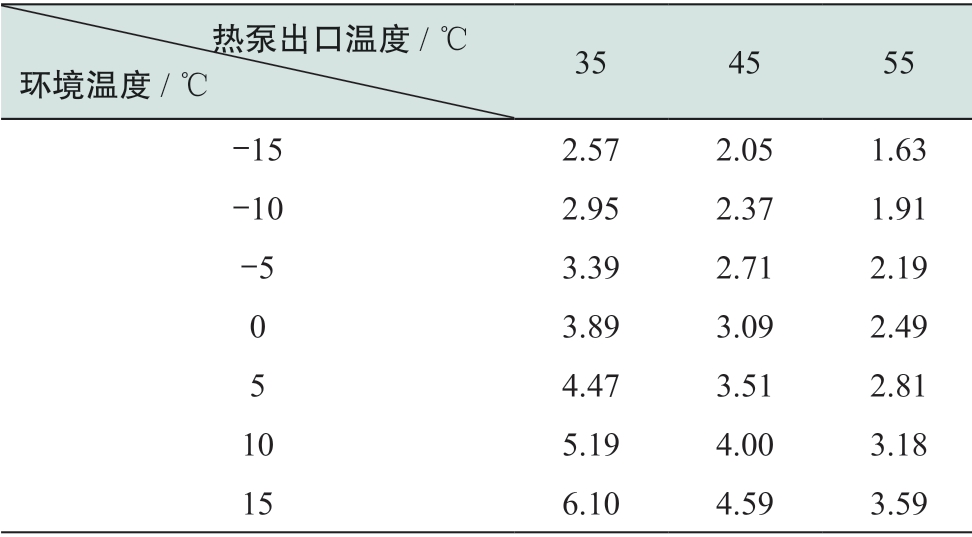
表A1为热泵采用R22制冷剂时COP随热泵出口温度与环境温度的变化情况。对表中数据进行拟合后,可得到COP关于热泵出口温度与环境温度的变化式为:
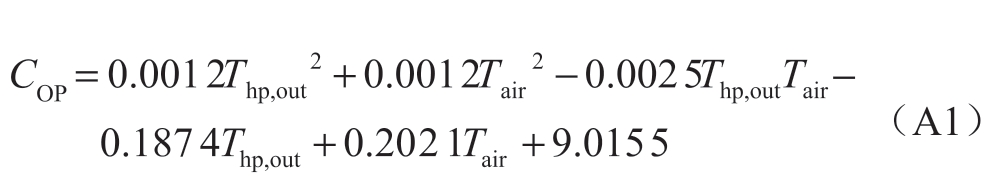
式中:Thp,out和Tair分别为热泵装置的出口温度与环境温度。
表A1 不同热泵出口温度与环境温度下热泵COP变化情况
TableA1 COPs under different outlet temperatures and environment temperatures
Influence Mechanism of Multi-energy Transport,Storage,and Conversion Processes in Micro-energy System
GOU Xing1,CHEN Qun1,2*,SUN Yong3,MA Huan1,HE Kelun1,LI Zhenyuan3
(1.Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,Department of Engineering Mechanics,Tsinghua University,Haidian District,Beijing 100084,China;2.State Key Lab of Control and Simulation of Power Systems and Generation Equipments,Department of Electrical Engineering,Tsinghua University,Haidian District,Beijing 100084,China;3.State Grid Jilin Electric Power Supply Company,Changchun 130000,Jilin Province,China)
Abstract: A micro-energy system integrates electric power,thermal energy,and natural gas,which is effective for energy conservation,by considering the complementary characteristics of multi-energy conversion,storage,and transmission processes.However,the physical properties and transmission characteristics of different energy types in a microenergy system are distinct.The existing models of microenergy systems do not consider heat transfer constraints and their influences on energy conversion processes.This work constructs nonlinear heat transfer constraints in a thermal system and considers their effect on energy conversion processes for multi-energy management in micro-energy systems.A photovoltaic device,battery,heat pump,gas boiler,solar collector,and thermal storage device are combined to build the overall optimization model of a micro-energy system with the objective of minimizing the total cost including fixed investment and operating cost.Then,we propose a hierarchical iterative strategy with mixed integer linear optimization,and the influences of heat transfer,energy conversion,and energy storage processes in micro-energy system are examined.If the heat transfer constraints of the thermal system and their effects on the efficiencies of the heat pump and solar collector are not considered,the total heat generation of the solar collector is 80.2% and the optimal capacity of the thermal storage device is only 48.9% compared to when the heat transfer constraints and their effects are considered.
Keywords: micro-energy system; multi-energy transport; energy conversion; energy storage; heat transfer constraints
作者简介:

苟星
苟星(1994),女,博士研究生,研究方向为综合能源系统的运行模拟及规划,E-mail:goux16@mails.tsinghua.edu.cn。
陈群(1981),男,教授,研究方向为热力系统优化、综合能源系统的运行模拟及规划等。通信作者,E-mail:chenqun@tsinghua.edu.cn。
马欢(1995),男,博士研究生,研究方向为综合能源系统的运行模拟及优化等,E-mail:mh17@mails.tsinghua.edu.cn
(责任编辑 李锡)
