0 引言
随着厂网分开的实行及电力市场的发展,发电公司成为独立经济实体。发电机组检修计划的制定主体有望由系统运行部门转变为发电公司[1]。
美国宾夕法尼亚、新泽西和马里兰3州互联系统(Pennsylvania-New Jersey-Maryland,PJM)[2]、北欧和英国[3]等电力市场都允许在一定前提下由发电公司自主确定发电机组的检修计划。但澳大利亚电力市场曾发生过发电公司在高峰负荷时期对大容量机组进行检修的情况[4];美国加州于2000年发生发电公司依靠检修实现发电容量持留,导致电力紧缺的情形[5]。此时,发电公司的检修计划需要满足非检修时段利益的最大化,该利益与市场规则相关。
中国电力市场尚处发展初期,调度机构仍然占有集中确定机组检修计划的权力。中长期合约交易电量占整个电力交易的70%~80%,有必要针对中长期合同竞价市场规则[6],模拟发电公司自主确定机组检修计划时的检修行为,分析其对系统运行可能造成的影响,从而为是否放开以及如何放开检修计划安排奠定基础。大用户直接交易是合约交易的组成部分[7],但与双边磋商有关,涉及随机因素较多,不在本文讨论范围内。
已有不少工作分析了市场环境下的检修计划安排,其中一部分工作仍是基于集中优化的框架,市场在模型中主要通过优化目标来实现,如文献[8-9]构建了包含检修费用与损失发电费用的优化目标。但这部分工作难以体现发电公司间制定决策的相互影响。另一部分工作则是引入了博弈论以分析发电公司的检修行为,可以反映多主体分散决策的特点。但绝大部分文献直接给定电价预测信息[10-11]或根据确定的函数关系求解每一时段电价[3,12],不能体现电力市场的电价出清规则;有少量文献考虑了电价出清,但都假设机组总是以边际发电成本参与竞价[13-14],难以反映发电公司可能的抬升市场出清电价行为与检修行为的关联。因而,本文构建综合机组竞价和检修策略制定的博弈论模型,既能反映发电公司间检修安排的博弈,又能体现发电公司在中长期合同竞价市场中的竞价过程。
本文结合中国中长期合同竞价市场的基本规则,在机组检修由发电公司自主确定的假设下,基于综合机组竞价和检修策略制定的博弈论分析方法,分析中长期合同竞价市场下机组的竞价行为和检修行为,探讨其对系统运行的影响。
1 中长期合同竞价市场的基本规则
中长期合同竞价市场交易的基本规则是:交易机构首先公布计划周期(一般为年或月)内的竞争电量和竞价上限,之后各个交易主体申报计划周期内能够提供的电量以及电量对应的期望价格。按报价排序结果,电网从报价最低的发电公司起依次调用,确定各发电公司直至调用的总发电量与竞争电量平衡,最终以被调用的最后一个发电公司的竞价作为统一的市场边际价格进行结算,即合约电价[15]。
本文不考虑发电公司预留发电容量用以现货市场竞争的因素,认为机组按其全部发电量作为参与中长期市场竞争的电量,因而竞价信息是竞价行为的分析内容。
2 综合机组竞价和检修策略的博弈论方法
考虑机组在中长期合同竞价市场中的竞价以及相应收益,本文采取两阶段动态博弈分析机组检修计划制定问题。
第一阶段,所有发电公司分别给出各自所有机组的检修计划。第二阶段,所有发电公司给出其拥有各机组的竞价策略并计算期望收益。第一阶段的检修计划为第二阶段制定竞价策略提供边界条件,同时第二阶段通过期望收益影响第一阶段的决策。
对动态博弈问题,要求均衡在整个博弈历史过程中都是最优的[16]。对应本文研究问题,机组竞价问题为该两阶段动态博弈问题的子博弈问题,因而机组检修计划取得均衡时,必然要求机组竞价策略取得均衡。这是以静态博弈模型分别讨论竞价均衡和检修均衡、而非直接求解动态博弈模型的依据,尽管分开讨论,但不改变动态博弈问题各阶段之间相互耦合的基本性质,与首先给定检修计划、再分析竞价策略有本质区别。
综上,该动态博弈问题可以转化为机组竞价均衡约束下的机组检修计划均衡求解问题,将动态博弈问题分解为两个静态博弈问题。由于竞价信息为私有信息,机组竞价策略均衡求解问题为不完全信息静态博弈问题;在竞价均衡基础上,各发电公司的期望收益可视为公共知识,所以检修计划安排为完全信息的静态博弈问题。图1给出了该问题的整体分析框架。
竞价均衡的存在性和唯一性决定了检修均衡求解的可行性。检修均衡的存在性影响机组检修行为的可预知性。检修均衡的结果直接关系到检修行为是否会对系统运行产生不利影响。竞价均衡分析和以竞价策略均衡为约束的检修均衡分析是探讨检修行为对系统影响的前提。
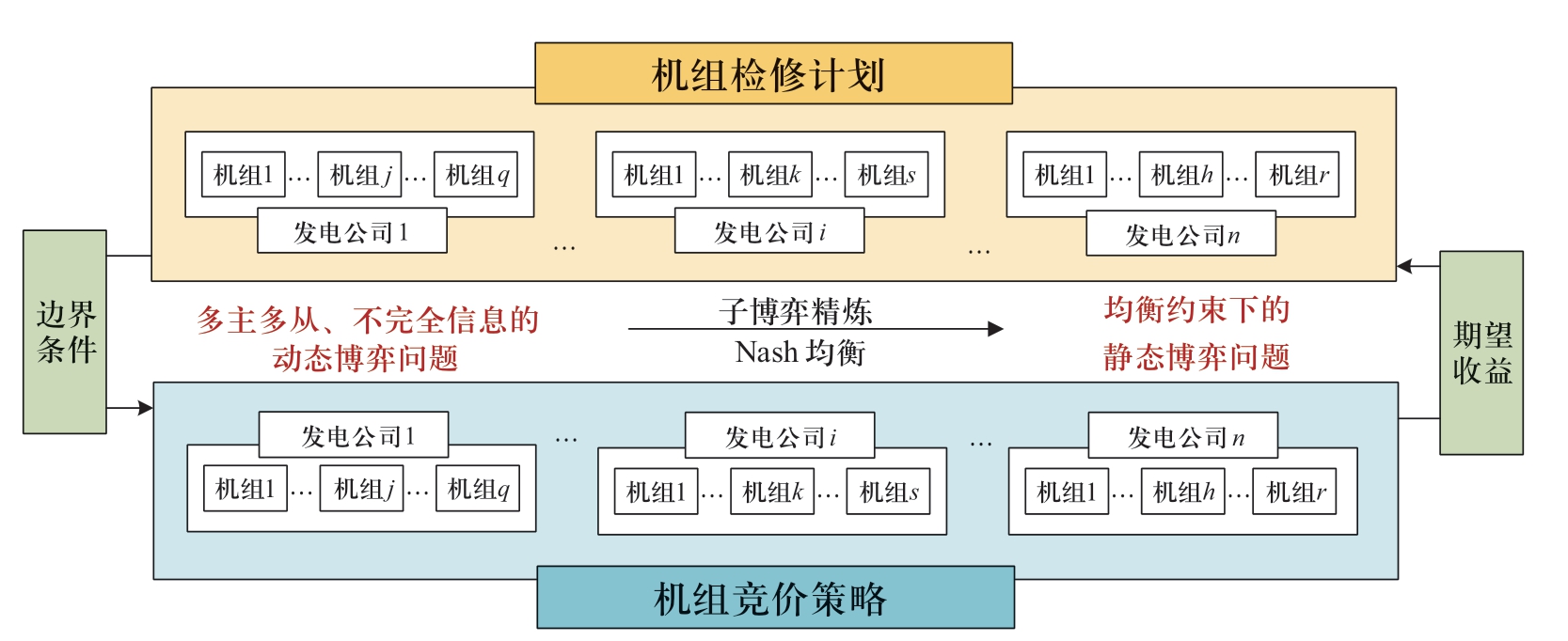
图1 基于博弈论的问题分析框架
Fig.1 Problem analysis framework based on game theory
3 竞价策略制定
3.1 模型假设
竞价策略均衡分析采取如下假设:
1)机组的竞价为发电公司的私有信息,而各机组的边际发电成本、发电能力、竞价上限和竞争电量为公共知识。考虑到发电公司基于实际投资经验估计其他发电公司成本以及发电量的可能性,该假设具有一定的合理性。
2)各机组竞价相互独立,服从均匀分布。
3)竞争电量不大于竞争机组的总发电量。
4)满足第1章所述的中长期合同竞价市场的基本规则。
3.2 数学模型
设有n个发电公司,第i个发电公司拥有mi台发电机组,每个发电公司需要为其拥有的每台机组确定竞价,制定竞价策略的目的是最大化其期望收益,期望收益取决于竞争得到的合同电量和对应的市场出清电价。对发电公司i,其竞价策略均衡为
式中:bi*=[b1*,b2*,…,b*mi]T为发电公司i的竞价,由其拥有的mi台机组的竞价组成;Fi为发电公司i的期望收益;Js为发电公司i拥有的第s台机组的期望收益。
机组s的期望收益为

式中:N为参与市场竞价机组数;Pr为所有机组竞价排序为第r种可能情况的概率,共有N!种排序组合;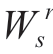 为第r种可能情况下机组s的合约电量;vr为第r种可能情况下市场出清电价;cs为机组s的发电成本。市场出清电价为满足式(3)条件时的机组s的竞价bs,即
为第r种可能情况下机组s的合约电量;vr为第r种可能情况下市场出清电价;cs为机组s的发电成本。市场出清电价为满足式(3)条件时的机组s的竞价bs,即![]()
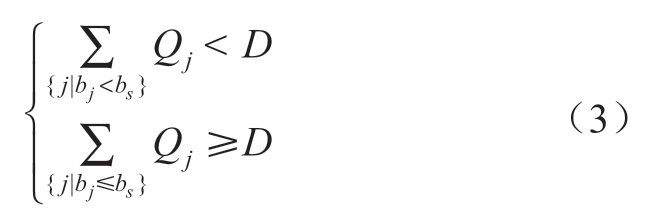
式中:Qj为机组j的预测发电量;D为竞争电量。
各机组的竞价从理论上可以在其发电成本和竞价上限之间的区间取得,但是低发电成本机组以高发电成本机组的发电成本作为竞价时的期望收益总是不劣于以更低的价格作为竞价时的期望收益,则可以认为所有机组的竞价区间为[cm,bm],其中,cm为所有机组中的最高发电成本,bm为竞价上限。
式中:ci为机组i的发电成本。
3.3 竞价策略均衡分析
3.3.1 两机系统的解析推导
两机系统的机组发电量Q1、Q2与竞争电量D关系的情况数较少,便于直接解析求解,能够直接说明竞争电量、竞价上限等要素对均衡的影响。
设机组1和机组2的发电成本满足c1≤c2。对两机系统,按机组发电量与竞争电量关系可划分为4种情形讨论:
1)若D≤Q1且D≤Q2,则两台机组均在竞价比对方低时才有期望获得合约电量。
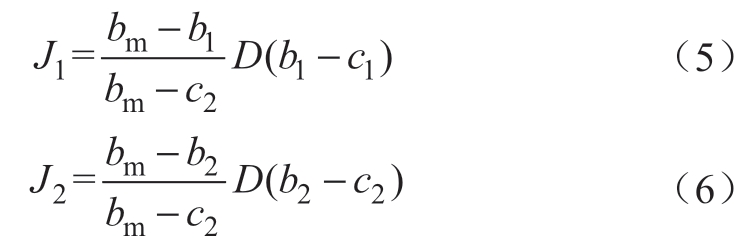
J1在b1∈R为凹函数(R为实数集),极值点为b1'=(c1+bm)/2;J2在b2∈R为凹函数,极值点为b2'=(c2+bm)/2。对机组2,b2'∈[c2,bm],机组2总是以(c2+bm)/2作为竞价;对机组1,若c2≤(c1+bm)/2,则机组1将以(c1+bm)/2为竞价,否则,将以c2作为竞价。
2)若D≤Q1且D>Q2,则机组1总可以得到合约电量,机组2只能在其竞价较机组1低时获得。
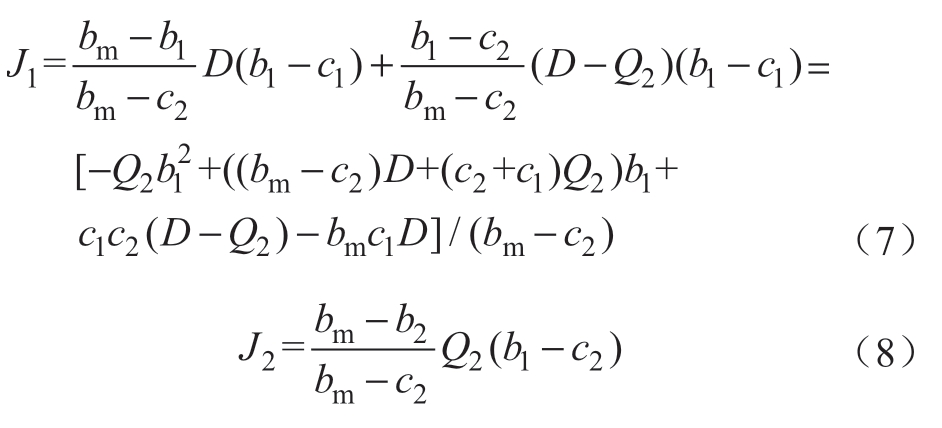
J1在b1∈R为凹函数,极值点为b1'=(c1+c2)/2+D(bmc2)/2Q2;J2在b2∈R为单调减函数。机组1的竞价取决于b1'与区间[c2,bm]的关系,而机组2总是以c2为竞价。
3)若D>Q1且D≤Q2,则机组2总可以得到合约电量,机组1只能在其竞价较机组2低时获得。此时结论与情形2)类似:机组1总是以c2为竞价,机组2竞价取决于极大值点b2'=c2+D(bm-c2)/2Q1与区间[c2,bm]的关系。
4)若D>Q1且D>Q2,则两台机组得到合约电量。

J1在b1∈R为凸函数,J2在b2∈R为凸函数,则J1与J2在[c2,bm]的极大值点总是在c2或bm处取得。具体在何处达到极大值,取决于期望收益在区间端点的函数值大小。容易验证,当有J(1c2|b2=bm)≥J(1bm|b2=bm)且J(2c2|b1=bm)≥J(2bm|b1=bm)时,存在多个均衡解。
需要说明的是,两台机组不可能都按边际发电成本进行竞价。若b1=c2
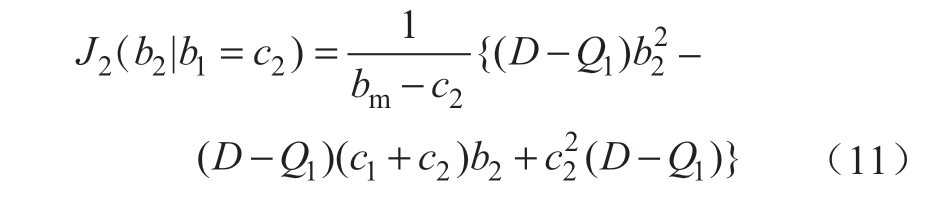
则有b2*=bm。对b2=c2的前提进行推导有同样结论。综上,两机系统竞价均衡必然存在,但可能不唯一。通过调整D和bm改变期望收益,可影响均衡解。
3.3.2 三机及以上系统的迭代求解
三机及以上系统的解析推导步骤与两机系统相同,但需要分析的情况数目明显增加。实际中常常采用循环迭代的方法求解。以3台机组(分属3个发电公司)需要检修为例,均衡求解流程见图2。
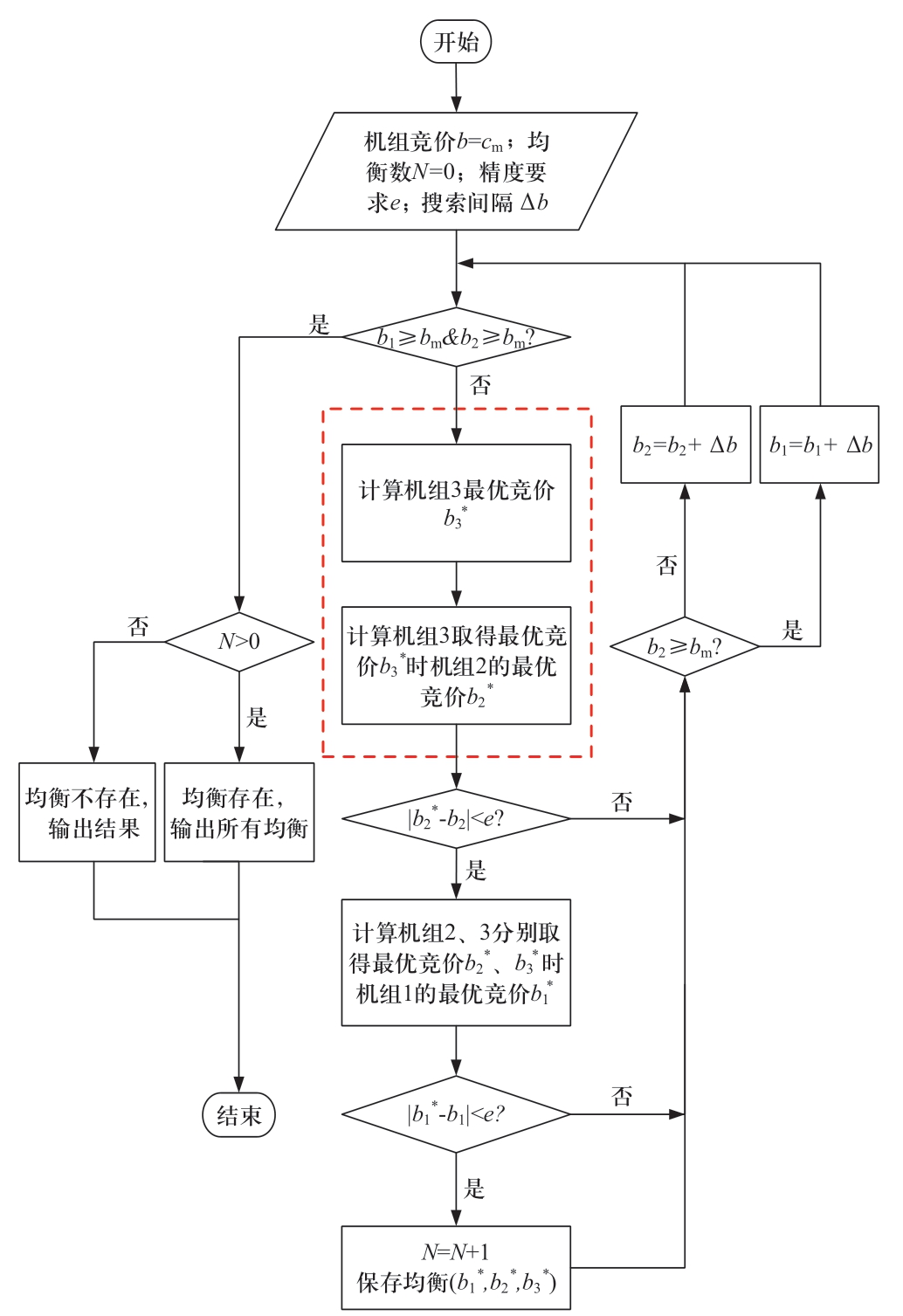
图2 三机检修均衡迭代求解流程图
Fig.2 Flow chart of equilibrium with three units based on iterative algorithm
求解式(1)需要分析N!种可能情形,使大规模系统的推导和求解变得困难,本文主要就两机和三机系统进行分析,三机系统的讨论主要用于反映两机系统无法体现的从属关系影响。文中的三机可以是等值后拥有不同参数的聚合机组。
对于三机分属两发电公司的情形,均衡求解流程类似图2,以发电机组2和发电机组3属于同一发电公司为例,只是b2*和b3*需要共同优化使得(J2+J3)取得最大值,如红色框线部分所示,且只需对b1进行循环。
若三机同属一家发电公司,则该发电公司垄断市场。为最大化其收益,其竞价策略将使市场总是以竞价上限作为出清电价,并且总是优先安排低成本机组。这种情况下,竞价策略不孤立,但此处主要关注期望收益,因为其同时可以反映电网购电成本,从而不再关心具体机组的竞价。
检修策略均衡的求解需在各时段竞价策略均衡存在且唯一的前提下才具备可行性。三机及以上系统的均衡可能不存在(除去同属一家发电公司的情形),即使存在也可能不唯一。均衡依赖于竞争电量和机组发电量的关系,并由受竞争电量和竞价上限影响的期望收益决定,通过调整市场要素,可改变均衡。
4 检修计划制定
4.1 模型假设
1)各机组的检修时长为确定的公共知识。
2)每台机组每年必须安排一次大修。
3)检修必须连续进行。
4)不考虑检修资源的限制。
5)各时段竞价策略均衡存在且唯一。
4.2 数学模型
各发电公司在制定检修计划时,考虑的是最大化总期望收益。由于各机组的检修时长设为公共知识,各发电公司只需确定各机组的检修起始时间。发电公司i的检修策略均衡为
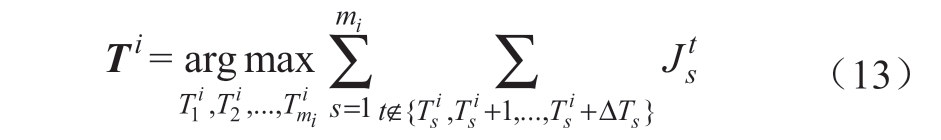
式中:![]() 为发电公司i的mi台机组的检修起始时间;ΔTs为第s台机组的检修时长;Jst为时段t机组s在竞价策略均衡下的期望收益。
为发电公司i的mi台机组的检修起始时间;ΔTs为第s台机组的检修时长;Jst为时段t机组s在竞价策略均衡下的期望收益。
4.3 检修策略均衡分析
基于收益矩阵的“划线法”[16]求解Nash均衡的思想,容易验证两机系统下检修策略Nash均衡必然存在。三机系统(除去同属一家发电公司的情形)检修计划的Nash均衡不一定存在,原因是引入了2台机组竞争和3台机组竞争时期望收益的比较。
如果纯策略Nash均衡不存在,意味着此时机组的检修行为在中长期合同竞价市场环境下不具有一致预测性,从数学上可认为各机组的检修计划完全随机,可能出现在负荷高峰等时段检修的不合理行为,给系统运行带来不可预测的风险。若考虑在一定概率下可能出现的最恶劣检修情形对系统运行的影响是可承受的,则认为尽管检修策略均衡不存在,也不会对系统运行带来致命影响。
检修策略均衡的唯一性未得到保证,即便存在多均衡,只要不对系统运行产生严重的不利影响,在工程上是可接受的结果。
5 机组检修行为对系统运行影响的评估
5.1 发电系统的可靠性
可靠性是检修计划制定的核心指标。由于中长期合同竞价市场以电能为基础,前述竞价策略和检修计划求解考虑的都是电量,本文对系统可靠性的衡量主要借助电量不足概率(loss of energy probability,LOEP)以及电能不足期望值(expected energy not supplied,EENS)指标。
5.2 系统供电的经济性
系统运行的经济性主要采用系统单位期望购电成本来反映,在数值上对应所有机组期望收入之和与竞争电量的比值:
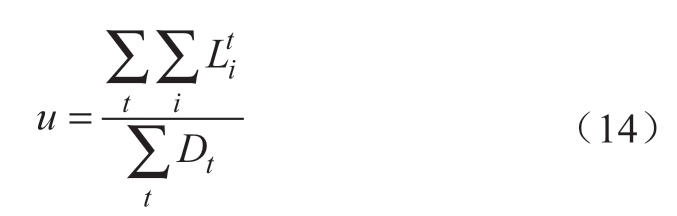
式中,Lit为机组i在时段t的期望收入。
5.3 基于两机三时间段的解析推导
假设(1,2)是一个纯策略Nash均衡,1表示机组A在时段1检修,2表示机组B在时段2检修,两机检修时段均为1。两机发电成本满足cA≤cB。
根据表1,则有

式中,下标表示机组,上标表示时段,括号中第1个和第2个数字分别表示机组A和机组B的检修时段。如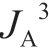 (1,2)表示机组A在机组A于时段1检修、机组B于时段2检修时在第3个时段的期望收益。
(1,2)表示机组A在机组A于时段1检修、机组B于时段2检修时在第3个时段的期望收益。
表1 两机三时间段的收益矩阵
Table1 Payoff matrix for two units and three time periods
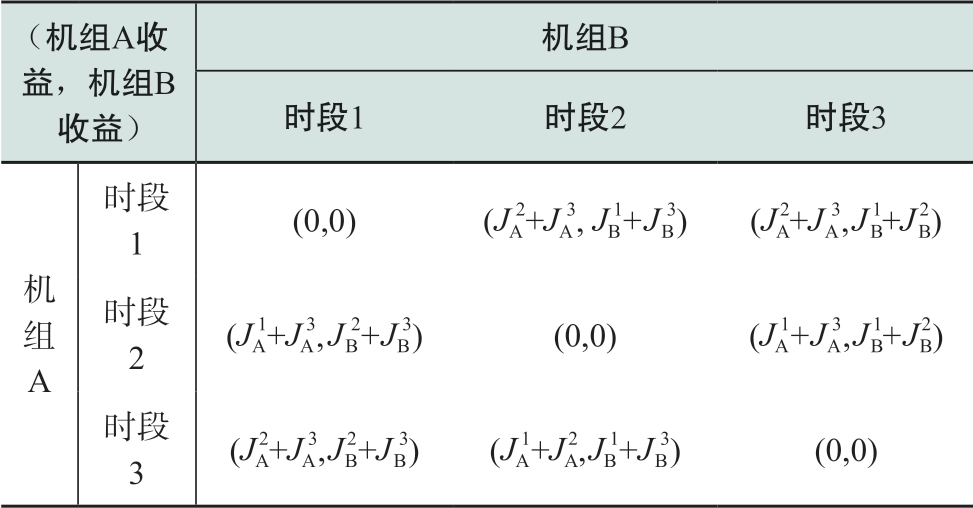
由Nash均衡的要求,代入两机参与市场竞争下的期望收益表达,则
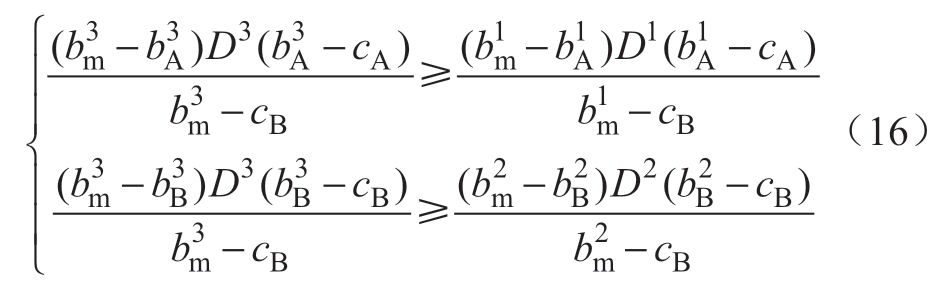
若考虑有cA+bmi>2cB,i∈{1,2,3},得:
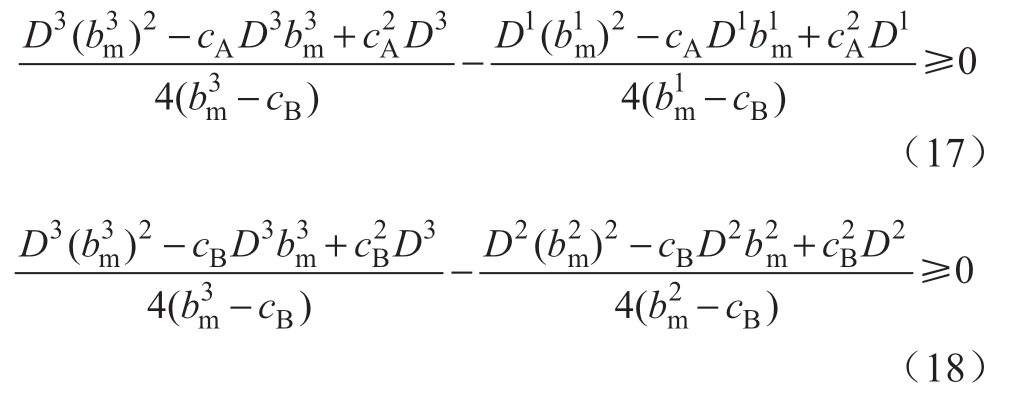
假设cA=cB,化简有
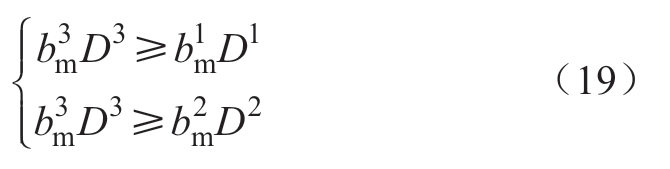
式(19)反映出:①上述讨论不涉及检修均衡(1,2)可能带来的风险,意味着可能出现时段1或时段2为备用较为紧缺的时段,如负荷高峰时段,此时机组安排检修将对供电可靠性产生不利影响。另外,如果该时段对应丰水期,还可能意味着排量的增加。②上述讨论不限定每个时段的竞价,意味着可能出现市场电价以竞价上限出清的时段,如3.3节推导所示,对系统运行的经济性造成不利影响。但实际是否会发生上述可能情形,依赖于中长期合同竞价市场中的参数取值和机组发电特性。
6 算例分析
6.1 算例系统
目前,火电机组和大型水电机组的检修计划需要提前报备系统调度机构,因而本文算例系统只包含火电机组和水电机组。
为了反映中长期合同竞价市场下机组检修行为与传统利用等备用方法(此处是等备用能量)制定检修计划之间的差别,本文基于某水电富集省份的实际运行数据,设计了包含两台水电机组和一台火电机组的算例系统,竞争电量曲线为负荷曲线的等比缩小结果,以半月为间隔,一个时间间隔内,火电1的发电能力为72 GWh,水电2的最大发电能力为52.2 GWh,火电3的发电能力为21.6 GWh,最大竞争电量为83.98 GWh。
取3台机组的发电成本分别为0.2元/kWh(水电1)、0.3元/kWh(水电2)、0.35元/kWh(火电3);竞价上限设为0.48元/kWh;检修时长分别为1月、2周、1月;强迫停运率分别为0.000 5、0.000 01、0.000 6。
6.2 不同从属结构下的检修计划及其对系统运行的影响
为了反映市场环境下检修计划安排的特点,求解4种情形下机组的检修起始时间:①三机分属三家发电公司;②水电机组1属于发电公司1,水电机组2和火电机组3属于发电公司2;③三台机组均属于同一发电公司;④依据等备用原则安排机组检修。对应4种情形下,发电可靠性指标处于最不利情形时的检修均衡及各指标如表2所示。
市场环境下的检修安排和电量供应从供电可靠性和经济性上都要劣于垂直管理模式下按等备用原则制定的检修计划和按经济性最优原则安排的电量计划。
表2 各从属情形下检修计划均衡及相应指标
Table2 Maintenance scheduling and corresponding indices under different belonging scenarios
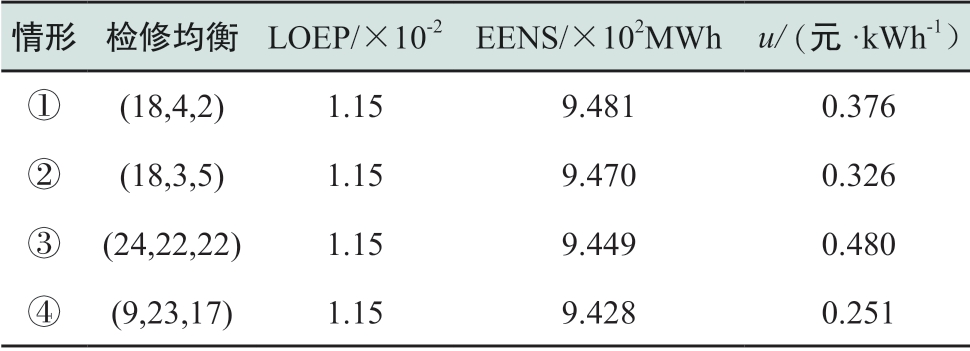
随着垄断程度的提高,电网购电成本将被抬升,极端情形对应情形③,按竞价上限作为最终市场边际价格。但供电可靠性不一定随垄断程度提高而降低,这与市场环境下的检修计划制定不面向可靠性有关。只有发电公司自主确定的检修时段恰与系统备用紧缺的时段发生重合,检修计划才会对系统供电可靠性造成较严重的不利影响。
6.3 检修时长对检修计划的影响
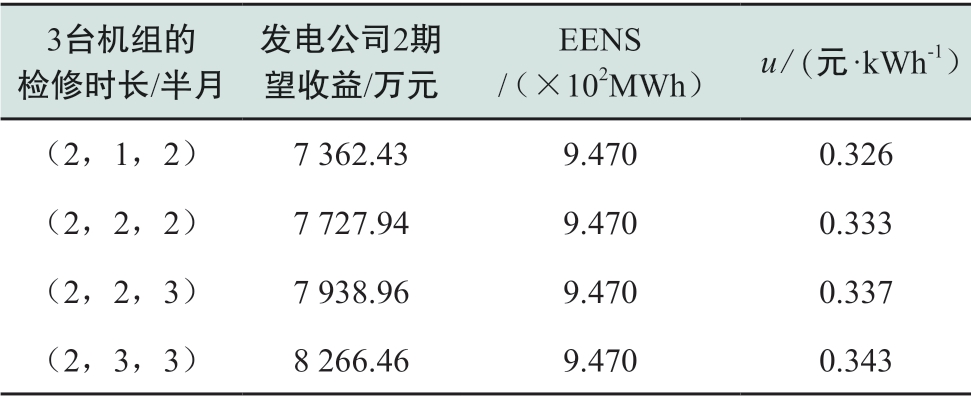
检修时长是机组检修计划的关键组成要素,对系统运行也会造成影响。如表3给出了调整发电公司2(拥有机组2和机组3)的机组检修时长后,其期望收益和系统运行情况。
发电公司2通过增加所拥有机组的检修时长,可望增加期望收益,与此同时,电网单位期望购电成本上升。在算例背景下,最恶劣情形下的供电可靠性几乎不受影响。
表3 发电公司2调整机组检修的结果
Table3 Results for maintenance adjustment of power generation company 2
6.4 检修机组发电能力对检修计划的影响
实际大型发电系统中,同一时段参与检修的机组占比往往较小,因而有必要探讨检修机组的发电能力对检修计划的影响,以及因此造成的系统运行影响差异。发电系统的可靠性在检修机组容量较小的情况下变化不大,本节着重关注系统运行的经济性。
假设某发电系统中的发电机组由两个发电公司A、B占有,两发电公司分别持有QA、QB发电能力的火电机组,负荷电量需求为D。同6.1节的参数,设A、B所属机组的发电成本分别为cA=0.2元/kWh,cB=0.35 元/kWh,竞价上限bm=0.48元/kWh。
假设某一时段内不考虑机组检修,有D≤QA且D≤QB,则根据3.3.1节,此时市场出清电价v=0.415元/kWh。如果此时发电公司A中部分机组在该时段检修,满足QA≤D≤2QA,则此时市场出清电价b=0.35+0.13D/2QA。说明在这种情形下,检修机组的发电能力越大,市场出清电价越高。
在此基础上,如若发电公司B也有少量机组进行检修,使得QB≤D,则此时市场出清电价将达到竞价上限,即v=0.48元/kWh。
以上对市场出清边际电价的讨论成立的前提是负荷电量与发电量不等式关系成立,而与检修机组发电能力的绝对值无关。换而言之,即使检修机组的发电能力占系统总发电能力的比例很小,仍有可能导致系统运行经济性的明显恶化,这其实是由于改变了市场的垄断程度。
对多机系统,随发电公司持有机组发电能力和负荷电量需求组合的多样性增加,结果更为复杂,但同样存在检修极小发电能力机组导致经济性下降的可能。例如,3个发电公司拥有的发电能力分别为 40 MWh、44 MWh、84 MWh,竞争电量为84 MWh,按6.1节的竞价上限和机组发电成本假设,此时市场出清电价为0.404 9元/kWh,但只要发电机组2通过检修略微减小发电能力,市场出清电价将抬高至0.48元/kWh,而发电公司2的期望收益将升高67%,发电公司2有理由在此时安排检修。
从另一方面也说明,竞价上限bm和竞争电量D的合理设置十分重要。例如在上例三机系统中,只要把竞争电量D调整为85 MWh,则市场出清电价将降至0.35元/kWh,调整竞价上限可减小检修带来的出清电价增幅。
7 结论
本文分析了中长期合同竞价市场下,以个体收益最大化为目标的机组检修行为,分析了市场环境下机组检修行为对系统运行可靠性和经济性的影响,并探讨了市场要素调整的影响。
研究表明:①市场环境下,完全由发电公司自主确定检修行为,从供电可靠性和经济性都可能劣于垂直管理模式,且性能表现与市场中检修机组对发电公司的从属结构有关;②发电公司存在故意延长检修时长以增加其发电收益的可能性;③即使检修机组的发电能力很小,在发电能力与竞争电量满足特定关系的情况下,可能导致经济性的明显恶化,反映出合理设置竞争电量与竞价上限的必要性。
参考文献
[1] SADEGHIAN O,OSHNOEI A,NIKKHAH S,et al.Multiobjective optimisation of generation maintenance scheduling in restructured power systems based on global criterion method[J].IET Smart Grid,2019,2(2): 203-213.
[2] PJM Energy Market.PJM Manual 10: Pre-Scheduling Operations[R/OL].Valley Forge: PJM,2019.https://www.pjm.com/-/media/documents/manuals/m10.ashx.
[3] CHATTOPADHYAY D.A game theoretic model for strategic maintenance and dispatch decisions[J].IEEE Transactions on Power Systems,2004,19(4): 2014-2021.
[4] CHATTOPADHYAY D,ALPCAN T,JEPPESEN M,et al.Electricity market implications of a least-cost carbon abatement plan: an Australian perspective[J].The Electricity Journal,2014,27(8): 105-115.
[5] TAYLOR J.,VanDoren P.Electricity Pricing in Transition[M].Boston: Springer,2002: 245-265.
[6] 国家能源局.国家发展改革委 国家能源局关于印发《电力中长期交易基本规则(暂行)》的通知[EB/OL].[2016-12-29].http://zfxxgk.nea.gov.cn/auto81/201908/t20190820_3692.htm.
[7] 陈晨.大用户电力中长期交易决策的理论与方法研究[D].北京:华北电力大学(北京),2019.
[8] BAHRAMI F,MOAZZAMI M,SHAHINZADEH H,et al.The maintenance scheduling in deregulated power systems with operational and practical constraints[C]//2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation(KBEI),December 22,2017.Tehran.IEEE,2017.
[9] FENG C Y,WANG X F.A competitive mechanism of unit maintenance scheduling in a deregulated environment[J].IEEE Transactions on Power Systems,2010,25(1): 351-359.
[10] MANBACHI Moein,MAHDLOO Faezeh,HAGHIFAM Mahmood-Reza.A new solution for maintenance scheduling in deregulated environment based on lost opportunity cost of market participation and reliability[C]//2010 International Symposium on Modern Electric Power Systems,Wroclaw,2010.
[11] 贾德香,程浩忠,严健勇,等.基于博弈论的发电公司检修决策[J].电力系统自动化,2007,31(1):27-32.
JIA Dexiang,CHENG Haozhong,YAN Jianyong,et al.Maintenance strategies for generation companies based on game theory[J].Automation of Electric Power Systems,2007,31(1): 27-32(in Chinese).
[12] FOTOUHI M A,MOGHADDAS TAFRESHI S M.Strategic maintenance scheduling of distributed generations in oligopolistic electricity markets[C]//2009 IEEE Electrical Power & Energy Conference(EPEC),October 22-23,2009.Montreal,QC,Canada.IEEE,2009.
[13] KIM J H,PARK J B,PARK J K,et al.A new game-theoretic framework for maintenance strategy analysis[J].IEEE Transactions on Power Systems,2003,18(2): 698-706.
[14] PANDZIC H,CONEJO A J,KUZLE I.An EPEC approach to the yearly maintenance scheduling of generating units[J].IEEE Transactions on Power Systems,2013,28(2): 922-930.
[15] 王盛煜.发电企业电力产品中长期交易决策理论与方法研究[D].北京:华北电力大学(北京),2019.
[16] 梅生伟,刘锋,魏韡.工程博弈论基础及电力系统应用[M].北京:科学出版社,2016: 94-126.
Self-determined Unit Maintenance Scheduling and Its Influence on System Operation in Medium- to Long-term Contract Bidding Market
LIN Yisha1,LU Zongxiang1*,QIAO Ying1,MA Ming2
(1.State Key Lab of Control and Simulation of Power Systems and Generation Equipment,Department of Electrical Engineering,Tsinghua University,Haidian District,Beijing 100084,China; 2.State Grid Gansu Electric Power Company,Lanzhou 730070,Gansu Province,China)
Abstract: The question of whether power generation companies should determine unit maintenance scheduling(UMS)remains controversial.Compared with the method under planned economy,in which system reliability alone is optimized,the maintenance plan declared by power companies may introduce risks to system operation since it guarantees only feasibility but not optimality.This paper focuses on the impact of selfdetermined UMS on system operation in the medium- to longterm contract bidding market.A method based on the game theory of unit bidding and maintenance strategy is proposed to simulate the maintenance behavior of units.Based on the results,the reliability and economic performance of the method are evaluated.The performance is better than that under vertical management mode.In addition,the method addresses the problem of power companies deliberately extending maintenance time in an attempt to raise the electricity price.We also found that a surge in electricity price occurs when only a small proportion of units are maintained,which is related to the unreasonable setting of competitive energy and auction cap.
Keywords: medium- to long-term contract bidding market; unit maintenance scheduling; game theory; system operation
作者简介:

林弋莎
林弋莎(1996),女,博士研究生,主要研究方向为新能源、多能互补,E-mail:lys_ncepu@126.com。
鲁宗相(1974),男,博士,副教授,主要研究方向为电力系统可靠性、风电/太阳能发电并网分析与控制、分布式电源及微电网、能源与电力宏观规划。通信作者,E-mail:luzongxiang98@tsinghua.edu.cn。
乔颖(1981),女,博士,副教授,主要研究方向为新能源、分布式发电、电力系统安全与控制,E-mail:qiaoying@tsinghua.edu.cn。
马明(1983),男,工程师,主要研究方向为电力系统运行及新能源发电,E-mail:mingwq@qq.com。
(责任编辑 张宇)
