0 引言
随着传统化石燃料面临资源紧张、污染严重等问题,风电、光伏等分布式电源(distributed generation,DG)快速发展[1],越来越多的DG接入电网,形成多DG相互协调的分布式可再生能源系统,使得电力系统的运行和控制愈加复杂[2]。高渗透率DG将带来配电网功率双向流动,DG出力的不确定性和间歇性也会影响电力系统的运行,从而影响电力系统安全。因此,需要对DG的运行特性进行分析以增强对配电网状态的感知。然而,由于成本限制等现实原因,调度中心无法在配电网中所有节点和线路均配置量测装置来获取系统状态,在实际中仅利用少量且有限类型的量测装置进行状态估计。因此,为了实时监测系统状态并辅助配电网分析和运行,如何实现考虑DG特性伪量测的状态估计是一个亟需解决的关键技术问题。
除了缺乏足够的实时量测数据影响状态估计数据冗余度之外,受风速和光强度等自然因素的影响,DG出力通常具有不确定性,也会在状态估计中造成不可忽略的误差。同时由于地理相邻的风电和光伏出力有较强的相关性,而随着接入配电网的风电和光伏越来越多,其出力相关性也越来越复杂[3],这也将影响电力系统的运行状态[4]。总之,随着接入配电网的DG类型和数量的增加,这个问题将进一步复杂化。因此,除了不确定性之外,DG的伪量测建模亦需合理考虑其相关性产生的影响。
近年来,研究人员对DG的伪量测建模进行了大量研究。文献[5-7]根据权重较低的历史数据对DG进行伪量测建模,未考虑DG出力的不确定性和相关性。文献[8]提出了一种基于人工神经网络的伪量测建模方法。文献[9]使用区间数来分析和量化电力系统量测的不确定性,但是这种方法不能方便地应用于现在广泛使用的基于加权最小二乘法(weighted least square method,WLS)的状态估计。文献[10]建立了一种通过大量历史数据统计得到DG的概率密度函数(probability density function,PDF)描述伪量测不确定性的方法,这为DG不确定性建模提供了一种思路。文献[11-13]则在文献[10]的基础上,使用高斯混合模型(Gaussian mixture model,GMM)来描述DG出力和负荷功率的不确定性。但是,上述方法都没有考虑DG之间的相关性。因此,为了提高伪量测数据的准确性,考虑DG相关性的配电网状态估计值得进一步研究。
本文提出了一种考虑DG出力不确定性与相关性的伪量测建模方法,并将其应用于配电网状态估计中。首先,应用Pair-Copula模型,获得考虑相关性的DG出力概率密度曲线。然后,使用GMM模型从出力概率密度曲线中提取出相应的可用于状态估计的伪量测数据,以确保数据冗余。最后,通过对经修改的IEEE-14节点算例系统进行计算分析,验证了方法的有效性。
1 DG的伪量测建模
目前状态估计通常采用WLS方法,该方法假设量测误差服从高斯分布。事实上,由于DG出力的波动性和不确定性,其概率密度函数无法用任何特定的分布表示。DG出力之间的相关性也会影响DG出力预测的值,从而影响伪量测数据的取值。因此,为了获得更好的估计结果,应将其不确定性和相关性考虑进DG的伪量测建模之中。本文以风电为例,提出如图1所示的两种DG伪量测建模方法。
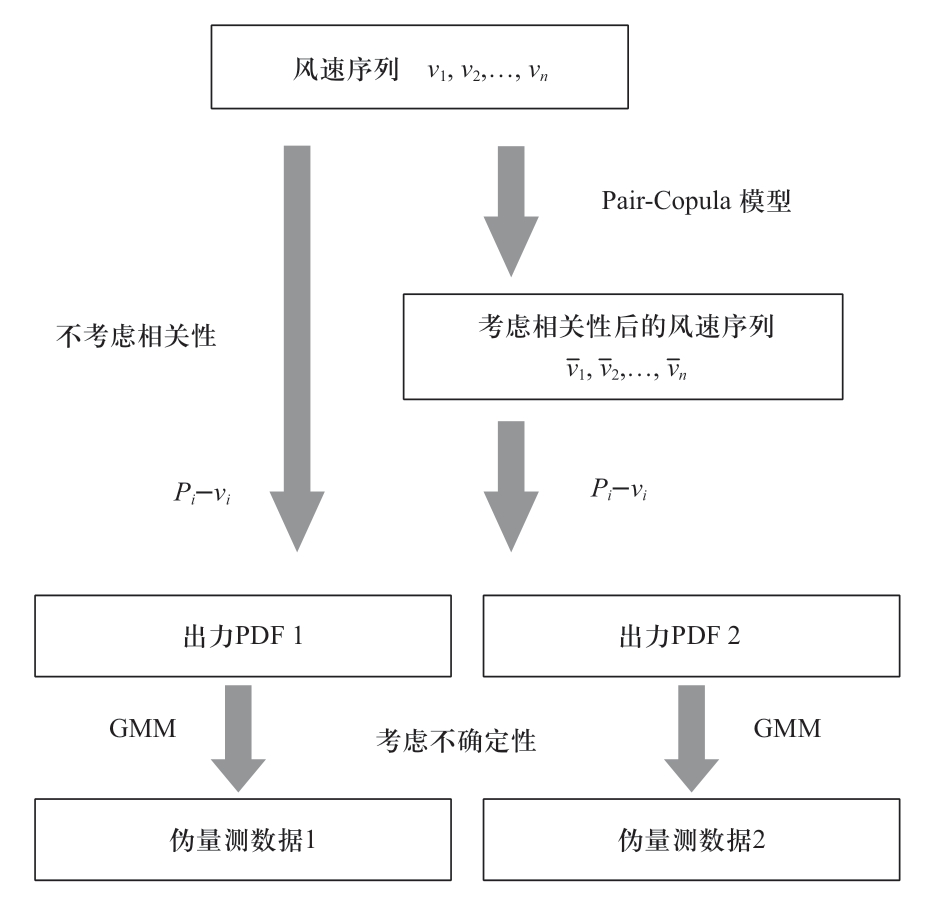
图1 DG伪量测建模过程
Fig.1 Process of Pseudo-measurements of DGs
下文将讨论这两种伪量测数据的建模对状态估计的影响,以分析考虑DG之间相关性和不确定性的重要性。
1.1 Pair-Copula模型
1.1.1 Pair-Copula结构
Copula是一类将随机变量的边缘分布函数连接起来,从而形成多元变量的联合概率分布函数[14]:
式中:Fi(xi)是随机变量xi的边缘分布函数;F(x1,x2,…,xn)是联合概率分布函数;C则是Copula 函数,是一个概率分布函数。
Copula的概率密度函数c的定义如下:
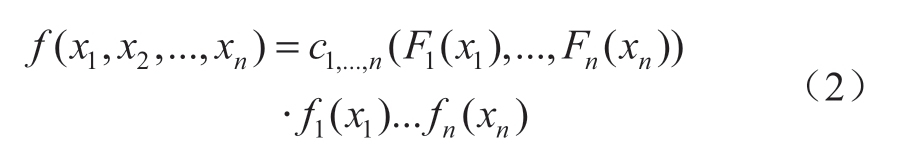
Copula函数通常包括Gumbel-Copula、Clayton-Copula、Frank-Copula、Normal-Copula和t-Copula等。Pair-Copula是一种结合多个Copula函数的构造方法[15],n维Pair-Copula函数具有n-1层,记为Li(i=1,2,…,n-1),每个节点都是Copula函数。令ui=Fi(xi),n维Pair-Copula结构如图2所示[15]。
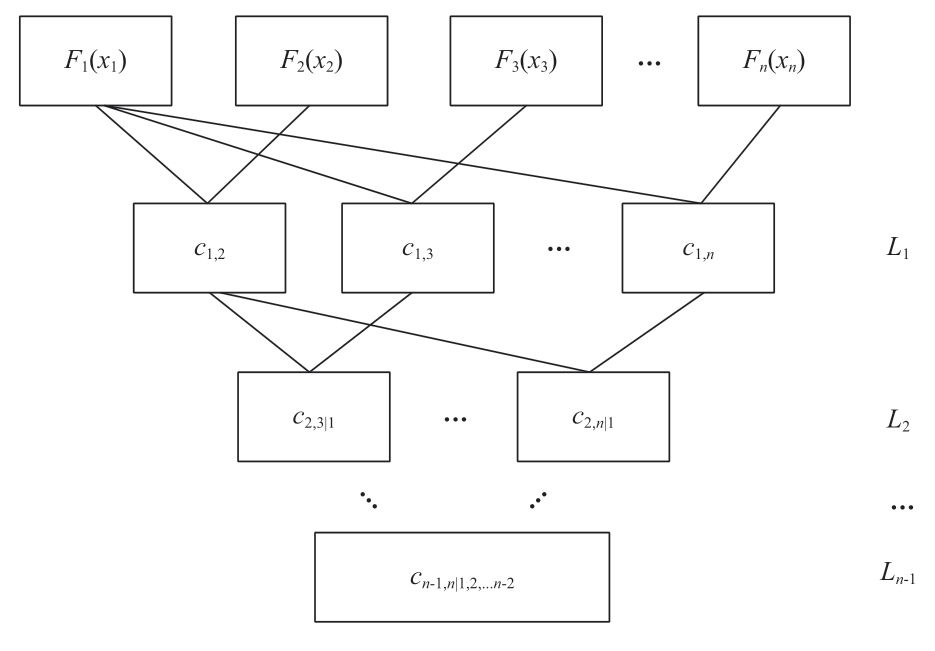
图2 n维Pair-Copula结构
Fig.2 Then-dimensional Pair-Copula structure
图2中,L1层c1,1+i为![]() 的缩写,其余层Li中,
的缩写,其余层Li中,![]()
![]()
![]() 的缩写。
的缩写。
根据Pair-Copula理论:
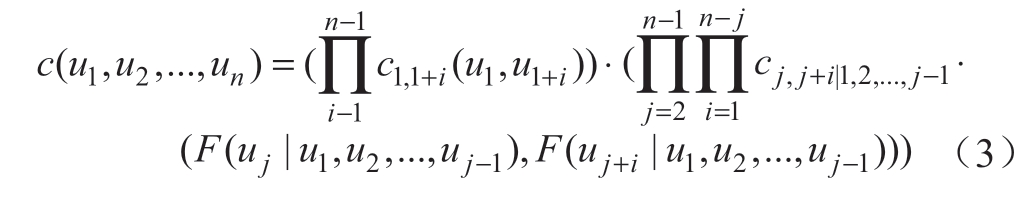
式(3)的条件分布性质可参见文献[15]。由此可见,Pair-Copula结构将随机变量两两合并,可引入多种Copula函数,从而提高风电相关性建模的拟合精度。
1.1.2 风电相关性建模过程
风电相关性可按如下过程进行建模。
1)获得风电单元w1,w2,…,wn中风速序列v1,v2,…,vn的边缘累积分布函数。
2)由Pair-Copula结构,建立风速联合分布模型。
3)对风速联合分布进行采样,以获得相关的风速采样序列![]()
4)建立风电单元wi的平均出力曲线Pi-vi,以获得考虑n个风电单元之间相关性的估计出力序列P1,P2,…,Pn。根据估计出力序列可以统计得到DG出力的PDF。
1.2 高斯混合模型(GMM)
非高斯分布DG的出力PDF难以直接应用在传统的WLS方法中。GMM可将不规则出力PDF逼近等效不同高斯分布函数的叠加,用等效后的出力PDF的均值和方差来描述出力的不确定性[11-13]。GMM原理如图3所示。在GMM中,服从任意分布的DG的PDF可以由不同的正态分布高斯子函数叠加进行等效:
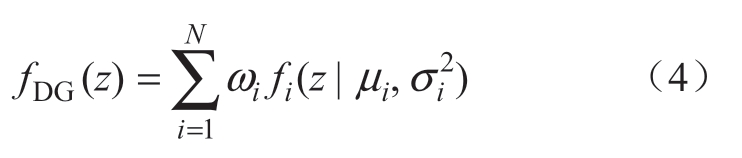
式中:N为高斯子函数的个数,ωi,μi,σi2表示每个子函数的权重、均值和方差。
同时这些子函数符合以下要求:
DG出力等效PDF的均值和方差求解如下:
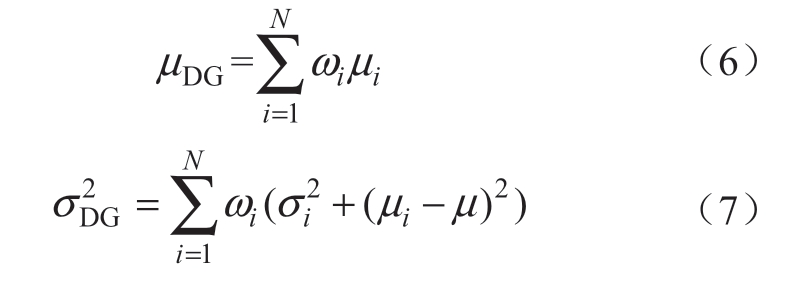
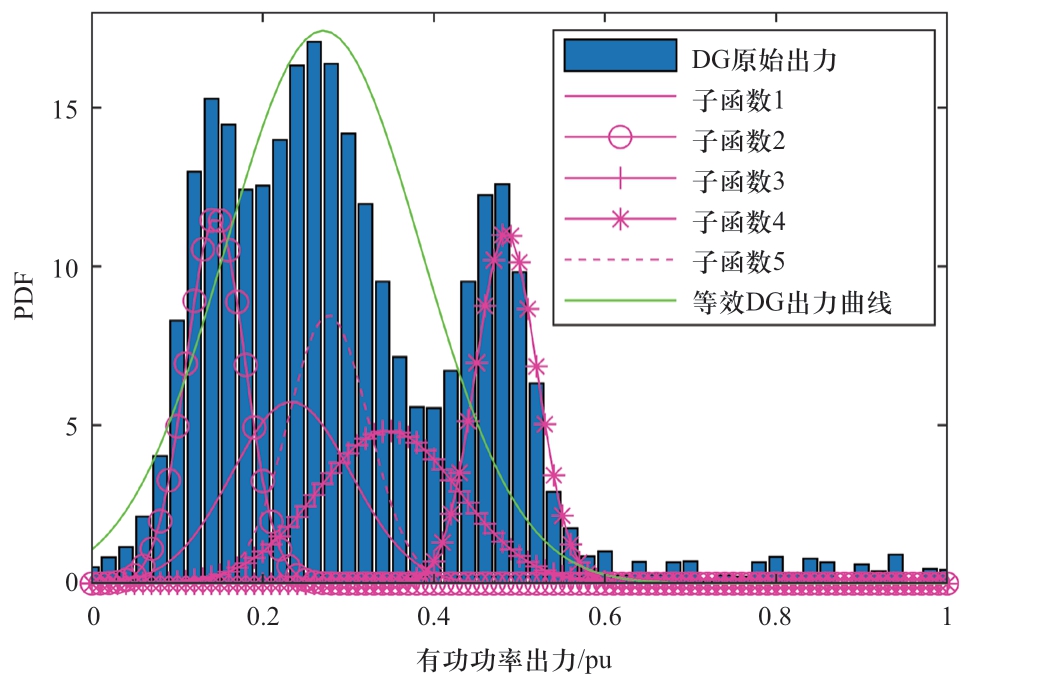
图3 GMM原理示意
Fig.3 Description of GMM theory
以此可以获得具有高斯分布的等效DG出力特性PDF,其均值和方差可用作伪量测数据,如式(8)所示。
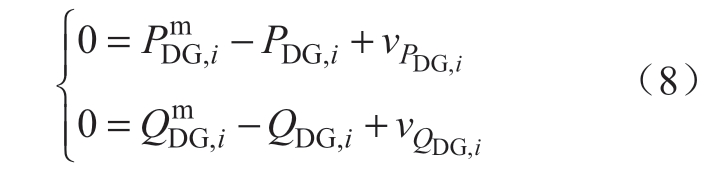
式中:vPDG,i、vQDG,i分别代表DG有功和无功功率PDG,i、QDG,i的量测误差。
因此,用GMM来描述DG不确定性的基本原理是用DG出力PDF的均值作为伪量测数据,替换具体时刻的实际出力PDG,i、QDG,i;用σD2 G替换协方差矩阵中的量测方差σ2(将在第2章讨论)进行状态估计。
2 状态估计算法
本文采用得到广泛应用的WLS进行配电网状态估计[16]。在配电网中,状态变量x通常选择为:
式中:θ为电压相角;v为电压幅值。
对于一般情况,状态估计的量测方程为:
式中:z为量测向量;e为量测误差向量,通常假设为独立不相关且满足均值为零的高斯分布;h(x)为状态变量和量测之间的函数。
在量测向量上,本文选择支路有功功率、支路无功功率、节点注入有功功率、节点注入无功功率和电压幅值作为量测数据进行状态估计,配电网中的量测方程具体表达式可参见文献[16]。
WLS通过求解以下最优化问题求取系统状态:
式中:R为协方差矩阵。该矩阵通常被假设为对角矩阵,每个对角元素Rii为第i个量测的方差σ2i。
使用高斯-牛顿迭代法得:
式中:k为迭代次数;x(k)为第k次迭代的状态向量;![]() 为雅可比阵;
为雅可比阵;![]() 为增益矩阵。
为增益矩阵。
将 Δx(k)= x(k+1) -x(k)代入式(12)得到:
3 算例分析
本文采用文献[17]的风电场数据对IEEE-14节点算例进行修改,采用陆上风电场A、B和海上风电场C分别取代节点2、3和6原有电源。风电场A和B的容量均为 48 MW,假设出力特性相同,基准值为50 MW;风电场C的容量为100 MW,基准值为100 MW。采用10天内各风电场的风速数据和出力数据,并转换成标幺值形式进行计算。系统基准值为100 MVA。本文电网结构如图4所示,讨论两种量测配置:量测配置1(图4中红色区域量测)和量测配置2(图4中红色区域和蓝色区域量测)。
3.1 Pair-Copula建模
使用Pair-Copula模型来考虑风电场A、B和C之间相关性的影响,通过三维Pair-Copula结构获得风电场之间风速的联合概率分布函数,根据Pi-vi曲线,从风速的联合概率分布函数获得风速采样序列。以风电场A为例,每隔1 min,随机采样50次,与实际出力数据进行比较,以验证Pair-Copula模型。结果如图5所示。
从图5可以看出,采用Pair-Copula模型后对风电场A的估计功率与实际出力更相近,而未采用Pair-Copula模型的估计功率曲线在转折处均与实际功率有较大偏差,不能很好地估计受其他风电场相关性影响的风电场出力。由此可见,本文采用的Pair-Copula方法可以有效预测风电场的出力趋势,有效追踪风电场之间的相关性。
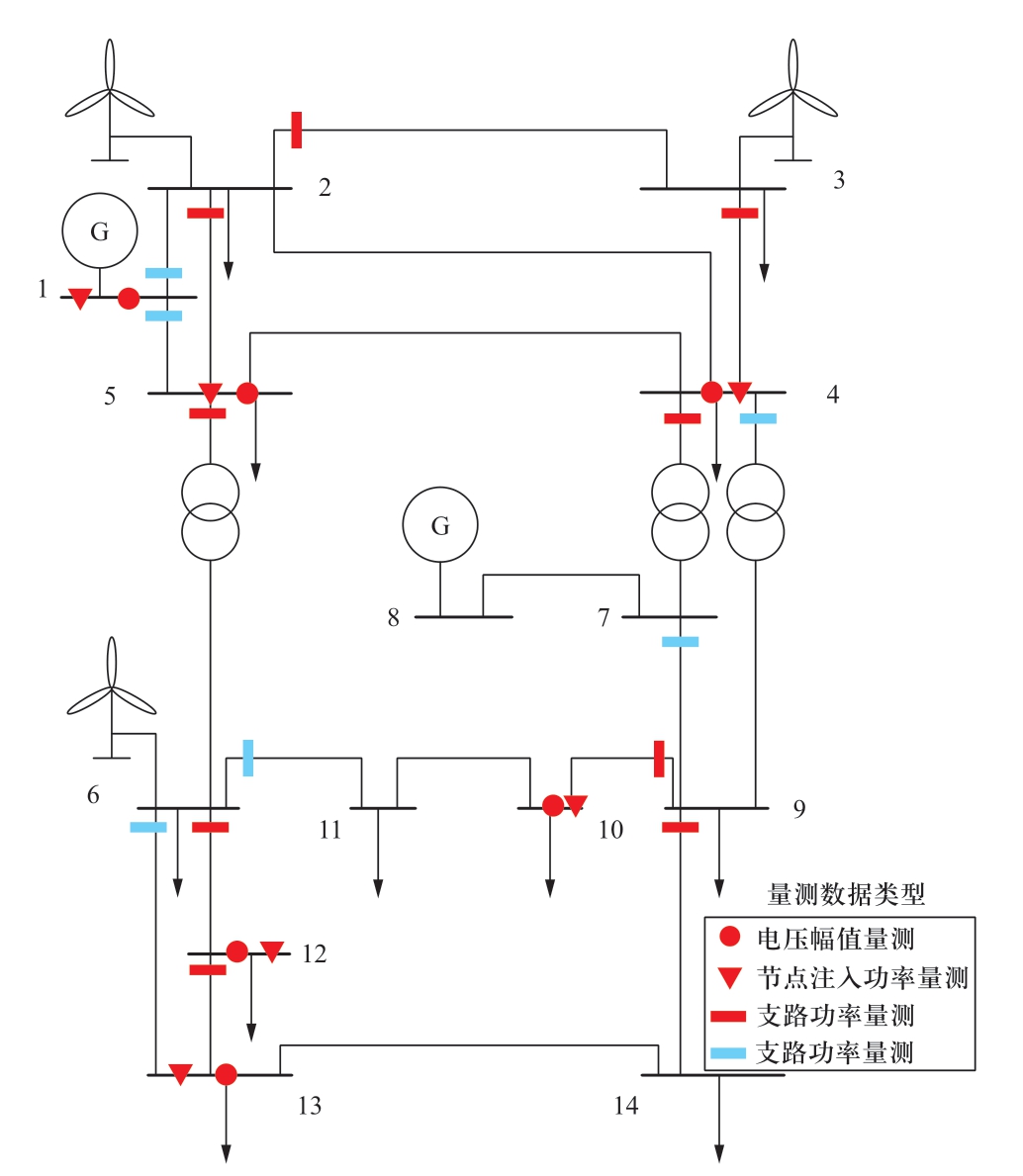
图4 电网结构图
Fig.4 Power grid structure

图5 风电场A的估计功率和实际功率
Fig.5 Estimated and actual power of wind farm A
3.2 GMM建模
使用Pair-Copula建模方法,可以获得具有相关性的风电场出力估计数据。在此基础上,采用GMM描述风电场的不确定性。以风电场A为例,GMM建模结果如图6及表1、表2所示。由此可获取3个风电场的伪量测数据。
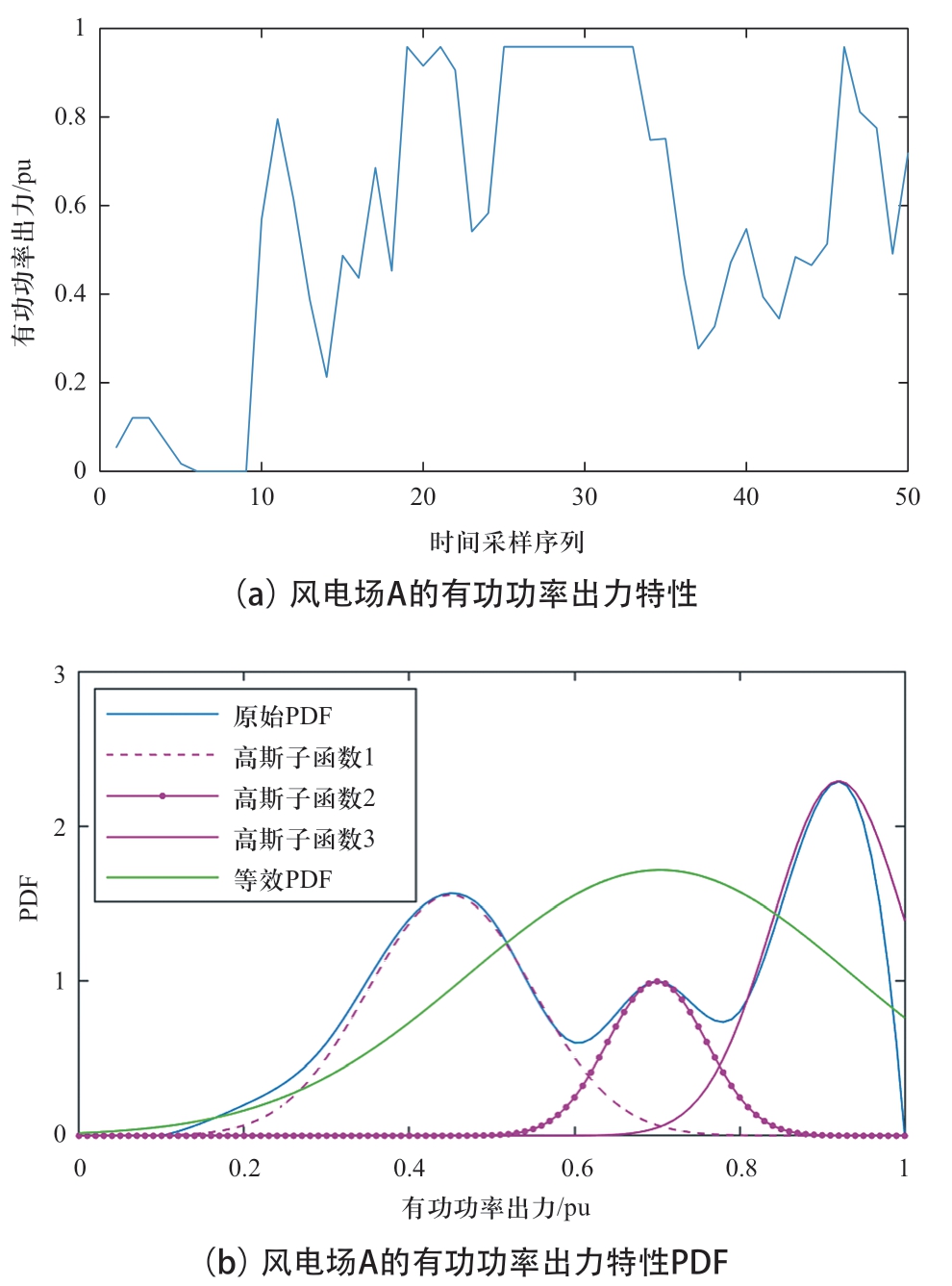
图6 风电场A的GMM建模
Fig.6 Gaussian mixture model of wind farm A
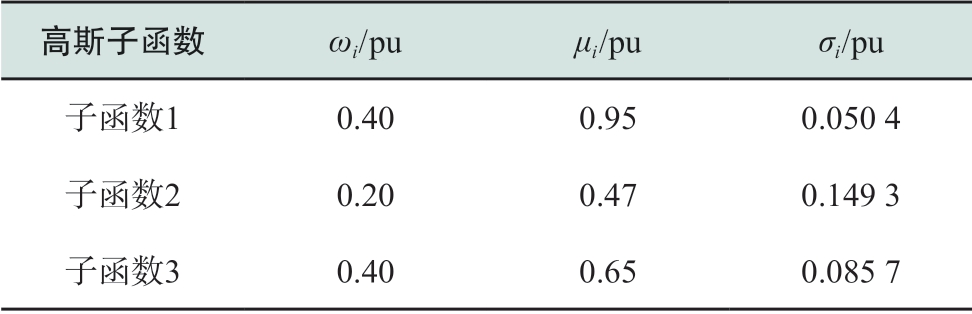
表1 风电场A、B的GMM建模参数
Table1 Parameters of the Gaussian mixture model of wind farm A and B

表2风电场C的GMM建模参数
Table2 Parameters of the Gaussian mixture model of wind farm C
3.3 配电网状态估计
先采取图4所示量测配置1来估计系统状态,相应的量测误差如表3所示。
表3 量测误差标准差
Table3 Standard deviation of measurement error

在本文中,绝对误差的平均值和最大值被用作状态估计的性能指标,性能指标的计算公式为[18]:

式中:N为系统中节点数量;xi,es、xi,actual分别为状态变量的估计值和实际值。
系统状态变量的真值由3.1节中50次随机取样风电场出力数据平均值而得。
为了验证Pair-Copula模型对DG出力之间相关性的描述,考虑以下3种方法。
方法1:未使用Pair-Copula模型及GMM进行状态估计(无伪量测)。
方法2:仅使用GMM进行状态估计(使用伪量测1)。
方法3:同时使用Pair-Copula模型和GMM进行状态估计(使用伪量测2)。
其中,方法2建模时认为各风电场之间无相关性,具有相同独立高斯分布,仅使用GMM对每个风电场的风速进行建模。3种方法仿真结果如表4和图7所示。
表4 量测配置1中3种方法状态变量的性能指标
Table4 Performance metrics of state variables of three methods in measurements arrangement 1

从表4可以看出,采用方法3的情况下,其电压幅值和电压相角的平均绝对误差和最大绝对误差要比方法1和方法2中对应的值要低。这是因为方法3通过Pair-Copula模型处理风速,有效地考虑到3个风电场之间的相关性。
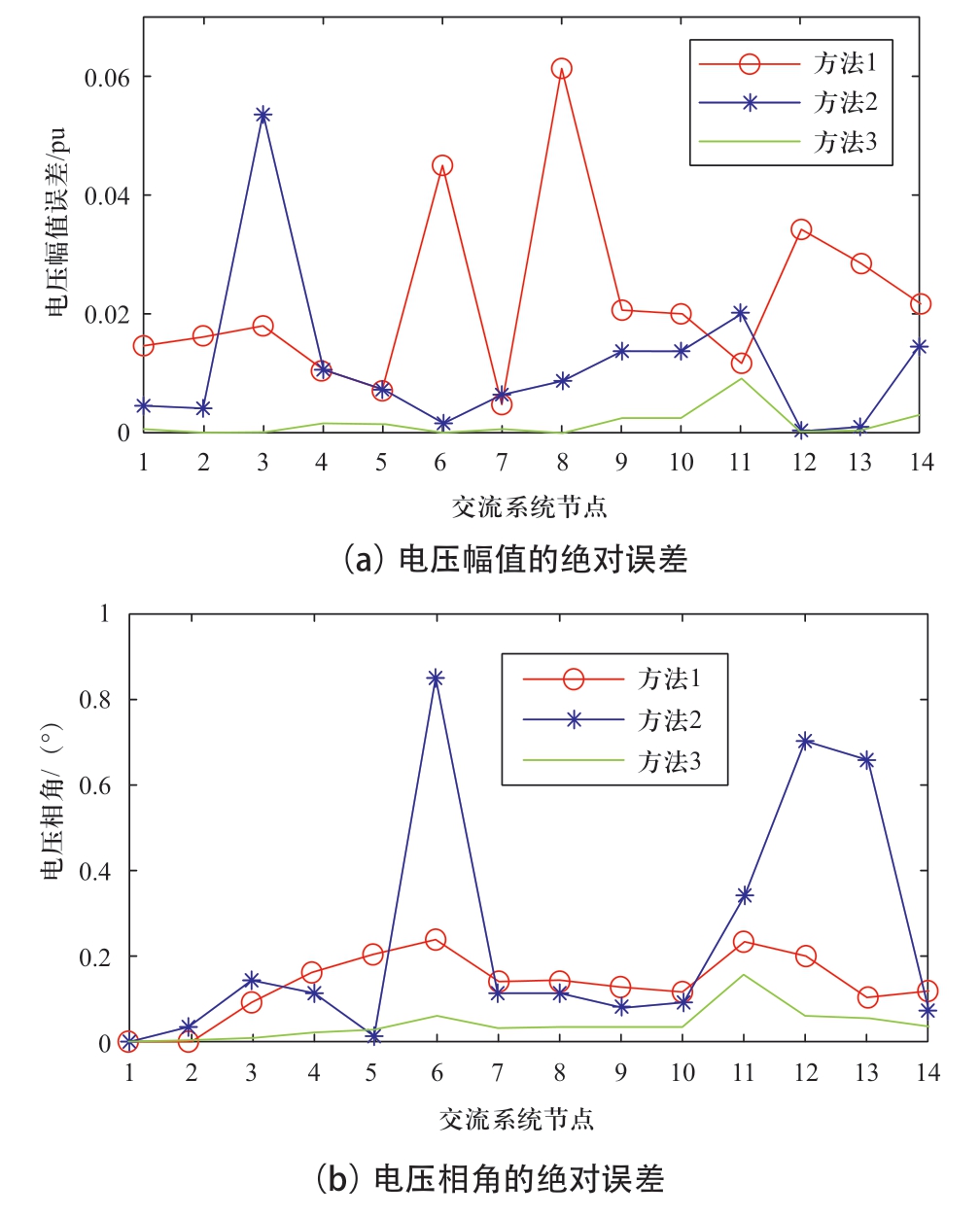
图7 量测配置1中3种方法的绝对误差
Fig.7 Absolute error of three methods in measurements arrangement 1
与方法1相比,方法2对电压幅值的估计精度更高,但其对电压相角的估计精度则要低于方法1,而估计结果精度由电压幅值和相角两方面构成,这表明方法2引入的不计相关性的伪量测数据并不能完全提高估计结果的精度。方法3可以使GMM更好地描述Pair-Copula模型过程中出力的不确定性。可以看出,考虑Pair-Copula可以使GMM对相关性增加的情况更敏感,且其强度更明显。换言之,Pair-Copula模型提高了GMM描述不确定性的能力。
考虑图4中的量测配置2,3种方法的仿真结果如表5和图8所示。
表5 量测配置2中3种方法的状态变量的性能指标
Table5 Performance metrics of state variables of three methods in measurements arrangement 2

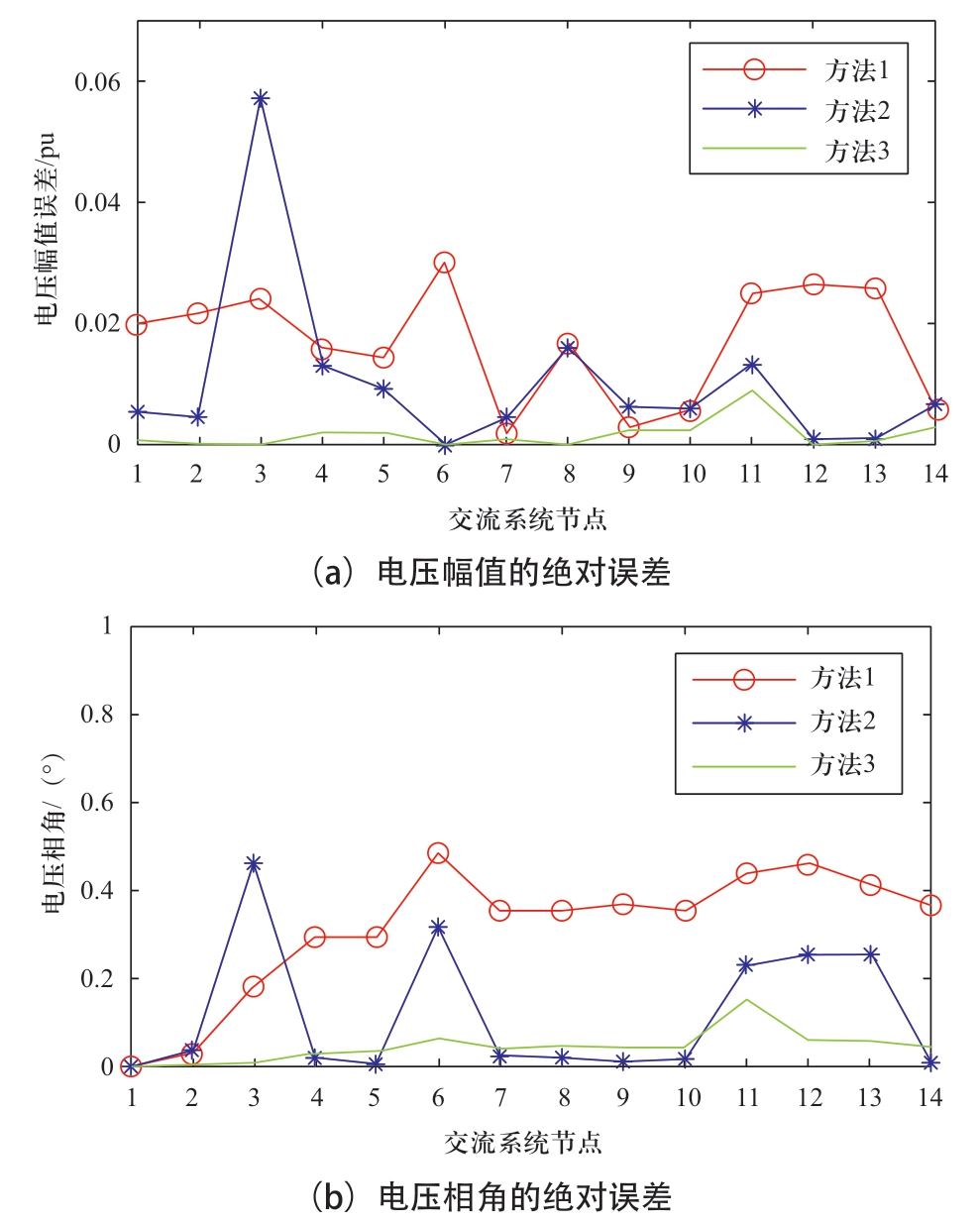
图8 量测配置2中3种方法的绝对误差
Fig.8 Absolute error of three methods in measurements arrangement 2
从表5和图8可以看出,随着量测的增加,方法3仍然是3种方法中电压幅值和电压相角的估计误差最小的方法。方法2的节点3和6处的节点电压幅值估计和电压相角估计效果不佳。这是因为认为每个风电场独立同分布后所得到的PDF计算出的伪量测数据与实际数据有出入,引入了不良数据,因此相应的节点误差较高。
比较图7和图8,可以发现方法1和方法2中的估计精度随量测配置的不同而变化,方法3则对量测配置具有一定鲁棒性,精度差异不大。这说明方法3考虑风电出力的相关性后,其伪量测数能更准确地反映电力系统运行的实际情况。因此,对DG进行有效的不确定性和相关性建模后得到的伪量测数据,可以弥补低数据冗余带来的不足从而获得良好的估计结果。
4 结论
随着DG的快速发展,接入电网中的DG由于存在量测装置不足、出力特性具有不确定性和相关性等特点,量测数据冗余度不足限制了状态估计精度的进一步提高。在系统中所有节点和线路配置量测装置不经济且不实际,因此本文提出了一种考虑DG出力不确定性和相关性伪量测建模的状态估计方法。该方法探究了DG出力的不确定性和相关性,基于Pair-Copula相关性模型和GMM不确定性模型进行伪量测建模,其得到的伪量测数据可显著提高状态估计结果的精度。该方法可应用于缺乏实时量测的情景,以及含多DG接入的配电网,并对量测配置具有一定鲁棒性。经修改的IEEE-14节点算例仿真计算结果验证了该方法的正确性和有效性。
参考文献
[1] 李隽,宋福龙,余潇潇.全球能源互联网骨干网架规划研究[J].全球能源互联网,2018,1(5):527-536.
LI Jun,SONG Fulong,YU Xiaoxiao.Research on global energy interconnection backbone grid planning[J].Journal of Global Energy Interconnection,2018,1(5): 527-536(in Chinese).
[2] 徐唐海,鲁宗相,乔颖,等.源荷储多类型灵活性资源协调的高比例可再生能源电源规划[J].全球能源互联网,2019,2(1):27-34.
XU Tanghai,LU Zongxiang,QIAO Ying,et al.High penetration of renewable energy power planning considering coordination of source-load-storage multi-type flexible resources[J].Journal of Global Energy Interconnection,2019,2(1): 27-34(in Chinese).
[3] WAN Y H,MILLIGAN M,PARSONS B.Output power correlation between adjacent wind power plants[J].Journal of Solar Energy Engineering,2003,125(4): 551-555.
[4] MORALES J M,BARINGO L,CONEJO A J,et al.Probabilistic power flow with correlated wind sources[J].IET Generation,Transmission & Distribution,2010,4(5): 641.
[5] SARIĆA T,RANKOVIĆA.Load reallocation based algorithm for state estimation in distribution networks with distributed generators[J].Electric Power Systems Research,2012,84(1): 72-82.
[6] RANKOVIC A,SARIC A T.Modeling of photovoltaic and wind turbine based distributed generation in state estimation[C]//15th International Power Electronics and Motion Control Conference(EPE/PEMC),Sep.4-6,2012.Novi Sad,Serbia.
[7] YANG X,LI Q,YUAN X D,et al.Active distribution system state estimation considering the characteristics of DGs[C]//5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies(DRPT),Nov.26-29,2015.Changsha,China.
[8] MANITSAS E,SINGH R,PAL B C,et al.Distribution system state estimation using an artificial neural network approach for pseudo measurement modeling[J].IEEE Transactions on Power Systems,2012,27(4): 1888-1896.
[9] 徐俊俊,吴在军,胡秦然,等.考虑多类型分布式电源和负荷不确定性的主动配电网区间状态估计[J].中国电机工程学报,2018,38(11):3255-3266.
XU Junjun,WU Zaijun,HU Qinran,et al.Interval state estimation for active distribution networks considering uncertainties of multiple types of DGs and loads[J].Proceedings of the CSEE,2018,38(11): 3255-3266(in Chinese).
[10] WOOLLEY N C,MILANOVIC J V.Statistical estimation of the source and level of voltage unbalance in distribution networks[J].IEEE Transactions on Power Delivery,2012,27(3): 1450-1460.
[11] VALVERDE G,SARIC A T,TERZIJA V.Stochastic monitoring of distribution networks including correlated input variables[J].IEEE Transactions on Power Systems,2013,28(1): 246-255.
[12] SINGH R,PAL B C,JABR R A.Statistical representation of distribution system loads using Gaussian mixture model[J].IEEE Transactions on Power Systems,2010,25(1): 29-37.
[13] LIU Q,DING L,WANG X H,et al.Distribution system state estimation considering the uncertainty of DG output[C]//2017 IEEE Conference on Energy Internet and Energy System Integration(EI2),Nov.26-28,2017.Beijing.
[14] LU Q Y,HU W,MIN Y,et al.Wind power uncertainty modeling considering spatial dependence based on Pair-copula theory[C]//2014 IEEE PES General Meeting | Conference & Exposition,July 27-31,2014.National Harbor,MD,USA.
[15] 吴巍,汪可友,李国杰,等.基于Pair Copula的多维风电功率相关性分析及建模[J].电力系统自动化,2015,39(16):37-42.
WU Wei,WANG Keyou,LI Guojie,et al.Correlation analysis and modeling of multiple wind power based on Pair Copula[J].Automation of Electric Power Systems,2015,39(16): 37-42(in Chinese).
[16] ABUR A,EXPOSITO A G,Power system state estimation: theory and implementation[M].Boca Raton,FL,USA: CRC Press,2004.
[17] 黄阮明,郭明星,郑秋宏,等.基于Copula相关性理论的集群风电并网建模方法[J].电气自动化,2019,41(1):23-27.
HUANG Ruanming,GUO Mingxing,ZHENG Qiuhong,et al.Modeling of cluster wind power integration based on Copula correlation theory[J].Electrical Automation,2019,41(1): 23-27(in Chinese).
[18] 王少芳,刘广一,黄仁乐,等.多采样周期混合量测环境下的主动配电网状态估计方法[J].电力系统自动化,2016,40(19):30-36.
WANG Shaofang,LIU Guangyi,HUANG Renle,et al.State estimation method for active distribution networks under environment of hybrid measurements with multiple sampling periods[J].Automation of Electric Power Systems,2016,40(19): 30-36(in Chinese).
State Estimation in Distribution Systems Considering Distributed Generation Uncertainties with Correlations
LI Jing1,LI Xingzhi2*,HAN bei2,LI Guojie2,WANG Zhilei1
(1.State Grid Shandong Jinan Electric Power Company,Jinan 250000,Shandong Province,China;2.Key Laboratory of Control of Power Transmission and Conversion,Ministry of Education,Shanghai Jiao Tong University,Minhang District,Shanghai 200240,China)
Abstract: The development of renewable energy resources(RESs)and distributed generation(DG)technology has brought more uncertainties to power systems and aggravated the problem of insufficient measurements in state estimation.In most studies,pseudo-measurement modeling is adopted to improve the measurement redundancy of the system.In view that the present pseudo-measurement modeling researches taking both uncertainty and correlation between DGs into consideration are relatively weak,this paper presents a DG pseudo-measurement model based on the Pair-Copula method to describe a wind power correlation,and a Gaussian mixture model(GMM)with an equivalent uncertainty to describe the uncertainty of the DGs.It was found that the developed method can improve the accuracy of pseudo measurements so as to improve the accuracy of state estimation for distribution networks.The results obtained based on a modified IEEE-14 bus network were analyzed and verified the correctness and validity of the proposed method,and showed that the proposed method can reasonably depict the uncertainty and correlation of DGs outputs in state estimation.
Keywords: state estimation; distribution system; Pair-Copula model; Gaussian mixture model; weighted least square method
作者简介:

李静
李静(1973),女,高级工程师,主要研究方向为电力系统规划与可靠性,E-mail:1930748682@qq.com。
李幸芝(1996),女,博士研究生,研究方向为电力系统状态估计。通信作者,E-mail:xz.li531@sjtu.edu.cn。
韩蓓(1984),女,博士,讲师,研究方向为含微网的配电网模型研究,E-mail:han_bei@sjtu.edu.cn。
李国杰(1965),男,教授,研究方向为新能源、电力系统、微电网、柔性直流输电的分析与控制,E-mail:liguojie@sjtu.edu.cn。
(责任编辑 李锡)
