0 引言
风电作为无污染可再生能源的代表,得到了广泛应用。然而,随着风电渗透率的不断增加,其随机性和不稳定性已经成为影响微网可靠运行及其电能质量的一个巨大挑战[1-3]。风电的峰谷特性及波动性亦给电力系统带来诸多负面影响[4-5]。
为了应对风电的随机性,文献[6]在研究电热负荷与风电出力分布特性的基础上,深入分析电热联合系统多源协调对风电消纳的影响,以风电消纳电量最大和系统运行成本最小为目标建立电热联合系统多源协调优化模型。文献[7]提出一种风电场与含储热的热电联产形成共同体联合运行的运行模式,并基于该运行模式提出了考虑风电出力不确定性的联合系统优化调度模型。文献[8]针对风电渗透率不断提高带来的风电消纳问题,提出了一种含抽水蓄能机组的鲁棒机组组合优化方法。文献[9]提出了一种通过需求侧管理激励负荷侧的高载能企业参与调峰,提高系统风电消纳能力的错峰峰谷分时电价机制。上述文献从不同角度提出了解决风电随机性问题的应对措施,在微网系统中,电储能由于能量密度高、易控制,是抑制风电随机性的常用方案。
储能系统的应用可以提高风电系统的可调度性,降低风电并入微网可能带来的运行风险[10-11]。文献[12]以提高风能资源利用率为主要目的,利用电池储能系统削峰填谷,改善系统负备用不足的现状以松弛电网调峰瓶颈,并分析了储能系统能够带来的电网多环节效益。文献[13]从发电侧和电网侧两方面入手,提出了一种储能参与的高比例风电互联电力系统分散式调度模型。文献[14]结合多场景随机规划和序贯蒙特卡洛模拟方法,提出了考虑储能寿命折损的风电场站内储能优化配置方法。上述文献采用储能有效提高了风电的消纳水平,但没有区分风电功率在长时间尺度上的峰谷特性及短时间尺度上的波动特性。
针对风电在长时间尺度上的峰谷特性及短时间尺度上的波动性,分别采用大功率大容量的储能单元以及小功率快速响应的储能单元。为充分利用储能的灵活可控能力抑制风电的随机性,文献[15]利用分频技术对风电场不平衡功率进行分解,根据系统所允许的最大频率波动确定系统高频功率波动分量,实现了能量型和功率型储能的功率分配和容量配置。文献[16]基于离散傅里叶变换对风电出力进行频谱分析,将风电出力分解成短时间尺度的高频分量和长时间尺度的低频分量,利用电池储能补偿风电高频波动部分,利用抽水蓄能参与系统调峰运行。文献[17]通过滑动平均滤波获得储能系统参考功率,将分解得到的高频信号和低频信号分配给超级电容器和锂电池。文献[18]针对不同风电出力场景下风电功率的波动特性,结合风电并网波动标准和混合储能系统性能特点,实现风电功率的自适应小波包分解和储能初级功率分配。然而,上述文献没有考虑风电功率预测误差随预测时间的延长而增大的特点,导致储能的优化控制策略与实际需求偏差较大。
模型预测控制(model predictive control,MPC)技术在处理风电预测误差随时间延长而增大的特性方面具有很大优势[19-22]。MPC又称为滚动时域优化控制,是一种基于模型的有限时域闭环最优控制算法[23]。其核心思想是:在每一个采样时刻,考虑系统未来有限时段的状态,使用当前时刻的测量值和预测模型,通过控制约束和目标函数,得到当前和未来有限时段的最优控制变量。在下一采样时刻,利用当前时刻控制后的测量数据重复这一优化过程[24]。文献[25]根据风功率预测结果制定风储集成发电系统期望输出,通过滚动优化计算得到下一调度周期内储能系统的控制指令。文献[26]建立了日前最优经济调度模型,同时为了校正可再生能源和负荷的预测偏差,基于MPC方法建立了以联络线功率偏差和储能荷电状态偏差最小为目标的日内滚动优化调度模型。文献[27]应用MPC算法平抑风电波动以达到并网要求,针对单组储能功率频繁充放电的情况,应用2组不同充放电状态的储能单元平抑风电波动。上述文献虽然运用储能及MPC技术处理风电功率的随机性,但是未考虑MPC技术的滚动时域及步长可以随不同风电功率的峰谷特性及波动特性进行调整,能达到更优的调节效果。
本文提出的基于MPC的储能系统多时间尺度动态响应优化技术,利用不同储能系统的容量与响应速度特性,滚动优化风电系统的输出功率。上层储能系统侧重调整风电功率在长时间尺度上的峰谷特性,其控制结果作为下层状态变量,下层储能系统侧重调整风电功率在短时间尺度上的波动特性。此外,在上下2层滚动优化过程中选取不同的滚动时域及预测步长,结合离散傅里叶变换所得的幅频特性曲线,得到MPC策略的滚动时域及预测步长对优化结果的影响并进行原理分析,最终验证所提方法的有效性和可行性。
1 基于MPC的风储联合发电系统
微网内风储联合发电系统的整体结构如图1所示,由风电系统、双层储能系统及双层MPC控制器组成。图中:PW为风电输出功率;PE1及PE2分别为上下层储能系统实际储能功率;PG为风电系统经储能系统处理后并入微网的功率。
上层储能系统采用大容量、大功率但响应速度较慢的储能单元;下层储能系统采用小容量、小功率但响应速度较快的储能单元。上层MPC处理结果为下层MPC处理提供状态变量。双层MPC控制器负责双层储能系统的运行控制和优化管理,以保证风储联合发电系统输出功率PG的稳定性。

图1 风储联合发电系统结构示意图
Fig.1 Structure of wind-storage combined power generation system
2 基于MPC的多时间尺度优化策略及建模
MPC由预测模型、滚动优化、反馈校正3个部分组成:①当前时刻根据风电的历史信息和未来输入,预测风电系统未来滚动周期内的输出功率;②根据目标函数和约束条件,得到滚动周期内储能系统的控制指令序列,并执行滚动周期内第1个滚动时刻的控制指令;③下一个滚动周期,结合上一个滚动时刻的控制指令以更新状态变量,并重复上述步骤。反馈校正使预测值的精度始终保持在一个比较高的水平。
2.1 风储系统双时间尺度MPC优化策略
风储联合发电系统的目的是使风储合力满足接入微网的条件。传统方法是使用一阶低通滤波器或设置合适的风电功率预测值接入微网,然后利用储能补充功率额。但这种方法可能造成储能的剩余容量及充放电功率不能满足实际情况的问题。
为了解决此类问题,提出风储系统双时间尺度MPC优化策略,其结构示意图如图2所示。Tup及Tdown分别为上层及下层滚动周期;Δtup及Δtdown分别为上层及下层滚动周期内的一个预测步长,同时也是储能指令控制时长。
图2中的上下层MPC滚动交互策略为:得到上层第1个预测步长的储能控制指令,将其作为状态变量求解下层滚动周期内的储能控制指令,并滚动优化下层MPC。下层MPC不断向后滚动推进,直到下层滚动周期涉及上层滚动周期第2个预测步长的预测数据(如图2中橘黄色部分所示)。此时,返回上层并进行上层MPC下一个滚动周期的滚动优化,得到新的上层储能控制指令作为状态变量继续进行下层储能的滚动优化。如此循环,直到完成整个优化过程。
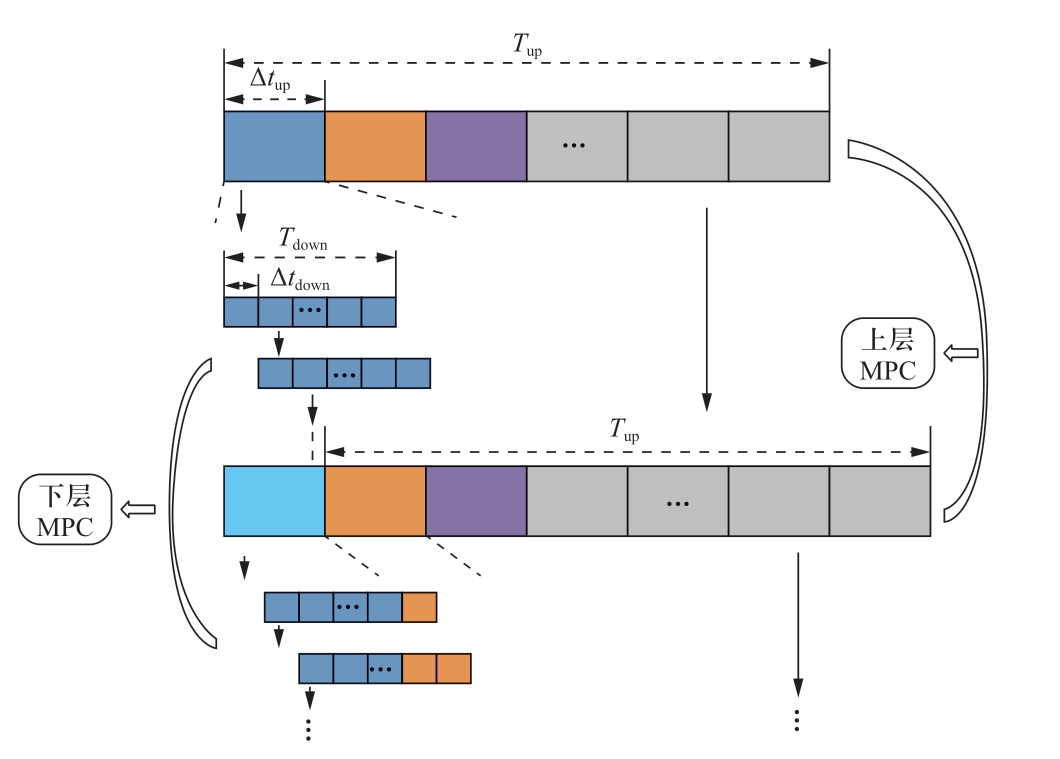
图2 基于MPC的双时间尺度储能优化模型
Fig.2 Structure of two time-scale energy storage optimization model based on MPC
2.2 上层滚动优化
上层滚动优化利用大功率慢速响应储能系统,其目的主要是降低风储系统输出功率的峰谷差,并控制大范围的风电功率波动。
2.2.1 目标函数
第T个上层滚动周期,目标函数由3部分组成:
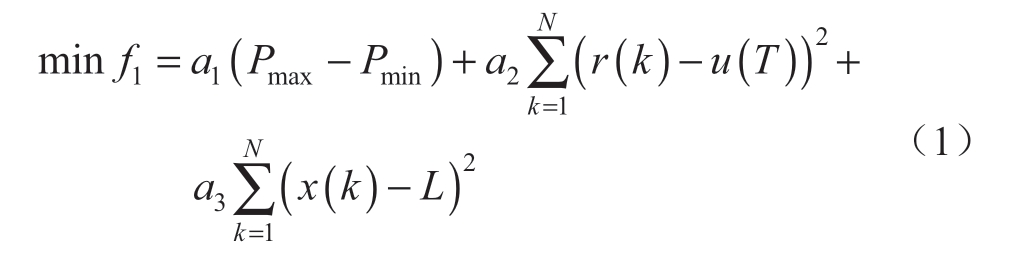
式中:a1、a2和a3分别是代表风储合力的最大峰谷差、风储合力方差和储能容量偏离程度对目标函数影响的系数;N为滚动周期内的步长数;Pmax和Pmin分别为风储合力的最大值和最小值;r(k)为第k个步长风储合力的均值;u(t)为周期内风储合力的均值;x(k)为第k个步长结束时的储能容量;L为储能最优容量。另外,步长内的值用采样值的平均值计算。
2.2.2 约束条件
1)上层储能系统充放电功率约束:
式中:PESS_1和Pmax_1分别代表上层储能系统的充放电功率和额定功率。
2)上层储能系统容量约束:
式中:SOCESS_1、SOCmin_1和SOCmax_1分别为上层储能系统的剩余容量占额定容量的比例、最小剩余容量占比和最大剩余容量占比。
3)上层储能系统与风电功率结合后的总出力上下限约束:
式中:Psum_1为上层储能系统和风电的联合出力;Pwn为风电系统额定功率。
4)上层相邻步长风储联合出力的差值约束:
式中:Det1、ΔPwind_1和ΔPESS_1分别代表上层功率最大差值系数、上层相邻两次步长的风电功率差值和储能出力差值。
2.3 下层滚动优化
下层滚动优化利用小功率快速响应储能系统,其目的主要是降低风储系统输出功率在短时间内的波动性。
2.3.1 目标函数
在第t个下层滚动周期,目标函数由3部分组成:
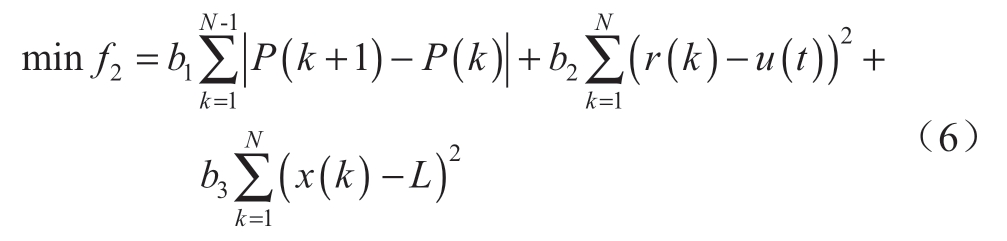
式中:b1、b2和b3分别代表滚动时域内风储合力的差值、方差和储能容量偏离程度对目标函数影响的系数;P为经双层储能优化过的风储合力。
2.3.2 约束条件
下层约束条件与上层储能系统的约束条件基本相同,包括下层储能充放电功率的约束、下层储能容量约束、下层储能与风电总出力的上下限约束以及下层相邻步长风储联合出力的差值约束。值得注意的是,下层相邻两次步长的风电功率差值为经上层储能出力调整后的差值。
3 算例仿真
以国外某装机容量为300 kW的风电系统为例,采用混合储能系统对其一天的出力进行优化。上层储能系统采用铅酸电池,下层储能系统采用超级蓄电池[20]。本文对不优化、只采用上层MPC优化和采用双层MPC优化的结果进行对比。算例仿真在MATLAB 2015a编译环境下,用粒子群优化算法进行求解。
粒子群算法是一种从随机解出发,追随当前搜索到的最优值来寻找全局最优解的一种算法,具有精度高、收敛快等优点。
3.1 仿真系统及参数
选取该风电系统典型情况下24 h风电功率数据,每10 min一个采样点。风电功率的基础预测误差为实际值的0.5%,每增加1个采样点,预测误差增加0.083%[28]。预测值从以实际值为μ、预测误差为σ的正态分布中抽样。
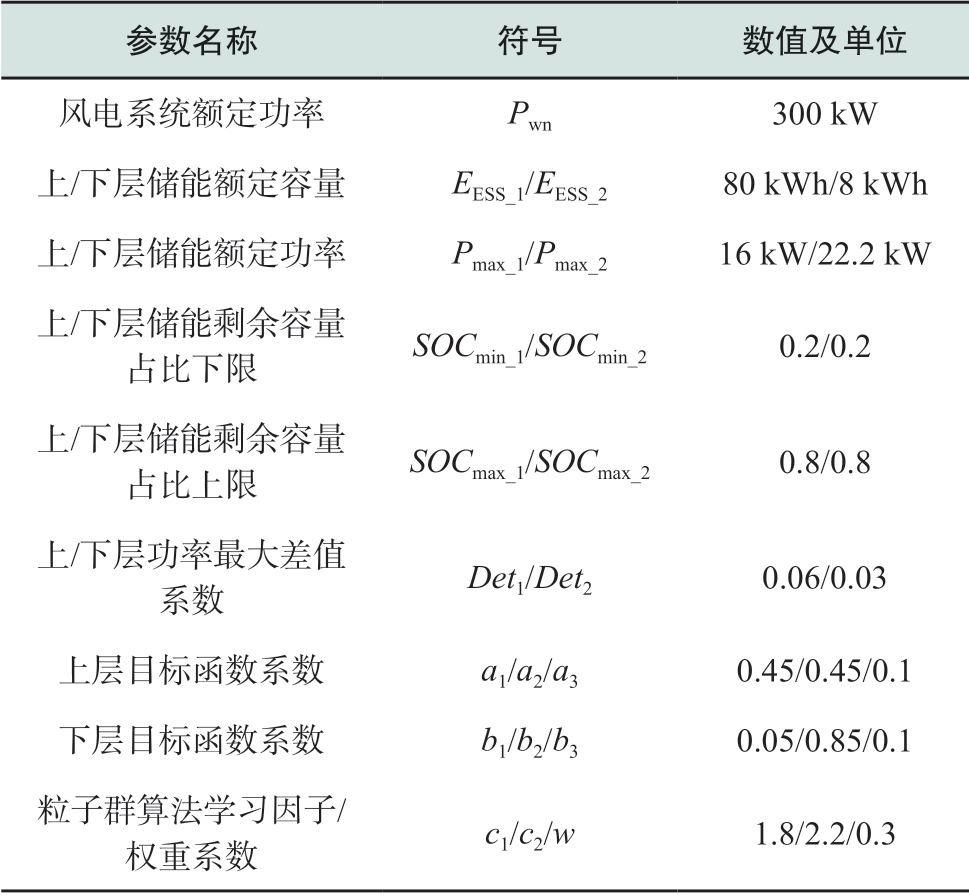
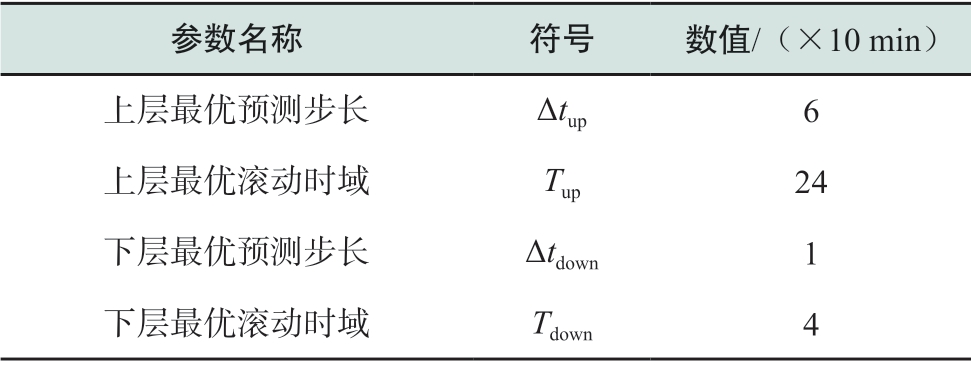
表1给出了仿真系统及参数,包括风电系统和双层储能相关参数、优化模型和优化算法相关参数。上下层储能的额定容量及额定功率是基于本风电系统的输出功率特性选择得到。
表1 仿真系统实验参数
Table1 Parameters of the simulation system
3.2 确定上层预测步长
原始风电功率曲线的峰谷特性及波动特性影响MPC参数的选择,不同预测步长及滚动时域对优化结果非常重要。
首先,确定上层预测步长的时间长度。在保持上层滚动时域变化不大的情况下,选择不同的预测步长进行算例分析,以体现预测步长对优化结果的影响。在对原始风电功率曲线的峰谷周期进行初步分析的基础上,选取上层预测步长为3~7的范围进行研究。实验参数如表2所示。
表2 上层预测步长实验参数
Table2 Parameters of upper-layer predicted step lengths
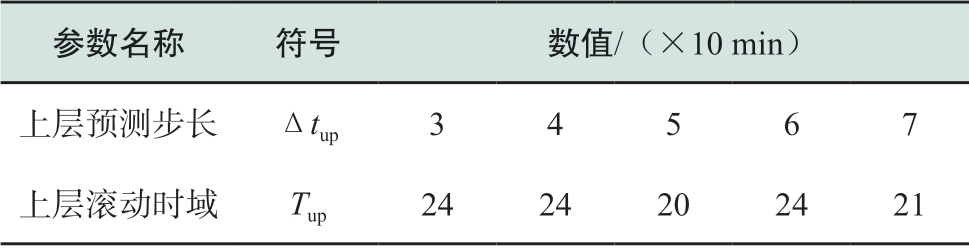
图3给出了原始风电功率曲线以及部分经不同上层预测步长储能优化的风电功率曲线的对比。
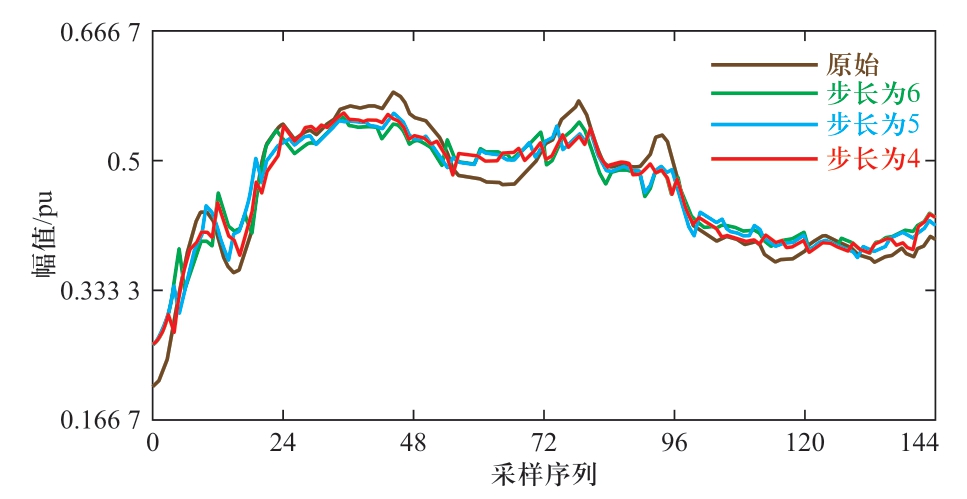
图3 经上层不同步长储能优化的风电功率
Fig.3 Wind power optimized by upper-layer energy storage of different predicted step lengths
使用离散傅里叶变换对以上的风电功率进行幅频特性分析,得到其幅频特性曲线。将经上层储能优化过后的风电功率与原始风电功率的幅频特性作对比,如图4所示。
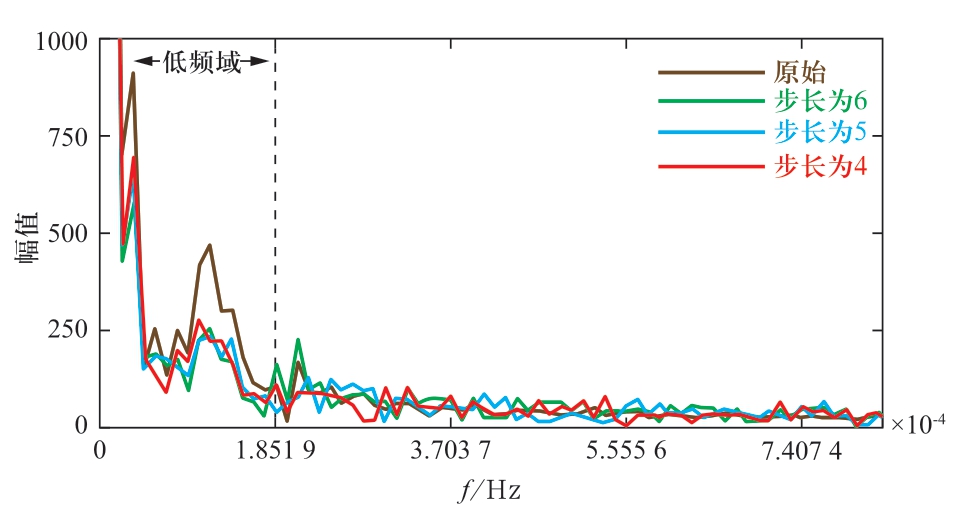
图4 经上层不同步长储能优化的幅频特性
Fig.4 Amplitude-frequency characteristic optimized by upperlayer energy storage of different predicted step lengths
上层储能系统主要调整风电功率在上层滚动时域内的峰谷差。根据图4,经上层储能优化后的风电功率幅频特性的幅值在低频域较原始幅频特性下降明显。
理论上,当储能系统容量取值足够大时,可以将频域幅值降低到一个很小的值,但需要较大的储能系统容量。本文是在确保储能容量能够满足约束的基础上进行的优化研究。表3的评价指标说明了上层储能策略对风电峰谷特性的改善效果。
表3 上层不同步长储能优化评价指标
Table3 Evaluation indicators of upper-layer energy storage optimization of different step lengths

由表3数据可知,步长为6时低频域幅值降低百分比最大;步长增大或减小,改善效果均降低。这是由于原始风电功率曲线的峰谷特性与步长为6的时间长度最为相符。步长太大会使局部峰谷特性得不到调整,步长太小也会降低整体调节效果。以上分析说明步长对于优化结果有重要影响,选择上层MPC的预测步长为6。
3.3 确定上层滚动时域
在上层预测步长不变的情况下,选择不同的滚动时域进行算例分析,以体现滚动时域对优化结果的影响。实验参数如表4所示。
表4 上层滚动时域实验参数
Table4 Parameters of upper-layer scrolling time domain experiment
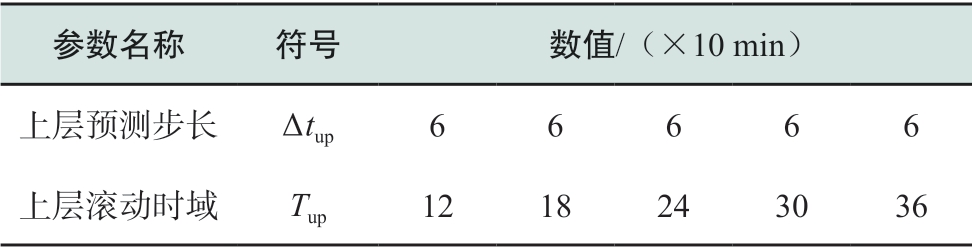
图5给出了原始风电功率曲线以及经不同上层滚动时域储能优化的风电功率曲线的优化结果。
使用离散傅里叶变换对以上的风电功率进行幅频特性分析,得到其幅频特性曲线。将经上层储能优化过后的风电功率与原始风电功率的幅频特性作对比,如图6所示。
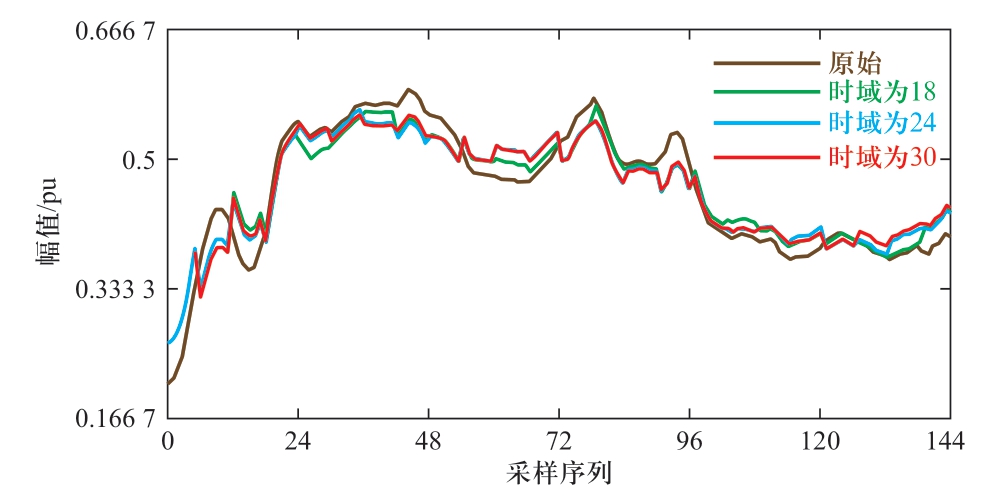
图5 经上层不同时域储能优化的风电功率
Fig.5 Wind power optimized by upper-layer energy storage of different time domains
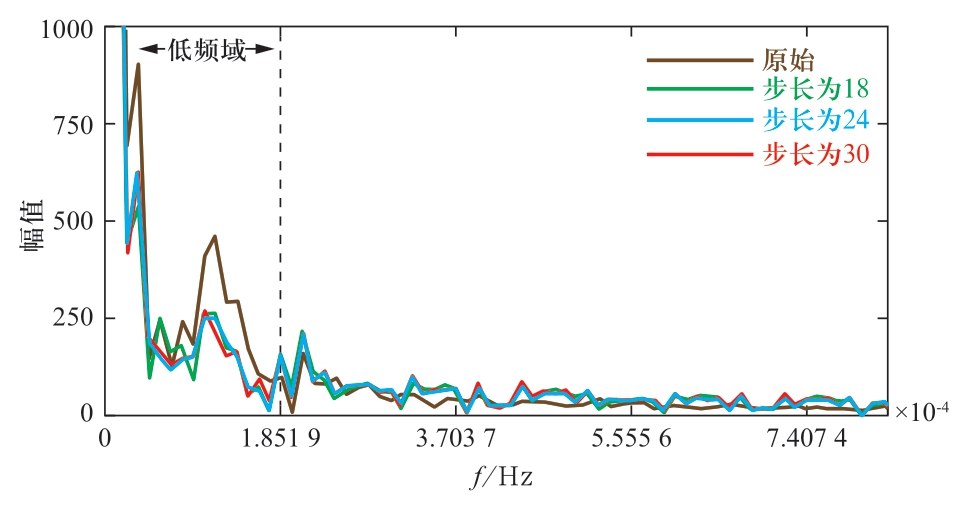
图6 经上层不同时域储能优化的幅频特性
Fig.6 Amplitude-frequency characteristic optimized by upperlayer energy storage of different time domains
根据图6,经上层储能优化后的风电功率的幅频特性在低频域较原始幅频特性下降明显,验证了其对于风电的峰谷特性有所改善。表5的评价指标说明了上层储能策略对风电峰谷特性的改善效果。
表5 上层不同时域储能优化评价指标
Table5 Evaluation indicators of upper-layer energy storage of different time domains

根据表5可知,滚动时域为24时低频域幅值降低百分比最大,滚动时域增加和减小,改善效果均降低。这是因为滚动时域太大,会使局部改善效果不够理想;滚动时域太小,会忽视整体特性对优化结果的影响。滚动时域长度的选择在一定程度上影响着优化结果,选择24作为上层MPC的滚动时域。
3.4 下层预测步长及滚动时域的确定
一般设定下层MPC预测步长和风电功率的采样周期相同,数值为1。在下层预测步长不变的情况下,选择不同的滚动时域进行算例分析,以体现滚动时域对优化结果的影响。实验参数如表6所示。
表6 下层滚动时域实验参数
Table6 Parameters of lower-layer scrolling time domain experiment
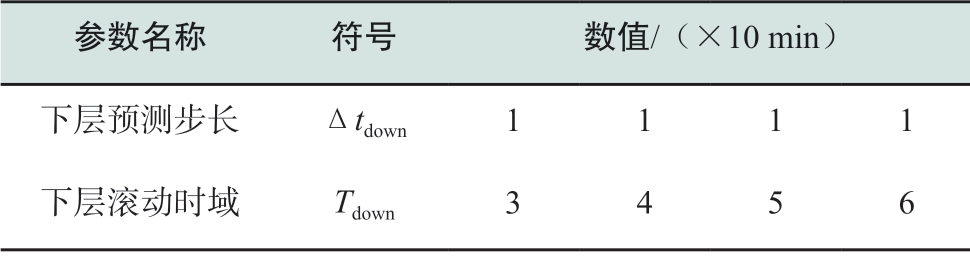
图7给出了原始风电功率曲线以及经不同下层滚动时域储能优化的风电功率曲线的对比。
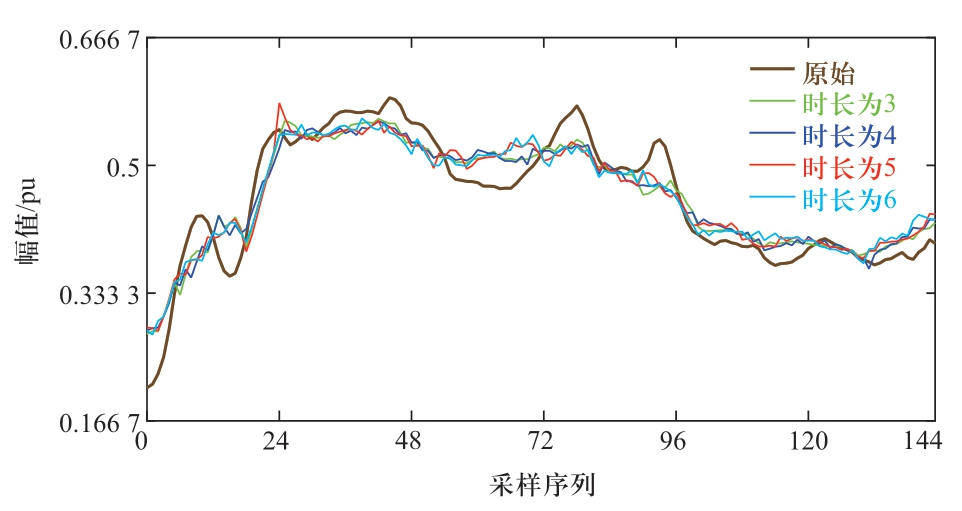
图7 经下层不同时域储能优化的风电功率
Fig.7 Wind power optimized by lower-layer energy storage of different time domains
使用离散傅里叶变换对以上的风电功率进行幅频特性分析,得到其幅频特性曲线。将经双层储能优化后的风电功率与原始风电功率的幅频特性作对比,如图8所示。
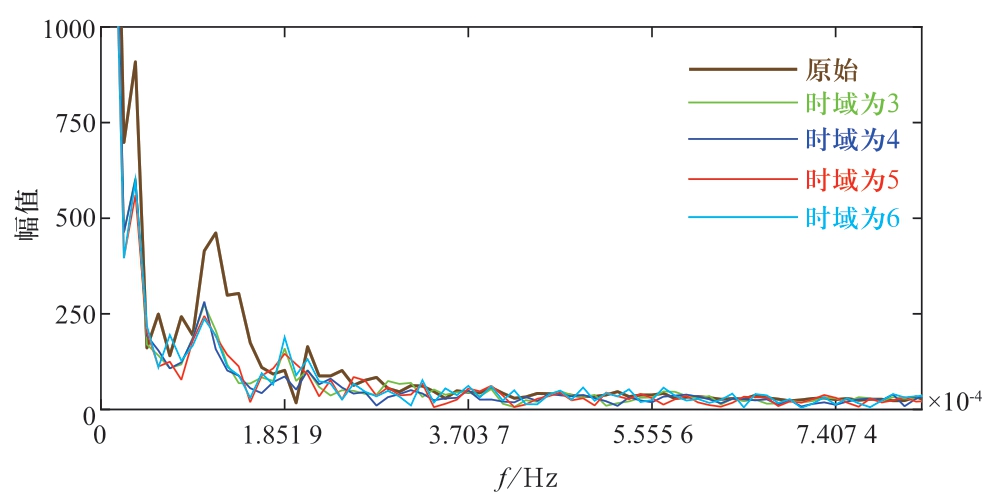
图8 经下层不同时域储能优化的幅频特性
Fig.8 Amplitude-frequency characteristic optimized by lowerlayer energy storage of different time domains
下层MPC策略主要降低风电功率在下层滚动时域内的波动性。由图8可以看出,经双层储能优化后的风电功率相比原始幅频特性在高频域产生了下降,说明其短时域内的波动特性明显更优,验证了其对于风电波动性的改善效果。
表7的评价指标说明了双层储能策略对风电峰谷差及波动性的改善效果。
表7 下层不同时域储能优化评价指标
Table7 Evaluation indicators of lower-layer energy storage of different time domains
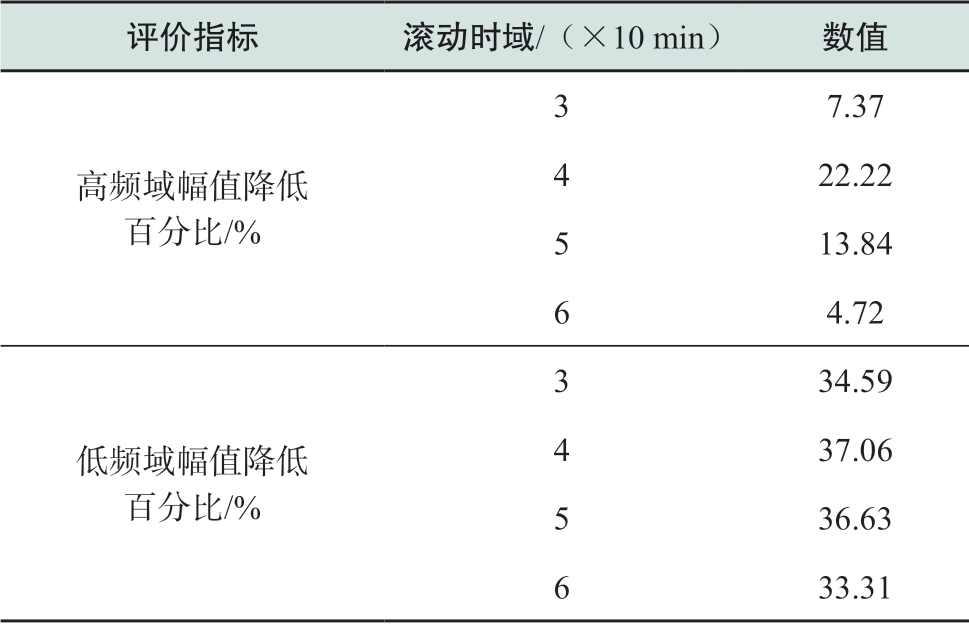
根据表7,在下层滚动时域为4时,高频域幅值降低百分比最大,并且在滚动时域增加或减小时,改善效果均降低,选择4作为下层MPC的滚动时域。
最后给出上下层储能的SOC变化趋势,如图9所示。
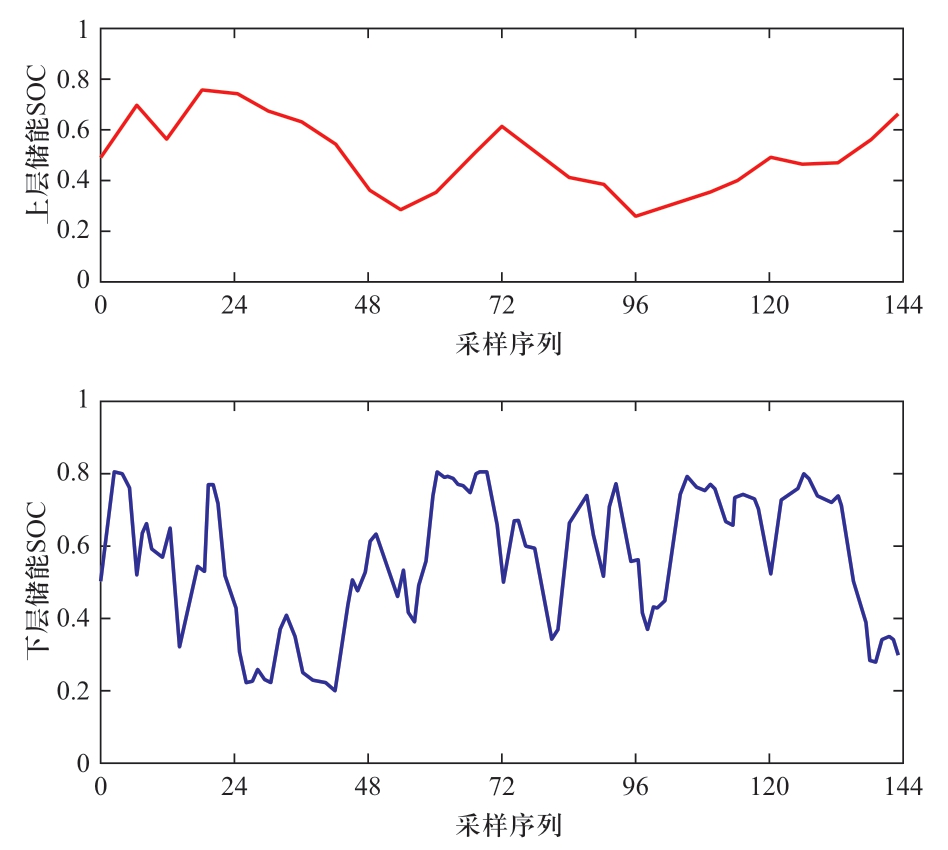
图9 储能SOC变化趋势
Fig.9 SOC for energy storage on typical day
可以看到,储能的初始SOC设置为0.5,随着时间的推进,SOC均运行在合理范围内。
3.5 结果
总结以上研究,实验结果如表8所示。
表8 实验结果
Table8 Results of the experiment
优化后的风电功率幅频特性相比原始特性的幅值分别在高频域下降了22.22%,在低频域下降了37.06%。仿真结果可以证明经过双层储能优化后,风电功率的幅频特性曲线相比原始幅频特性曲线有了一定程度的下降,表明风储联合系统输出功率具有更优的峰谷特性及波动性。
4 结论
本文针对风电输出功率的峰谷特性及波动性,为应对风电功率预测精度随时间尺度的增加而降低的问题,研究了基于预测控制的储能系统多时间尺度动态响应优化策略。该策略从上下两层储能系统的控制入手,结合离散傅里叶变换,得到适用于风储联合发电系统的双层MPC最优预测步长及滚动时域。针对不同算例,最优预测步长及滚动时域的数值或许不同,但均可采用本文提出的方法进行分析研究。最后验证了本方案能够在长时间尺度上降低风电功率的峰谷差,在短时间尺度上平稳风电功率的波动性。
为得到具有更高鲁棒性的研究结果,可以将考虑新能源在时间断面上的预测误差随机模型控制技术作为未来的研究方向。
参考文献
[1] NAGARAJAN A,AYYANAR R.Design and strategy for the deployment of energy storage systems in a distribution feeder with penetration of renewable resources[J].IEEE Transactions on Sustainable Energy,2015,6(3): 1085-1092.
[2] WANG Y,HU Q H,SRINIVASAN D,et al.Wind power curve modeling and wind power forecasting with inconsistent data[J].IEEE Transactions on Sustainable Energy,2019,10(1): 16-25.
[3] ZHAO H R,SUN H B,XUE Y S,et al.Optimal active power control of a wind farm equipped with energy storage system based on distributed model predictive control[J].IET Generation,Transmission & Distribution,2016,10(3): 669-677.
[4] 徐立中,易永辉,朱承治,等.考虑风电随机性的微网多时间尺度能量优化调度[J].电力系统保护与控制,2014,42(23):1-8.
XU Lizhong,YI Yonghui,ZHU Chengzhi,et al.Multitime scale optimal energy dispatch of microgrid considering stochastic wind power[J].Power System Protection and Control,2014,42(23): 1-8(in Chinese).
[5] 谢桦,滕晓斐,张艳杰,等.风/光/储微网规划经济性影响因素分析[J].电力系统自动化,2019,43(6):70-76.
XIE Hua,TENG Xiaofei,ZHANG Yanjie,et al.Analysis of economic influence factors in wind-photovoltaic-storage microgrid[J].Automation of Electric Power Systems,2019,43(6): 70-76(in Chinese).
[6] 李守东,董海鹰,张蕊萍,等.考虑风电消纳的电热联合系统多源协调优化运行[J].太阳能学报,2018,39(8):2217-2225.
LI Shoudong,DONG Haiying,ZHANG Ruiping,et al.Multi-source coordination and optimazation operation of combined heat and power system considering wind power consumption[J].Acta Energiae Solaris Sinica,2018,39(8): 2217-2225(in Chinese).
[7] 戴远航,陈磊,闵勇,等.风电场与含储热的热电联产联合运行的优化调度[J].中国电机工程学报,2017,37(12):3470-3479.
DAI Yuanhang,CHEN Lei,MIN Yong,et al.Optimal dispatch for joint operation of wind farm and combined heat and power plant with thermal energy storage[J].Proceedings of the CSEE,2017,37(12): 3470-3479(in Chinese).
[8] 夏沛,邓长虹,龙志君,等.含抽水蓄能机组的风电消纳鲁棒机组组合[J].电力系统自动化,2018,42(19):41-53.
XIA Pei,DENG Changhong,LONG Zhijun,et al.Robust unit commitment with pumped storage units for wind power accommodation[J].Automation of Electric Power Systems,2018,42(19): 41-53(in Chinese).
[9] 崔强,王秀丽,王维洲.考虑风电消纳能力的高载能用户错峰峰谷电价研究[J].电网技术,2015,39(4):946-952.
CUI Qiang,WANG Xiuli,WANG Weizhou.Stagger peak electricity price for heavy energy-consuming enterprises considering improvement of wind power accommodation[J].Power System Technology,2015,39(4): 946-952(in Chinese).
[10] CHOWDHURY M,RAO M,ZHAO Y,et al.Benefits of storage control for wind power producers in power markets[J].IEEE Transactions on Sustainable Energy,2016,7(4): 1492-1505.
[11] ZHANG F,MENG K,XU Z,et al.Battery ESS planning for wind smoothing via variable-interval reference modulation and self-adaptive SOC control strategy[J].IEEE Transactions on Sustainable Energy,2017,8(2): 695-707.
[12] 蔡霁霖,徐青山,袁晓冬,等.基于风电消纳时序场景的电池储能系统配置策略[J].高电压技术,2019,45(3):993-1001.
CAI Jilin,XU Qingshan,YUAN Xiaodong,et al.Configuration strategy of large-scale battery storage system orienting wind power consumption based on temporal scenarios[J].High Voltage Engineering,2019,45(3): 993-1001(in Chinese).
[13] 任建文,许英强,董圣孝.考虑储能参与的含高比例风电互联电力系统分散式调度模型[J].电网技术,2018,42(4):1079-1086.
REN Jianwen,XU Yingqiang,DONG Shengxiao.A decentralized scheduling model with energy storage participation for interconnected power system with high wind power penetration[J].Power System Technology,2018,42(4): 1079-1086(in Chinese).
[14] 吴玮坪,胡泽春,宋永华.结合随机规划和序贯蒙特卡洛模拟的风电场储能优化配置方法[J].电网技术,2018,42(4):1055-1062.
WU Weiping,HU Zechun,SONG Yonghua.Optimal sizing of energy storage system for wind farms combining stochastic programming and sequential Monte Carlo simulation[J].Power System Technology,2018,42(4): 1055-1062(in Chinese).
[15] 张鹏,张峰,梁军,等.采用小波包分解和模糊控制的风电机组储能优化配置[J].高电压技术,2019,45(2):609-617.
ZHANG Peng,ZHANG Feng,LIANG Jun,et al.Capacity optimization of hybrid energy storage system for wind farm using wavelet packet decomposition and fuzzy control[J].High Voltage Engineering,2019,45(2): 609-617(in Chinese).
[16] 娄素华,杨天蒙,吴耀武,等.含高渗透率风电的电力系统复合储能协调优化运行[J].电力系统自动化,2016,40(7):30-35.
LOU Suhua,YANG Tianmeng,WU Yaowu,et al.Coordinated optimal operation of hybrid energy storage in power system accommodated high penetration of wind power[J].Automation of Electric Power Systems,2016,40(7): 30-35(in Chinese).
[17] 李亚楠,王倩,宋文峰,等.混合储能系统平滑风电出力的变分模态分解-模糊控制策略[J].电力系统保护与控制,2019,47(7):58-65.
LI Yanan,WANG Qian,SONG Wenfeng,et al.Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs[J].Power System Protection and Control,2019,47(7): 58-65(in Chinese).
[18] 吴杰,丁明.采用自适应小波包分解的混合储能平抑风电波动控制策略[J].电力系统自动化,2017,41(3):7-12.
WU Jie,DING Ming.Wind power fluctuation smoothing strategy of hybrid energy storage system using self-adaptive wavelet packet decomposition[J].Automation of Electric Power Systems,2017,41(3): 7-12(in Chinese).
[19] DI GIORGIO A,LIBERATI F,LANNA A,et al.Model predictive control of energy storage systems for power tracking and shaving in distribution grids[J].IEEE Transactions on Sustainable Energy,2017,8(2): 496-504.
[20] WANG T,KAMATH H,WILLARD S.Control and optimization of grid-tied photovoltaic storage systems using model predictive control[J].IEEE Transactions on Smart Grid,2014,5(2): 1010-1017.
[21] PAHASA J,NGAMROO I.Coordinated PHEV,PV,and ESS for microgrid frequency regulation using centralized model predictive control considering variation of PHEV number[J].IEEE Access,2018,6: 69151-69161.
[22] KHALID M,SAVKIN A V.A model predictive control approach to the problem of wind power smoothing with controlled battery storage[J].Renewable Energy,2010,35(7): 1520-1526.
[23] 董雷,陈卉,蒲天骄,等.基于模型预测控制的主动配电网多时间尺度动态优化调度[J].中国电机工程学报,2016,36(17):4609-4617.
DONG Lei,CHEN Hui,PU Tianjiao,et al.Multi-time scale dynamic optimal dispatch in active distribution network based on model predictive control[J].Proceedings of the CSEE,2016,36(17): 4609-4617(in Chinese).
[24] 蔡宇,林今,宋永华,等.基于模型预测控制的主动配电网电压控制[J].电工技术学报,2015,30(23):42-49.
CAI Yu,LIN Jin,SONG Yonghua,et al.Voltage control strategy in active distribution network based on model predictive control[J].Transactions of China Electrotechnical Society,2015,30(23): 42-49(in Chinese).
[25] 杨德友,温佳鑫,陈家荣,等.用于提高风电场可调度性的储能系统预测控制策略[J].高电压技术,2017,43(3):1043-1048.
YANG Deyou,WEN Jiaxin,Kevin Chan,et al.Smoothing and dispatching the output of wind/battery energy storage hybrid system via model prediction control[J].High Voltage Engineering,2017,43(3): 1043-1048(in Chinese).
[26] 肖斐,艾芊.基于模型预测控制的微电网多时间尺度需求响应资源优化调度[J].电力自动化设备,2018,38(5):184-190.
XIAO Fei,AI Qian.Multiple time-scale optimal dispatch of demand response resource for microgrid based on model predictive control[J].Electric Power Automation Equipment,2018,38(5): 184-190(in Chinese).
[27] 孙玉树,唐西胜,孙晓哲,等.风电波动平抑的储能容量配置方法研究[J].中国电机工程学报,2017,37(增刊1):88-97.
SUN Yushu,TANG Xisheng,SUN Xiaozhe,et al.Research on energy storage capacity allocation method for smoothing wind power fluctuations[J].Proceedings of the CSEE,2017,37(Supplement 1): 88-97(in Chinese).
[28] BAKER K,HUG G,LI X.Energy storage sizing taking into account forecast uncertainties and receding horizon operation[J].IEEE Transactions on Sustainable Energy,2017,8(1): 331-340.
Multi-time Scale Dynamic Response Optimization of Energy Storage System Based on Predictive Control
WU Chuanshen,LIU Yu,GAO Shan*,ZOU Ziqing,HUANG Xueliang
(Southeast University,Nanjing 210000,Jiangsu Province,China)
Abstract: The inherent randomness of wind power makes it difficult to predict the amount of wind that will be stored in a turbine over a long span of time.The prediction error increases if the prediction time is extended,resulting in a large deviation between the power output after the application of the control strategy used to deal with wind power changes and the actual demand.In order to effectively cope with the dynamic randomness of wind power,this paper applies a hybrid energy storage system composed of energy storage units with different response capabilities and capacities.It proposes a hybrid energy storage hierarchical model predictive control(MPC)optimization strategy based on multi-time hierarchy and MPC,to achieve precise control of wind power and storage.Based on the periodic prediction of wind power,a layered dynamic response optimization model of energy storage is constructed.The wind power is transferred over a long time scale by an upper layer by using an energy storage unit with high power and slow response.The lower layer uses an energy storage unit with low power and fast response to smoothen the wind power fluctuations over a short time scale,and the results of the upper layer optimization are taken as the state variables of the lower layer optimization.Through the layered model predictive control,the predictive information of the wind power cycle at different time levels is updated continuously,and the optimal control of energy storage among layers can also be effectively coordinated.For the windstorage-combined power generation system in the micro-grid,the optimal parameters are obtained by changing the rolling time domain and step size of the layered MPC.The simulation results confirm that the strategy can dynamically respond to wind power changes and effectively reduce the peak-to-valley characteristics and volatility of the output.
Keywords: wind power; energy storage system; multitime scale; model predictive control; dynamic response optimization
作者简介:

吴传申
吴传申(1993),男,博士研究生,研究方向为电力系统运行与控制、分布式发电协调控制,E-mail:chuanshen160@gmail.com。
刘宇(1990),男,讲师,研究方向为电力系统运行规划、新能源并网、主动配电网等,E-mail:liuyu_seu@126.com。
高山(1973),男,副教授,博士生导师,主要研究方向为电力系统运行与控制、分布式发电协调控制、智能调度、主动配电网等。通信作者,E-mail:shangao@seu.edu.cn。
(责任编辑 张宇)
