0 引言
近年来,频发的极端灾害事件给电力系统稳定运行带来了严重的影响,如2008年中国南方冰灾、2011年东日本地震、2012年美国桑迪飓风等自然灾害以及2015年乌克兰大停电等人为攻击事件均引起大范围、长时间的停电,造成了巨大的经济损失。提升电网在极端事件下的生存及恢复能力、建设弹性电网成为一项引起广泛关注的课题。增强电网弹性的措施主要可以归为两个方面:硬件强化规划和优化运行策略[1]。硬件强化规划包括提升元器件防灾等级、升高变电站、植被管理、将输电线路埋入地下等;优化运行策略主要关注应用智能电网技术、自动化设备和恢复策略帮助电网在灾害发生时有效响应、适应和灾后快速恢复[2]。
分布式电源、微网、主动配电网等技术的发展为建设弹性电网提供了更多思路。文献[3]提出基于分布式电源和远动开关的配网灾后重构模型,在配电网发生故障后,将非故障区域重构分区形成多个微网,依靠分布式电源继续为负荷供电。文献[4]提出移动应急发电车的部署与实时调度双层优化模型,灾后通过应急电源接入形成微网,保障区域负荷的电力供应。文献[5]通过分层管理微网内能源资源,最大限度减小灾后停电损失。文献[6]提出考虑分布式电源和电动汽车的配电网重构模型,基于对开关状态进行编码并制定编码规则保证网络的连通性及辐射状结构,通过改进的生物地理优化算法求解模型。文献[7]提出了配电网灾后故障抢修与依靠分布式电源重构恢复的协调优化策略,将故障抢修与负荷恢复分别建立为外层、内层模型,应用启发式算法求解,通过预先设置的辐射状拓扑集合对重构拓扑进行约束。
对分布式电源进行优化配置,是使其更有效地参与负荷保障和恢复的前提。文献[8]提出了一种微网分布式电源配置与线路强化模型,基于三层鲁棒算法,考虑多时段最严重的灾害攻击与运行调度进行优化规划。该模型未对电源供电路径以及可能出现的拓扑环路加以限制。文献[9]提出配网分布式电源的鲁棒配置模型,建立考虑灾害时空特性的故障不确定集,针对最严重的灾害场景配置电源,在灾后依靠分布式电源为电源节点及其子点供电。文献[10]建立随机规划模型在飓风前配置分布式电源等发电设备,灾后建立辐射状恢复路径恢复重要负荷。以上分布式电源配置方法没有考虑灾后配网拓扑重构以及依靠分布式电源形成微网为更大区域的负荷供电,限制了分布式电源灾后发挥的负荷保障作用。
此外,在高可再生能源渗透背景下,考虑风、光资源出力间歇性和波动性的影响,以及可控机组和可再生能源机组在恢复负荷阶段的协调控制对提升电网弹性和灵活性具有重要意义。文献[11]提出一种基于主从控制的灾后微网分区方法,依靠可控分布式电源和可再生能源机组形成微网参与负荷恢复,并在重构阶段提出了给定灾害下的孤岛子图识别方法。
本文提出了一种可再生能源分布式电源配置的鲁棒优化模型。考虑灾后配网拓扑重构、微网分区等恢复策略,针对故障不确定集下最严重的故障场景,在规划阶段配置可再生能源电源,提升配电网弹性。同时,为考虑可再生能源出力不确定性的影响,构建一系列可再生能源出力场景,以各场景下的灾后切负荷期望最小为目标进行优化配置。本文的主要创新点为:①提出了提升配电网弹性和灵活性的可再生能源机组配置方法,并将优化问题建立为考虑随机出力场景及故障不确定性的鲁棒优化模型;②在规划阶段考虑了灾后优化运行与网络重构等恢复措施,通过可控机组和可再生能源机组形成微网恢复负荷;③应用NCCG算法将模型解耦为上层问题、下层主问题和下层子问题三层进行迭代求解,在求解最严重攻击策略时,建立攻击线路与孤岛子图的关系解决了可再生能源机组运行状态在攻击策略确定前无法判断的难点。
1 可再生能源出力场景构建
本文以风电机组为例,对分布式可再生能源出力进行建模,生成出力场景并削减获取典型场景。
1.1 可再生能源出力模型
针对风速不确定性,采用Weibull分布近似刻画风速概率分布[12]:
式中:fW(v)代表风速的概率密度函数;k、c为形状参数和尺度参数,v代表风速。
风速与出力功率之间的关系可以写为:
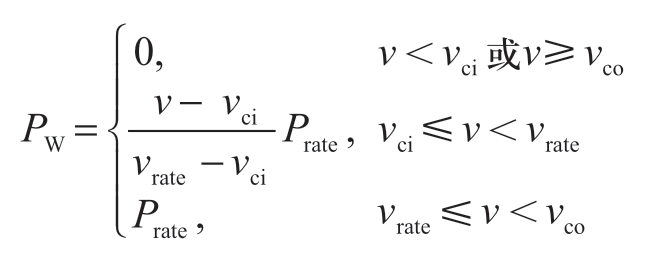
式中:v代表风速;Prate为风力发电机额定容量;vci、vrate、vco分别代表切入风速、额定风速以及切出风速[9]。
1.2 可再生能源出力场景生成与削减
对风速采用拉丁超立方抽样法进行分层抽样[13],生成风速序列场景,并进行场景削减。
场景削减算法目的在于确定一个初始场景集的子集,并为该子集重新分配概率,使子集的概率分布Q与初始场景集的概率分布P之间的某种概率距离最短,该距离一般使用康托洛维奇(Kantorovch)距离DK:
式中:ξi为概率分布P中的场景,pi为其发生的概率;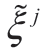 为概率分布Q中的场景,qj为其发生的概率;S为概率分布P的场景数;
为概率分布Q中的场景,qj为其发生的概率;S为概率分布P的场景数; 为概率分布Q的场景数;
为概率分布Q的场景数;![]() 表示场景ξi、
表示场景ξi、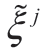 之间的距离。该问题可以使用前向选择法、后向选择法等求解[14]。
之间的距离。该问题可以使用前向选择法、后向选择法等求解[14]。
2 模型建立
极端事件(自然灾害或人为攻击)对配电网影响缺乏相应的历史数据、专家经验及物理结构分析模型,难以得到准确的概率函数来描述灾害与元器件状态的关系,采用随机规划生成电网故障场景具有较大的难度,因此本文采用鲁棒规划的方法,考虑配电网可能遭受的最严重攻击制定可再生能源电源的配置方案。同时,由于可再生能源出力已有较为完善的概率模型和场景生成、削减方法,本文通过构建一系列出力场景描述其不确定性。将鲁棒优化模型建立为防御—攻击—防御三层优化框架[15],对于给定的分布式电源配置方案,攻击者考虑配电网潮流调整、网络重构等灾后优化运行措施,制定最严重的灾害攻击策略,防御者制定最优分布式电源配置方案,使其在遭受相应的最严重攻击下切负荷损失期望最小。建立优化模型的目标函数为:
式中:Chj为在节点j配置分布式可再生能源电源的费用;hj表示是否在节点j配置电源的二进制决策变量,取1时表示配置;h表示分布式可再生能源电源配置的决策变量向量;u表示攻击策略变量向量;z表示配网潮流优化变量向量;r和c分别表示拓扑重构的连续和离散变量向量;s和S分别表示可再生能源出力场景和场景集合;ρs表示场景s的概率;t和T分别表示优化的时间段及时段集合,优化时长可以根据预测故障修复所需时间进行设定;V表示节点集合;Psshed,j,t表示场景s下节点j在时段t的负荷有功功率切除值。
2.1 攻击与线路状态约束
假设线路受到攻击后在优化时间段内将一直处于故障断开状态,攻击与线路状态约束为:
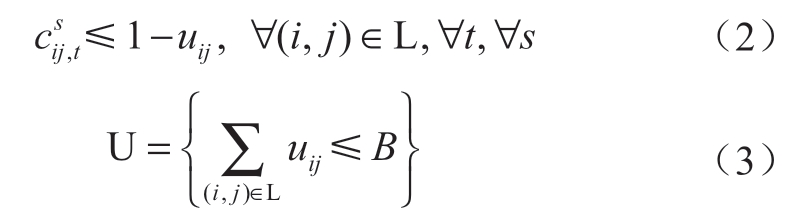
式中:uij为表示线路(i,j)是否受到攻击的二进制变量,取1时为受到攻击;csij,t为表示线路断开与闭合状态的二进制变量,取0表示线路为断开状态,否则为闭合状态;L为配网线路的集合。式(2)表示若线路未受攻击,线路状态csij,t可以自由控制取0或1,若线路受到攻击,线路状态csij,t只能为0。式(3)中,B为最大攻击线路数的攻击预算,U表示攻击不确定集。
2.2 潮流约束
本文采用线性化配网潮流模型建立潮流约束,如图1所示,对线路潮流预先设定一个正方向,位于节点j流入方向的节点定义为j的父节点,π(j)表示父节点的集合;反之为子节点,其集合用δ(j)表示。若实际功率流向与正方向相反,潮流视为负值。
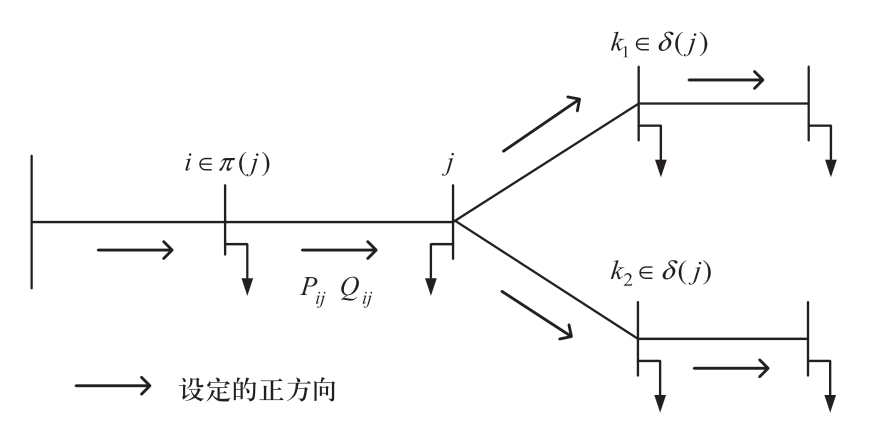
图1 配网潮流示意图
Fig.1 Schematic diagram of distribution system power flow
潮流约束如下:
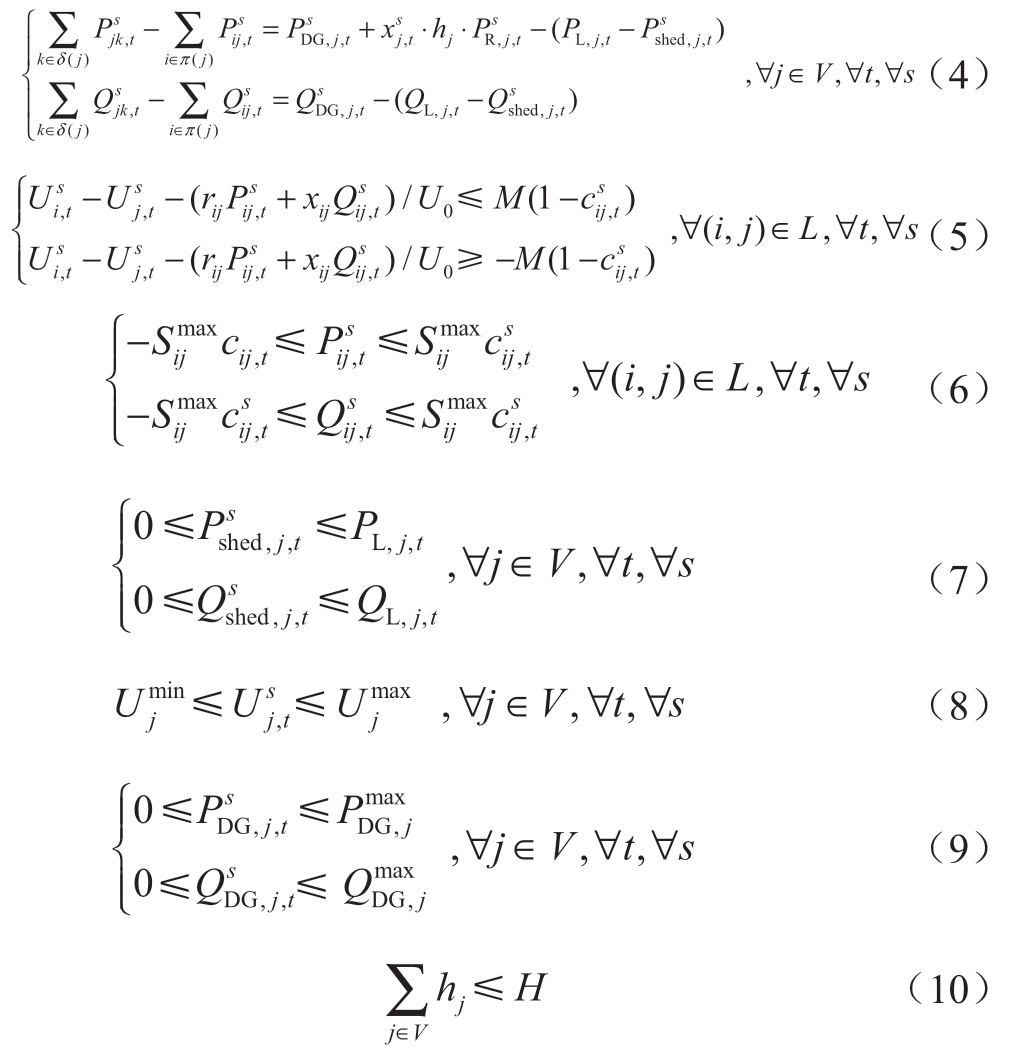
式(4)为功率平衡约束,Psij,t、Qsij,t表示流经线路(i,j)的有功、无功功率;PDsG,j,t、QsDG,j,t为节点j的可控分布式机组出力;参数PRs,j,t为场景s中可再生能源有功出力,由于配网地理区域通常较小,在同一场景中,假设所有可再生能源机组具有相同出力曲线;xsj,t为节点是否属于孤岛子图的二进制变量,取0时表示节点j属于孤岛子图,此时可再生能源机组j不出力,孤岛子图在2.3节中进行介绍;PL,j,t、Psshed,j,t分别为节点j的有功负荷需求以及切除功率,QL,j,t、Qsshed,j,t分别为无功负荷需求以及切除功率。式(5)建立相邻节点间电压大小关系,其中Usj,t为节点j的电压大小,rij和xij分别为线路(i,j)的电阻和电抗,U0为额定电压;M为一个大数。式(6)为线路容量约束,其中, 表示线路最大允许功率。式(7)为负荷切除约束。式(8)为节点电压大小上下限约束。式(9)表示节点j的可控分布式电源出力上下限,其中
表示线路最大允许功率。式(7)为负荷切除约束。式(8)为节点电压大小上下限约束。式(9)表示节点j的可控分布式电源出力上下限,其中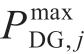 、
、 分别表示分布式电源最大有功、无功容量,若节点j与变电站相连,变电站容量计入有功出力上限。式(10)为配置分布式可再生能源电源的规划预算,即最大配置数量不应超过H。
分别表示分布式电源最大有功、无功容量,若节点j与变电站相连,变电站容量计入有功出力上限。式(10)为配置分布式可再生能源电源的规划预算,即最大配置数量不应超过H。
2.3 拓扑约束
在灾后恢复阶段,配电网依靠分布式电源通过控制线路开关和联络线开关重构为多个微电网。假设微电网采用主从控制方式,各微网内由一个可控分布式电源提供电压和频率参考,可再生能源机组控制功率[11]。在重构过程中微网需满足辐射状拓扑结构,约束为:
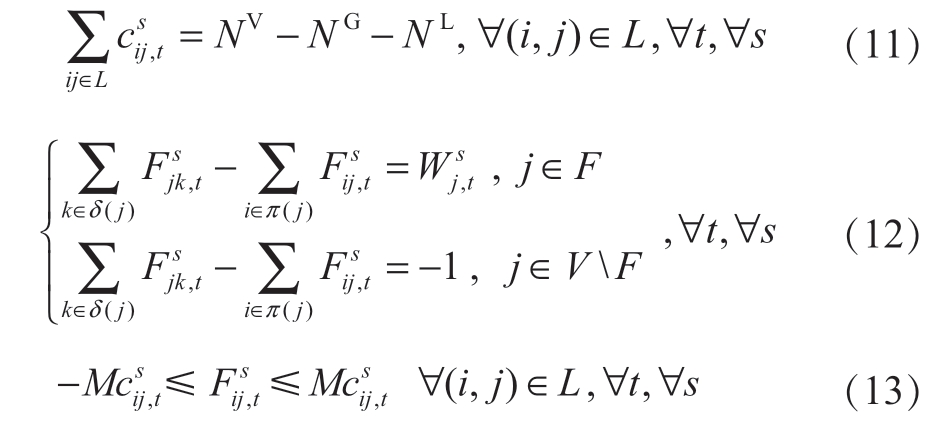
配网系统满足辐射状拓扑结构的充分必要条件为:①正常运行线路数量等于节点数与拓扑中子图(sub-graph)数之差;②每个子图的连通性得到满足[16]。式(11)表示正常运行的线路数量等于总节点数NV减可控分布式电源数NG及孤岛子图数NL,即充分必要条件1。孤岛子图指没有与可控分布式电源或变电站连通,仅由负荷节点和可再生能源机组节点组成的子图,对于一次给定攻击,孤岛子图数量NL及包含节点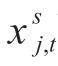 可由如下方法确定[11]:闭合所有非故障线路及联络线开关,确定与可控分布式电源或变电站不连通的子图数量,如图2所示,在该示例中,灾后有2个子图为孤岛子图,无法形成主从控制模式下的有源微网,在故障修复前将处于失负荷状态。
可由如下方法确定[11]:闭合所有非故障线路及联络线开关,确定与可控分布式电源或变电站不连通的子图数量,如图2所示,在该示例中,灾后有2个子图为孤岛子图,无法形成主从控制模式下的有源微网,在故障修复前将处于失负荷状态。
在求最严重攻击策略时,由于攻击决策为变量,在攻击确定前无法确定孤岛状态,进而无法判断可再生能源机组是否在运行状态。可结合式(2)和式(14)、(15)建立孤岛子图与攻击线路的关系:
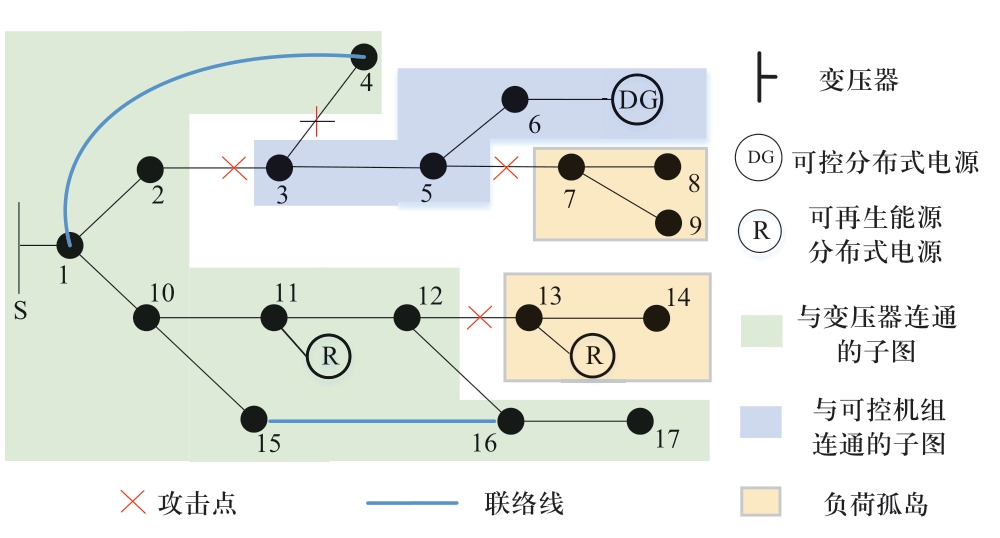
图2 识别孤岛示意图
Fig.2 Identification for load island
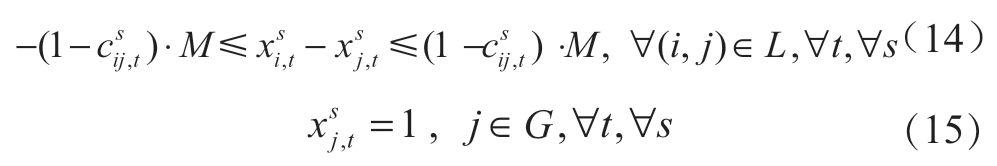
式(14)表示若线路(i,j)处于闭合状态(csij,t=1),节点i和节点j在是否属于孤岛子图上保持一致![]() ,若线路断开,约束被松弛。式(15)中,G表示可控分布式电源和变电站节点的集合,这些节点在任何攻击下都不属于孤岛子图,即xsj,t=1。
,若线路断开,约束被松弛。式(15)中,G表示可控分布式电源和变电站节点的集合,这些节点在任何攻击下都不属于孤岛子图,即xsj,t=1。
式(12)、(13)通过构造虚拟潮流保障各子图连通性[13],即充分必要条件2。其中,Fsij,t表示线路流通的虚拟功率;F表示可控分布式电源和变压器节点以及在各孤岛中分别选择一个节点所组成的节点集合,例如在图2中,集合F可以为{1,6,7,13}。对属于F的节点设置虚拟电源Wjs,t,其他节点设置虚拟负荷-1,式(12)表示在各子图中,虚拟负荷都能受到虚拟电源的功率供应,即各子图是连通的。式(13)表示若线路(i,j)处于断开状态,虚拟功率将不能流通。
3 模型求解
本文采用嵌套列约束生成算法求解鲁棒优化模型[17]。将模型分解为上层问题和下层问题,下层问题求解给定可再生能源机组配置方案后的最严重攻击策略,并在每次迭代时将攻击策略返回到上层问题中,上层问题基于一系列攻击策略组成的故障不确定集,求解最优可再生能源机组配置方案。由于配网重构模型含有整数变量,不能直接对偶求解,下层问题本身仍然是一个双层鲁棒问题,即求解一个最严重攻击策略,使其在最优重构措施下造成的切负荷期望最大。因此将下层问题进一步分解为下层主问题和下层子问题,下层子问题在给定攻击策略后求解最优拓扑重构措施,并在每次迭代时将重构结果返回下层主问题,下层主问题基于一系列重构拓扑的集合求解最严重攻击策略。
为了简化变量表示,定义所有潮流相关的变量![]() 组成向量z,可再生能源机组配置决策变量(hj)组成变量向量h,攻击决策变量(uij)组成变量向量u,拓扑重构相关的连续变量(Fsij,t,Wsj,t)组成向量r,拓扑重构相关的离散变量(csij,t)组成向量c,约束(4)-(13)用向量关系式A1h+B1z+C1c+D1u+E1r≥F1表示,约束(4)-(9)用向量关系式A2h+B2z+C2c≥F2表示。
组成向量z,可再生能源机组配置决策变量(hj)组成变量向量h,攻击决策变量(uij)组成变量向量u,拓扑重构相关的连续变量(Fsij,t,Wsj,t)组成向量r,拓扑重构相关的离散变量(csij,t)组成向量c,约束(4)-(13)用向量关系式A1h+B1z+C1c+D1u+E1r≥F1表示,约束(4)-(9)用向量关系式A2h+B2z+C2c≥F2表示。
3.1 上层问题
上层问题在给定的攻击策略集合下优化可再生能源电源配置方案,其数学表达式为:
定义辅助变量α,原问题转化为如下形式:
目标函数
约束条件
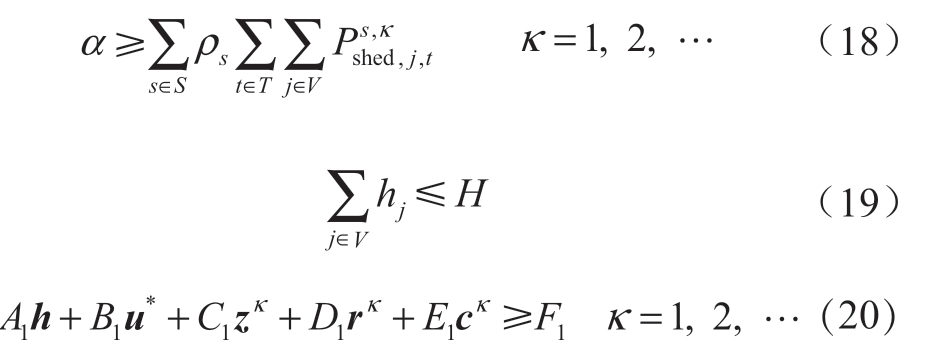
符号 * 表示相应的变量为给定值(由前一次迭代得到),κ为当前外层迭代次数。上层问题是原问题的一个松弛问题,因此求得的切负荷值为原问题提供下界。
3.2 下层问题
下层问题在给定的可再生能源机组配置方案下寻找最严重的攻击策略,使灾后期望切负荷损失最大,其数学表达式为:
在重构拓扑给定,即变量r和c为定值的情况下,下层问题的最小化问题可以通过对偶转化为最大化问题,从而直接求解。因此将下层问题进一步分解为下层主问题和下层子问题。
3.2.1 下层主问题
下层主问题在给定的拓扑重构下,求解最严重攻击策略:![]()
令η表示z关于约束(4)-(9)的对偶变量向量,Φ(h*)表示η的可行域,根据对偶原理(duality theory),内部的最小化问题可以转化为其对偶最大化问题:![]()
定义辅助变量β,下层主问题最终形式为:目标函数
约束条件
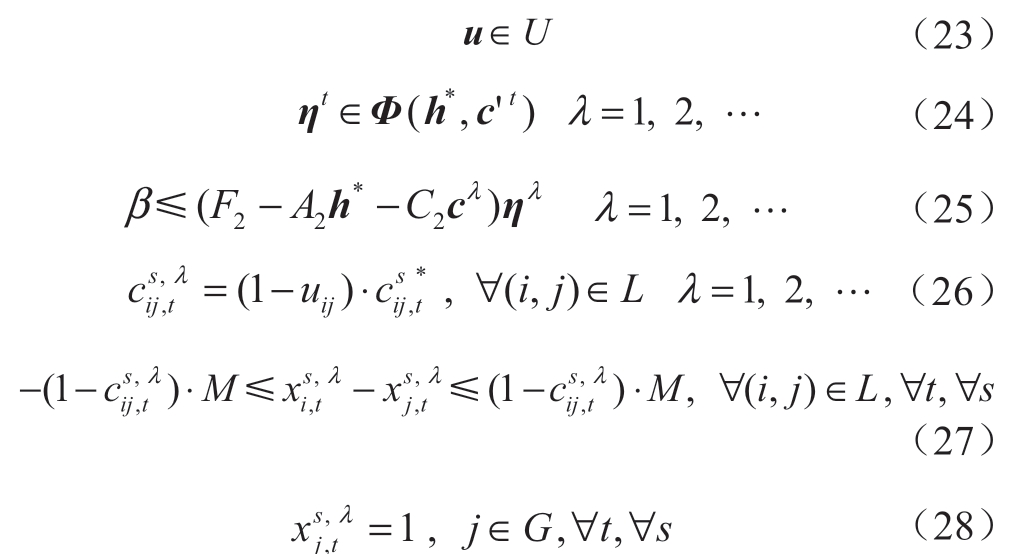
其中,λ为当前内层问题迭代次数;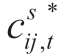 表示前次迭代中的下层子问题返回的线路断开与闭合状态,即给定的拓扑重构结果。式(26)表示在给定拓扑下,若线路未受到攻击(1-uij=1),则该线路和给定拓扑保持一致,若线路受到攻击,线路为断开状态。式(27)、(28)为式(14)、(15)的迭代形式。对偶后的非线性项可通过大M法进行线性化。
表示前次迭代中的下层子问题返回的线路断开与闭合状态,即给定的拓扑重构结果。式(26)表示在给定拓扑下,若线路未受到攻击(1-uij=1),则该线路和给定拓扑保持一致,若线路受到攻击,线路为断开状态。式(27)、(28)为式(14)、(15)的迭代形式。对偶后的非线性项可通过大M法进行线性化。
3.2.2 下层子问题
下层子问题在给定下层主问题求得的攻击策略后,优化潮流和拓扑使期望切负荷值最小,目标函数为:
约束条件为:
下层子问题的拓扑重构结果会返回到下次迭代的下层主问题中,当下层主问题和下层子问题收敛时,表示求得的攻击策略能够在最优拓扑重构措施下最大化切负荷损失。下层问题是在给定线路加固方案下求解最严重攻击策略,因此得到的切负荷值为原问题提供上界。
3.3 算法流程
嵌套列约束生成算法流程如图3所示。

图3 算法流程图
Fig.3 Implementation flowchart
4 算例分析
4.1 算例介绍

图4 改进的37节点系统图
Fig.4 Modified IEEE 37-node system
本文采用改进的IEEE 37节点系统[18]进行模型的求解分析。如图4所示,3个可控分布式电源预先配置在节点709、711、744,容量均为100 kW,节点725、731,节点731、741,节点728、735各有一条联络线相连,常态处于断开状态,节点799连接变电站,容量为0.5 MVA,各节点允许电压大小为额定电压的0.9~1.1,负荷数据参考自文献[3],系统总负荷为 981.58 kW+544.02 kvar,每时段设为1 h,优化总时段数为6(t=1,…,6),配置的可再生能源机组最大有功出力为150 kW,构建的5个可再生能源出力场景如图5所示。

图5 可再生能源出力场景
Fig.5 Renewable energy output scenarios
4.2 不同规划与攻击预算下优化结果比较
本节对几种不同可再生能源机组数量预算(H)以及最大攻击线路数(B)下的配置结果进行对比分析,配置结果及对应最严重攻击下的场景切负荷均值如表1所示。
表1 可再生能源配置结果及切负荷值
Table1 Renewable energy DG placement and curtailed load

通过对不同攻击预算下的配置结果进行对比,可以看出节点734、737等配置分布式电源的频率较高,这些节点可以视为关键节点。由于系统右上部分仅通过线路702-713以及联络线725-731与主干部分相连,当攻击线路数超过2时,可以切断右上部分与可控机组的连通,配置在此部分的可再生能源机组缺少可控机组对频率和电压的控制从而无法运行,因此可再生能源机组更适合配置在左下部分以应对最严重的攻击方式。针对左上部分与电源连通度不足的问题,可以结合增设联络线、加固关键线路等其他规划措施提升灾害应对能力。此外,在规划预算和攻击预算的不同取值下,最优配置结果会有所变化,文献[19]通过交叉对比不同攻击预算下得到的最优配置方案在其他攻击场景实现时的表现差异来选择综合最优方案。对于给定的电网系统,可以根据该区域可能面临灾害的严重等级和负荷重要程度选择适合的攻击/规划预算组合,从而识别配置分布式可再生能源电源的关键节点。
在计算效率方面,表2列出了3种不同预算场景的计算时间,模型应用Cplex 12.8.0求解,计算环境为Intel Core i7-6700 3.40 GHz CPU和8 GB RAM的计算机。由于优化模型中二进制变量的存在以及算法在迭代过程中增加约束的特性,应用NCCG算法求解通常需要数十分至数小时。此外,模型求解时间随着规划与攻击预算的增加呈增加趋势。由于分布式电源配置为规划问题,可以进行离线求解,因此求解时间是可以接受的。
表2 3种场景下的求解时间
Table2 Computational time of three scenarios

4.3 可再生能源出力对配置结果的影响
为研究可再生能源出力不确定性的影响,设置两个对照案例,案例1和案例2分别针对场景1和场景2两个单一场景进行优化配置。图6展示了两案例分别在各自场景的t=1时段的负荷恢复情况,线路受到的攻击均为对相应配置方式下的最严重攻击。
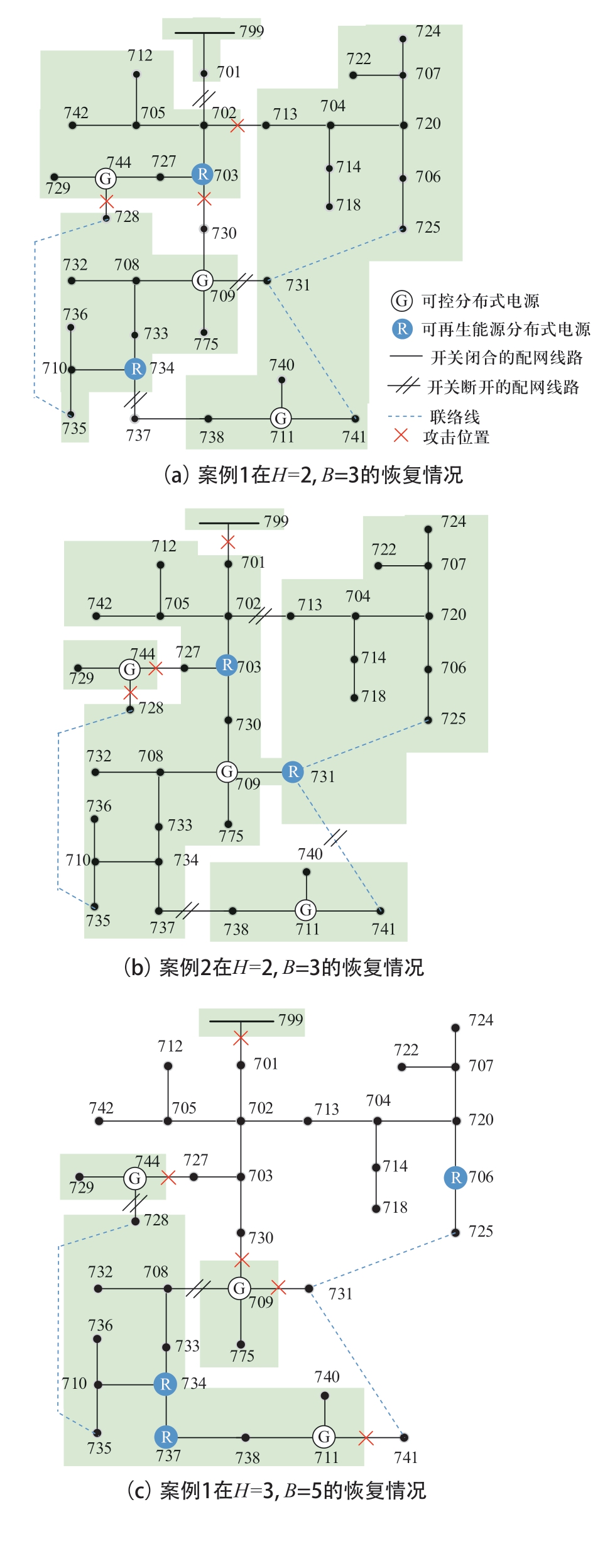
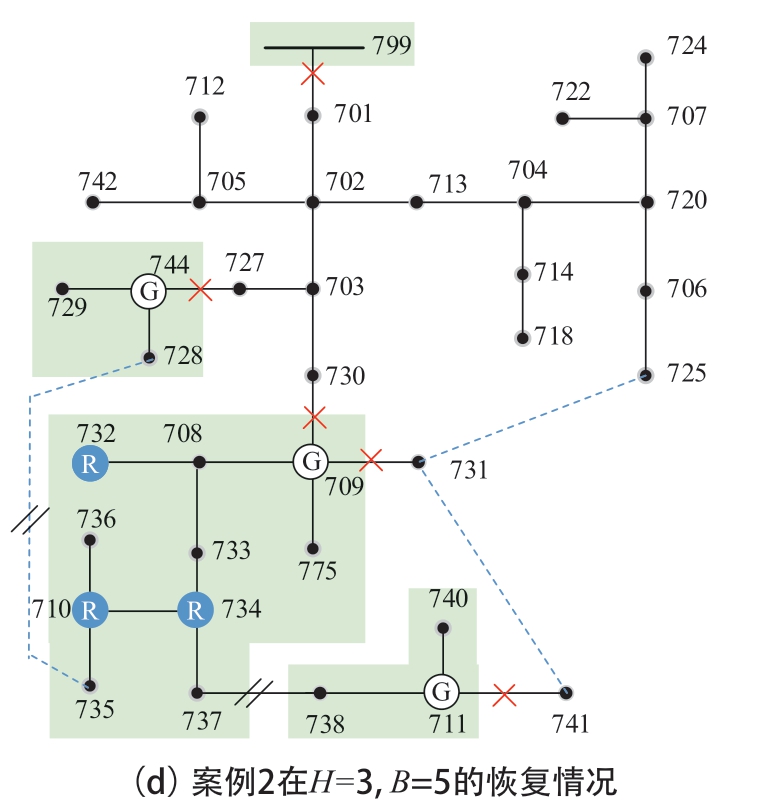
图6 两案例在不同规划与攻击预算下的恢复情况
Fig.6 Restoration process of two cases with different plan/attack budget
对比图6(a)与(b)、(c)与(d)可见,不同可再生能源出力场景下的最优配置结果、对应最严重攻击以及灾后重构方式均有较大差异。仅针对单一出力场景进行最优配置,在对各场景的综合优化效果上会表现不足,因此,需要构建多场景应对可再生能源出力不确定性的影响。
4.4 模型优化效果
为验证模型的鲁棒优化效果,将本文提出的优化配置模型与随机配置进行对比,将分布式可再生能源机组随机配置在节点705、722、775,与机组数量预算H=3下的优化配置结果对比,两种配置方式在相应的最严重攻击下优化时段内各场景切负荷均值如图7所示。
可以看出,采用鲁棒优化模型,能够减小最严重故障下的切负荷损失,对比随机配置的案例具有更好的优化效果。因此,本文所提出的模型能较好地体现系统鲁棒性,提升配电网弹性。
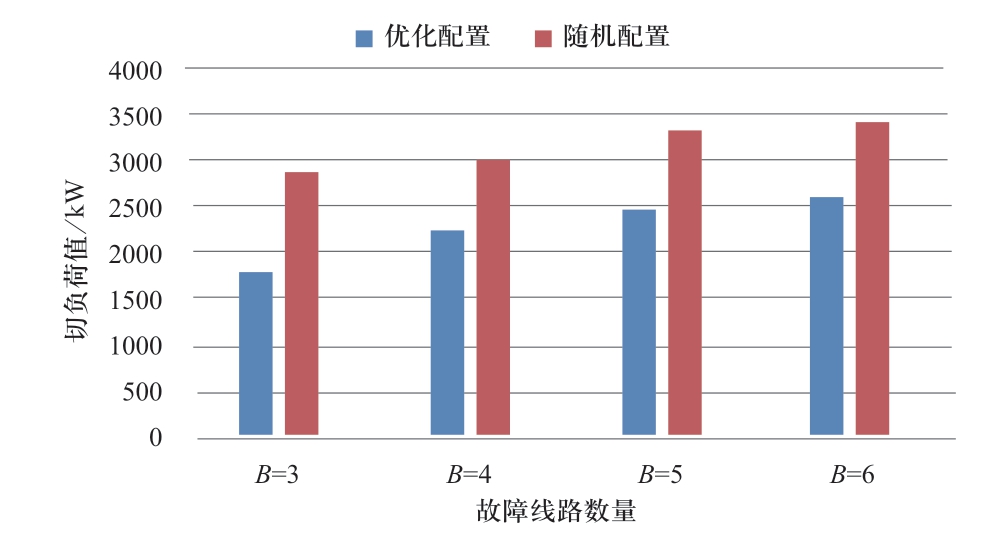
图7 优化配置与随机配置负荷恢复效果比较
Fig.7 Restored load with optimal and random placement
5 结论
本文提出了提升配电网弹性的可再生能源机组最优配置模型,建立故障不确定集的三层鲁棒优化模型,采用NCCG算法求解。针对可再生能源出力不确定性,基于典型出力场景提升综合优化效果。所提模型考虑了灾后配网重构、潮流优化等恢复措施,能够充分发挥分布式电源的负荷支撑作用。在算例中展示了可再生能源出力场景对配置结果的影响,并对模型的有效性进行了验证。
本文提出的分布式可再生能源电源配置模型主要面向配网弹性提升,即保障配网在极端事件下的负荷恢复能力,分布式电源在电网正常运行状态下降低网损、提升运行经济性等方面的作用未在本文研究范畴中。如何兼顾极端灾害下的弹性及正常状态下的经济性,为决策者提供更全面的规划参考,将是后续的重要研究方向。此外,在下一阶段的研究中,需要考虑修复时间不确定性以及动态的元件恢复过程,使模型更加准确。同时,应研究算法的改进及加速方法,提升计算效率,使模型能够适用于大规模算例系统。
参考文献
[1] BIE Z H,LIN Y L,LI G F,et al.Battling the extreme: a study on the power system resilience[J].Proceedings of the IEEE,2017,105(7): 1253-1266.
[2] WANG Y Z,CHEN,WANG J H,et al.Research on resilience of power systems under natural disasters: a review[J].IEEE Transactions on Power Systems,2016,31(2): 1604-1613.
[3] CHEN C,WANG J H,QIU F,et al.Resilient distribution system by microgrids formation after natural disasters[J].IEEE Transactions on Smart Grid,2016,7(2): 958-966.
[4] LEI S B,WANG J H,CHEN,et al.Mobile emergency generator pre-positioning and real-time allocation for resilient response to natural disasters[J].IEEE Transactions on Smart Grid,2018,9(3): 2030-2041.
[5] FARZIN H,FOTUHI-FIRUZABAD M,MOEINI-AGHTAIE M.Enhancing power system resilience through hierarchical outage management in multi-microgrids[J].IEEE Transactions on Smart Grid,2016,7(6): 2869-2879.
[6] 朱正,廖清芬,刘涤尘,等.考虑新能源与电动汽车接入下的主动配电网重构策略[J].电力系统自动化,2015,39(14):82-88,96.
ZHU Zheng,LIAO Qingfen,LIU Dichen,et al.Strategy of distribution network reconfiguration considering wind power and electric vehicle integration[J].Automation of Electric Power Systems,2015,39(14): 82-88,96(in Chinese).
[7] 杨丽君,吕雪姣,李丹,等.含分布式电源的配电网多故障抢修与恢复协调优化策略[J].电力系统自动化,2016,40(20):13-19.
YANG Lijun,LYU Xuejiao,LI Dan,et al.Coordinated optimization strategy of multi-fault repair and recovery for distribution network with distributed generators[J].Automation of Electric Power Systems,2016,40(20): 13-19(in Chinese).
[8] LEI H T,HUANG S J,LIU Y J,et al.Robust optimization for microgrid defense resource planning and allocation against multi-period attacks[J].IEEE Transactions on Smart Grid,2019,10(5): 5841-5850.
[9] YUAN W,WANG J H,QIU F,et al.Robust optimizationbased resilient distribution network planning against natural disasters[J].IEEE Transactions on Smart Grid,2016,7(6): 2817-2826.
[10] GAO H X,CHEN Y,MEI S W,et al.Resilience-oriented pre-hurricane resource allocation in distribution systems considering electric buses[J].Proceedings of the IEEE,2017,105(7): 1214-1233.
[11] DING T,LIN Y L,BIE Z H,et al.A resilient microgrid formation strategy for load restoration considering master-slave distributed generators and topology reconfiguration[J].Applied Energy,2017,199: 205-216.
[12] 刘思聪,周步祥,宋洁,等.考虑分布式电源出力随机性的多目标故障恢复[J].电测与仪表,2018,55(2):123-128.
LIU Sicong,ZHOU Buxiang,SONG Jie,et al.Multiobjective fault restoration considering the randomness of the output of distributed generator[J].Electrical Measurement & Instrumentation,2018,55(2): 123-128(in Chinese).
[13] MCKAY M D,BECKMAN R J,CONOVER W J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J].Technometrics,1979,21(2): 239.
[14] HEITSCH H,RÖMISCH W.Scenario reduction algorithms in stochastic programming[J].Computational Optimization and Applications,2003,24(2/3): 187-206.
[15] MA S S,CHEN B K,WANG Z Y.Resilience enhancement strategy for distribution systems under extreme weather events[J].IEEE Transactions on Smart Grid,2018,9(2): 1442-1451.
[16] DING T,LIN Y L,LI G F,et al.A new model for resilient distribution systems by microgrids formation[J].IEEE Transactions on Power Systems,2017,32(5): 4145-4147.
[17] Zhao Long,Zeng Bo.An exact algorithm for two-stage robust optimization with mixed integer recourse problems[J].University of South Florida,2012.
[18] IEEE PES Distribution System Analysis Subcommittee’s Distribution Test Feeder Working Group.Distribution Test Feeders [EB/OL].http://sites.ieee.org/pes-testfeeders.
[19] FANG Y P,SANSAVINI G.Optimizing power system investments and resilience against attacks[J].Reliability Engineering & System Safety,2017,159: 161-173.
Optimal Renewable Energy Distributed Generators Placement for Resilient Distribution System
BIAN Yiheng1,BIE Zhaohong1*,HUANG Gechao1,ZHOU Qinyong2
(1.School of Electrical Engineering,Xi’an Jiaotong University,Xi’an 710049,Shaanxi Province,China;2.China Electric Power Research Institute,Haidian District,Beijing 100085,China)
Abstract: To improve the resilience of a distribution system and incorporate high-permeability renewable energy under energy transition,we propose the optimal placement model of distributed generator for renewable energy.In this model,the generators are placed at the planning stage.When a fault has occurred,the renewable energy generators and the controllable generators form microgrids under a master-slave operation to support loads in the non-fault areas.A robust optimization method is applied to reduce the load curtailment loss of power system under the worst-case fault,which helped cope with the fault uncertainty.In view of the uncertainty of renewable energy output,typical output scenarios are constructed to improve the comprehensive optimization effect.The optimization is formulated as a tri-level defender-attacker-defender(DAD)framework.On the first level,decision-makers work out the placement scheme.On the second level,the attacker finds the attack strategy with maximum damage.On the third level,restoration measures including plow-flow optimization and topology reconfiguration are undertaken.The nested columnand-constraint generation(NCCG)is applied to solve the problem,and the model effect is validated through IEEE 37-node system.
Keywords: power distribution system; renewable energy; distributed generator; robust optimization; network reconfiguration
作者简介:

卞艺衡
卞艺衡(1994),男,博士研究生,主要研究方向为弹性电网规划与优化运行,E-mail:byh0xyz@stu.xjtu.edu.cn。
别朝红(1970),女,博士,教授,主要研究方向为电力系统规划及可靠性评估、新能源接入系统安全性评估、弹性电力系统。通信作者,E-mail:zhbie@mail.xjtu.edu.cn。
黄格超(1996),男,硕士研究生,主要研究方向为综合能源系统恢复力评估及恢复力提升措施,E-mail:hgc096710@stu.xjtu.edu.cn。
周勤勇(1977),男,博士,教授级高级工程师,主要研究方向为电力系统分析与控制,E-mail:zhouqinyong@126.com。
(责任编辑 张鹏)
