0 引言
随着模块化多电平换流器(modular multilevel converter, MMC)作为柔性直流输电采用的主要换流器拓扑越来越多地出现在电力系统中,MMC引起的谐振稳定性问题逐渐显现,成为威胁电力系统安全运行的问题。福建厦门柔直工程在直流侧曾发生25 Hz左右的次同步振荡现象[1]。鲁西背靠背柔性直流工程在特定工况下,曾发生1270 Hz左右的交流侧谐振现象[2]。与MMC相关的谐振问题逐渐成为业界研究的重点。
目前,针对MMC稳定性的研究方法主要是空间状态法和阻抗分析法。两种方法都是以系统的小信号模型为基础。空间状态法首先根据系统的小信号模型形成空间状态方程,根据空间状态矩阵计算系统的特征根[3-8]。文献[3]以MMC平均值模型为基础,在同步旋转坐标系中建立了考虑模块电容电压二次谐波和二次环流的MMC 10阶小信号模型,其中旋转坐标系包括零序、基频和二倍频坐标系,并将10阶模型同省略了二次谐波和环流抑制器的2阶和6阶系统模型进行了对比。文献[4]按照模块化建模的思想,将直流电网划分为交流系统、MMC和直流网络3部分,首先分别建立各子系统的动态方程,在MMC的建模过程中考虑了桥臂环流、子模块电容电压等MMC内部电气动态及锁相环、环流控制器、信号滤波等环节,最后组合得到整个直流电网的非线性状态空间模型,然后进行线性化得到整个系统的小信号模型。文献[5]基于传统VSC的平均值模型,在建模过程中根据交直流功率等效原理考虑了MMC的损耗,但是并没有考虑MMC的内部动态。文献[6]建立了MMC考虑模块电容电压二次和三次谐波的12阶小信号模型,连同控制系统和测量环节的12阶小信号模型,组成了单端MMC系统的24阶小信号模型,并对系统的稳定性进行了分析验证,所建立的小信号模型提供了与外部控制器和交直流系统进行交互的借口,具有很强的通用性。基于文献[6]提出的小信号模型,文献[7]着重分析了环流抑制策略、桥臂电阻和控制参数等对内部谐波稳定性的影响,通过计算参与因子将MMC系统模态分为“外部模态”和“内部谐波模态”,分析表明MMC内部谐波模态通常呈弱阻尼,换流器桥臂环流、桥臂电阻和外部主控制器增益都对内部谐波模态具有较大影响。文献[8]建立了MMC在交流系统三相不对称时的46阶小信号模型,采用特征根分析研究了正序电流控制器和环流抑制控制器参数的可行域和模态阻尼特征,同样利用参与因子法揭示了主导模态的关键参与电气和控制量。
阻抗分析法已经被广泛地用于两电平VSC变换器的稳定性分析[9-13]。阻抗分析法需要将系统分为电源和负载两个子系统,通过比较电源和负载的阻抗特性,即可分析电力电子装置与电网之间的耦合机理。阻抗分析法不需要计算系统的特征值,但本质还是通过判断系统在右半复平面内不存在极点来判断系统稳定性。通过阻抗分析法判断MMC接入电力系统时的谐振稳定性的前提是获得MMC精确的等效阻抗模型。目前,针对MMC等效阻抗的研究方法主要有解析式推导、谐波线性化和谐波注入法[1, 14-21]。文献[1]忽略了MMC内部谐波的影响,采用MMC的简化模型推导了MMC的直流侧等效阻抗,推导过程中没有考虑功率控制站的功率闭环控制。文献[14]针对采用PR控制器的定交流电压控制,推导了海上风场送出侧MMC的交流侧阻抗,但文章没有涉及采用传统内外环控制器结构的MMC换流站,另外,文章在推导MMC阻抗模型时假设稳态工作点处的上下桥臂电容电压之和与之差分别为2Vdc和0,即忽略了稳态工作点处的SM电容电压波动。文献[15-16]和文献[20]都是采用谐波线性化的方法研究了MMC的交流等效阻抗,模型精度较高,谐波线性化的方法思路简单直观,理论上可以但需要进行复杂的谐波计算。文献[15]首先基于MMC建立了MMC的谐波状态空间模型,再利用谐波线性化原理在MMC交流侧注入谐波小扰动电压,理论上谐波状态空间模型可以包含所有谐波动态,推导过程简单,易于拓展,但考虑的谐波次数很高时,计算量变大,文中只考虑到各状态变量的二次谐波。文献[16]直接在交流电流中注入谐波小扰动信号,利用MMC数学模型直接推导交流电压扰动分量,理论上也可以考虑更多次谐波,但依赖更精确的MMC数学模型,同时计算过程会变得非常复杂。文献[20]利用MMC的频域模型来进行谐波线性化,提出了一种基于矩阵形式的点积运算来简化频域中的卷积计算,该方法同样具有很好的拓展性,只要考虑的谐波次数足够大,理论上同样可以包含所有谐波动态。文献[17-18]采用谐波注入法研究MMC的交流侧等效阻抗。文献[17]中MMC的交流阻抗特性呈现波动并随频率的增加呈下降趋势,但是理论上随着频率的增加,交流电感将起主导作用,交流阻抗应随频率的增加而增加,文献[17]与理论分析不符。文献[18]的结果表明得出的模型在大于100 Hz的频段内能很好的反映MMC的交流阻抗,但在小于100 Hz的频段内误差较大。文献[19]考虑了闭环控制和PLL的影响,推导了MMC作为功率控制站和直流电压控制站的等效阻抗,但是忽略了模块电容电压纹波的影响,另外,也没有考虑PLL对二次电气量和调制量的影响。
MMC交流阻抗的建模可以在abc坐标系和dq坐标系下进行。相比abc坐标系,在dq坐标系下对MMC等效阻抗建模的优点在于:①MMC的控制器通常都是基于dq同步坐标系建立的,因而可以方便地分析控制器对阻抗模型的影响;②电力系统中的发电机等主要元件也是基于dq同步坐标系进行控制和建模,因而对MMC在dq坐标系下进行阻抗建模便于以后扩展到对MMC与电力网络稳定性的联合分析。因此,有必要研究dq坐标系下MMC的全频域等效阻抗模型。
1 推导MMC等效阻抗模型的总体思路
MMC的等效阻抗实质上表示交流母线处交流母线电压与MMC交流电流的微增量关系,因此,推导MMC等效阻抗必须以MMC系统的小信号模型为基础。推导MMC等效模型的总体思路是建立MMC在dq坐标系下的小信号模型,分别以交流母线电压和交流电流作为输入量和输出量,消去小信号模型的中间状态变量,得出输入量到输出量的传递函数矩阵。
如果采用由空间状态方程直接推导传递函数的方法,假设MMC系统在dq坐标系中的状态方程为[21]
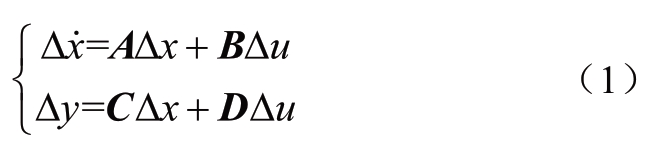
其中:Δx包含了控制器和控制对象所有的状态变量;A为系统状态矩阵。根据文献[21],MMC系统的小信号模型包含18个状态变量,所以A也为18阶。另外,Δu=[Δvtd, Δvtq]为输入量,表示交流电压微增量;Δy=[Δi1d, Δi1q]为输出量,表示交流电流微增量,则交流电压到交流电流的传递函数为
G(s)即MMC系统的等效导纳。但该方法需要对(sI-A)整体求逆,如果需要修改控制器结构,需要重新推导并修改整个A矩阵,不便于建立模块化的阻抗模型库。
因此,本文采用分块求解传递函数的方法,即将MMC系统看作控制器和控制对象(即MMC本体)的组合,分别求解各部分的传递函数,然后消去中间变量。分块求解方法的优势为:①降低了求解时进行求逆计算的阶数,减小了系统计算量;②采用模块化思想,对于不同的控制器实现方式,只需要修改对应的模块,有助于建立系统化的阻抗模型库。
2 全频域阻抗模型
2.1 MMC系统的组成
MMC系统的小信号模型由控制器模型和控制对象模型组成,控制对象模型也即MMC本体的小信号模型。MMC本体和控制器的结构如图1所示。
因为PLL的影响,控制器和控制对象所在dq坐标系的同步角不同,其中,控制器系统又分为基频控制系统和二倍频控制系统,基频控制系统所在dq坐标系的同步角为PLL的输出θpll,而二倍频控制系统所在的dq坐标系同步角为-2θpll。MMC本体所在dq坐标系的同步角为ω0t+α0,ω0为交流系统角频率。两个dq坐标系中变量的变换关系见2.2节。在下文中,MMC本体所在dq坐标系中的变量用上标“s”表示,控制系统所在dq坐标系中的变量用上标“c”表示。

图1 MMC系统的结构
Fig.1 Structure of MMC system
2.2 两个同步dq坐标系之间的变换
基频控制系统和控制对象的dq坐标系之间的关系如图2所示,基频控制系统的dq坐标系同步角为θpll,由PLL给定[13]。系统dq坐标系的同步角为ω0t+α0,在稳态时,θpll0=ω0t+α0。当PLL受到扰动时,两个dq坐标系产生的角度差为Δθpll=θpll -ω0t-α0。

图2 基频控制器和MMC本体所在dq坐标系间的关系
Fig.2 Conversion between dq frames of fundamental frequency controllers and MMC control plant
对于一个固定的矢量f,在两个dq坐标系中的表达式有下列关系:
即
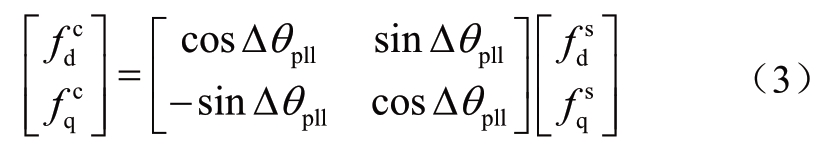
所以

稳态下,![]() 有
有
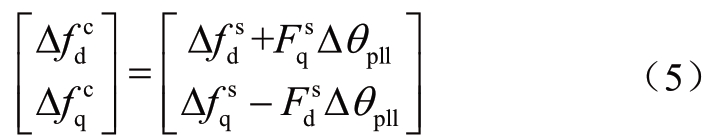
反之
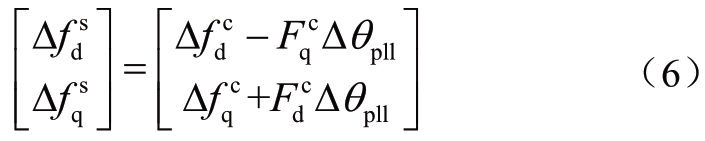
需要注意的是,(5)和(6)为时域中的表达式,因为式(5)和(6)已经进行了线性化,其时域和频域中的表达式相同。在频域中,![]()
控制系统中对二倍频变量进行帕克变换的角度为-2θpll,因此,当PLL受到扰动时,两个dq系统间的角度差为-2Δθpll,类似于式(5),对于二倍频量f2,有
MMC本体与控制系统之间的相关变量需要在两个dq坐标系之间进行变换,从系统坐标系到控制坐标系的变量变换包括:
交流电压:![]()
交流电流:![]()
二倍频环流:![]()
从控制坐标系到系统坐标系的变量变换包括:
基频调制信号:![]()
二倍频调制信号:![]()
①![]()
根据式(5),有
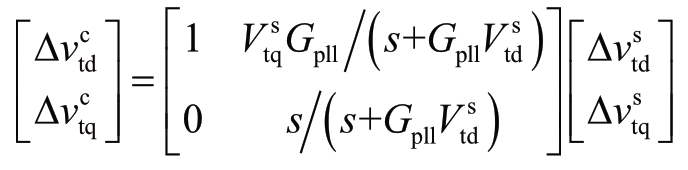
即
②![]()
根据式(5),有
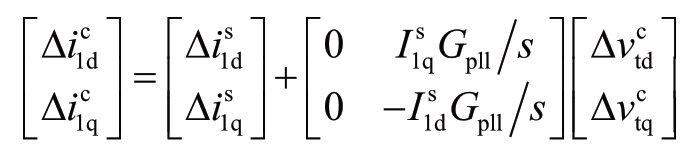
式(8)代入上式,可得
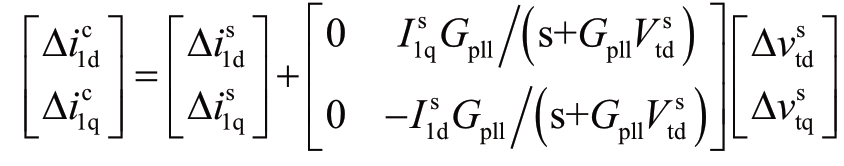
即
③![]()
根据式(7),有
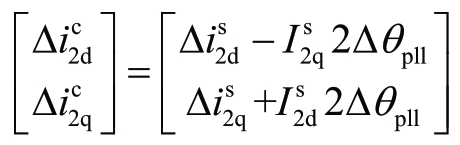
代入式(8),可得
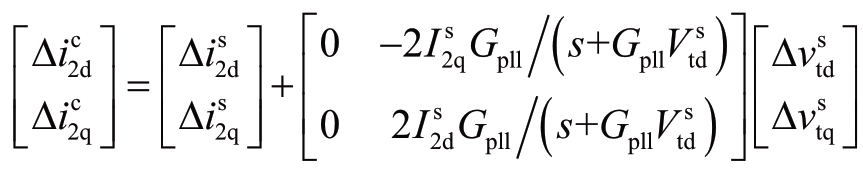
即
④![]()
根据式(6),有
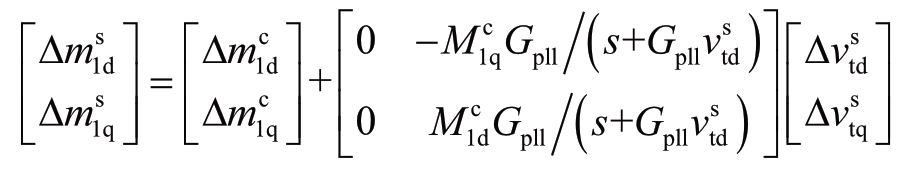
即
⑤![]()
根据式(7),有
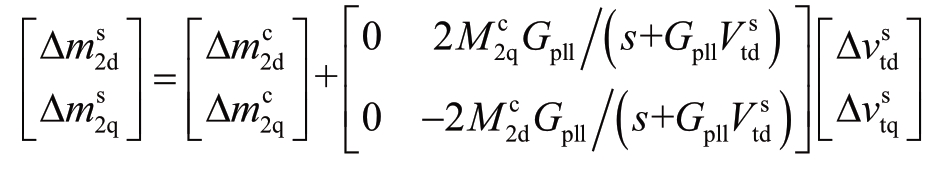
即
2.3 基于平均值的MMC本体小信号模型
MMC的平均值模型的结构如图3所示,以上桥臂为例,上桥臂的串联子模块等效为可控电压源VP;VP由可控电流源ICP与等效电容C组成的外部回路决定。
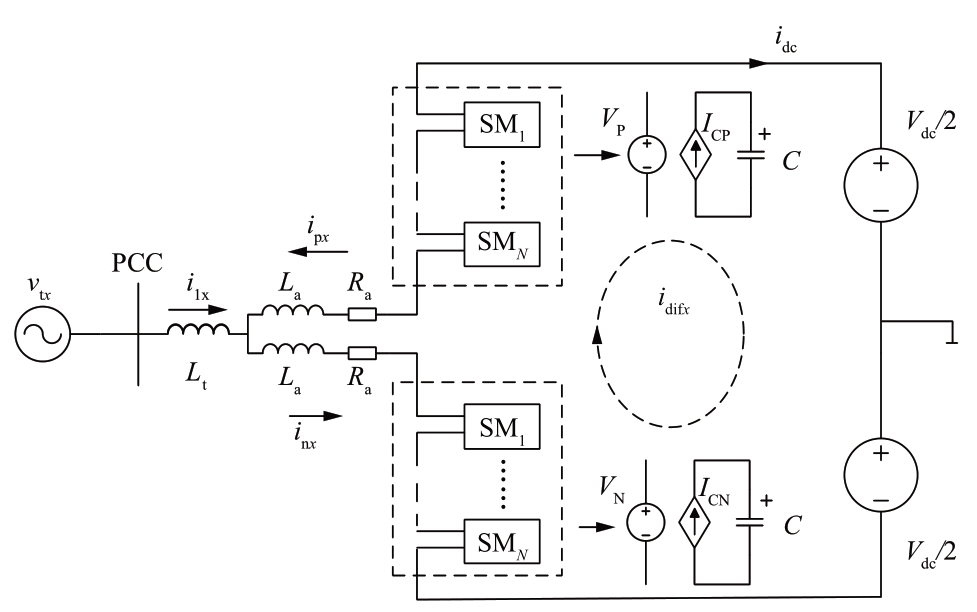
图3 MMC的平均值模型
Fig.3 Averaging model of MMC
MMC换流站可以分为功率控制站和直流电压控制站。功率控制站的外环控制器采用定有功/无功控制,直流电压控制站采用定直流电压/无功控制,各控制器的动态方程如附录B所示。MMC作为功率控制站和直流电压控制站时的小信号模型不同,下文中将分别予以分析。为简便起见,各变量省略了表示电网同步坐标系的上标“s”。
本文只考虑了MMC内部动态的2次谐波,其他低次谐波对交流阻抗有影响有限,已有文献证明大于2次的谐波含量非常小。根据文献[22]中的参数,2次谐波为主要谐波,2次谐波数量至少是4次及更高次谐波的47倍。根据文献[23],高于2次的谐波之和小于 1次谐波的2%,大于2的高次谐波对电气量的推导影响有限。
2.3.1 功率控制站
MMC作为功率控制站时,交流母线电压和直流电压作为输入量,由外部给定,直流电流和交流电流为输出量。在系统dq同步坐标系中,MMC的动态方程如(A1)-(A10)所示,共10个状态变量。对(A1)-(A10)进行线性化,即可得到MMC的小信号模型,本文不再给出详细推导[3]。需要注意的是,本文的小信号模型确实是dq坐标系下基于时域的小信号模型,但是该模型已经经过了线性化,模型中各项均为单独的状态变量Δf或状态变量与一个常数的乘积MΔf,其中M为某一状态变量的稳态值。这样的模型可以直接变换到s域中,并不涉及到s域中的卷积。
下面将MMC功率控制站的小信号模型用传递函数矩阵形式表示,对各输出量、输入量和状态变量进行归类,选择Δi1=[Δi1d, Δi1q]T,Δi2=[Δi2d, Δi2q]T,Δvc=[Δvc0, Δvcd, Δvcq, Δvc2d, Δvc2q]T,Δm1= [Δm1d, Δm1q]T,Δm2=[Δm2d, Δm2q]T和Δvt=[Δvtd, Δvtq]T。其中,Δm1、Δm2、Δvt和Δvdc为输入量,分别代表基频调制比、二次环流调制比、交流电压和直流电压;Δi0、Δi1、Δi2和Δvc为状态量,分别表示桥臂电流直流分量、交流电流、二次环流和等效电容电压。
桥臂电流的直流分量Δi0、交流电流Δi1、二倍频环流Δi2、等效电容电压Δvc可以分别表示为
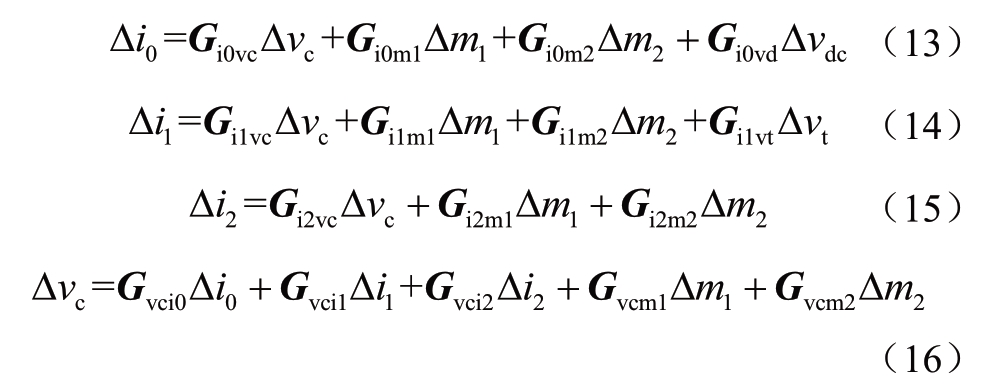
式(13)-(16)中各项的系数矩阵见附录C。
如前所述,交流阻抗实际为交流母线电压Δvt与MMC交流电流Δi1的微增量关系,对于功率控制站,Δvdc为输入,由外部给定,在推导过程中作为扰动量出现。因此,在推导交流阻抗的过程中,Δvdc不会影响交流阻抗的大小,为简便起见,Δvdc=0。
为了推导交流电流Δi1到输入量Δm1、Δm2、Δvt的关系,需要消去状态量Δi0、Δi2和Δvc。
定义Δif=[Δi0, Δi2]T,根据式(13)和(15),
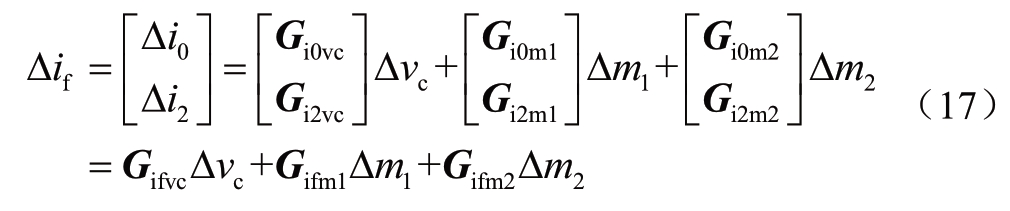
式(16)可以改写为
式中:Gvcif =[Gvci0 Gvci2]。
将式(17)代入(18),可得
式中:G2vci1=GvcGvci1, G2vcm1=Gvc(GvcifGifm1+Gvcm1);G2vcm2=Gvc(GvcifGifm2+Gvcm2), Gvc=(I-GvcifGifvc)-1。
同理,式(19)代入(17),可得
式中:G2ifi1=GifvcG2vci1, G2ifm1=GifvcG2vcm1+Gifm1;G2ifm2 = GifvcG2vcm2+Gifm2。
将式(19)代入(14),可得
式中:G2i1m1=G2i1(Gi1vcG2vcm1 + Gi1m1);G2i1m2 = G2i1(Gi1vcG2vcm2 + Gi1m2);G2i1vt = G2i1Gi1vt;G2i1 =(I-Gi1vc G2vci1)-1。
2.3.2 直流电压控制站
实际的HVDC工程中,MMC作为直流电压控制站时,对端功率控制站一般采用定交流功率控制,直流电流非定值。本文均采用单站仿真计算,为了简化计算,本文假设直流电压控制站直流电压的变化Δvdc不会影响直流电流,即Δidc=0。直流电流由外部给定,直流电压和交流电流为输出量。此时,桥臂电流的直流分量i0等于1/3 idc,不再作为MMC的状态变量。推导MMC作为直流电压控制站的阻抗时,现有模型多是根据交直流功率平衡原理,利用交流功率除以直流电流得出直流电压,从而忽略了MMC内部的谐波动态[1, 5, 24]。本文将从MMC内部状态变量耦合的角度出发推导得出直流电压。
MMC直流电压控制站的动态方程由(A2)-(A10)组成。此时,Δidc(Δi0)为扰动输入量。因此,在推导交流阻抗的过程中,Δidc不会影响交流阻抗的大小,为简便起见,设Δidc=0,即Δi0=0,则(A1)对应的小信号形式为
因此,直流电压Δvdc由MMC本体的内部状态变量Δvc和外部控制信号Δm1和Δm2共同决定,而Δm1和Δm2又是关于Δvdc和状态变量Δi1和Δi2的函数。所以,(22)实际为关于Δvdc的方程,Δvdc由内部状态变量决定,而不能作为独立的输入量。
交流电流Δi1、二倍频环流Δi2和等效电容电压Δvc的表达式保持不变,如式(14)-(16)所示,只是Δi0=0。按照对MMC功率控制站相同的处理方法,需要消去状态量Δi2和Δvc。由于篇幅所限,本文省略了中间推导过程,只给出最终结果:
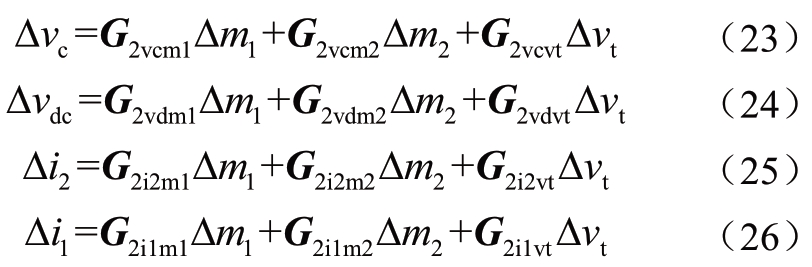
式中:Gvc=(I-Gvci1Gi1vc-Gvci2Gi2vc)-1;G2vcvt=GvcGvci1Gi1vt;G2vcm1=Gvc(Gvci1Gi1m1+Gvci2Gi2m1+Gvcm1);G2vcm2=Gvc(Gvci1Gi1m2+Gvci2Gi2m2+Gvcm2);G2vdm1=GvdvcG2vcm1+Gvdm1,G2vdvt=GvdvcG2vcvt;G2vdm2=GvdvcG2vcm2+Gvdm2,G2i2vt=Gi2vcG2vcvt;G2i2m1=Gi2vcG2vcm1+Gi2m1,G2i2m2=Gi2vcG2vcm2+Gi2m2;G2i1m1=Gi1vcG2vcm1+Gi1m1,G2i1vt=Gi1vcG2vcvt+Gi1vt;G2i1m2=Gi1vcG2vcm2+Gi1m2。
2.4 二倍频环流控制器
二倍频环流控制器的动态方程如(B6)所示。对(B6)进行线性化,考虑到稳态时I2d=I2q=0,ω=ω0,
有
即
根据式(10)和(12),有
2.4.1 功率控制站
对于功率控制站,求解交流阻抗时,如前所述,输入量Δvdc=0,式(28)可以改写为
其中,![]()
将式(20)代入(29),可得
式中:G2m2i1=(I-Gm2i2G2fG2ifm2)-1Gm2i2G2fG2ifi1;G2m2m1=(I-Gm2i2G2fG2ifm2)-1Gm2i2G2fG2ifm1;G2m2vt=(IGm2i2G2fG2ifm2)-1(Tm2+Gm2i2Ti2)。
将式(30)代入(21),可得
式中:G3i1m1=(I-G2i1m2G2m2i1)-1(G2i1m1+G2i1m2G2m2m1);G3i1vt=(I-G2i1m2G2m2i1)-1(G2i1vt+G2i1m2G2m2vt)。
2.4.2 直流电压控制站
对于直流电压控制站,式(24)和(25)代入式(28),解得
式中:Gm2 =(I-Gm2i2G2i2m2-Gm2vdG2vdm2)-1;G2m2m1=Gm2(Gm2i2G2i2m1+Gm2vdG2vdm1);G2m2vt=Gm2(Gm2i2G2i2vt+Gm2vdG2vdvt+ Gm2i2Ti2+Tm2)。
将式(32)代入(26),有
式中:G3i1m1=G2i1m1+G2i1m2G2m2m1;G3i1vt=G2i1vt+
G2i1m2G2m2vt。
2.5 基频控制器
本文中,内环电流控制器和外环控制器统称为基频控制器。内环电流控制器的动态方程如(B5)所示。因为![]() (B5)对应的小信号模型为
(B5)对应的小信号模型为
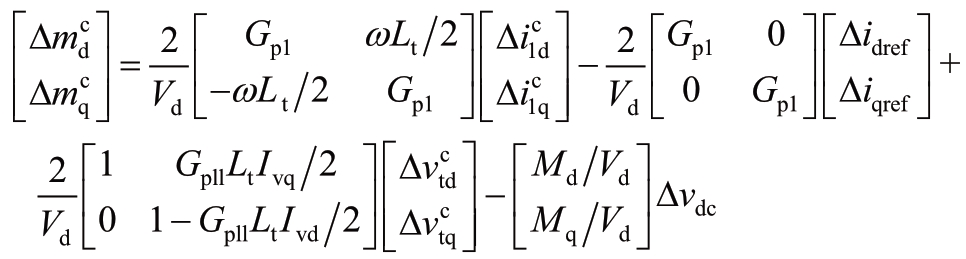
即
2.5.1 功率控制站
对于功率控制站,考虑ΔPref=ΔQref=0,(B3)和(B4)对应的小信号模型为

即
将式(35)代入(34),并考虑输入量Δvdc=0,有
式中:G2m1i1=Gm1i1+Gm1irGiri1;G2m1vt=Gm1vt+Gm1irGirvt。
根据式(8)、(9)和(11),有
式中:G3m1i1=G2m1i1;G2m1vt=Tm1+G2m1i1Ti1+ G2m1vtTvt。
2.5.2 直流电压控制站
对于直流电压控制站,考虑ΔVdref=ΔQref=0,(B2)和(B4)对应的小信号模型为
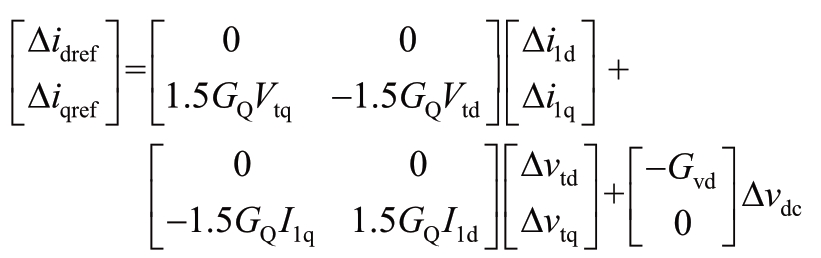
即
将式(38)代入(34),同时根据式(8)、(9)和(11),有
同时,式(32)代入(24),有
式中:G3vdm1=G2vdm1+G2vdm2G2m2m1;G3vdvt=G2vdvt+ G2vdm2G2m2vt。
将式(40)代入(39)中,有
式中:Gm1=(I-G2m1vdG3vdm1)-1;G3m1i1=Gm1G2m1i1;G3m1vt= Gm1(G2m1vt+G2m1vdG3vdvt)。
2.6 交流侧等效阻抗
将式(37)和(41)分别代入式(31)和(33),可以得出功率控制站和直流电压控制站的交流等效阻抗,二者具有相同的表达形式
3 全频域阻抗模型的对比分析
本文采用图1所示的单端MMC系统作为基准测试系统,MMC作为功率控制站和直流电压控制站时,直流侧分别连接直流电压源和直流电流源。基于基准测试系统,对MMC的全频域阻抗模型进行对比分析,系统参数如表1所示。交流阻抗模型所需的稳态工作点通过Matlab的fsolve函数求取。
表1 单端MMC系统参数
Table 1 Simulation parameters of MMC station
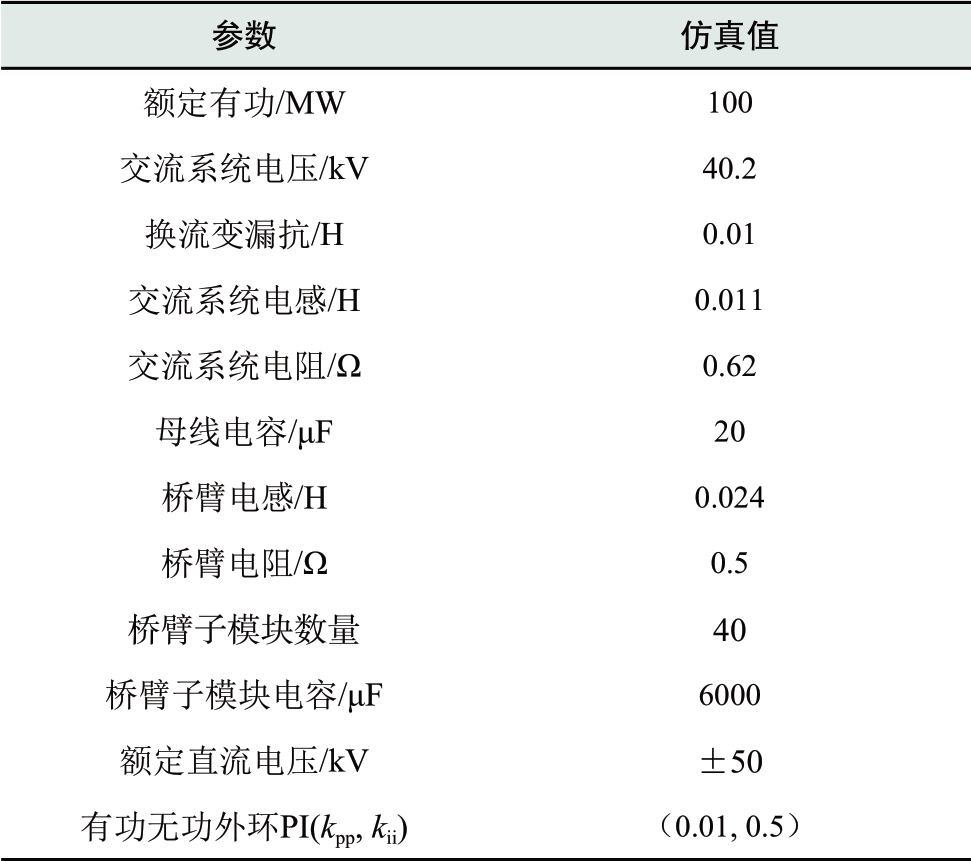
续表

3.1 全频域阻抗模型的准确度
为了校验全频域阻抗模型的准确度,在SIMULINK中建立基准测试系统的仿真模型,测量MMC在系统同步dq坐标系下的交流阻抗,与全频域阻抗模型得出的计算值进行对比。MMC作为功率控制站时,Pref =100 MW,Qref=-50 Mvar,直流电压为100 kV;MMC作为直流电压控制站时,Vdcref=100 kV,Qref = -50 Mvar,Idc=1 kA。交流阻抗的测量值和全频域阻抗模型得出的计算值对比如图4至图7所示。本文中,将10 Hz以下、10~150 Hz、150 Hz以上频段分别称为低频段、中频段和高频段。对于功率控制站,由图4和5可见,在全频域范围内,由全频率阻抗模型得出的计算值与测量值基本一致,只是在100 Hz左右Zdq和Zqd的幅值和相角略有偏差。对于直流电压控制站,图6和7得出的结论相同,全频域阻抗模型得出的计算值与测量值完全吻合,由内部状态变量的耦合关系推导得出直流电压控制站的等效阻抗模型可以准确地反映其交流阻抗特性。根据文献[25]提出的原理,具体的测量方法为:在PCC处串联扰动电压源,测量对应的扰动电流增量,根据(43)计算得出测量阻抗。
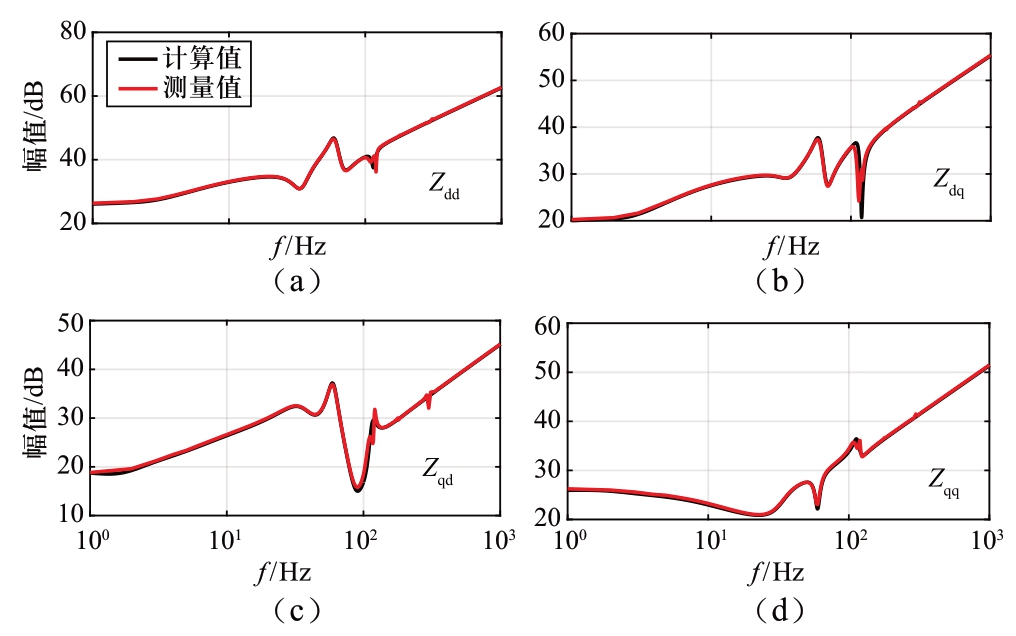
图4 功率控制站交流阻抗幅值的计算值和测量值对比
Fig.4 Comparison between calculation and measurement of AC impedance magnitude of power-controlled stations
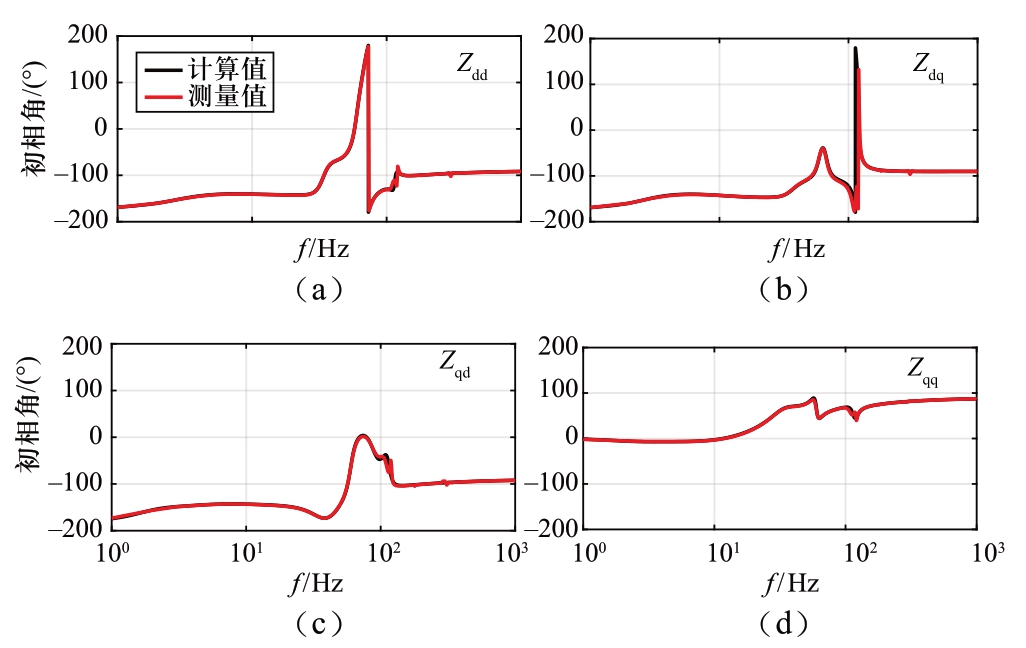
图5 功率控制站交流阻抗相角的计算值和测量值比较
Fig.5 Comparison between calculation and measurement of AC impedance phase angle of power-controlled stations
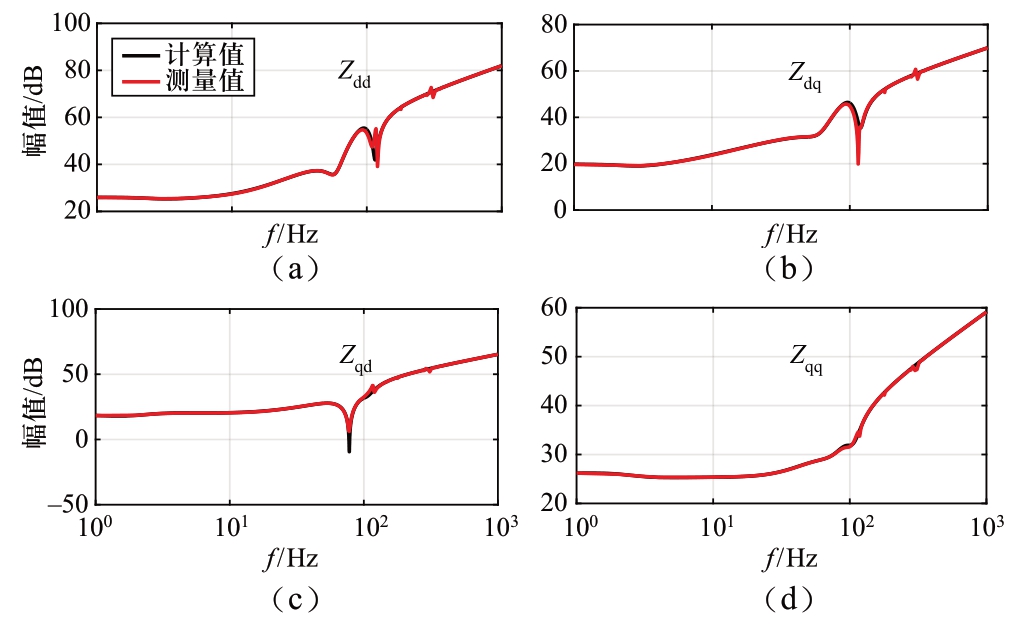
图6 直流电压控制站交流阻抗幅值的计算和测量值对比
Fig.6 Comparison between calculation and measurement of AC impedance magnitude of dc voltage-controlled stations

图7 直流电压控制站交流阻抗相角的计算和测量值对比
Fig.7 Comparison between calculation and measurement of AC impedance phase angle of DC voltage-controlled stations

3.2 与简化模型的对比分析

图8 简化模型与全频域等效模型的等效阻抗幅值的比较
Fig.8 Comparison of ac impedance magnitudes of simplified and full frequency-domain models
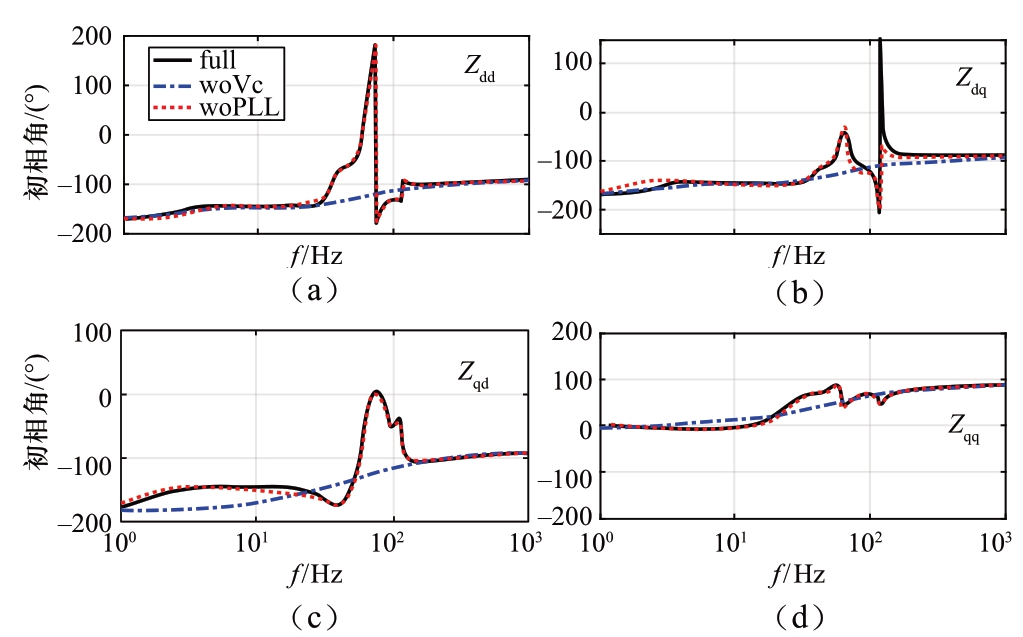
图9 简化模型与全频域等效模型的等效阻抗相角的比较
Fig.9 Comparison of AC impedance phase angles of simplified and full frequency-domain models
为了分析不同环节对MMC等效阻抗的影响,在全频域等效阻抗模型的基础上分别忽略SM电容的动态和PLL的影响,得出的简化模型与全频域等效模型进行对比。对功率控制站和直流电压控制站的简化模型进行对比分析得出的结果近似,为了简单起见,本文只给出了对功率控制站的简化模型和全频频等效模型进行对比分析的结果,如图8和9所示。图中,“full”表示全频域等效阻抗,“woVc”表示忽略了模块电容动态的简化模型,如此MMC实际上等同于两电平VSC,“woPLL”表示忽略了PLL影响的简化模型。
比较全频域等效模型与woVc简化模型,可以发现二者在高频段基本一致,在中频段存在较大差异,表明woVc简化模型不能准确反映MMC交流阻抗在中频段的谐振,也可以得出结论:MMC换流站中频段的谐振由SM电容的动态引起。比较全频域等效模型和woPLL模型,可以发现,虽然woPLL模型在中高频段与全频域模型一致,可以准确反映中频段谐振,但是在低频段会产生一定的偏差。
3.3 稳态工作点对等效阻抗的影响
3.3.1 功率控制站
因为MMC工作在定有功和无功功率模式,
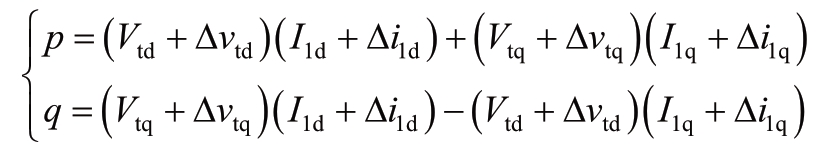
考虑到PLL的作用,Vtq=0,忽略二次无穷小项后,可得
可以解得
其中,
以图4和5为例,其对应的稳态工作点为Vtd= 40.8 kV,P=100 MW,Q=-50 Mvar,即I1d= 1.658 4 kA,I1q=0.829 2 kA。根据(46),有
对应图4中的Zdd=Zqq=25.7 dB,Zdq=Zqd=19.7 dB。
如图5所示,在低频段,Zdd、Zdq和Zqd的相角均为-180°,表现为负电阻特性,Zqq的相角为0°,表现正电阻特性,与理论分析一致。随着频率的增加,在高频段,Zdd、Zdq和Zqd均表现为负电感特性,而Zqq表现为正电感特性。
图10给出了MMC和两电平VSC工作在单位功率因数的阻抗特性曲线。如图所示,VSC的Zdq和Zqd远远小于Zdd和Zqq,因此,对并网型VSC而言,可以将Zdq和Zqd近似为零。然而,虽然MMC的Zdq和Zqd在低频段的幅值很小,但是随着频率的增加,Zdq和Zqd迅速增加到Zdd和Zqq的水平。此外,MMC通常不是工作在单位功率因数,Zdq和Zqd较大,如图4所示。因此,不同于传统VSC,对MMC而言,不能将Zdq和Zqd近似为零。
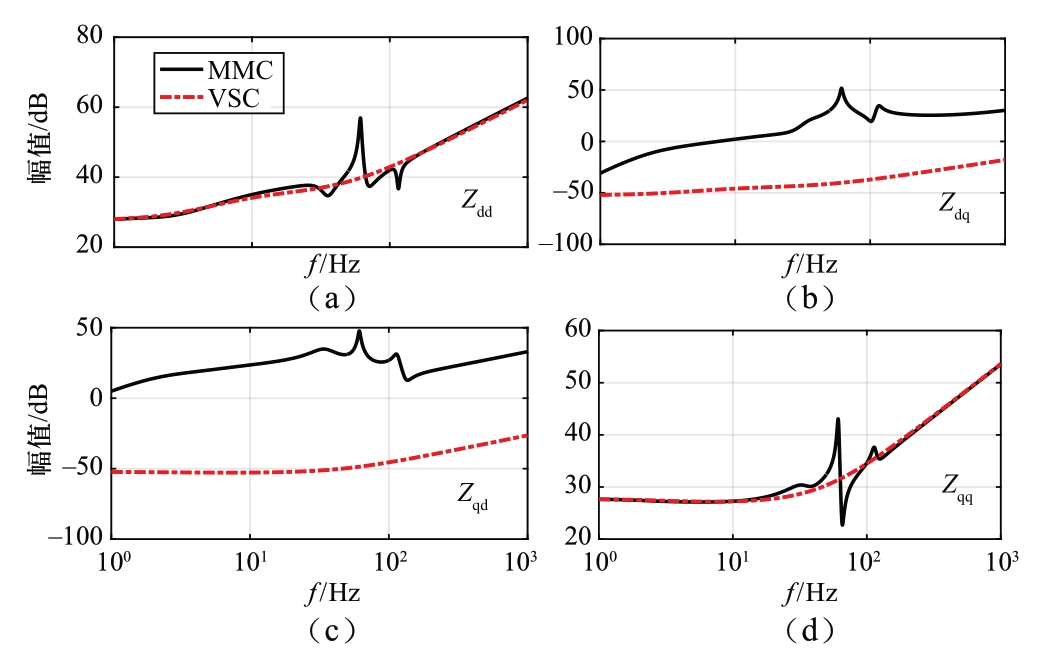
图10 MMC和VSC在单位功率因数时的交流阻抗对比
Fig.10 Comparison of ac impedance magnitude between MMC and VSC with unity power factor
3.3.2 直流电压控制站
对于直流电压控制站,发生扰动后,因为直流电流和直流电压均保持恒定,忽略因扰动产生的损耗变化,交流侧功率保持不变。因此,直流电压控制站的阻抗特性与功率控制站类似,与稳态功率的方向相关。对于直流电压控制站,式(46)仍然成立。图7和图11分别对应Idc=1 kA和Idc=-1 kA,由图可见,低频段,Zdd的相角分别为-180°和0°,表现为负电阻和正电阻特性,与理论分析一致。
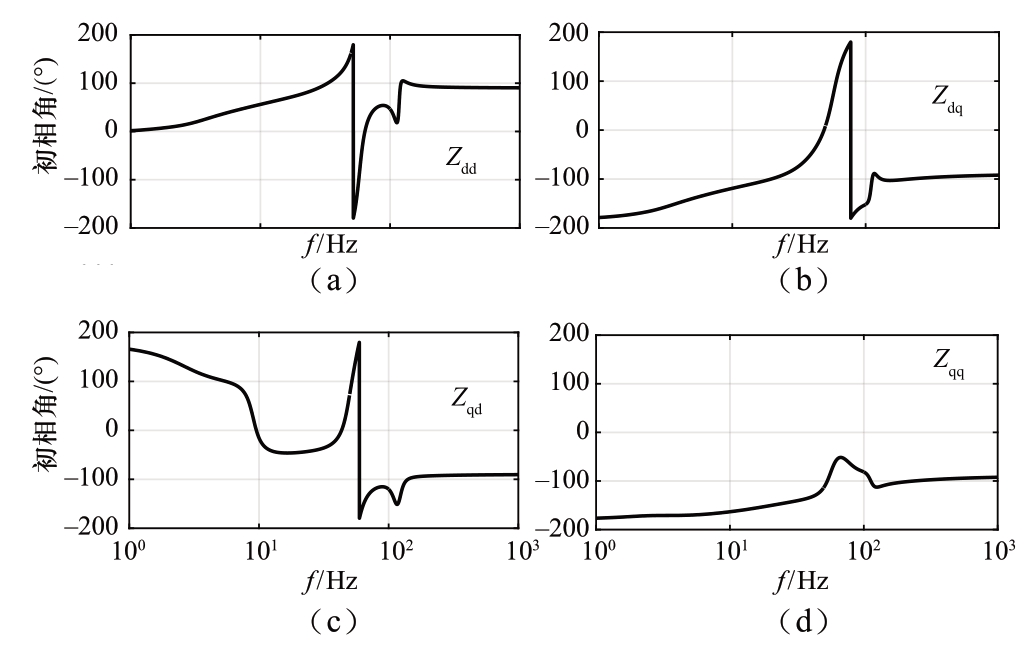
图11 Idc= -1 kA时直流电压控制站的交流阻抗相角
Fig.11 AC impedance phase angle of dc voltage control station when Idc=-1 kA
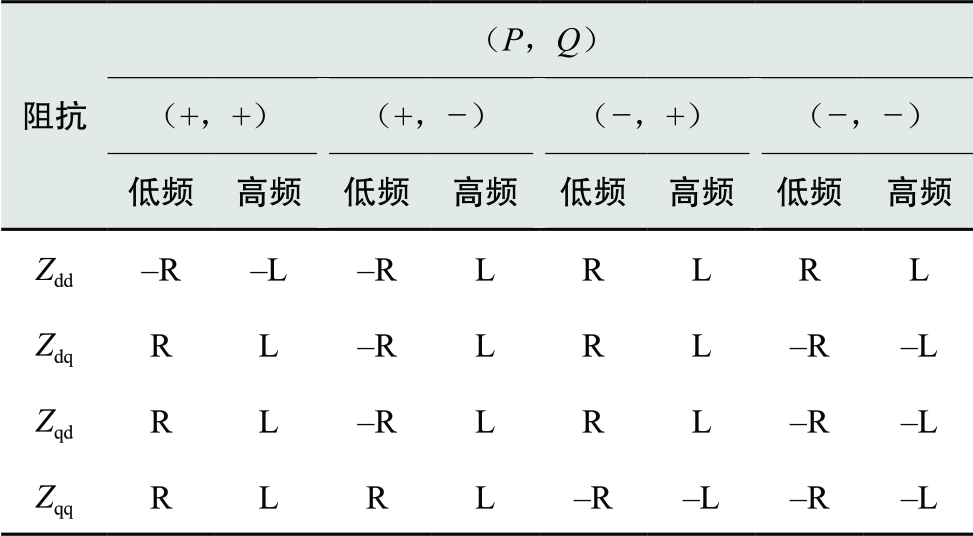
表2和表3分别为功率控制站和直流电压控制站的全频域等效阻抗在不同工况下的特性。对比表2和表3,可以发现,MMC的交流阻抗在低频段表现为电阻,电阻的正负由稳态功率的方向决定。MMC在高频段表现为电感。Zmmc在低频段与稳态电流的关系如式(46)所示。
另外,功率控制站和直流电压控制站在低频段和高频段的特性基本一致,只是直流电压控制站在正有功、负无功工况下,Zdd、Zdq和Zqd表现为负电感,与功率控制站的特性相反,如表3粗体部分所示。
表2 功率控制站在不同工况下的特性
Table 2 Characteristic of power-control stations with various(P, Q)
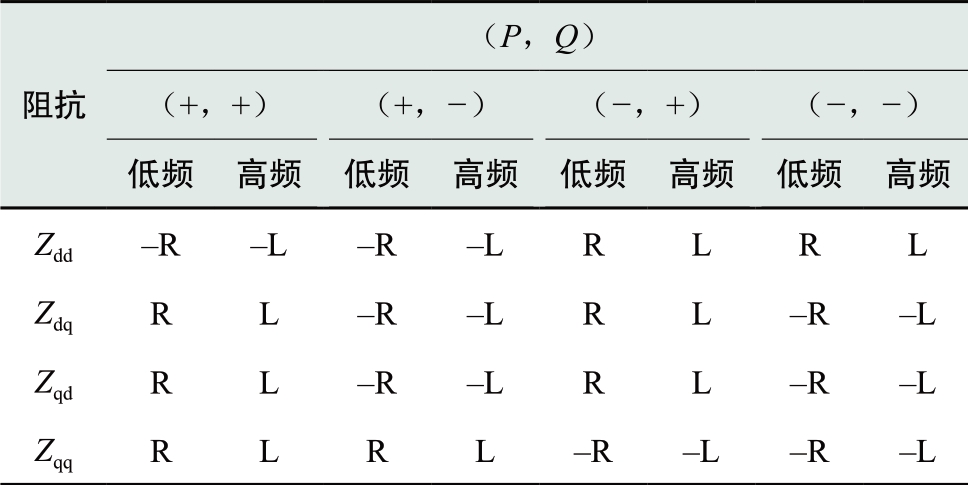
表3 直流电压控制站在不同工况下的特性
Table 3 Characteristic of DC voltage-control stations with various(P, Q)
4 基于全频域阻抗模型的稳定性分析
如图12所示,MMC换流站通过PCC与交流系统相连,其中,Zg为交流系统阻抗,Zc为PCC处的并联电容,Zmmc为MMC在PCC处等效的交流阻抗。MMC作为功率控制站运行。在系统同步坐标系下,有
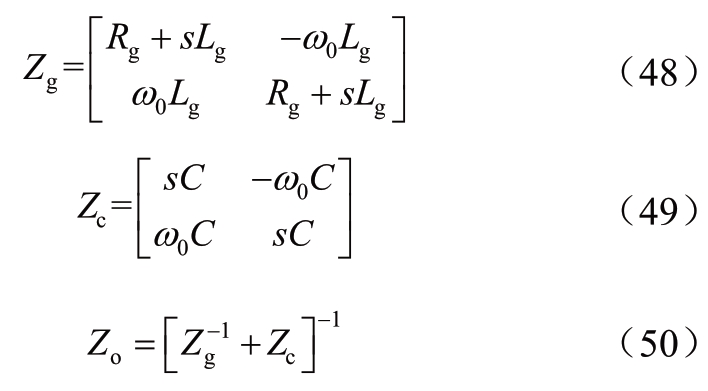
定义回路比矩阵为
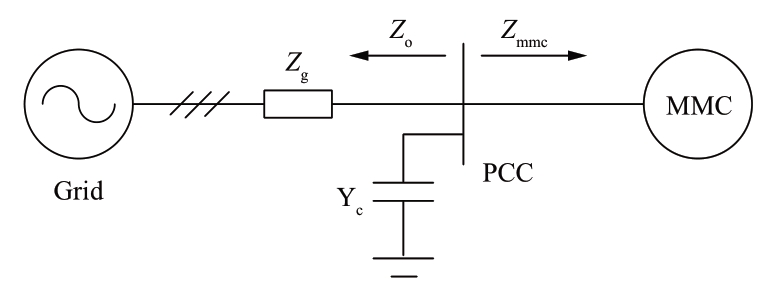
图12 MMC连接交流系统的示意图
Fig.12 MMC interfaced with AC grid
根据广义奈奎斯特判据,对于多输入多输出系统,如果ℓ的特征值轨迹逆时针包围(-1, j0)点的圈数等于ℓ在右半平面的极点个数,则系统闭环稳定。
如果闭环增益表示为Tcl=(1+ℓ)-1,则广义奈奎斯特稳定判据可以表示为
其中,P(x)表示x在右半平面的极点个数,N(-1, j0)(x)表示x的特征值轨迹围绕(-1, j0)点的圈数。对于实际的物理系统,回路比ℓ在右半平面的极点个数通常为0[26]。
4.1 连接不同的交流系统时的稳定性判断
交流系统的参数如表1所示,其中,Ls=0.011 H。此时,ℓ的特征值轨迹如图13所示。如图所见,特征值λ1和λ2的轨迹都没有包围(-1, j0)点,所以ACMMC系统是稳定的。
图14为Ls=0.033 H时ℓ的特征值轨迹。由图14(b)可见,λ1的轨迹没有包围(-1, j0)点,而λ2的轨迹穿过(-1, j0)点附近并包围(-1, j0)点两圈,λ2的轨迹穿越实轴的频率为218.4 Hz。因此,AC-MMC系统是不稳定的,但接近临界稳定。图15所示为改变Ls时交流电流d轴分量i1d的时域仿真曲线,其中,Ls在1 s时由0.011 H增大为0.033 H。可以发现,i1d在1 s后出现谐振现象,谐振周期为4.60 ms,对应的谐振频率为217.4 Hz,与特征值轨迹的预测结果218.4 Hz一致,谐波有放大的趋势,接近临界稳定。
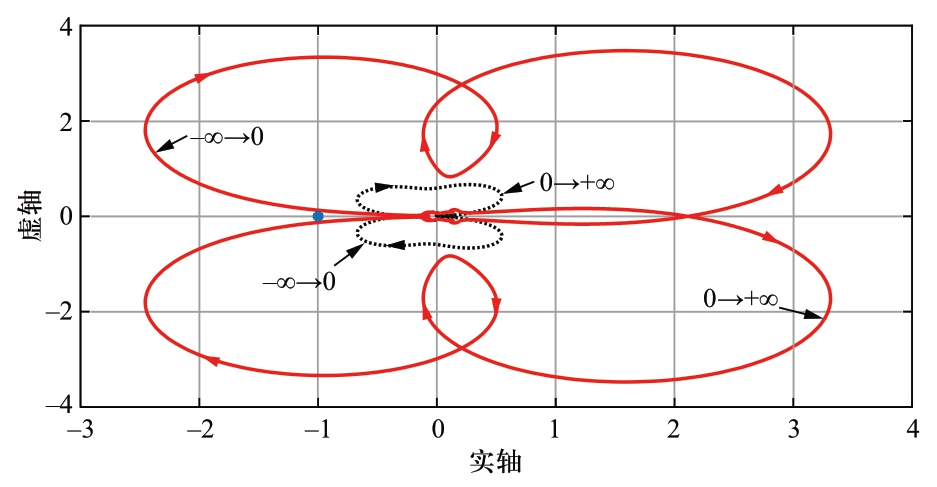
图13 Ls=0.011 H时ℓ的特征值轨迹
Fig.13 Eigenvalue loci of ℓ when Ls=0.011 H
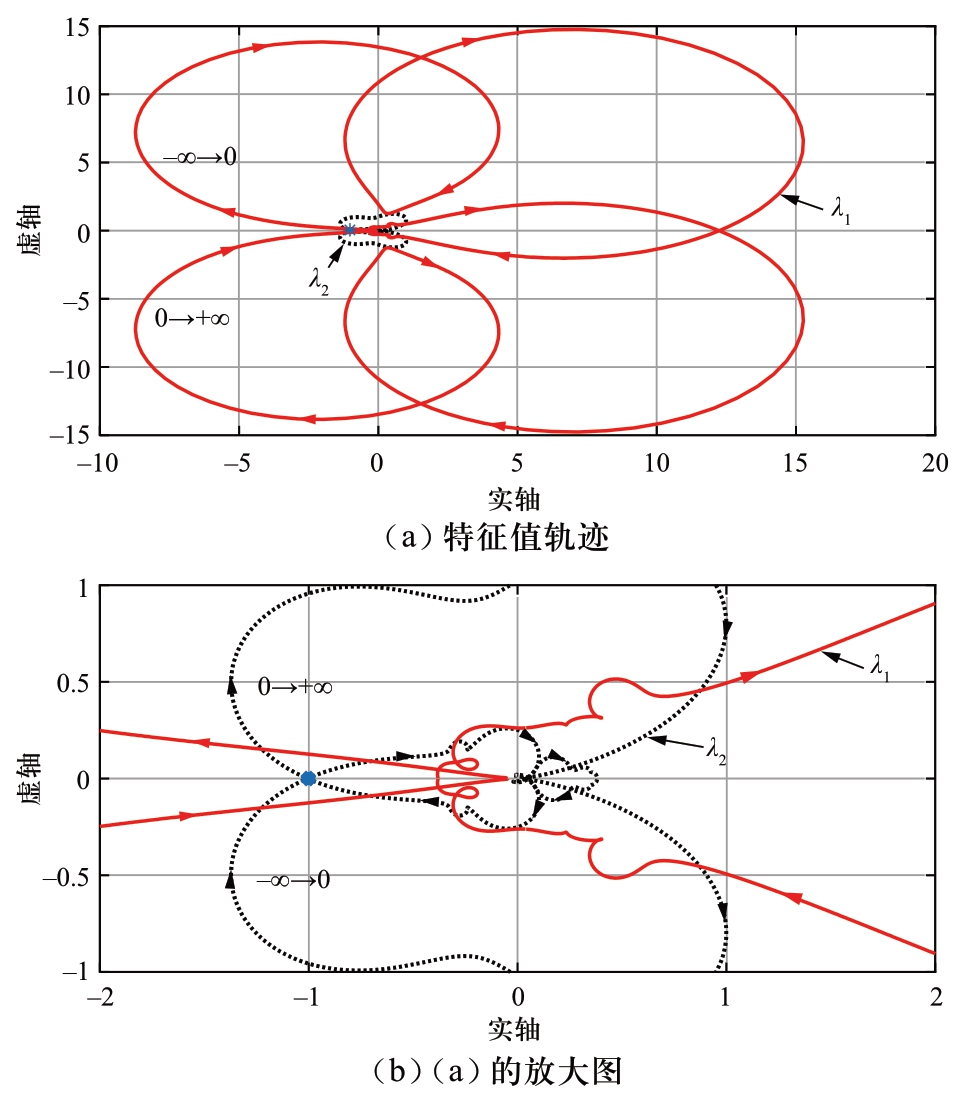
图14 Ls=0.033 H时ℓ的特征值轨迹
Fig.14 Eigenvalue loci of ℓ when Ls=0.033 H
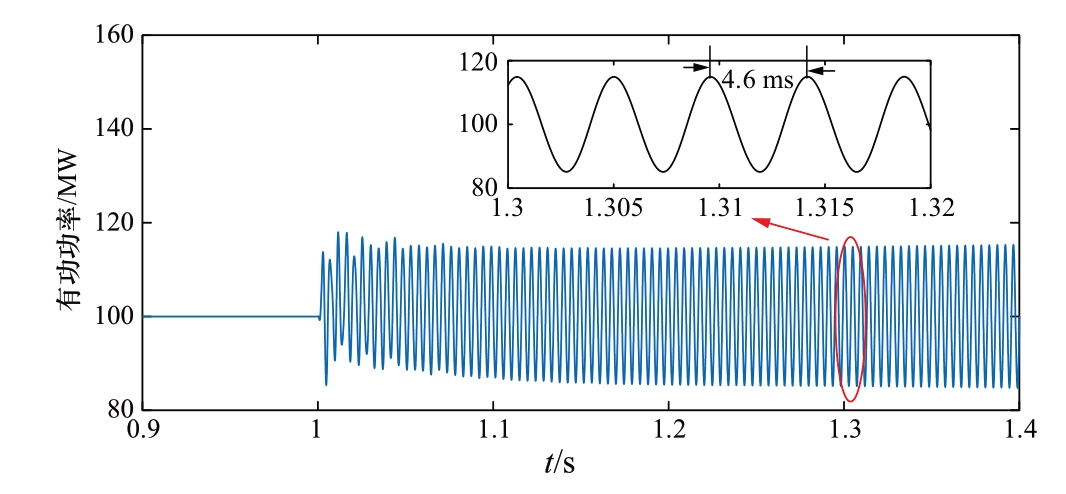
图15 Ls由0.011变为0.033 H时交流电流d轴分量曲线
Fig.15 D-axis component of AC current when Ls changes from 0.011 to 0.033 H.
4.2 控制参数变化时的稳定性判断
本节中,在PSCAD中建立MMC功率控制站的详细模型,对控制系统的相关参数进行变化时的稳定性进行分析判断。交流系统保持不变,交流系统电压Usm=32.1 kV,Ls=0.011 H。当有功和无功外环控制器的比例系数kpp和kqp发生变化时,有功功率的暂态波形如图16所示。其中,1.0 s之前,kpp= kqp=0.03,在1.0 s至1.4 s时,kpp=kqp=0.034,在1.4 s之后,kpp=kqp=0.038。由图16可知,在1 s至1.4 s,有功功率波形的纹波相比1 s中之前变大,而在1.4 s之后,有功功率发生谐振失稳。图17为对应不同控制参数的ℓ的特征值轨迹,因为与图14的特征值轨迹类似,λ1的轨迹均不包围(-1, j0)点,所以为了便于显示,图17只给出了特征值λ2的轨迹。其中,图17(a)对应kpp=kqp=0.034,此时,λ2的轨迹恰好穿越(-1, j0)点,对应图16中1.0 ~1.4 s时有功功率的临界稳定状态;图17(b)对应kpp=kqp=0.038,λ2的轨迹包围(-1, j0)点,系统不稳定,此时λ2的轨迹穿越实轴的频率为约为275 Hz,而图16中1.4 s后有功功率失稳时的谐振周期为3.80 ms,对应的谐振频率为263 Hz,与特征值轨迹预测的谐振频率275 Hz基本一致。所以,在其他参数确定的情况下,保证系统稳定的功率外环控制器比例系数取值应小于0.034。图18为dq坐标系下不同带宽时的阻抗特性曲线。

图16 PSCAD仿真得出的功率外环控制器比例系数变化时的有功功率曲线
Fig.16 Active power from PSCAD when proportional factor of outer control loop changes
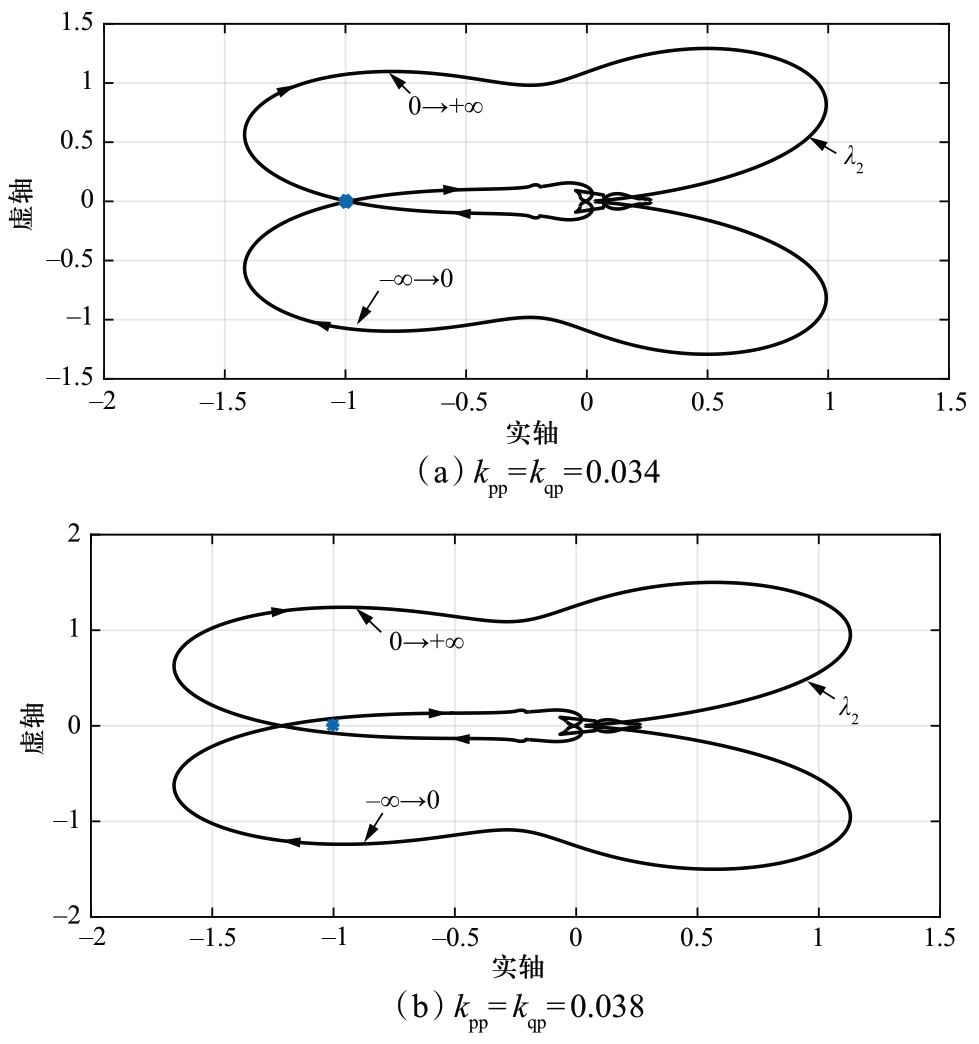
图17 图16对应的ℓ的特征值轨迹
Fig.17 Eigenvalue loci of ℓ corresponding to Fig.16

图18 kpp=0.03、0.034和0.038时对应的阻抗特性曲线
Fig.18 AC impedance magnitudes of kpp=0.03, 0.034 and 0.038
5 结论
1)全频域阻抗模型考虑了PLL对控制信号和反馈信号的影响以及内外环控制器的闭环控制,理论上具有和小信号模型的系统状态矩阵相同的阶数,因而能够更准确地反映MMC在整个频域上的阻抗特性。MMC作为直流电压控制站运行时,直流电压作为输出,应由内部状态变量的耦合关系决定。仿真结果证明了推导得出的等效阻抗模型的正确性。
2)MMC的交流阻抗在中频段(10~150 Hz)存在谐振,模块电容动态是产生中频段谐振的原因;忽略PLL的动态会影响MMC交流阻抗模型在中低频段的准确性;与传统两电平VSC不同,MMC工作在单位功率因数工况下,d轴和q轴的耦合阻抗不能忽略。
3)MMC交流阻抗矩阵的各元素在低频段表现为电阻特性,电阻的正负由稳态功率的方向决定,而在高频段表现为电感特性。这与常规物理上的理解一致:低频时MMC的交流感抗远远小于电阻,电阻起主导作用,而在高频时MMC的交流感抗远远大于电阻,电感起主导作用。
4)采用广义奈奎斯特判据,全频域阻抗模型可以准确地对系统的稳定性进行判断。
参考文献
[1]李云丰,汤广福,贺之渊,等.MMC型直流输电系统阻尼控制策略研究[J].中国电机工程学报,2016,36(20):5492-5503.
LI Yunfeng, TANG Guangfu, HE Zhiyuan, et al.Damping control strategy research for MMC based HVDC system[J].Proceedings of the CSEE, 2016, 36(20):5492-5503(in Chinese).
[2]许树楷.南方电网大功率电力电子研究应用于运行经验[C]//中国电机工程学会直流输电与电力电子专业委员会年会,武汉,2017.
[3]JAMSHIDI FAR A, JOVCIC D.Small-signal dynamic DQ model of modular multilevel converter for system studies[J].IEEE Transactions on Power Delivery, 2016, 31(1):191-199.
[4]鲁晓军,林卫星,向往,等.基于模块化多电平换流器的直流电网小信号建模[J].中国电机工程学报,2018,38(4):1143-1156.
LU Xiaojun, LIN Weixing, XIANG Wang, et al.Small signal modeling of MMC-based DC grid[J].Proceedings of the CSEE, 2018, 38(4):1143-1156(in Chinese).
[5]喻悦箫,刘天琪,王顺亮,等.基于平均值模型的双端MMC-HVDC系统小信号建模[J].中国电机工程学报,2018, 38(10):2999-3006.
YU Yuexiao, LIU Tianqi, WANG Shunliang, et al.Small signal modeling of two-terminal MMC-HVDC based on AVM model[J].Proceedings of the CSEE, 2018, 38(10):2999-3006(in Chinese).
[6]李探,Aniruddha M.Gole,赵成勇.考虑内部动态特性的模块化多电平换流器小信号模型[J].中国电机工程学报,2016,36(11):2890-2899.
LI Tan, GOLE M A, ZHAO Chengyong.Small-signal model of the modular multilevel converter considering the internal dynamics[J].Proceedings of the CSEE, 2016, 36(11):2890-2899(in Chinese).
[7]李探,赵成勇,Aniruddha M.Gole.MMC-HVDC内部谐波模态识别及其稳定性分析[J].中国电机工程学报,2017,37(8):2185-2195.
LI Tan, ZHAO Chengyong, GOLE M A.Identification and stability analysis of the internal harmonic modes of the MMCHVDC system[J].Proceedings of the CSEE, 2017, 37(8):2185-2195(in Chinese).
[8]杨佳艺,赵成勇,郭春义.交流系统不对称时MMC系统小信号稳定性研究[J].中国电机工程学报,2018,38(12):3651-3661.
YANG Jiayi, ZHAO Chengyong, GUO Chunyi.Smallsignal stability analysis of modular multilevel converter under unbalanced grid conditions[J].Proceedings of the CSEE, 2018, 38(12):3651-3661(in Chinese).
[9]XU L, FAN L L.Impedance-based resonance analysis in a VSC-HVDC system[J].IEEE Transactions on Power Delivery, 2013, 28(4):2209-2216.
[10]CAO W C, MA Y W, YANG L, et al.D-Q impedance based stability analysis and parameter design of three-phase inverterbased AC power systems[J].IEEE Transactions on Industrial Electronics, 2017, 64(7):6017-6028.
[11]WEN B, BOROYEVICH D, BURGOS R, et al.Analysis of D-Q small-signal impedance of grid-tied inverters[J].IEEE Transactions on Power Electronics, 2016, 31(1):675-687.
[12]佟强,张东来,徐殿国.分布式电源系统中变换器的输出阻抗与稳定性分析[J].中国电机工程学报,2011, 31(12):57-64.
TONG Qiang, ZHANG Donglai, XU Dianguo.Output impedance and stability analysis of converters in distributed power systems[J].Proceedings of the CSEE, 2011, 31(12):57-64(in Chinese).
[13]辛焕海,李子恒,董炜,等.三相变流器并网系统的广义阻抗及稳定判据[J].中国电机工程学报,2017,37(5):1277-1292.
XIN Huanhai, LI Ziheng, DONG Wei, et al.Generalizedimpedance and stability criterion for grid-connected converters [J].Proceedings of the CSEE, 2017, 37(5):1277-1292(in Chinese).
[14]吕敬,蔡旭,张占奎,等.海上风电场经MMC-HVDC并网的阻抗建模及稳定性分析[J].中国电机工程学报,2016,36(14):3771-3781.
LÜ Jing, CAI Xu, ZHANG Zhankui, et al.Impedance modeling and stability analysis of MMC-based HVDC for offshore wind farms[J].Proceedings of the CSEE, 2016, 36(14):3771-3781(in Chinese).
[15]吕敬,蔡旭.提高风场柔直并网系统稳定性的控制器参数优化设计[J].中国电机工程学报,2018,38(2):431-443.
LÜ Jing, CAI Xu.Controller parameters optimization design for enhancing the stability of wind farm with VSC-HVDC system[J].Proceedings of the CSEE, 2018, 38(2):431-443(in Chinese).
[16]吕敬,蔡旭.基于谐波线性化的模块化多电平换流器阻抗建模[J].电力系统自动化,2017,41(4):136-142.
LYU Jing, CAI Xu.Harmonic linearization based impedance modeling of modular multilevel converters[J].Automation of Electric Power Systems, 2017, 41(4):136-142(in Chinese).
[17]薛英林,徐政,张哲任,等.MMC-HVDC换流器阻抗频率特性分析[J].中国电机工程学报,2014,34(24):4040-4048.
XUE Yinglin, XU Zheng, ZHANG Zheren, et al.Analysis on converter impedance-frequency characteristics of the MMCHVDC system[J].Proceedings of the CSEE, 2014, 34(24):4040-4048(in Chinese).
[18]徐政.柔性直流输电系统[M].北京:机械工业出版社,2013:50-57.
[19]KHAZAEI J, BEZA M, BONGIORNO M.Impedance analysis of modular multi-level converters connected to weak AC grids[J].IEEE Transactions on Power Systems, 2018, 33(4):4015-4025.
[20]SUN J, LIU H C.Sequence impedance modeling of modular multilevel converters[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4):1427-1443.
[21]李正,郝全睿,尹晓东,等.模块化多电平换流器的降阶小信号模型研究[J].中国电机工程学报,2018,38(12):3638-3650.
LI Zheng, HAO Quanrui, YIN Xiaodong, et al.Research on reduced-order small-signal model of modular multilevel converter[J].Proceedings of the CSEE, 2018, 38(12):3638-3650(in Chinese).
[22]ILVES K, ANTONOPOULOS A, NORRGA S, et al.Steadystate analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters[J].IEEE Transactions on Power Electronics, 2012, 27(1):57-68.
[23]SKOGESTAD S, POSTLETHWAITE I.Multivariable feedback control:analysis and design [M].John Wiley& Sons, 2005:148-160.
[24]SAAD H, FILLION Y, DESCHANVRES S, et al.On resonances and harmonics in HVDC-MMC station connected to AC grid[J].IEEE Transactions on Power Delivery, 2017, 32(3):1565-1573.
[25]FRANCIS G, BURGOS R, BOROYEVICH D, et al.An algorithm and implementation system for measuring impedance in the D-Q domain[C]//2011 IEEE Energy Conversion Congress and Exposition, September 17-22, 2011.Phoenix, AZ, USA:IEEE, 2011.
[26]XIAO H Q, XU Z, TANG G, et al.Complete mathematical model derivation for modular multilevel converter based on successive approximation approach[J].IET Power Electronics, 2015, 8(12):2396-2410.
附 录
A 同步旋转dq坐标系下MMC微分方程
MMC内部环流直流分量,二倍频dq分量的动态方程为:
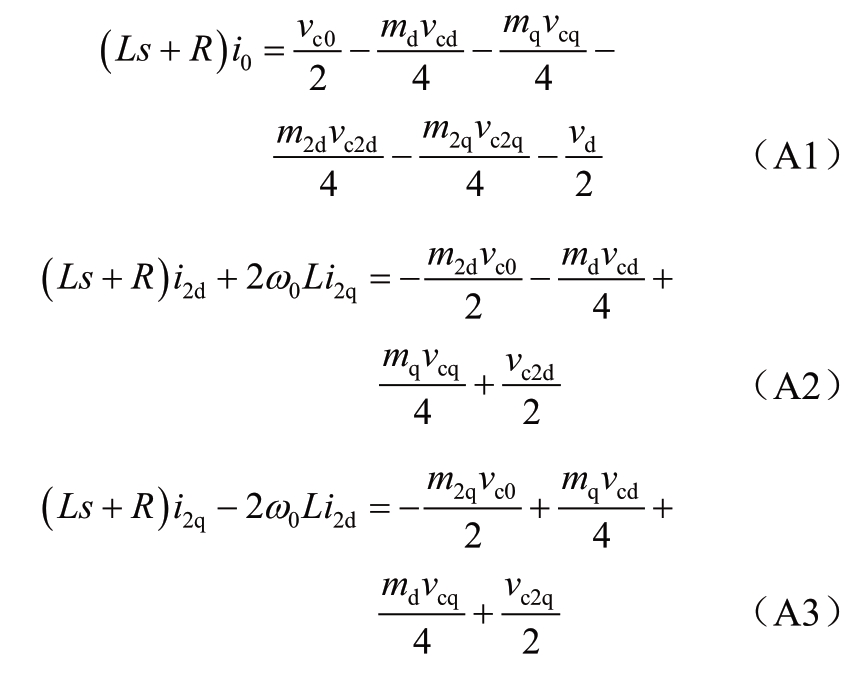
MMC交流侧电流基频dq分量的动态方程为:
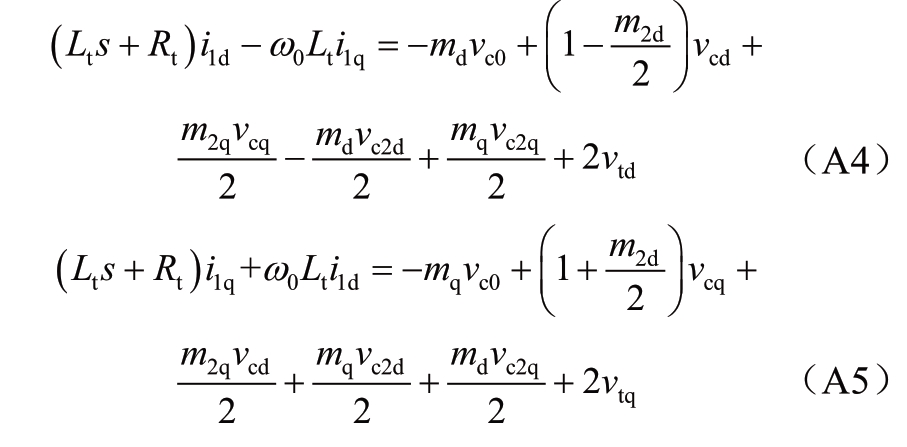
MMC上桥臂串联子模块等效电容电压直流分量、基频dq分量、二倍频dq分量的动态方程为:
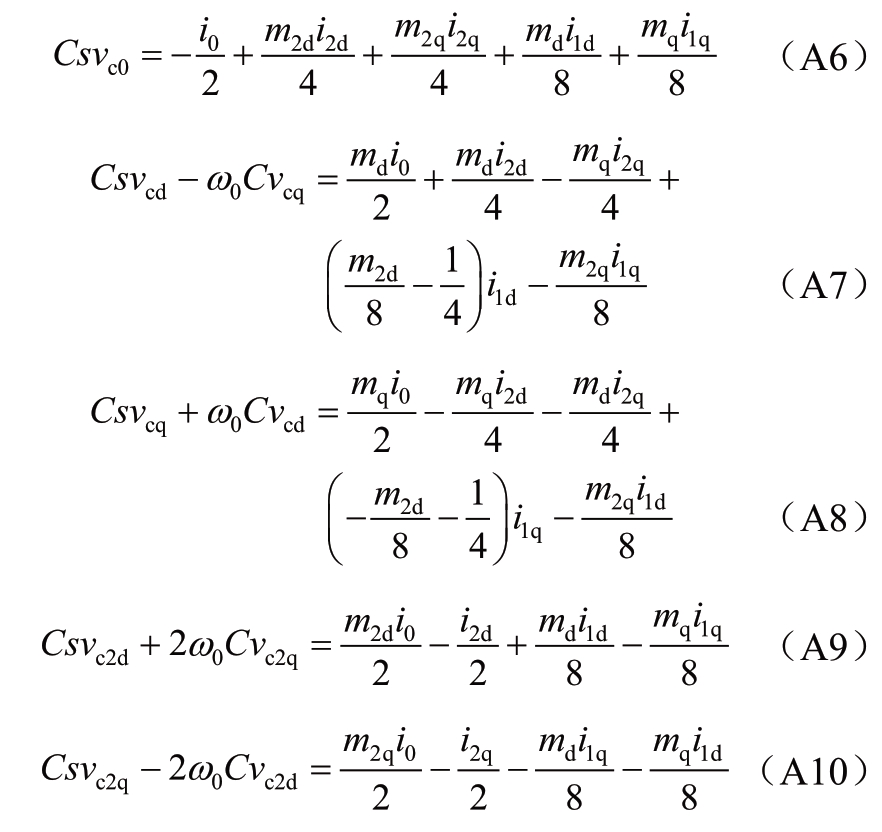
B 控制系统微分方程
锁相环(PLL)微分方程为:
外环控制器微分方程为:
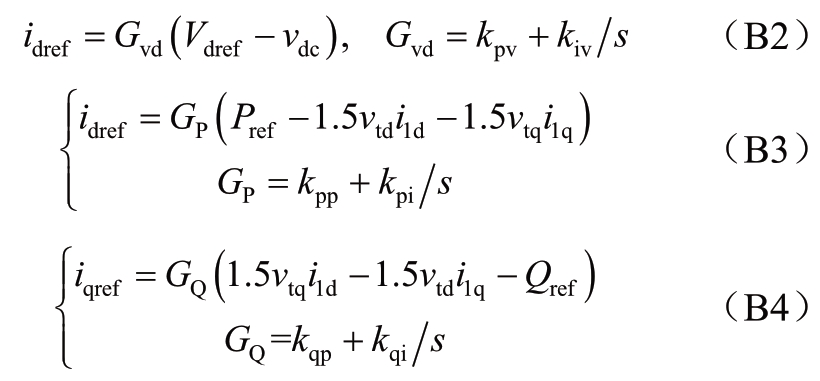
内环控制器微分方程为:
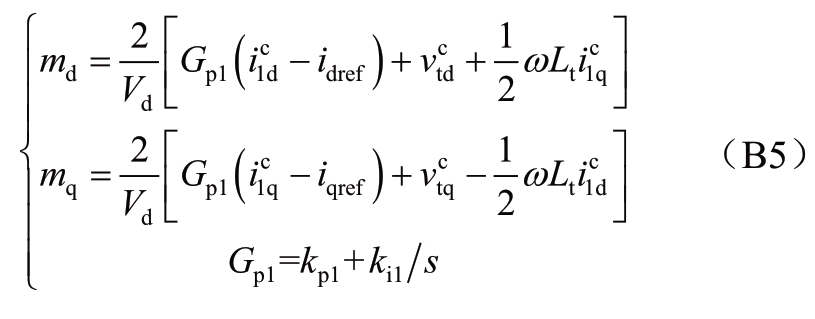
环流抑制控制器微分方程为:
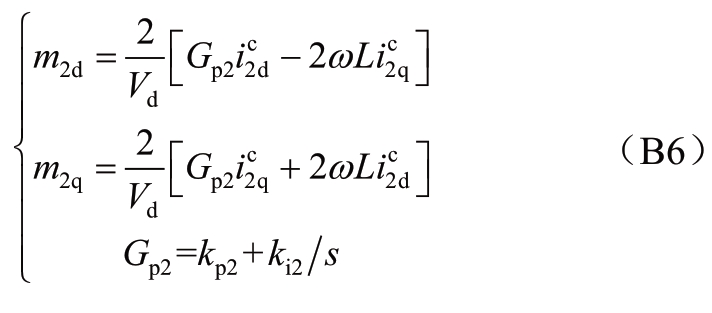
C MMC小信号模型的系数矩阵
C.1 功率控制站
式(13)中Δi0的各项系数为:
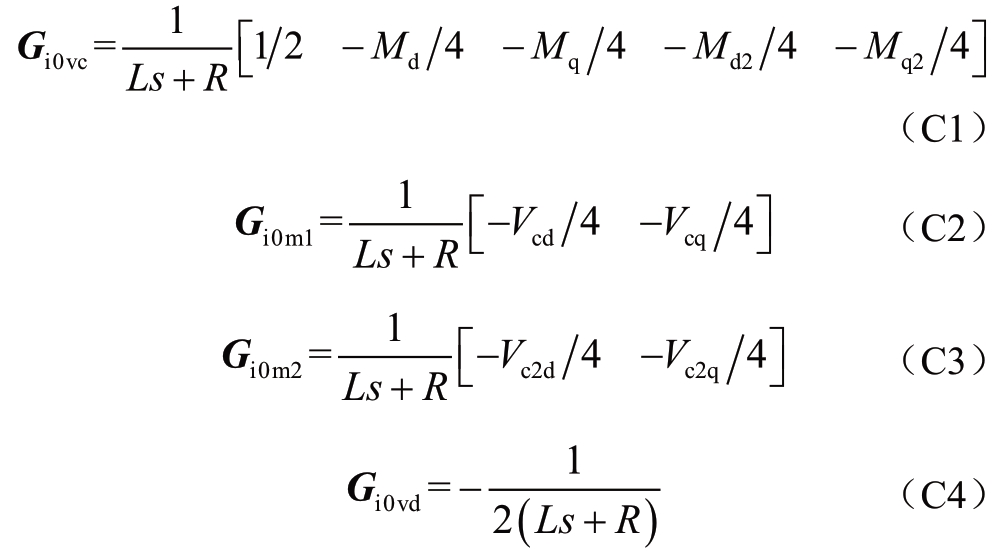
式(14)中Δi1的各项系数为:

式(15)中Δi2的各项系数为:

式(16)中Δvc的各项系数为:

C.2 直流电压控制站
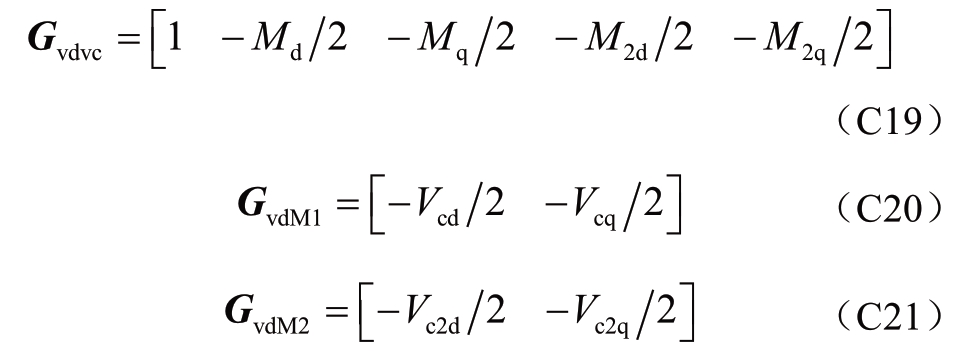
C.3 二倍频环流控制器小信号推导
以d轴二次调制信号m2d为例,
对(C22)线性化后可得
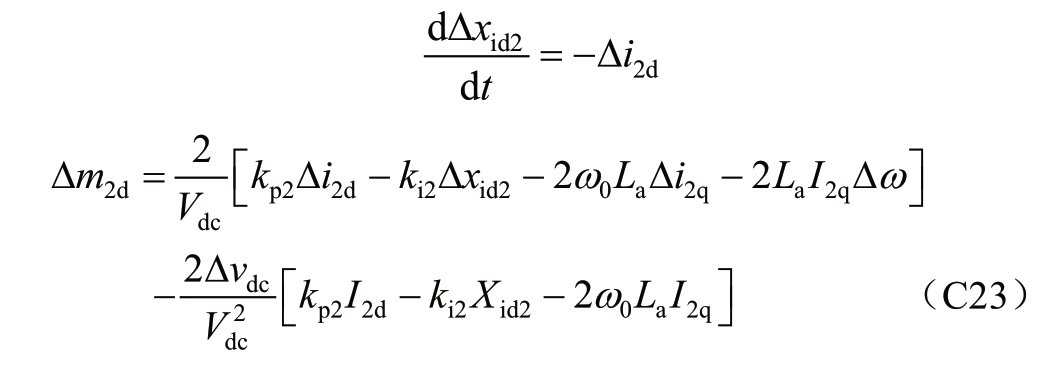
式中,大写字母表示状态变量的稳态值。
因为在稳态下,
且 I 2d =I 2q=0,所以(C23-2)为
将(C23-1)和(C24)变换到s域中,有
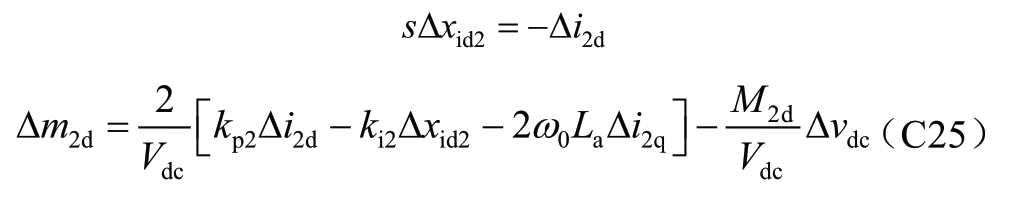
(C25-1)代入(C25-2)可得
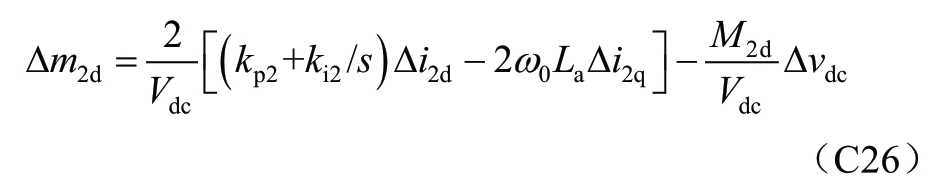
同理,q轴二次调制信号m2q,有
(C26)和(C27)写成矩阵形式,即
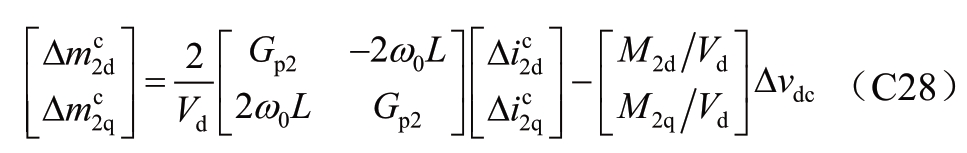
AC Impedance Model of Modular Multilevel Converter in Synchronous D-Q Frame
HAO Quanrui*, LI Dong
(Key Laboratory of Power System Intelligent Dispatch and Control of Ministry of Education, Shandong University, Jinan 250061, Shandong Province, China)
Abstract: Most existing equivalent impedance models of modular multilevel converters(MMCs)are based on the simplified models of the MMC system.The MMC system is divided into two parts based on the small signal models of MMCs:a control plant and a control system.The effects of PLL on the modulation and feedback signals between the two parts are considered.Based on this, the transfer function of each part is derived to develop the equivalent impedance model of MMC power control stations and MMC DC voltage control stations.Furthermore, the characteristics of the equivalent impedance of MMCs are investigated, and the effects of internal dynamics and PLL are analyzed.The equivalent impedance of DC voltage is derived from the coupling relationship of inner state variables.This is different form the existing model based on the power balance between AC and DC sides.Based on the derived impedance, the stability of an MMC system interfaced AC grid and with various control parameters is analyzed according to the general Nyquist criterion.The accuracy of the model and results is verified by performing simulations using Matlab/Simulink and PSCAD.
Keywords: modular multilevel converter(MMC); small-signal model; equivalent impedance; general Nyquist criterion(GNC)
作者简介:

郝全睿
郝全睿(1984),男,博士,教授/博导,研究方向为HVDC& FACTS、交直流混合电网。通信作者,E-mail:haoquanrui@sdu.edu.cn。
李东(1994),男,硕士研究生,研究方向为柔性交流输电、高压直流输电,E-mail:lmlidong@mail.sdu.edu.cn。
(责任编辑 张鹏)
