0 引言
随着中国能源消费的增长,环境污染问题也日益突出[1],调整能源发展布局、推进能源结构转型、发展清洁低碳能源、构建安全高效的现代能源体系是中国能源发展的重要战略布局[2]。由此,中国正大力发展太阳能、风能和潮汐能等多种新型绿色能源,但这类能源具有波动性,需要采用储能技术解决间歇性新能源消纳的问题以期达到平滑并网的目的。开发稳定、可靠、高效且容易大规模应用的储能系统是亟待解决的问题之一。目前,已有应用或正在研究的储能系统,包括抽水蓄能(pumped hydro energy storage,PHS)、飞轮储能(flywheel energy storage,FES)、相变蓄热储能(phase change heat storage,PCHS)、压缩空气储能(compressed-air energy storage,CAES)、超导储能(super-magnetic energy storage,SMES)和电化学储能(electrochemical energy storage,ECES)等[3]。其中,电化学储能系统因具有较高的功率和良好的能量可扩展性而广受关注。全钒液流电池(vanadium redox flow battery,VRB)又以其独特的优越性:可深度充/放电、功率和容量相互独立、使用寿命长和安全性高等,在可再生能源存储利用、电厂调峰调频、分布式能源等应用方面极具前景[4-6]。
目前,国内外针对电池构建的模型因机理不同可分为等效电路模型和电化学模型两类[7]。其中,等效电路模型利用理想电气元件模拟电化学过程,虽结构简单但不能较好且全面地反应电池充/放电的动态特性及对外等效特性。而电化学模型从电场、流场、浓度场和温度场等多场耦合机理出发,涉及全钒液流电池在工作过程中电荷、质量、动量和能量的守恒及电化学、反应动力学和流体力学等原理,精度较高。全钒液流电池的电化学模型能够直观描述实验中难以准确测量的关键参数,如过电势损耗、各价钒离子浓度和交换电流密度等关键运行参数在电极空间内的分布情况,适用于电池的材料优选及流道设计等[8]。Shah等人[9]建立了综合考虑电荷、质量、动量和能量守恒与电化学反应中动力学因素的VRB系统二维模型,并准确计算了过电势损耗、钒离子浓度以及交换电流密度在空间中的动态分布。Blanc和Rufer[10]建立了包含电化学、电气和流体力学等多物理场耦合的VRB系统模型,计算了电池的能量转化效率并提出了一种通过优化功率来提升VRB性能的方法。目前,针对全钒液流电池的负荷响应特性开展的研究工作较少。Tang[11]等人建立了浓度过电位与电解液流量的函数关系,提出了一种优化流量以提高系统效率的方法。Fu等人[12]建立了考虑电池浓度过电位和轴功的VRB模型,研究了电解液流量对电池效率的影响规律,提出了一种在变功率充/放电条件下的流量优化方法。Wang等人[13]在Fu等人[12]的基础上,进一步结合电解液流量对系统传质和温升的影响,建立了VRB系统的瞬态模型,提出了一种动态流量控制策略以提升系统性能。但上述研究在讨论泵功对系统性能的影响时,忽略了泵损对电池效率的影响,同时也未考虑电解液在管道内的流动状态。因此,本文基于自放电效应建立了全钒液流电池电化学模型和不同流动状态下包含泵损的泵功模型,研究了电池的充/放电形式和电解液流量对电池性能的影响规律,进而建立了微网负荷的优化调度模型,并提出了一种微网中逐时响应需求侧负荷波动的最优电解液流量计算流程和优化运行方法。研究结果可为全钒液流电池系统的优化运行提供理论参考。
1 全钒液流电池建模
全钒液流电池的正/负极电解液由质子交换膜分隔,并分别储存在正/负极储液罐中,通过蠕动泵驱动在系统中进行循环,电池的容量取决于电解液的体积和浓度,功率取决于单电池数量和电极板尺寸。图1为全钒液流电池的系统结构图。如图1所示,全钒液流电池的正极电解液为VO2+/VO2+电对,负极电解液为V2+/V3+电对。
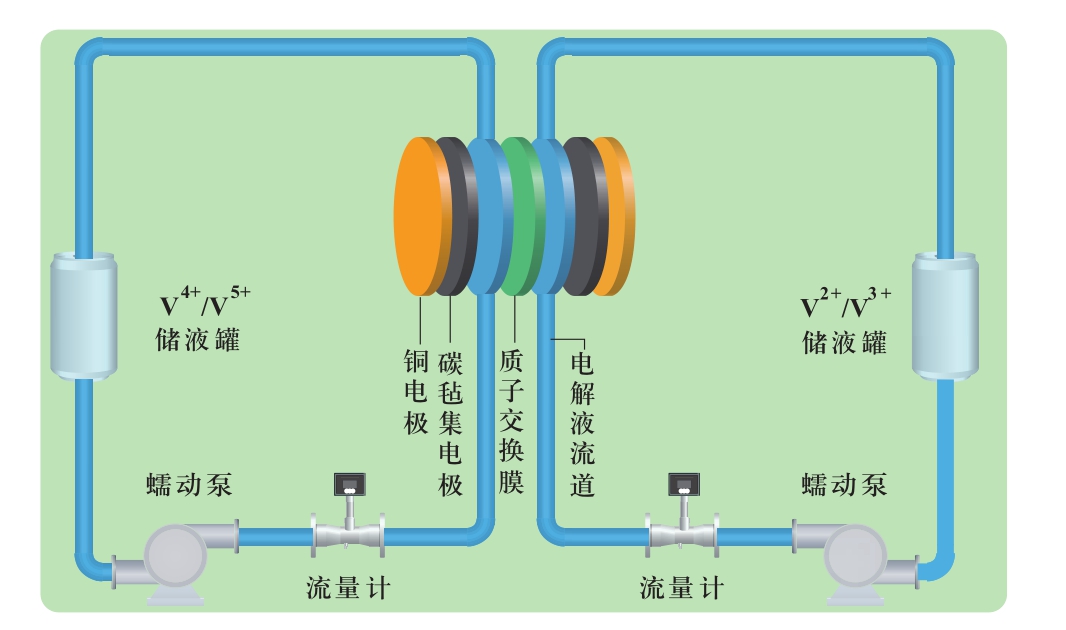
图1 全钒液流电池系统结构
Fig.1 The system structure of the vanadium redox flow battery
在电池的充/放电过程中,全钒液流电池除了在电极上发生主要的氧化还原反应之外,各价钒离子还会透过质子膜,分别在正/负极电解液中发生自放电反应,引起电池的浓度损耗。同时,蠕动泵作为全钒液流电池系统中唯一的耗功部件,其功率大小将直接影响电池的系统效率。本文基于自放电反应、Nernst方程、Butler-Volmer方程和Fick扩散定律建立了全钒液流电池的电化学模型,同时建立了不同流动状态下包含泵损的电池泵功模型。
1.1 全钒液流电池的电化学模型
全钒液流电池充/放电时的电极反应如下:
正极:
负极:
总反应:
由于钒离子会透过质子交换膜,引起正/负极电解液的掺混现象,使电池发生自放电反应[14-15],如式(4) —(7)所示。
正极
自放电:
负极
自放电:
根据Nernst方程,电池电势为
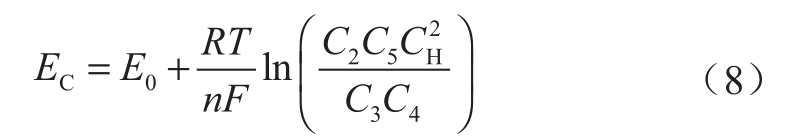
式中:E0是标准电极电势,V;R是理想气体常数,值取8.314 J/(mol·K);T是环境温度,值取298 K;F是法拉第常数,值取96485 C/mol;n是参与反应的电子数,值取1;C2、C3、C4、C5、CH分别是V2+、V3+、VO2+、VO2+、H+的离子浓度,mol/L。
根据反应式和Fick扩散定律[16],各种离子浓度的变化如下:
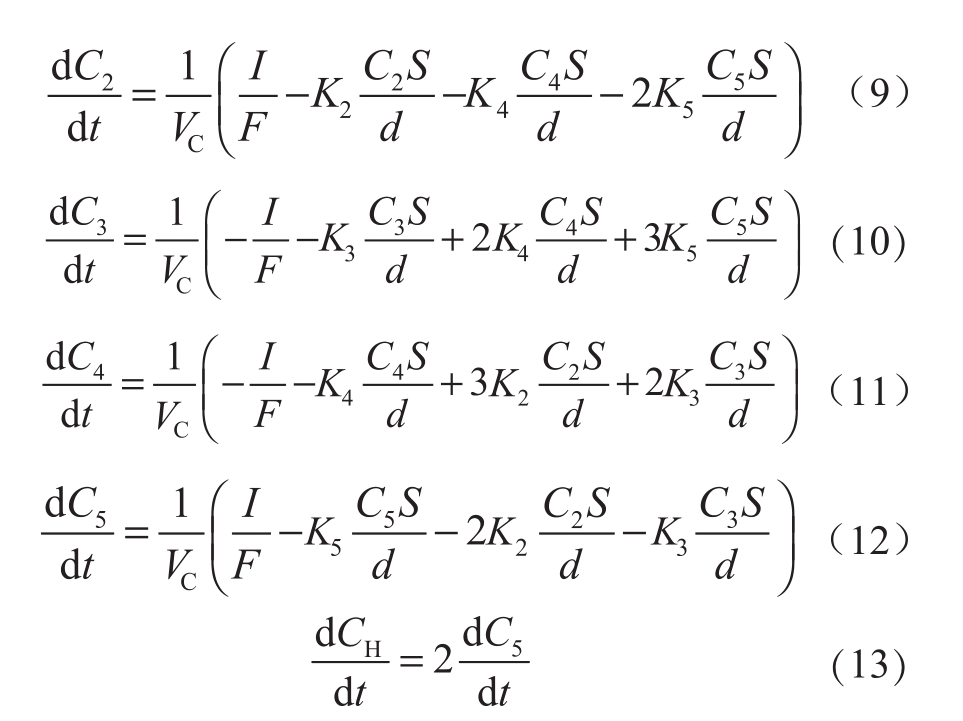
式中:Vc是正/负极电解液的体积,L;I是充放电电流,充/放电时分别为正/负,A;K2、K3、K4、K5分别是V2+、V3+、VO2+、VO2+的扩散系数;S是质子膜的面积,值取4.84×10-2 m2;d是质子膜的厚度,m。
电池荷电状态(state of charge,SOC)由式(14)定义。
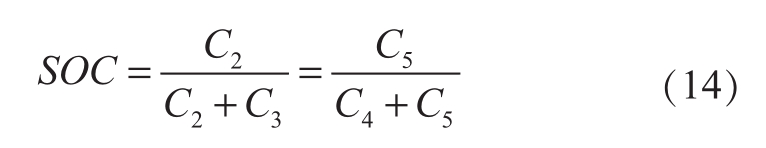
由于过电势的存在,电池实际电压Eb和热力学电势Ec并不相等[17]。电池过电势损耗主要由反应动力学引起的电化学极化损失、浓度梯度引起的浓度极化损失以及由膜、电解液、电极等引起的欧姆极化损失组成。其关系可表示如下[18]:
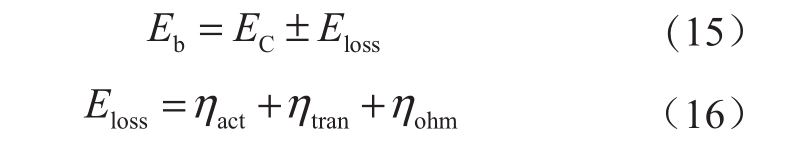
式中:ηact为电化学极化损失,V;ηtran为浓差极化损失,V;ηohm为欧姆极化损失,V。
其中,电化学极化损失可由简化的Butler-Volmer方程,即式(17) —(18)描述[17]。

式中:下标a和c分别表示阳极和阴极;j为静电流密度;j0为交换电流密度;β为传递系数,值取0.5;Δφ为电化学极化损失;Ka/c为阳极和阴极的标准速率常数;C0O为反应物的本体浓度;C0R为生成物的本体浓度。
浓差极化损失可由式(19)计算[12]。

式中:Q为电池电解液流量,m3/h;A为电极横截面积,m2;Cb为电解液的体积浓度,mol/L。
欧姆极化损失可由欧姆定律描述[19]:
式中,Rs为电池内部的等效比阻力。
1.2 全钒液流电池的泵功模型
全钒液流电池的电解液在系统中循环时需要由蠕动泵提供轴功,同时由于其流动时存在管道沿程压力损失、管道局部压力损失和流道中的压力损失,故需建立完备的电池泵功模型以评价电解液流量对系统性能的影响。
泵功可由式(21) — (23)计算[20]。
式中:P泵功为蠕动泵消耗总功率,W;P轴功为蠕动泵提供轴功,W;P泵损为蠕动泵额外耗功,W;H为泵的扬程,值取0.25 m;ρ为电解液密度,值取1354 kg/m3;η为泵效率,值取0.85;Δp为蠕动泵的全部压力损失,Pa;Δp1为蠕动泵在管道中的沿程压力损失和局部压力损失之和,Pa;Δp2为蠕动泵在流道中的压力损失;f为管道内流动的达西摩擦因数;L1为管道长度,值取2 m;D为管道水力直径,m;v为电解液在管道中平均流速,m/s;K为管道局部损失系数之和;u为电解液在流道内的平均流速,m/s;μ为电解液的粘度,值取4.928×10-3 Pa·s;L2为电极长度,值取0.1 m;ε为多空电极的渗透率,值取0.68。
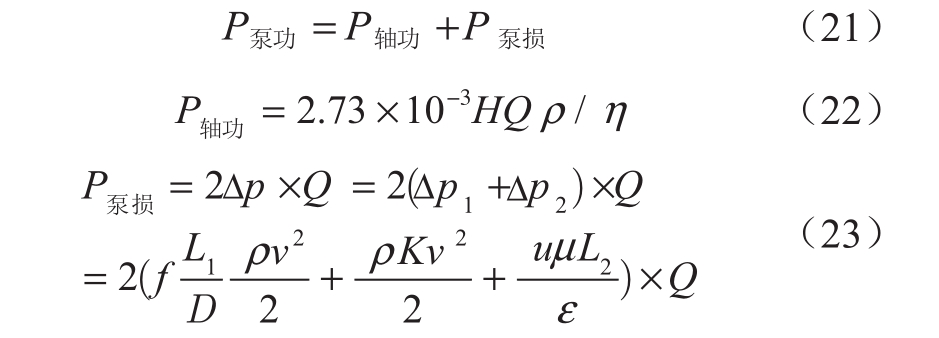
对于圆形管道内层流,达西摩擦因数的计算公式参见式(24)[20]。
式中,ReD为电解液在管道内流动的雷诺数。
对于圆形管道内湍流,达西摩擦因数可由光滑管的布拉修斯公式,即式(25)计算[20]。
依据雷诺数是小于或大于2300判别圆形管道内流动是层流还是湍流,分别引用式(24)和式(25)计算达西摩擦因数。
1.3 全钒液流电池的效率
全钒液流电池的能量效率可表示为
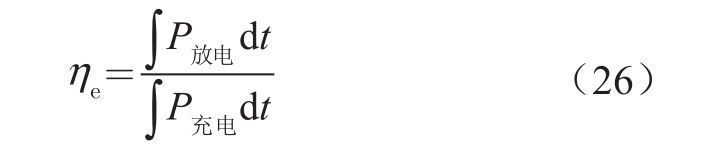
式中:P放电为电池的放电功率,W;P充电为电池的充电功率,W;ηe为电池的能量效率。
全钒液流电池的系统效率可表示为
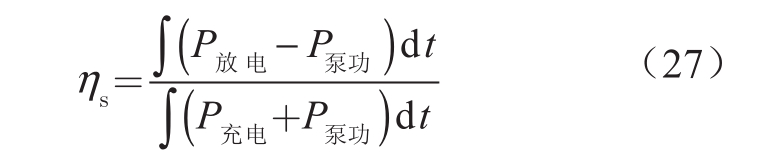
式中,ηs为电池的系统效率。
2 全钒液流电池关键参数影响规律
全钒液流电池系统较为复杂,影响系统性能的因素较多。其中,不同的充放电形式会影响单个充放电周期内电池电势、端电压和效率等电池性能参数的变化;同时,电解液流量会导致泵功和电池能量效率发生变化,进而影响电池的系统效率。因此,此节主要讨论全钒液流电池在一个完整充/放电周期内(从SOC为0时开始充电,至SOC为1时开始放电)恒电流/恒功率的充/放电形式和电解液流量对系统性能的影响规律。
2.1 充放电形式对电池性能的影响
分别采用电流为50 A的恒定电流充/放电形式和功率为21 W的恒定功率充/放电形式对电池进行充/放电模拟,研究不同的充/放电形式对电池性能的影响规律。
图2为不同充/放电形式下电池的电势和端电压随充/放电时间的变化曲线。由图可知:由于存在过电势损耗,在充电过程中,电池端电压比电势高;在放电过程中,电池端电压则比电势低。恒定电流充/放电时,充电时间与放电时间相近;恒定功率充/放电时,充电时间要明显长于放电时间。其原因为:电池的充/放电过程主要由钒离子浓度控制,离子浓度的变化越快,电池充/放电的速率越快。而离子浓度的变化速率主要取决于电流大小,和功率无直接关系,故电流越大,电池充/放电所需时间越短。此外,如图2所示,恒定电流时电池充/放电过程的电压损耗基本一致,而恒定功率时电池放电过程的电压损耗大于充电过程的电压损耗。这可以解释为:组成过电势损耗的3种极化损失均与电流有关,其中欧姆极化损失是主要电压损耗且与电流成正比,在电流变化范围不大的情况下,电化学和浓差极化损失变化很小。因此,可以近似地认为,电流越大,过电势损耗越大。

图2 充放电形式对电池电势和端电压的影响
Fig.2 The effect of different charging/discharging forms on the potential and terminal voltage of the battery
2.2 电解液流量对电池性能的影响
分别选取电解液流量Q为0.024、0.036、0.072、0.108、0.144和0.288 m3/h,采用电流为50 A的恒定电流充/放电形式,保持系统其它参数不变,研究电池电解液流量对系统性能的影响规律。
图3为泵功随流量的变化曲线。由图可知:随着电解液质量流量Q从0.024 m3/h增加至0.288 m3/h,P轴功相应由0.027 W增加至0.323 W,P泵损也相应由7.87×10-5 W增加至0.099 W,导致P泵功由0.027 W增加至0.422 W,P泵损占P泵功的比例由0.29%提高至23.48%。因此,在电解液流量较高时,不能忽略P泵损对P泵功的影响。
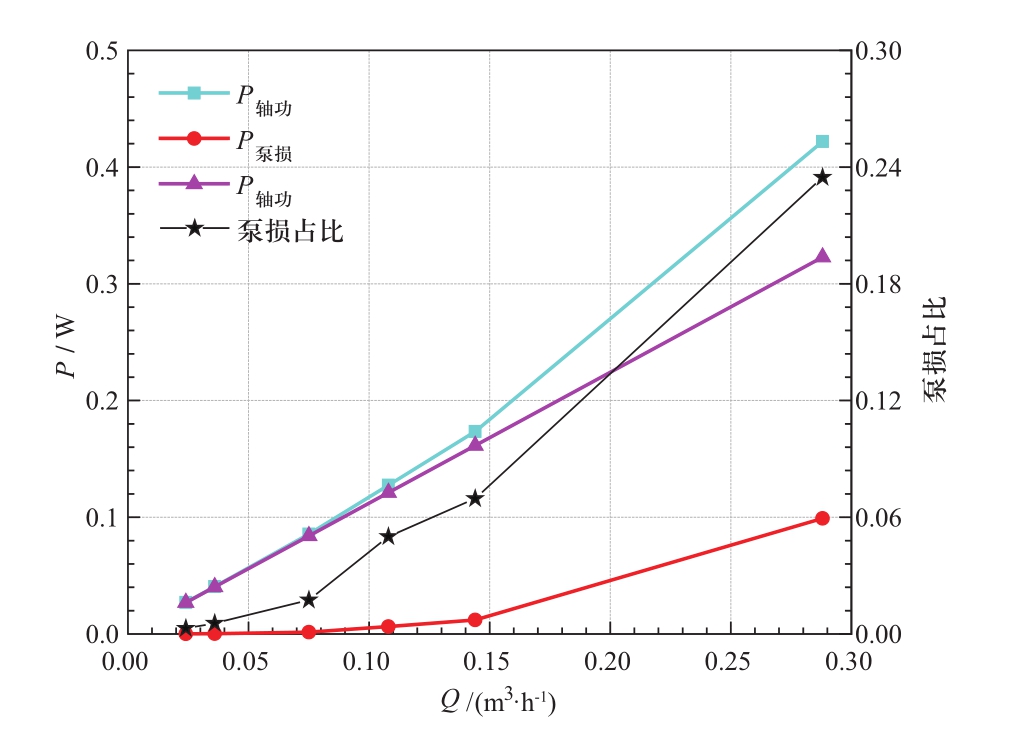
图3 电解液流量对泵功的影响
Fig.3 The effect of the electrolyte flow on the pump work
图4、图5和图6分别为不同电解液流量下电池电压随时间变化曲线、电池电压随SOC变化曲线以及电池功率随时间变化曲线。如图所示:在充电过程中,随着电解液流量的增大,浓差极化损失、端电压和电池功率减小;相反在放电过程中,随着电解液流量的增大,浓差极化损失、端电压和电池功率相应增大。分析可知:电池在工作过程中,不同价态的钒离子通过扩散到达碳毡集电极的表面并发生相关电化学反应。当离子的扩散速率低于在集电极表面的反应速率时,离子浓度差在空间中递减,即产生浓度梯度,进而产生浓差极化,形成浓差极化损失。电池浓差极化损失与电解液流量呈正相关。
图7为电池能量效率随电解液流量的变化曲线。由图可知:随着电解液流量Q从0.024 m3/h增加至0.288 m3/h,电池能量效率ηe由33.13%提高至35.77%,但其增长趋势逐渐放缓,即电解液流量的增加对于电池能量效率的提高是有限的。同时,电解液流量的增大会引起泵功的显著增加,进而使得电池的系统效率ηs降低。因此,恒定功率下,全钒液流电池存在最优的电解液流量可使电池的系统效率达到最高。
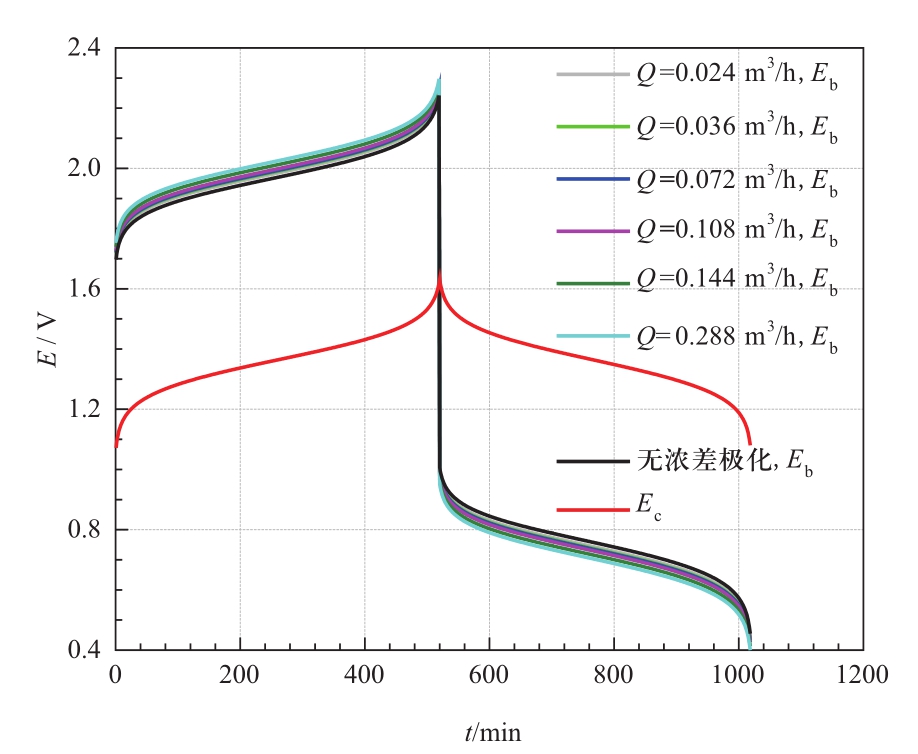
图4 不同电解液流量下电池电压随时间的变化
Fig.4 The change of the battery voltage with time under different electrolyte flow rates

图5 不同电解液流量下电池电压随SOC的变化
Fig.5 The change of the battery voltage with SOC under different electrolyte flow rates
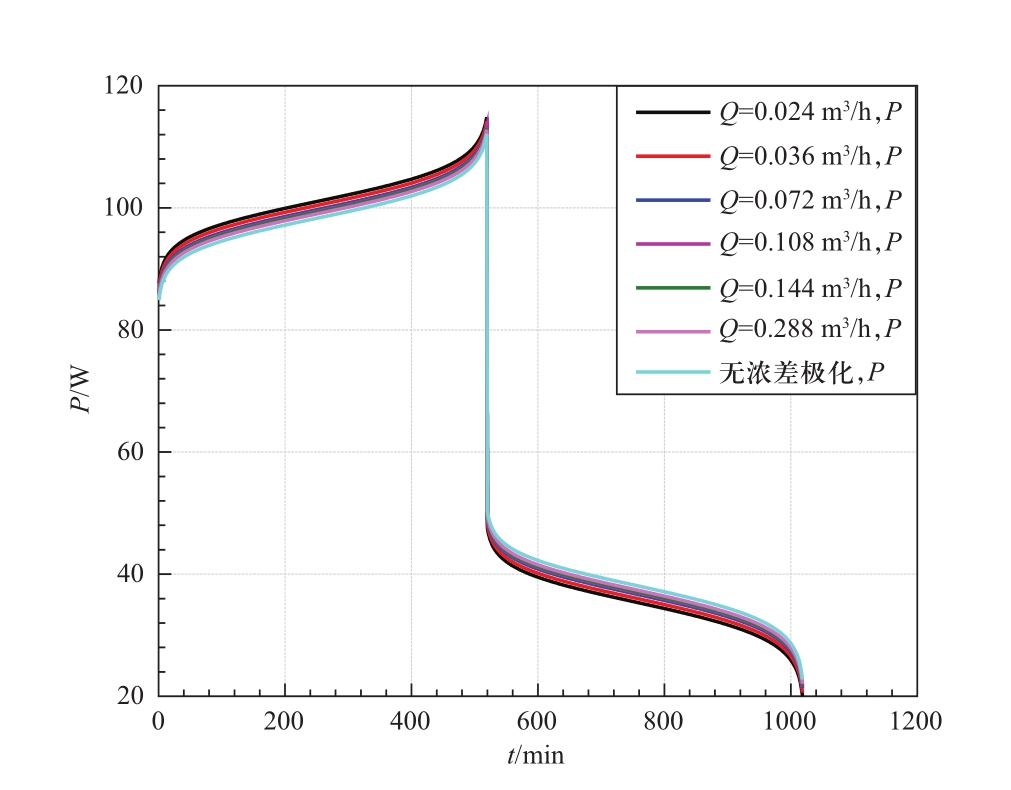
图6 不同电解液流量下电池功率随时间的变化
Fig.6 The change of the battery power with time under different electrolyte flow rates
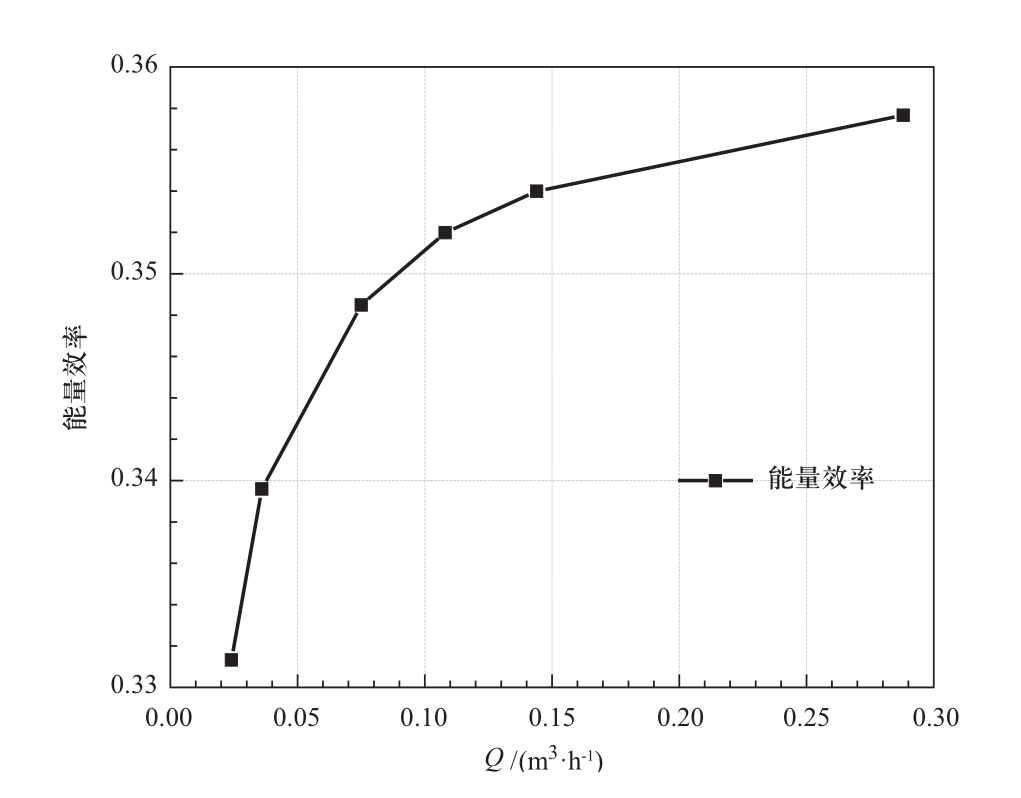
图7 电解液流量对能量效率的影响
Fig.7 The effect of the electrolyte flow rate on the energy efficiency
3 基于逐时流量控制的全钒液流电池优化运行方法
微网中全钒液流电池在实际运行过程中会随需求侧负荷的变化而实时调整充/放电功率,即很少存在恒定电流/恒定电压的充/放电情形。目前,在全钒液流电池运行过程中一般采用恒定流量的运行方法,未能充分考虑电解液流量对系统性能的影响。而恒定功率下,电池存在最优电解液流量可使得电池系统效率达到最高。此节建立了微网负荷的优化调度模型,同时提出了一种逐时响应需求侧负荷波动的最优电解液流量计算流程和优化运行方法。采用基于逐时流量控制的电池优化运行方法可获得较低的浓差极化损失和最高的系统效率。
3.1 微网负荷模型
将构建的全钒液流电池储能系统应用于一住宅小区,图8为基于历史数据拟合的微网24 h负荷曲线。
该微网采用燃气发电机组与太阳能光伏发电的联合发电形式。由于含可再生能源的分布式发电系统的出力通常具有较大波动性,故可利用储能系统进行“削峰填谷”,即当用户负荷小于分布式发电系统的供电功率时,储能系统储存多余的电能,而当用户负荷大于分布式发电系统的供电功率时,储能系统配合分布式发电系统进行供电,以达到平滑微网负荷的作用。

图8 微网负荷曲线
Fig.8 The power load of the microgrid
对于微网中的光伏发电系统,希望其能最大化可再生资源的利用率,以实现清洁供电需求;对于微网中的燃气发电机组,希望其能运行于较优工况区间以获得较高的发电效率,同时能减少出力的波动性,为微网提供更好的输出特性;对于微网中的全钒液流电池,希望其能尽量降低充/放电状态的切换频率以延长电池使用寿命。因此,建立了微网负荷的优化调度模型,并采用非线性规划算法对微网中各设备的出力进行优化。建立模型如下:
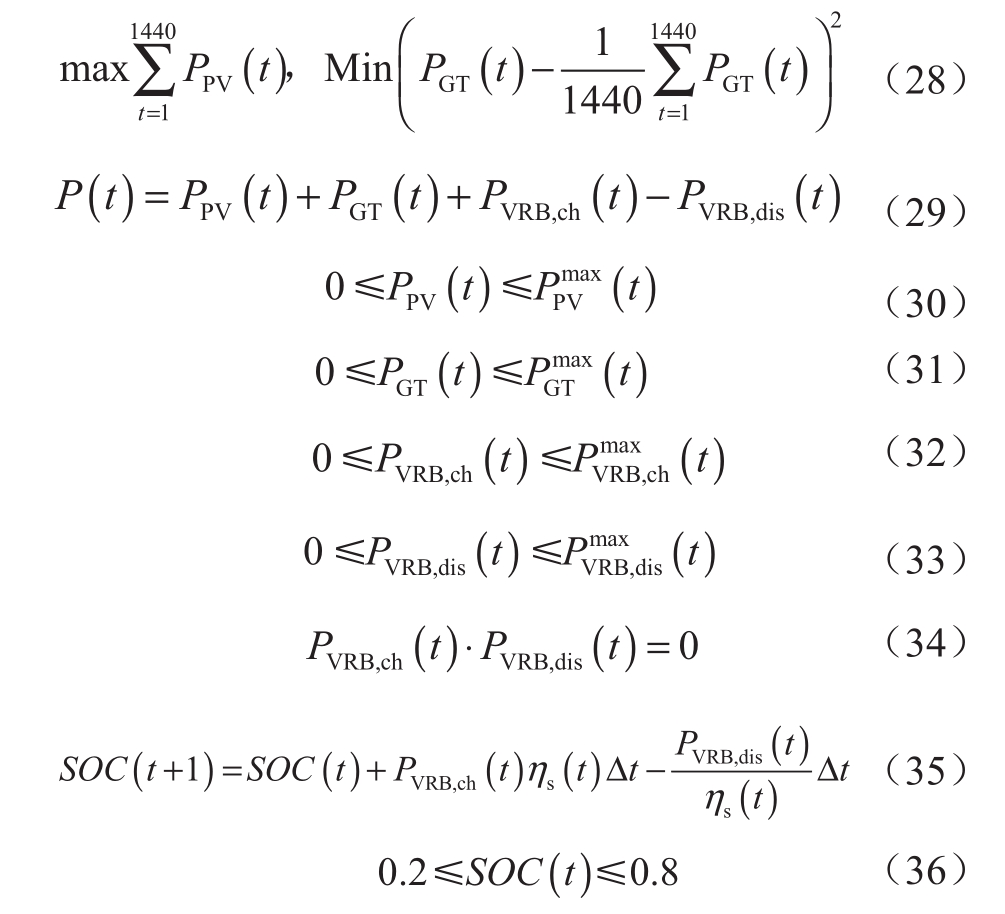
式中:P(t)为微网的用户需求负荷,kW;PPV(t)为光伏发电系统的出力,kW;PGT(t)为燃气发电机组的出力,kW;PVRB,ch(t)和PVRB,dis(t)分别为全钒液流电池的充/放电功率,kW。
图9为微网负荷优化前/后各设备的出力曲线。如图9(a)所示,燃气发电机组的功率随微网视在功率变化而实时变化,这使得燃气发电机组运行时偏离设计工况,其发电效率也远小于额定发电效率。同时,频繁的变负荷要求会使得燃气发电机组的调控更加复杂与困难。由图9(b)可知,微网负荷优化后,使用响应速率快的全钒液流电池对接负荷变化:在00:00至16:20期间和23:14至24:00期间电池处于充电状态,在16:21至23:13期间电池处于放电状态。同时燃气发电机组的出力保持50 kW稳定不变。该优化结果的实质是通过储能系统的容量裕度消纳微网的负荷变化,能很大程度上降低分布式发电系统的变负荷频率。
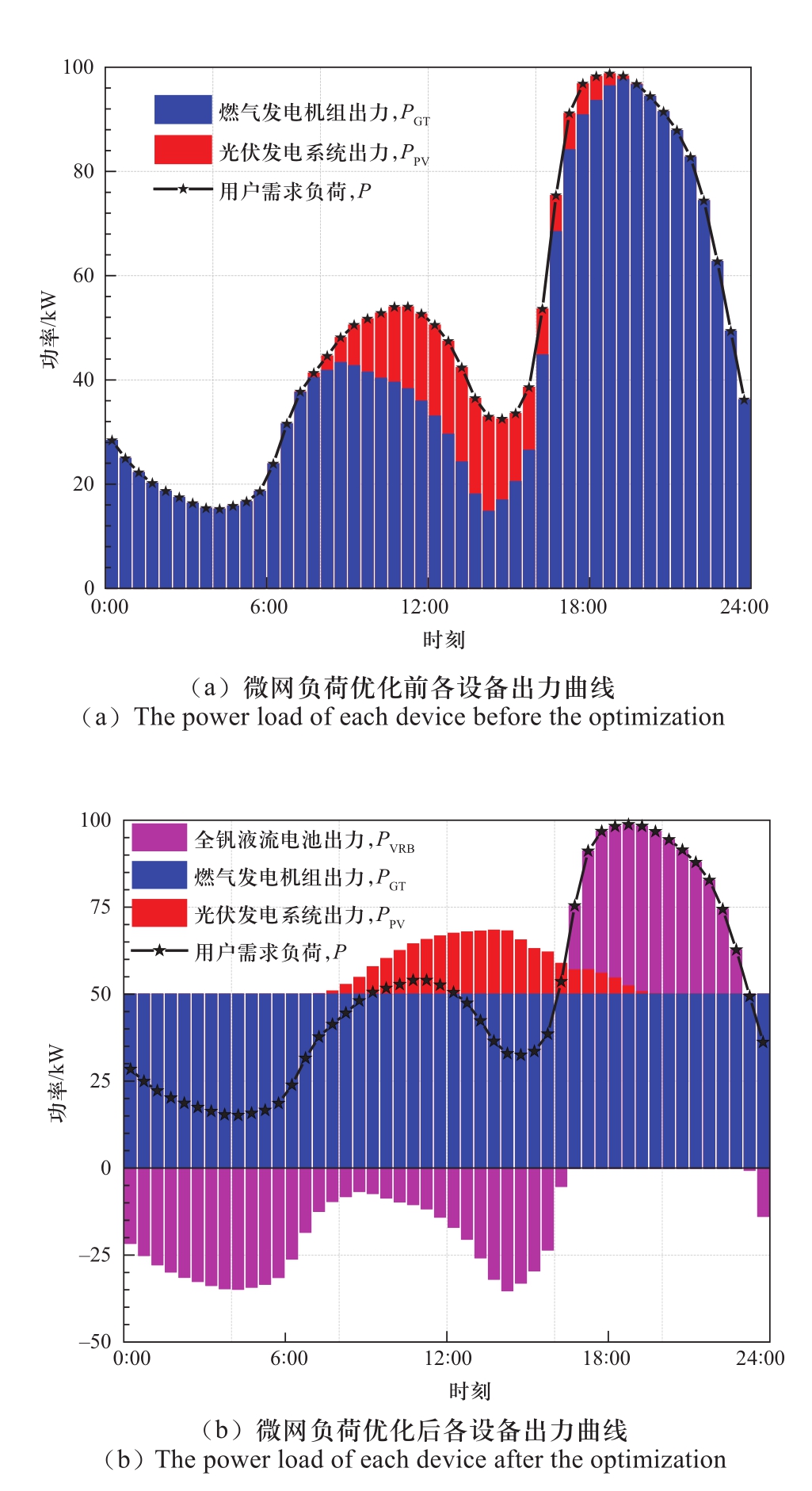
图9 微网中各设备出力曲线
Fig.9 The power load of each device in the microgrid
3.2 全钒液流电池优化运行方法
图10为基于逐时流量控制的全钒液流电池优化运行方法流程图。由图10可知,该方法的流程为:第一步,基于历史数据拟合微网负荷曲线;第二步,对微网负荷进行优化调度以获得全钒液流电池的出力曲线;第三步,根据出力需求计算每一时刻下电池的最优电解液流量;第四步,调整蠕动泵转速来实时控制电解液流量以获得较高的系统效率。其中,每一时刻下最优电解液流量的计算流程为:首先,由出力曲线确定电池的充/放电功率;其次,假定初始电流计算3类极化损失并假定初始电解液流量计算泵功,迭代计算t时刻下电池的最优电解液流量以使得系统效率达到最高;最后,计算t+1时刻电池的最优电解液流量。

图10 全钒液流电池优化运行方法流程
Fig.10 The process of the optimized operation method of the battery
3.3 系统关键参数的变化规律
图11、图12分别为微网中全钒液流电池的电压和SOC随时间变化的曲线。由于考虑了浓差极化损失,在充电过程中,无论负荷如何变化,电解液流量越大,浓差极化损失越小,端电压越小;相反在放电过程中端电压随电解液流量的增大而增大;在整个充/放电周期内,电池SOC值在0.26至0.76的范围内变化,一直位于0.2至0.8的安全稳定工作范围内,未发生过冲/过放现象。
图13为微网中全钒液流电池采用不同运行方法对系统性能的影响。由图可知,随着电池的电解液流量Q从0.024 m3/h增加至0.288 m3/h,电池的最大过电势损耗从212 mV减小至187 mV,但泵功随电解液流量的增大而增大,导致系统效率ηs随着电解液流量的增大呈先增大、后减小的趋势。采用实时优化电解液流量的运行方法可以获得较低的最大过电势损耗为189 mV,此时电池获得最高的系统效率为87.03%。因此,采用提出的基于逐时流量控制的全钒液流电池优化运行方法,可实现微网变负荷工况下电池电解液流量的实时优化控制,能够显著提高系统性能。
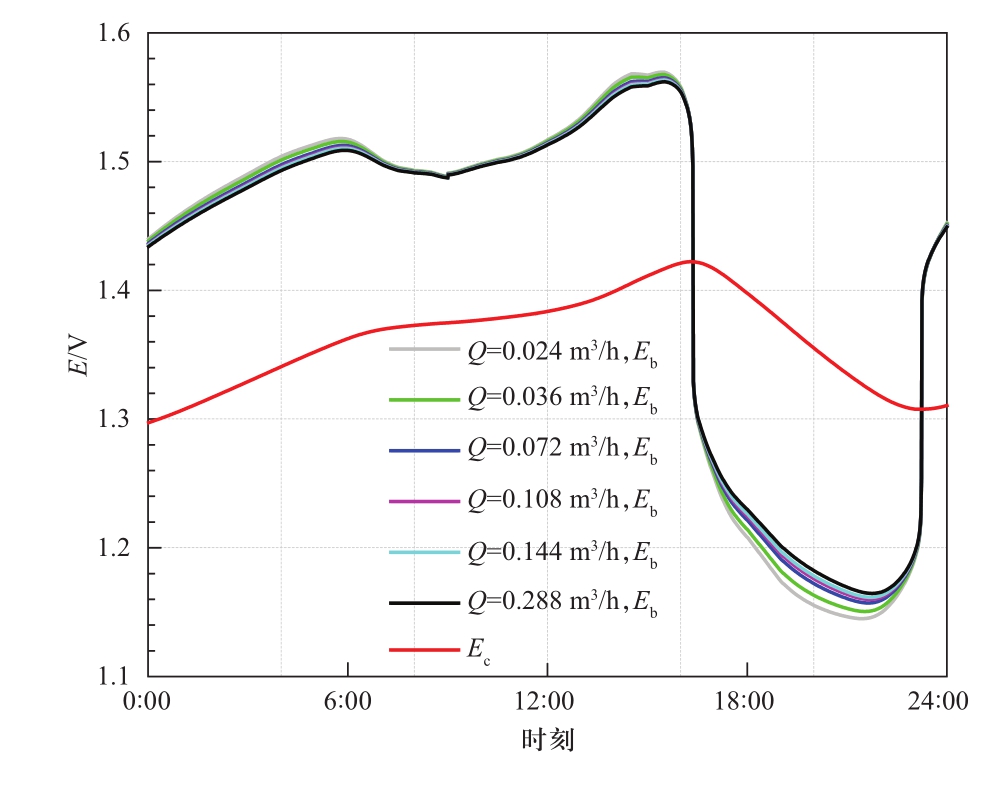
图11 微网中电池电压随时间的变化
Fig.11 The change of the battery voltage with time in microgrid

图12 微网中电池SOC随时间的变化
Fig.12 The change of SOC of the battery with time in microgrid
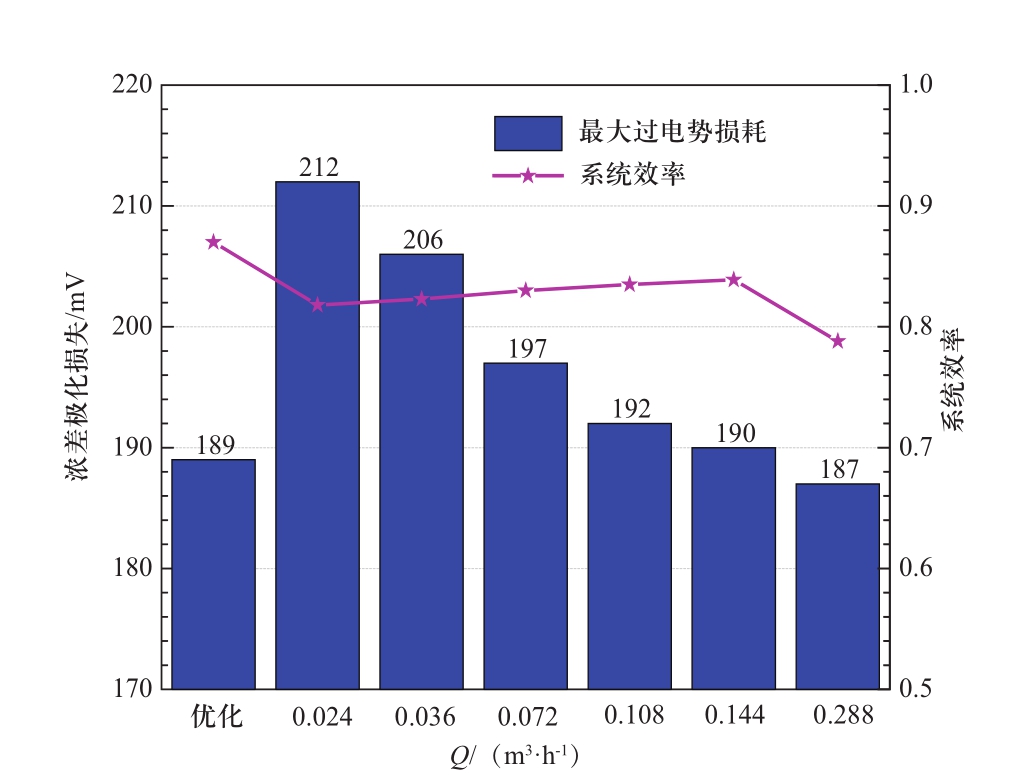
图13 全钒液流电池的不同运行方法对系统性能的影响
Fig.13 The effect of different operation methods of the vanadium battery in microgrid on system performance
4 结论
本文使用MATLAB基于自放电效应建立了全钒液流电池的电化学模型,研究了电池的充/放电形式和电解液流量对电池性能的影响规律,进而建立了微网负荷的优化调度模型,并提出了一种微网中逐时响应需求侧负荷波动的最优电解液流量计算流程和优化运行方法。具体结论如下。
1)恒定电流充/放电时,电池的充/放电时间、电压损耗相近;恒定功率充/放电时,充电时间明显长于放电时间,但其放电过程的电压损耗大于充电过程的电压损耗。
2)电解液流量越大,电池的能量效率越高,但泵功随之明显增加;恒定负荷下,选取合适的电池电解液流量可获得较高的系统效率。
3)相较于恒定流量的运行方法,采用提出的电池优化运行方法,可实现微网变负荷工况下电池电解液流量的实时优化控制,电池的系统效率可提高至87.03%。
参考文献
[1]中国环境状况公报[R].北京:中华人民共和国环境保护部,2015.
[2]能源发展“十三五”规划[R].北京:中华人民共和国国家能源局, 2016.
[3]国家电网公司“电网新技术前景研究”项目咨询组.大规模储能技术在电力系统中的应用前景分析[J].电力系统自动化,2013,37(1):3-8,30.
Consulting Group of State Grid Corporation of China to Prospects of New Technologies in Power Systems.An analysis of prospects for application of large-scale energy storage technology in power systems[J].Automation of Electric Power Systems, 2013, 37(1): 3-8, 30(in Chinese).
[4]Soloveichik G L.Battery technologies for large-scale stationary energy storage[J].Annual Review of Chemical and Biomolecular Engineering, 2011, 2(1): 503-527.
[5]Yang Z G, Zhang J L, Kintner-Meyer M C W, et al.Electrochemical energy storage for green grid[J].Chemical Reviews, 2011, 111(5): 3577-3613.
[6]Huang K L, Li X G, Liu S Q, et al.Research progress of vanadium redox flow battery for energy storage in China[J].Renewable Energy, 2008, 33(2): 186-192.
[7]Ulaganathan M, Aravindan V, Yan Q Y, et al.Recent advancements in all-vanadium redox flow batteries[J].Advanced Materials Interfaces, 2016, 3(1): 1500309.
[8]潘建欣,谢晓峰,王金海, 等.全钒液流电池模拟与仿真研究进展[J].化工学报,2011,62(S2):7-15.
Pan Jianxin, Xie Xiaofeng, Wang Jinhai, et al.Research progresses in modeling and simulation for all vanadium redox flow battery[J].CIESC Journal, 2011, 62(S2): 7-15(in Chinese).
[9]Shah A A, Watt-Smith M J, Walsh F C.A dynamic performance model for redox-flow batteries involving soluble species[J].Electrochimica Acta, 2008, 53(27): 8087-8100.
[10]Blanc C, Rufer A.Multiphysics and energetic modeling of a vanadium redox flow battery[C]//2008 IEEE International Conference on Sustainable Energy Technologies, November 24-27, 2008.Singapore.New York, USA: IEEE, 2008.
[11]Tang A, Bao J, Skyllas-Kazacos M.Studies on pressure losses and flow rate optimization in vanadium redox flow battery[J].Journal of Power Sources, 2014, 248: 154-162.
[12]Fu J H, Wang T, Wang X H, et al.Dynamic flow rate control for vanadium redox flow batteries[J].Energy Procedia, 2017,105: 4482-4491.
[13]Wang T, Fu J H, Zheng M L, et al.Dynamic control strategy for the electrolyte flow rate of vanadium redox flow batteries[J].Applied Energy, 2018, 227: 613-623.
[14]Sun C X, Chen J, Zhang H M, et al.Investigations on transfer of water and vanadium ions across Nafion membrane in an operating vanadium redox flow battery[J].Journal of Power Sources, 2010, 195(3): 890-897.
[15]Skyllas-Kazacos M, Goh L.Modeling of vanadium ion diffusion across the ion exchange membrane in the vanadium redox battery[J].Journal of Membrane Science, 2012, 399: 43-48.
[16]李明华, 范永生, 王保国.全钒液流电池充电/放电过程模型[J].化工学报, 2014,65(1):313-318.Li Minghua, Fan Yongsheng, Wang Baoguo.Model of charge/discharge operation for all-vanadium redox flow battery[J].CIESC Journal, 2014, 65(1): 313-318(in Chinese).
[17]Kazacos M S, Kazacos M.Stabilized electrolyte solutions,methods of preparation thereof and redox cells and batteries containing stabilized electrolyte solutions[P].U.S.Patent 6,143,443.2000-11-7.
[18]高鹏, 朱永明.电化学基础教程[M].北京: 化学工业出版社,2013:90-136.
[19]Aaron D, Tang Z J, Papandrew A B, et al.Polarization curve analysis of all-vanadium redox flow batteries[J].Journal of Applied Electrochemistry, 2011, 41(10): 1175-1182.
[20]张鸣远.流体力学[M].北京:高等教育出版社, 2010:331-355.
Optimized Operation Method of Vanadium Redox Flow Batteries Based on Microgrid Load Response
NI Jingwei, LI Mingjia*
(Key Laboratory of Thermo-Fluid Science and Engineering of Ministry of Education, School of Energy & Power Engineering,Xi'an Jiaotong University, Xi'an 710049, Shaanxi Province, China)
Abstract: The vanadium redox flow battery (VRB) is considered to be one of the most promising technologies for large-scale energy storage, as well as an effective method to solve the problems of peak regulation and frequency modulation of power grid and promote the consumption of intermittent renewable energy.In this study, the electrochemical model of the VRB system is formulated using MATLAB based on self-discharge effect to investigate the effect of the charge/discharge process and electrolyte flow rate on the battery performance of the VRB system.Furthermore, an optimized scheduling model for the load in a microgrid is formulated.An optimal electrolyte flow calculation model for real-time response to the demand side load fluctuations in a microgrid is also constructed, and an optimized operation method of the VRB system is proposed.Simulation results show that the overpotential loss of vanadium battery correlates positively with the current.When the electrolyte flow rate of the VRB system increased from 0.024 m3/h to 0.288 m3/h,the pump power consumed by the battery increased from 0.027 W to 0.422 W, resulting in an increase in the energy efficiency.Higher system efficiencies can be obtained under constant loads by selecting the appropriate electrolyte flow rate of the VRB system.The proposed optimized operation method of the VRB system can be employed to realize real-time optimal control of battery electrolyte flow in a microgrid under variable load conditions.Unlike the constant flow operation method, the system efficiency of the battery can be increased to 87.03%using the optimized operation method.
Keywords: vanadium redox flow battery; electrolyte flow rate;system efficiency; load response; optimized operation method
文章编号:2096-5125 (2019) 06-0608-09
中图分类号:TQ152
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.06.011
基金项目:国家自然科学基金项目(51806165)。
National Natural Science Foundation of China (51806165).
收稿日期:2019-07-05;修回日期:2019-08-12。
作者简介:

倪经纬
倪经纬(1996),男,博士研究生,研究方向为全钒液流电池,E-mail:nijingwei@stu.xjtu.edu.cn。
李明佳(1990),女,博士,教授,研究方向为能源的高效利用、新能源及储能技术等。通信作者,E-mail:mjli1990@xjtu.edu.cn。
(责任编辑 张宇)
