0 引言
近年来,随着动力电池技术的高速发展,全球电动汽车生产制造技术发展更加迅猛[1-2]。2018年全球电动汽车数量已经达到540万辆,较2017年增加64%,并且权威机构预测2019年全球电动汽车数量将达到850万辆[3]。中国是电动汽车增长量最大的国家,完善电动汽车充电设施是推动电动汽车发展的关键。
美丽城市的概念被提出后,城市配电网架空线被更换为电缆线路。电缆线路对地分布电容与配网中其他感性元件(如变压器、电抗器)发生感容耦合作用,局部配电网将发生谐波谐振现象,造成大面积谐波污染,不仅影响用户的用电质量,而且会导致电力设备异常运行[4-5]。电动汽车充电站内高频直流充电机多为整流型,且大功率充电机常使用PWM整流,其产生的谐波通过电缆接入配电网,在其他元件交互作用下,导致发生谐波谐振。
频率扫描法和模态分析法是当前用于电网谐波谐振分析的主要方法。频率扫描法可精确找到系统谐波谐振频率,但无法提供有效解决谐振问题的更多有用信息[6-7]。徐文远教授首次提出谐波模态分析法[8]用于分析谐振现象,并定义参与因子,不仅能快速计算电力系统谐波谐振频率,而且还能评估系统元件对谐振的影响程度。文献[9]提出一种改进模态分析法,结合虚拟支路法获得回路阻抗矩阵后对串联谐振进行分析与评估。文献[10]深入分析节点导纳矩阵的奇异性,提出了模态灵敏度分析法以度量系统元件参与谐振的程度,为谐波谐振评估提供了新途径。文献[11-12]考虑到长电缆对地分布电容的影响,基于模态分析法对偏远地区风电场并网谐振进行研究,结合参与因子和元件灵敏度值,找出了风电场滤波电阻损坏和风电机组停机的根源。文献[13]考虑高压直流落点谐波由高电压向低电压等级的传导特性和电缆对地分布电容,基于模态分析法提出多直流落点接入城市电网的谐波谐振分析方法。综上,模态分析法比频率扫描法更具优势,已被广泛应用。对城市电网电动汽车充电站通过电缆接入配电系统进而引起系统谐波谐振的问题却鲜有研究,文献[14]通过建立PWM整流型充电机动态小信号模型,获得了充电机闭环输入阻抗,但没有分析与电网的交互作用。
本文提出一种基于模态分析的电动汽车充电站并网谐振分析方法。首先,建立PWM整流型充电机闭环输入阻抗和电缆阻抗等效模型,以及由多个充电机构成的充电站并网模型;其次,使用模态分析法分析计算系统的谐振频率、节点的参与因子和元件的灵敏度值;最后,采用局部配电网实际数据,搭建PSCAD仿真模型,通过算例验证所提分析方法的可行性和正确性。
1 模态分析理论
1.1 模态分析法
模态分析法[8]的基本原理是针对一个多节点的电力系统网络,如果网络导纳矩阵已是或者接近奇异矩阵,意味着该系统发生了谐波谐振现象。
假设具有n个节点的电力拓扑在频率f时发生谐波谐振,根据电力系统谐波谐振分析方法,节点方程表示为
式中:Uf为频率f对应的节点电压向量;Yf为频率f对应的节点网络导纳矩阵;If为频率 f 对应的节点注入电流向量。
当电力系统发生谐波谐振时,网络中某些节点在频率f时的电压会非常高,这种现象的发生通常是因为网络导纳矩阵接近奇异。将导纳矩阵Yf分解为
式中:Λ表示n阶对角矩阵,对角元素为导纳矩阵的特征值;L、T分别表示左、右特征向量矩阵,并且满足L=T-1。
式(2)反映了电力系统网络内部结构特性,联立式(1)和式(2)可得
定义Vf = TUf为“模态电压向量”,定义Wf = TIf为“模态电流向量”,则式(3)可转化为
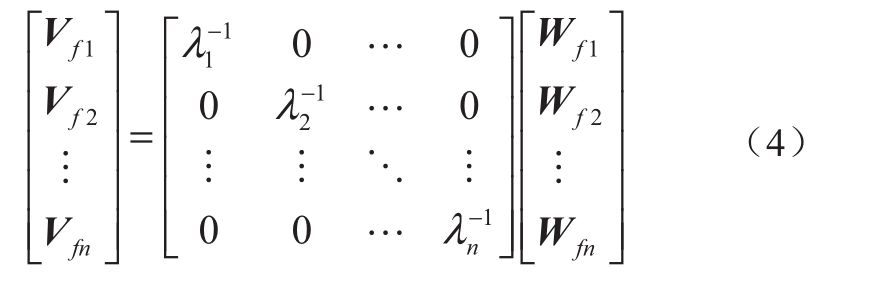
式中,λ1,λ2,…,λn表示矩阵Yf的特征值。
1.2 模态灵敏度分析理论
1.2.1 特征值对导纳矩阵Yf中元素的灵敏度
根据文献[10]可知,导纳矩阵Yf的特征值对网络元件的灵敏度等价于导纳矩阵Yf相对于同一个参数的灵敏度,其表达式为
式中:λk表示导纳矩阵Yf的第k个特征值;α表示网络元件参数,如电抗等;lk表示左特征向量中第k列元素;tk表示右特征向量中第k行元素。
1.2.2 特征值对网络元件的灵敏度
根据文献[10]可知,特征值对网络元件的灵敏度表达式为
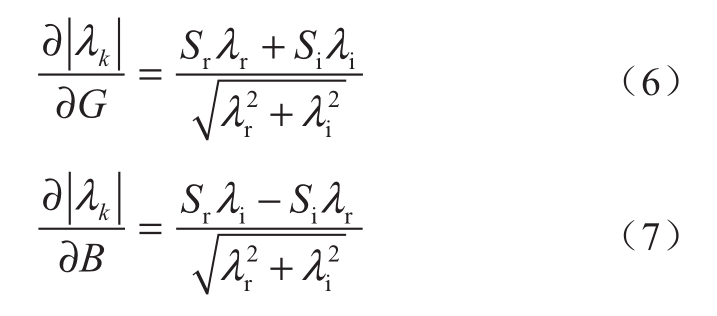
式中:λk = λr + jλi;Sλ,ii = Sr + jSi。
通常用等效阻抗zeq(zeq=R+jX)来表示导纳yeq(yeq=G+jB)。假定∂|λk|/∂G= β,∂|λk|/∂B= ω,则有
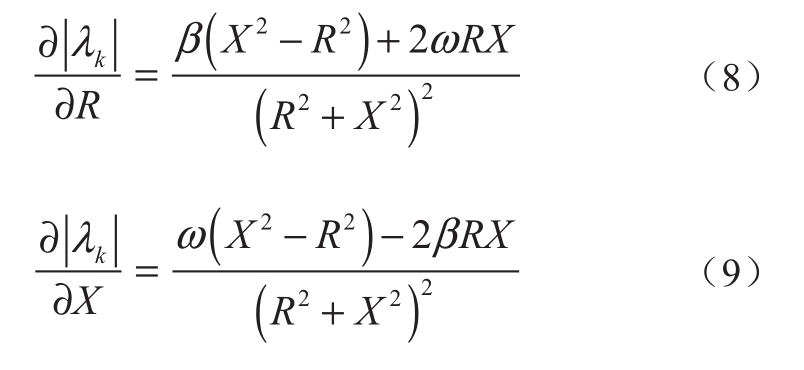
2 电动汽车充电站并网等效模型
2.1 电动汽车充电站并网模型
电动汽车充电站的功能是给汽车电池充电,主要由能量转换系统和控制系统组成,能量转换系统包括充电机、降压变压器和滤波装置等;控制系统包括充电机控制、电能监控和充电计费等系统。电动汽车充电站并网拓扑如图1所示。
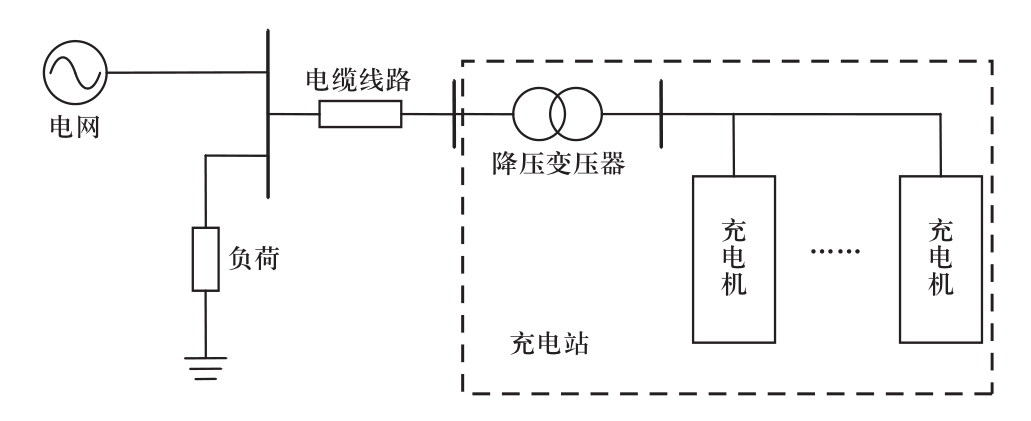
图1 电动汽车充电站并网拓扑
Fig.1 Topology of grid-connected charging station
电动汽车充电站由多台高频整流充电机构成,含PWM整流器和滤波器等电力电子装置,其工作原理是整流器对输入的三相交流电整流,经过滤波器滤波后为电动汽车电池充电。对电动汽车充电站进行并网谐振分析,需先建立单台PWM整流型充电机输入阻抗模型。
2.2 充电机并网输入阻抗模型
PWM整流型充电机拓扑如图2所示,PWM整流型充电机控制系统结构如图3所示。因PWM整流型充电机会产生谐波,仅采用并网电流控制的单环控制难以保证系统的稳定。因此,需采用电流内环与电压外环控制相结合的双闭环控制[15-16]来保证电力系统的稳定运行。
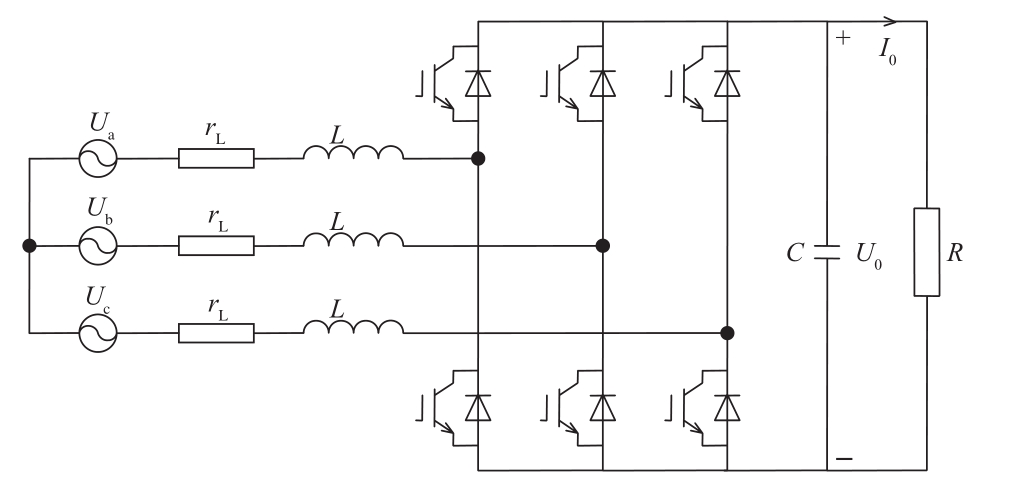
图2 PWM型充电机拓扑结构
Fig.2 Topology of PWM charging pile
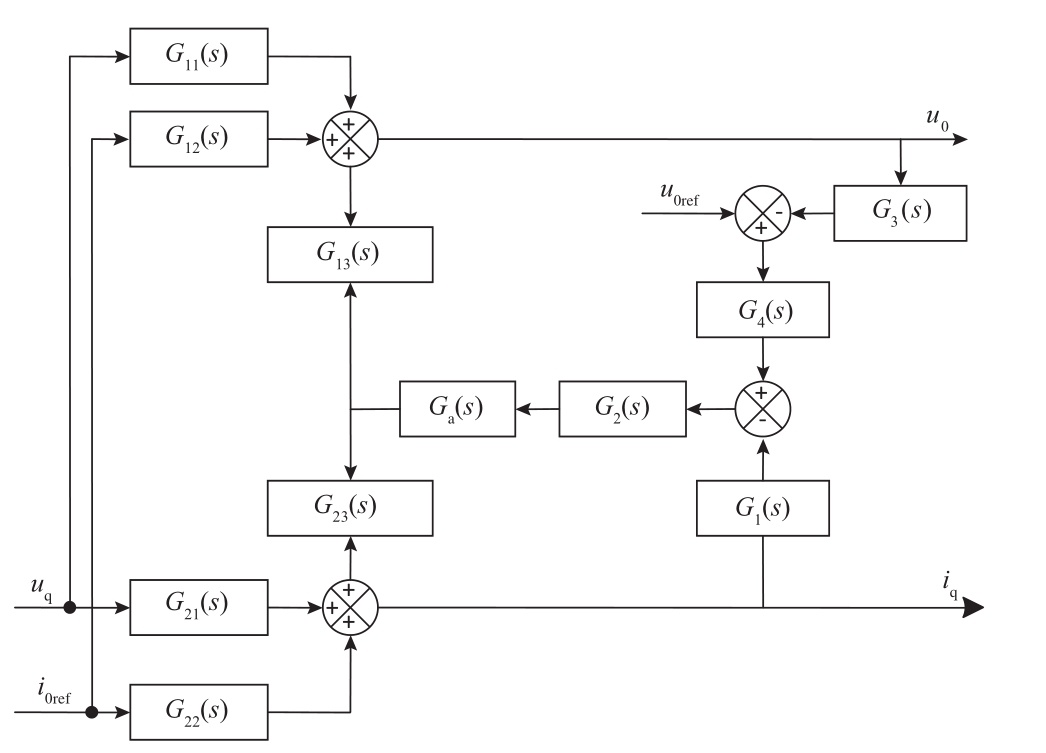
图3 PWM整流型充电机的控制框图
Fig.3 Control block diagram of PWM charging pile
图3中,G1、G2、G3、G4和Ga分别表示q轴电流采样系数、电流环路控制器增益、输出电压采样系数、电压环路控制器增益以及PWM调制器增益。G11、G12、G13、G21、G22和G23分别表示系统传递函数,具体表达式如下。
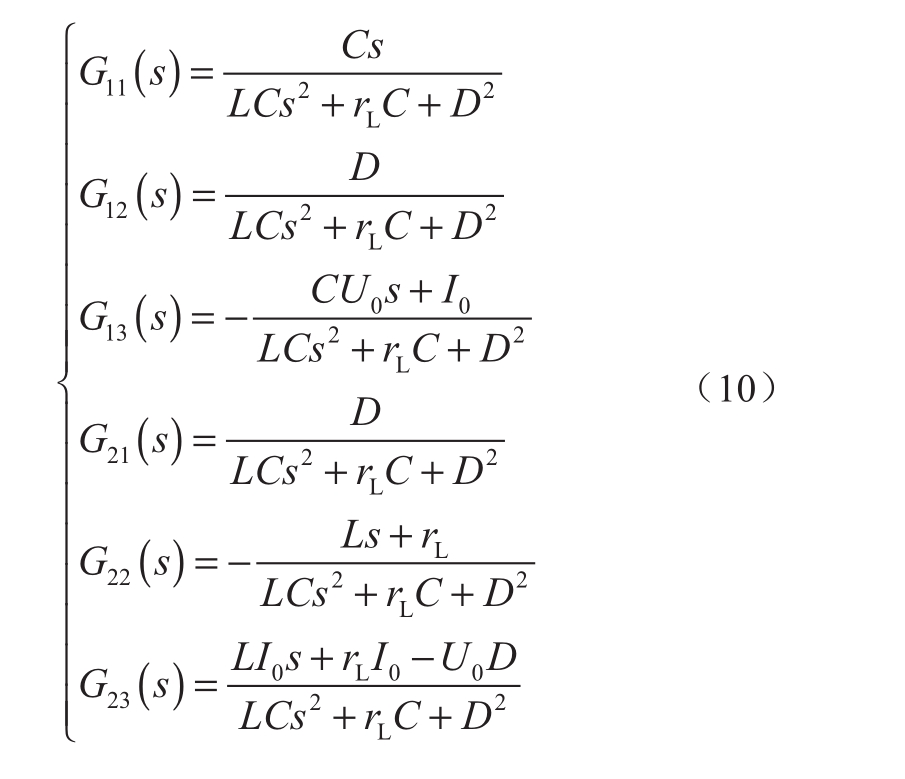
其中
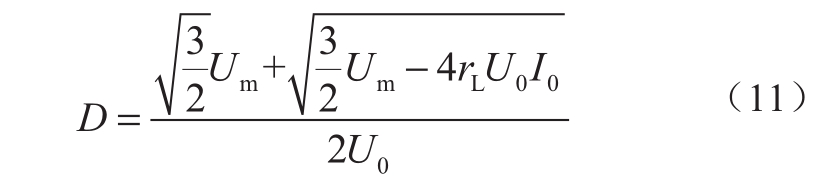
式中:rL为电感寄生电阻;L为交流侧电感;C为直流侧母线电容;Um为三相正弦电压最大值;U0为直流输出电压;I0为直流输出电流;
由图3及参数定义,根据Mason定理[14]可以得出单台PWM整流型充电机输入阻抗:

其中

2.3 电缆线路等效模型
电缆线路的对地分布电容与城市配电系统谐振问题密不可分[17-18]。因此,进行谐振分析前需建立城市配电系统电缆线路等效阻抗模型。
图4表示电缆线路的等值电路,ZL表示电缆线路阻抗,YL表示对地电容容抗。
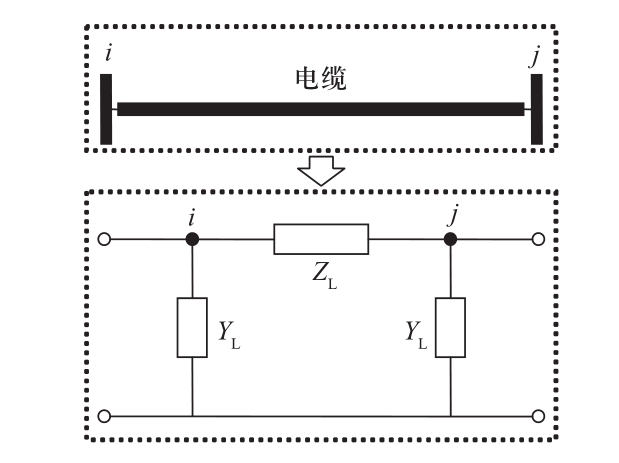
图4 电缆线路等值电路
Fig.4 Equivalent circuit of cable
根据图4的电缆线路等值电路,采用分布式参数模型可得ZL和YL的表达式。
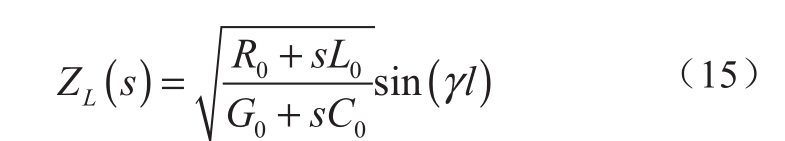
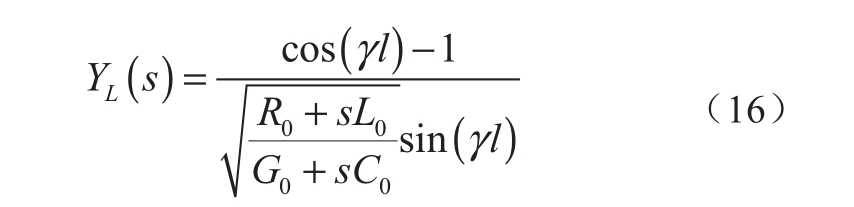
式中:R0、L0、G0和C0分别表示电缆线路单位长度等效电阻、电感、电导和分布电容;l表示电缆线路长度;γ表示电缆线路的传播系数,其表达式如式(17)所示。
3 基于模态分析法的充电站并网谐振分析
根据前文建立的单台PWM整流型充电机输入阻抗和电缆分布式参数阻抗模型,建立含多台PWM型充电机的电动汽车充电站并网模型,如图5所示。
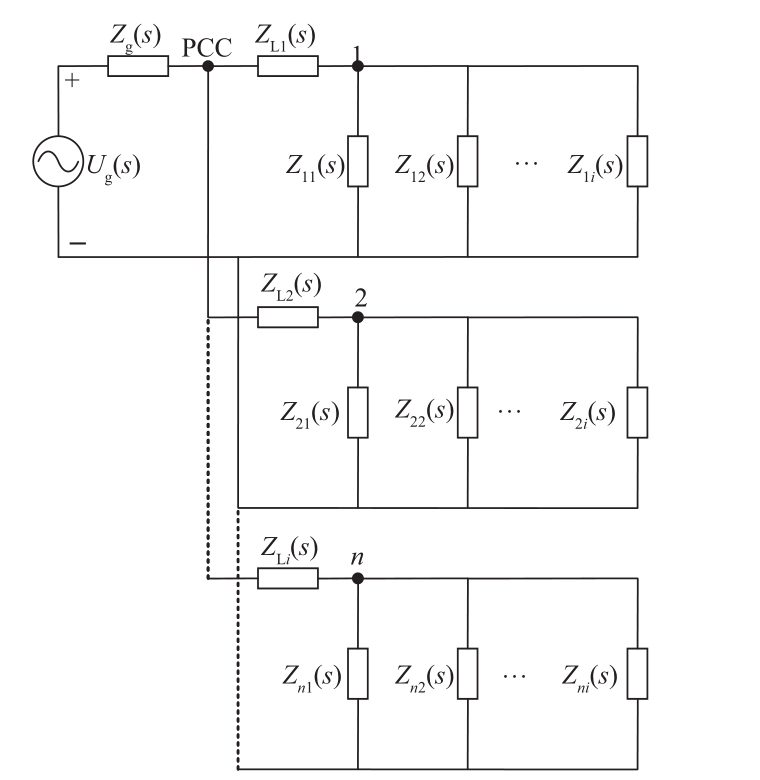
图5 电动汽车充电站并网模态分析模型
Fig.5 Modelling for grid-connected modal analysis of charging station
根据前文建立的模型,基于模态分析法的电动汽车充电站并网谐振分析的流程如下:
1)依图5的电动汽车充电站并网模型,结合各元件阻抗模型,得出网络节点导纳矩阵Yf(s);
2)将节点导纳矩阵Yf(s)按式(2)分解,得到矩阵左特征向量L、对角矩阵Λ和右特征向量T;
3)计算对角矩阵Λ中元素的倒数即为网络的模态阻抗,同时绘制其模态阻抗曲线;
4)根据模态阻抗曲线及模态阻抗峰值找出对应模态,进而确定谐振频率,并按式(8)计算节点参与因子,分析与评估系统谐波谐振现象;
5)按照式(14)~式(18)计算网络元件的归一化灵敏度值,分析元件对系统谐波谐振的参与程度;
6)根据上述绘制的模态阻抗曲线、节点参与因子和元件灵敏度值,为配电网规划提供决策依据。
4 算例分析与实测验证
4.1 算例概述
以某局部配电网为算例,该局部配电网内包含3座(1#、2#、3#)电动汽车充电站,站内充电机均为PWM型,数量均为6台,配电网线路均为电缆线路,其结构如图6所示。电动汽车充电站并网相关参数如表1所示。
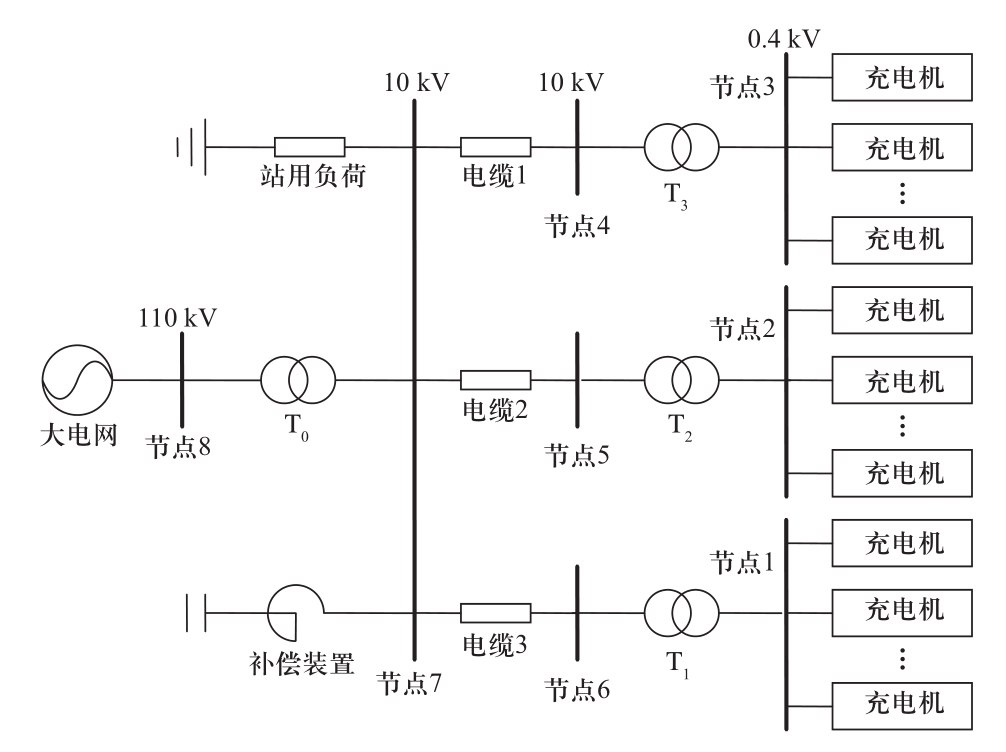
图6 含电动汽车充电站的局部配电网
Fig.6 Local distribution network with EV charging station
表1 仿真算例参数
Table.1 Parameters of simulation
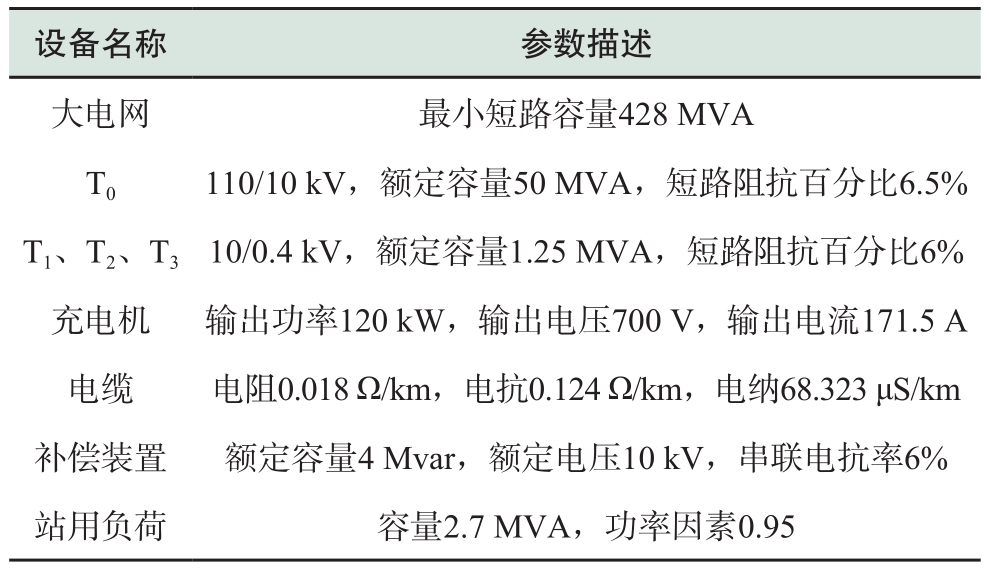
由于电动汽车充电站位置不同,敷设的电缆长度也不同,电缆1(节点4-节点7)长度为4.45 km,电缆2(节点5-节点7)长度为5.62 km,电缆3(节点6-节点7)长度为4.96 km。
4.2 模态分析结果
根据局部配电网拓扑及元器件参数,在PSCAD仿真平台中搭建仿真模型。基于模态分析法对该局部配电网进行谐振分析,仿真时采用标幺值,仿真结果如图7所示。
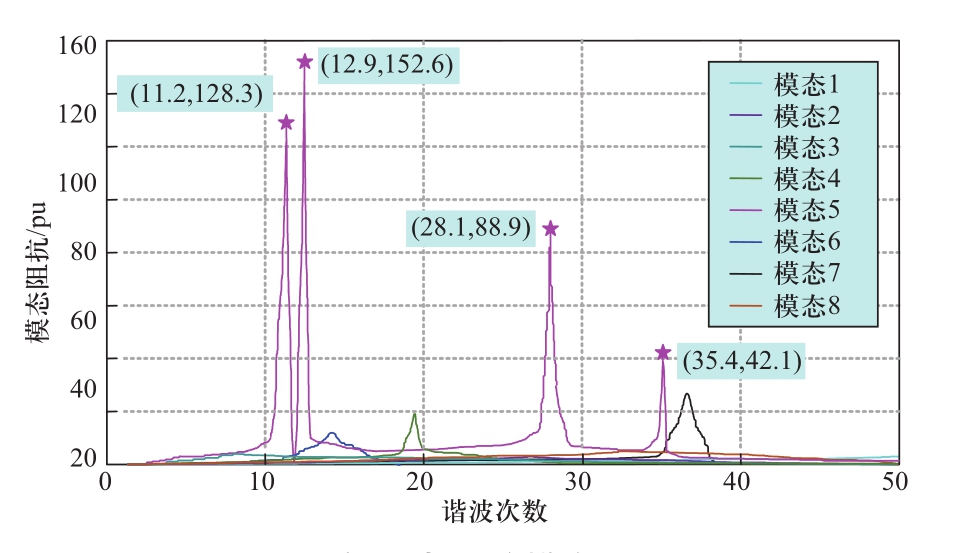
图7 局部配电网的模态分析结果
Fig.7 Modal analysis results of local distribution network
根据图7模态分析结果,谐振模态5包含4个谐振频率(11.2 pu、12.9 pu、28.1 pu、35.4 pu),可认为模态5是关键模态,对应的谐波次数可近似为11次、13次、28次和35次,由于实际系统中偶次谐波出现几率较低,28次谐波谐振可忽略。除去28次谐波,局部配电网各节点在其他3种频率下的参与因子如表2所示。
表2 局部配电网的谐振信息
Table.2 Resonance information of the distribution network
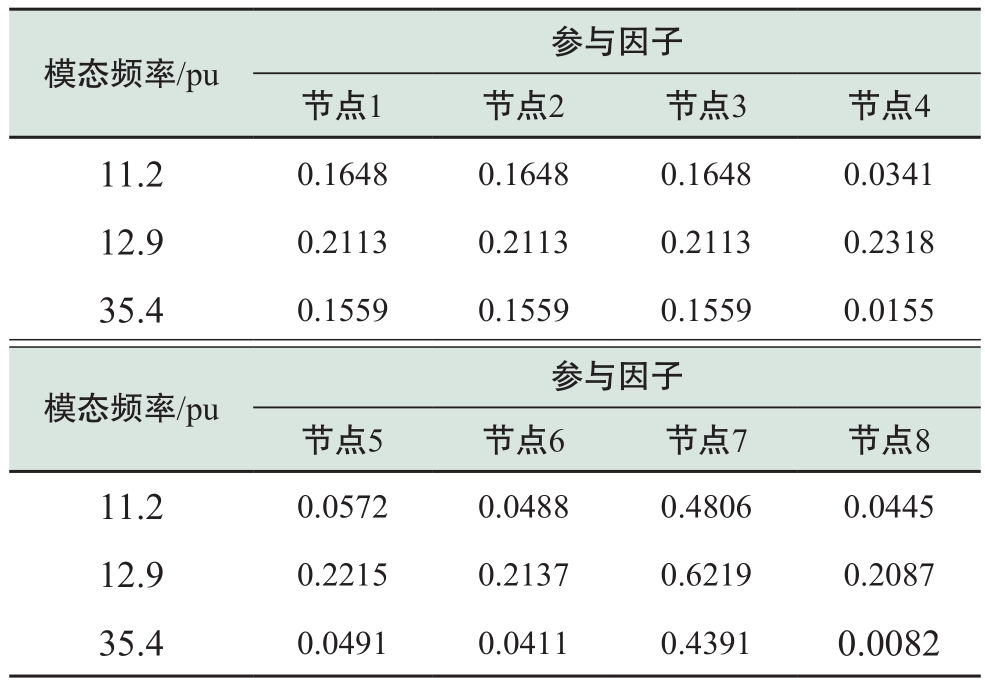
由表2可知,关键模态下3种谐振频率对应的节点7的参与因子最大,意味着该局部配电网中出现11次、13次和35次谐波,节点7最容易发生谐波谐振,也最容易观测到谐波谐振,因此,节点7被定义为该局部配电网的谐振中心。
若配电系统出现13次谐波,除了节点7外其他节点的参与因子数值相差甚小,意味着13次谐波在每个节点均有可能发生谐振,谐波电压可能超过国家标准限值。
由于仿真构建的3座电动汽车充电站及其配电变压器的参数一致,因此表2中节点1、节点2和节点3的参与因子始终保持一致。
另外,为识别配电系统元件对谐波谐振现象的影响程度,本文求取关键模态下模态阻抗对配电网元件参数的归一化灵敏度,如图8所示。
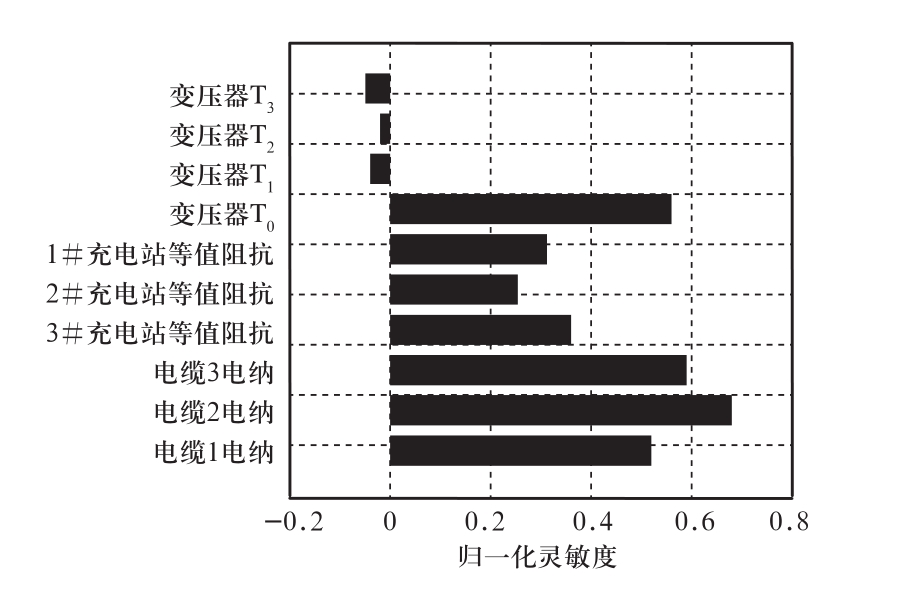
图8 配电网元件归一化灵敏度值
Fig.8 Element normalized sensitivities of distribution network
由图8可知,元件的归一化灵敏度值有正有负,度量了元件参数对系统谐振的影响程度。配电变压器T1、T2和T3灵敏度值为负,说明配电变压器参数逐渐变大时,关键模态的关键特征值会对应增大,关键模态导纳减小,则系统谐振程度就会对应减弱,有利于配电网稳定运行。而其他元件灵敏度值为正,说明元件参数逐渐减小时,关键模态的关键特征值会对应减小,关键模态导纳增大,则系统谐振程度就会对应增加,不利于系统运行。尤其是电缆和主变压器T0,由于电缆对地电容大,使得电缆1、电缆2和电缆3极易与主变压器T0发生感容耦合而引起11次、13次谐波放大。
另外,电动汽车充电站的等值阻抗值得重点关注,其灵敏度值较高,充电站的等值参数对谐振的影响也不容忽视。
4.3 实测数据对比分析
结合局部配电网实际数据,该局部配电网中电动汽车充电站由变电站内10 kV母线供电,该变电站10 kV母线PT高压侧熔断器熔断事故频发。经供电公司工作人员检查,初步认定是谐波谐振产生过电压导致。检修人员通过修改变电站内故障录波器启动条件,即当母线PT高压保险熔断后,母线电压无法采集,将无压信号传递至故障录波器启动故障录波功能,记录谐振过电压出现时及之前的母线电压波形,如图9所示,其电压幅值最大达到了7.36 kV,较相电压6.06 kV放大了1.21倍。
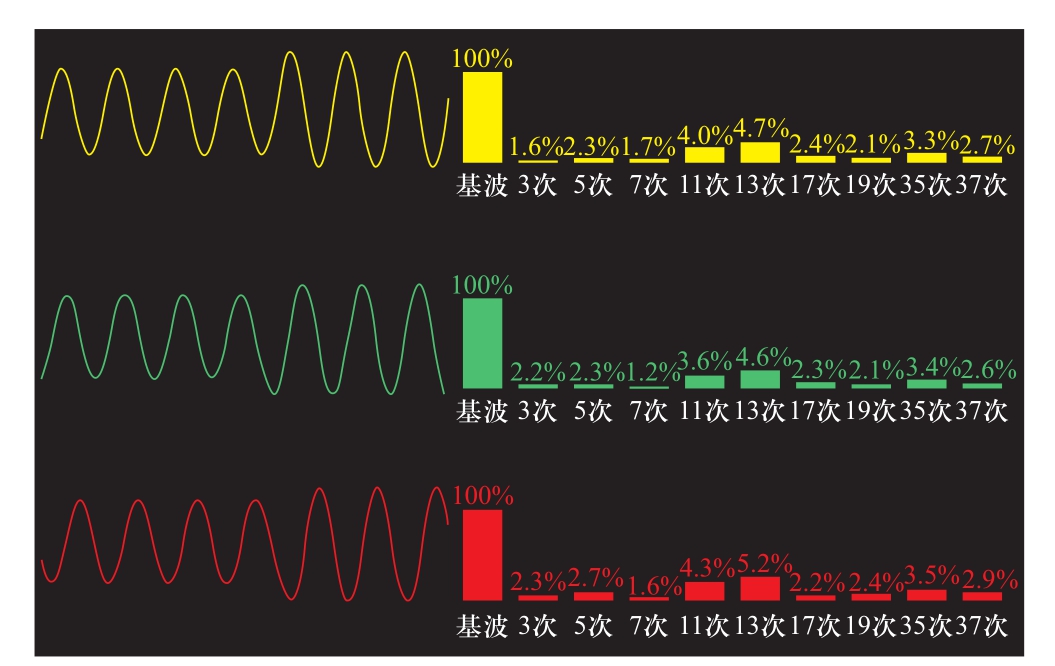
图9 变电站10 kV母线电压波形
Fig.9 Voltage waveforms of substation 10 kV bus
PWM整流型充电机采用脉动数更高的高频整流技术,具有功率因数任意控制、直流侧电压任意控制及网侧谐波含量低等优点。为找出引起系统谐振的谐波源,当电动汽车充电站没有充电机运行时,使用Fluke F1738型电能质量测试仪采集变电站10 kV母线电压数据,结果如图10所示。

图10 充电站离网时母线电压波形
Fig.10 Voltage waveforms of bus when charging station is off-grid
由图10可知,充电站未投入运行时,局部配电网的背景谐波中11次、13次和35次谐波含有率最大值分别为3.4%、3.8%和3.0%。当充电站投入运行后,配电网中11次、13次和35次谐波含有率最大值分别为4.3%、5.2%和3.5%。即电动汽车充电站投入运行后,11次、13次和35次谐波含有率分别提高了1.26倍、1.37倍和1.17倍。
综上所述,由于背景谐波的存在,电动汽车充电站在额定功率工作时,该变电站10 kV母线(节点7)处可能会发生11次和13次谐波谐振,导致母线电压升高,进而引起母线PT高压侧熔断器熔断故障,也从侧面验证了模态分析法的正确性。
4.4 元件参数灵敏度分析
4.4.1 电缆长度对配网谐波谐振影响分析
本文以关键模态5为例进行分析,改变电缆2的长度,得到不同电缆线路长度下模态分析结果如图11所示。
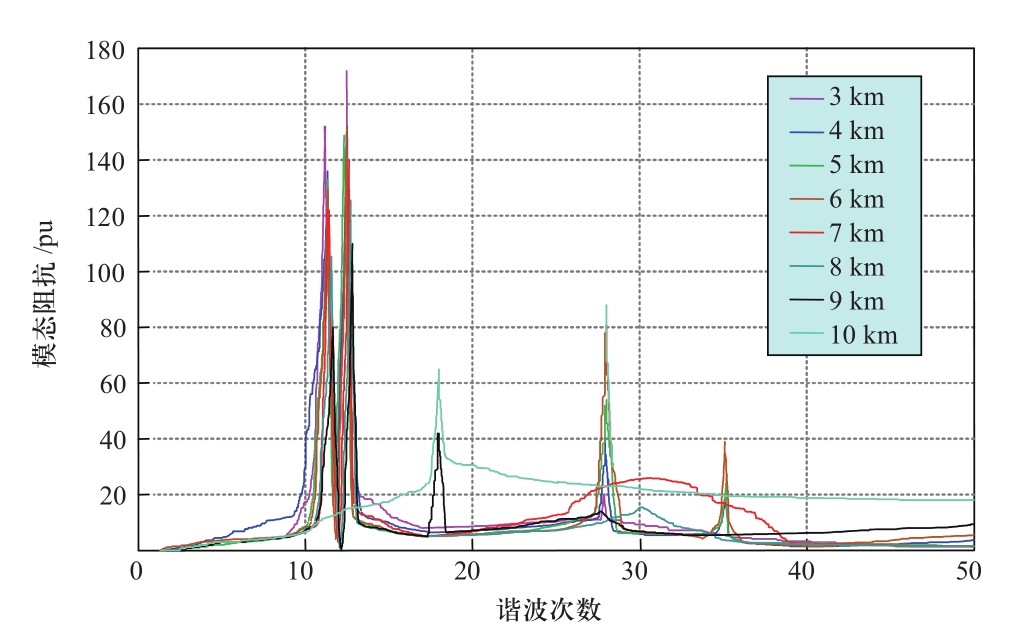
图11 不同电缆长度对应的模态分析结果
Fig.11 Modal analysis results under different cable length
由图11可看出,随着电缆长度的变化,关键模态5的谐振频率也在不断变化。当电缆长度由6 km减小到3 km时,关键模态5的谐振频率变化量较小,但模态阻抗增大了,与前文元件的归一化灵敏度分析结果一致,从侧面验证了模态分析法的正确性;当电缆长度由6 km增加到10 km时,关键模态5的谐振频率发生了较大变化,尤其是电缆长度为9 km和10 km时,模态阻抗急剧减小,11次和13次谐波依然存在,但又增加了17次谐波,其模态阻抗接近于11次谐波的模态阻抗。由此说明电缆线路的长度(亦即对地电容)对系统谐波谐振会产生较大影响。
4.4.2 充电机运行工况对配网谐波谐振影响分析
将PWM整流型充电机的直流电压输出设置为400 V时,局部配电网的模态分析结果如图12所示。
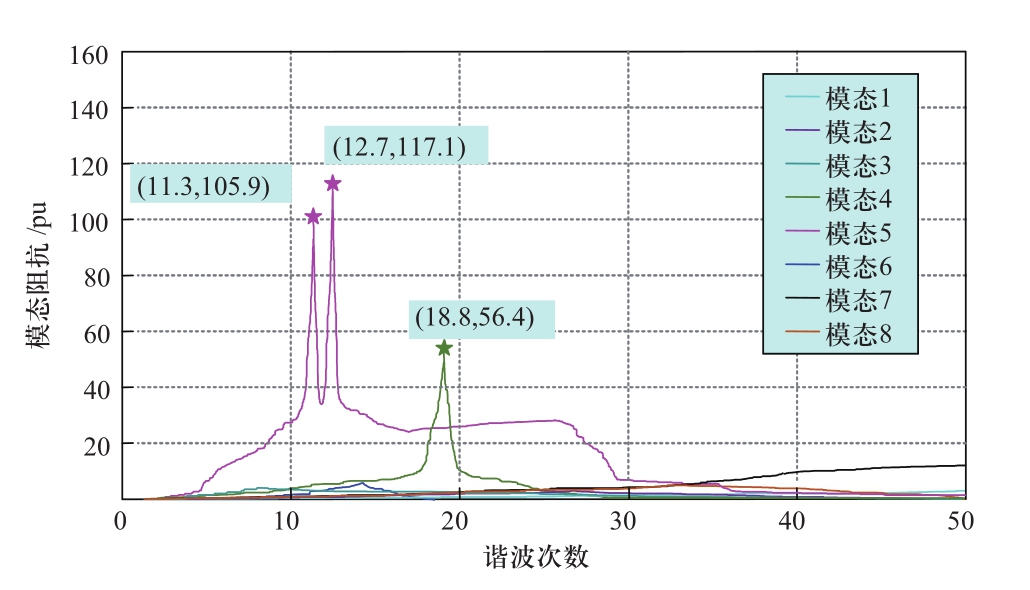
图12 直流输出电压为400 V时模态分析结果
Fig.12 Modal analysis results when DC output voltage is 400 V
由图12可知,PWM整流型充电机输出电压为400 V时,该配电网也存在11次和13次谐波,而且还增加了19次谐波,但是模态阻抗减小了很多,若采用有效的谐波抑制措施,11次、13次和19次谐波可满足国家标准谐波电压限值,不会影响配电系统的运行。
5 结论
电动汽车低碳环保,其数量将持续增长,必将促使充电站的大量建设,将对城市配电系统造成谐波污染,及时有效解决谐波污染尤其重要。本文提出了电动汽车充电站并网谐振分析方法,得出以下结论。
1)本文基于双闭环控制的PWM整流型电动汽车充电机阻抗模型,建立了多座电动汽车充电站并网谐振分析模型,该模型的谐振分析结果可为电动汽车充电站规划选址提供支撑。
2)引入节点参与因子和元件灵敏度值,推导出电缆对地分布电容和充电机输出电压是影响系统谐振的主要因素,规划运行人员应重点关注。
参考文献
[1]Kazda T, Vondrák J, Visintin A, et al.Electrochemical performance of Mo doped high voltage spinel cathode material for lithium-ion battery[J].Journal of Energy Storage, 2018, 15:329-335.
[2]周天沛,孙伟.基于充电设备利用率的电动汽车充电路径多目标优化调度[J].电力系统保护与控制,2019,47(4):115-123.
Zhou Tianpei, Sun Wei.Multi-objective optimal scheduling of electric vehicles for charging route based on utilization rate of charging device[J].Power System Protection and Control,2019, 47(4): 115-123(in Chinese).
[3]The Electric Vehicle World Sales Database.http://www.evvolumes.com.
[4]邓磊,刘敏,应丽云,等.不同充电模式下电动汽车充电站的仿真与谐波分析[J].电力系统保护与控制,2018,46(1):87-95.
Deng Lei, Liu Min, Ying Liyun, et al.Simulation and harmonic analysis of electric vehicle charging station under different charging modes[J].Power System Protection and Control,2018, 46(1): 87-95(in Chinese).
[5]汪颖,罗代军,肖先勇,等.超高次谐波问题及其研究现状与趋势[J].电网技术,2018,42(2):353-365.
Wang Ying, Luo Daijun, Xiao Xianyong, et al.Review and development tendency of research on 2-150 kHz supraharmonics[J].Power System Technology, 2018, 42(2):353-365(in Chinese).
[6]晏小彬,刘天琪,李兴源,等.送端多直流落点谐波耦合引发铁心饱和不稳定的研究[J].电力系统保护与控制,2012,40(16):1-7, 14.
Yan Xiaobin, Liu Tianqi, Li Xingyuan, et al.Research on core saturation instability caused by harmonic coupling in multiinfeed HVDC on the sending end[J].Power System Protection and Control, 2012, 40(16): 1-7, 14(in Chinese).
[7]杨文荣,刘剑飞,王胜恩,等.频率扫描法在线测量配电网脱谐度[J].仪器仪表学报,2001,22(S1):92-93.
Yang Wenrong, Liu Jianfei, Wang Sheng'en, et al.New method of off tuning degree measurement through scanning frequency in the distribution network[J].Chinese Journal of Scientific Instrument, 2001, 22(S1): 92-93(in Chinese).
[8]徐文远,张大海.基于模态分析的谐波谐振评估方法[J].中国电机工程学报,2005,25(22):89-93.
Wilsun Xu, Zhang Dahai.A modal analysis method for harmonic resonance assessment[J].Proceedings of the CSEE,2005, 25(22): 89-93(in Chinese).
[9]周辉,吴耀武,娄素华,等.基于模态分析和虚拟支路法的串联谐波谐振分析[J].中国电机工程学报,2007,27(28):84-89.
Zhou Hui, Wu Yaowu, Lou Suhua, et al.Series resonance analysis based on modal analysis and dummy branch method[J].Proceedings of the CSEE, 2007, 27(28): 84-89(in Chinese).
[10]Huang Z Y, Cui Y, Xu W.Application of modal sensitivity for power system harmonic resonance analysis[J].IEEE Transactions on Power Systems, 2007, 22(1): 222-231.
[11]唐振东,杨洪耕.基于模态分析的风电场并网谐波谐振研究[J].电力自动化设备,2017,37(3):87-92, 99.
Tang Zhendong, Yang Honggeng.Harmonic resonance research based on modal analysis for grid-connected wind farms[J].Electric Power Automation Equipment, 2017, 37(3):87-92, 99(in Chinese).
[12]唐振东,杨洪耕.偏远地区风电场并网系统串联谐振分析[J].电力系统自动化,2016,40(15):120-125.
Tang Zhendong, Yang Honggeng.Series resonance analysis on grid-connected system of wind farm in remote areas[J].Automation of Electric Power Systems, 2016, 40(15): 120-125(in Chinese).
[13]金祖洋,杨洪耕,潘爱强.多直流馈入城市输电网谐波放大特性分析[J].电网技术,2016,40(12):3857-3864.
Jin Zuyang, Yang Honggeng, Pan Aiqiang.Analysis on harmonic amplification characteristics of urban transmission network with multi-infeed DC system[J].Power System Technology, 2016, 40(12): 3857-3864(in Chinese).
[14]李晶,姜久春,牛利勇.电动汽车充电机输入阻抗特性分析[J].北京交通大学学报,2013,37(2):79-84.
Li Jing, Jiang Jiuchun, Niu Liyong.Analysis of electric vehicle charger input impedance[J].Journal of Beijing Jiaotong University, 2013, 37(2): 79-84(in Chinese).
[15]宋平岗,朱维昌,戈旺.基于微分平坦理论的单相PWM整流器直接功率控制[J].电力系统保护与控制,2017,45(5):38-44.
Song Pinggang, Zhu Weichang, Ge Wang.Differential flatness based direct power control for single-phase PWM rectifier[J].Power System Protection and Control, 2017, 45(5): 38-44(in Chinese).
[16]Xia J H, Guo Y B, Dai B J, et al.Sensor fault diagnosis and system reconfiguration approach for an electric traction PWM rectifier based on sliding mode observer[J].IEEE Transactions on Industry Applications, 2017, 53(5): 4768-4778.
[17]段庚勇,冯琳,李国杰.考虑集电网结构的海上风电场谐振研究[J].电力系统保护与控制,2016,44(22):1-11.
Duan Gengyong, Feng Lin, Li Guojie.Research on resonance of offshore wind farm considering electricity collection system[J].Power System Protection and Control, 2016, 44(22):1-11(in Chinese).
[18]Rahimi S, Wiechowski W, Randrup M, et al.Identification of problems when using long high voltage AC cable in transmission system II: Resonance & harmonic resonance[C]//2008 IEEE/PES Transmission and Distribution Conference and Exposition,April 21-24, 2008.Chicago, IL, USA.New York, USA: IEEE,2008.
Grid-connected Resonance of Electric Vehicle Charging Station Based on Modal Analysis
HUANG Yuhui1, ZHANG Tao2*, LIU Dong1, LI Qingsheng2
(1.School of Electrical Engineering, Shanghai Jiaotong University, Minhang District, Shanghai 200240, China;2.GuiZhou Power Grid Corporation, Guiyang 550003, Guizhou Province, China)
Abstract: A grid-connected resonance analysis model of an electric vehicle (EV) charging station is proposed based on modal analysis to solve the problem of harmonic resonance of the cable used in urban distribution networks, which causes the high voltage side fuse of the voltage transformer on a 10 kV bus of the substation to be frequently damaged.First, the input impedance model of a single charger is formulated based on the double closed-loop control method of a PWM rectifier.Next, the equivalent impedance model of the cable is formulated based on the distributed parameter model of the line.Then, the grid-connected model of an EV charging station with multiple chargers is also formulated.Harmonic resonance analysis flow of grid-connection of an EV charging station with node participation factor and element sensitivity index is performed.Finally, a real local distribution network is used as a case study,and results show that the proposed method can quickly resolve the harmonic resonance of the grid-connection of EV charging stations; furthermore, we verified that the distributed cable capacitances and DC output voltage of the charge pile obtained by calculating the normalized sensitivity value of the element significantly affect the resonance.Therefore, planners should focus on these factors during planning and designing.
Keywords: modal analysis; electric vehicle charging station;grid-connected harmonic resonance; participation factor;element sensitivity
文章编号:2096-5125 (2019) 06-0617-08
中图分类号:TM711;U491.8
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.06.012
基金项目:国家高技术研究发展计划项目(863计划)(2014AA051902);贵州电网公司科技项目(067600KK52170015)。
National High Technology Research and Development Program of China(863 Program) (2014AA051902); Science and Technology Foundation of GuiZhou Power Grid Corporation (067600KK52170015).
收稿日期:2019-07-05;修回日期:2019-08-08。
作者简介:

黄玉辉
黄玉辉(1983),男,博士,助理研究员,从事智能配电网、主动配电网、信息物理系统研究,E-mail:77213808@qq.com。
张涛(1969),男,高级工程师,从事电网运行分析、信息化技术应用研究。通信作者,E-mail:430050364@qq.com。
刘东(1969),男,教授,博士,从事智能配电网、主动配电网、信息物理系统研究。
李庆生(1971),男,高级工程师,南方电网三级技术专家,主要从事电力系统运行、分布式能源、智能电网等方面的工作。
(责任编辑 张宇)
