0 引言
以光伏为代表的新能源发电技术,正深刻改变着全球的电力与能源结构[1-2]。光伏发电的不确定性推动着储能技术的应用和发展,广域布局的光伏与分布式储能系统(distributed energy storage system,DESS)的有效结合已成为当前配电网安全、经济和高质量运行研究的热点。
含分布式光伏和DESS的配电网优化运行研究需要解决下述问题:1) 首先需要对光伏出力情况进行预测分析,快速精确的出力预测是实现优化运行的基础和前提。2) DESS在优化运行过程中会出现荷电状态(state of charge,SOC)不均衡现象,一方面,过量充放电会影响储能运行寿命;另一方面,储能剩余容量不足会影响优化效果。因此,有必要实现DESS的SOC均衡。3) 针对相应的优化目标,建立优化运行模型并采用合适的求解算法计算。
目前,光伏出力预测的主要形式分3种:点预测[3-4]、概率预测[5-6]和区间预测[7]。相较于前2种预测方式,区间预测不用将预测精度确定至某一点,并且无需得出光伏出力具体的概率分布情况,只需要考虑光伏出力的上下限值,更具有工程应用价值[8-9]。现有的光伏功率区间预测方法主要通过训练历史数据,得出整体规律,进而预测功率上下限,包括神经网络算法[10]、极限学习机[11-12]、经验模态分解[13]以及各种组合算法[14]。上述文献均是通过训练日前历史数据而形成的离线预测,缺乏相邻时段功率关联性的分析,同时缺少对各类气象数据的分类,导致预测准确度降低。本文考虑到光伏输出功率分布在各类不同天气情况的差异性,分类并选取相似日的数据作为历史数据,提出结合相邻时段实时预测误差与极限学习机(extreme learning machine,ELM)的光伏功率区间预测方法。
在DESS的SOC均衡方面,文献[15]提出改进的分布式下垂控制方案,通过变下垂系数实时调节SOC平衡速度。文献[16]将SOC信息引入储能充电方案,提出改进系统电流调节性能的电流校正策略,但未考虑放电过程中的SOC均衡。文献[17]提出一种附加cuk电路模块的方法均衡SOC,但控制复杂且增加了运行成本。上述文献从不同方面提出了SOC均衡方案,但未将SOC均衡与系统优化运行结合起来,未考虑均衡与优化的对立性,并且对于不确定的区间预测,传统的确定SOC均衡方法已不再适用。为此,将DESS的SOC均衡与系统优化相结合,对DESS的SOC按区间划分,形成离散的SOC水平,以单个储能与总体储能SOC离散量相差程度为标准设置DESS参与系统优化的出力。一方面,将DESS的SOC均衡与系统优化相结合,实现了二者兼顾;另一方面,将DESS的SOC作离散化处理,无需实时进行SOC均衡,减少了DESS通信的压力。
在建模和求解方面,本文构建了包含储能运行成本、系统网损和电压偏差的多目标区间优化运行模型。为避免区间量直接参与运算,将区间量通过仿射表示,并利用区间泰勒展开的仿射算法将不确定区间潮流问题转化为确定性代数方程组实现潮流计算。所提模型为多变量连续优化模型,为避免多次潮流计算,在无储能参与配网优化运行的潮流计算基础上,依据电压-功率和网损-功率灵敏度矩阵重新表达目标函数,并采用线性规划法求解。
1 光伏功率区间预测
光伏功率区间预测是指在一定置信度下,预测各时刻光伏功率出现的上、下界限值。光伏功率区间预测需要得出功率的上下边界,可以向决策者提供功率具体的范围参数,切实提高电力系统应对光伏出力变化的能力。结合相邻时段实时预测误差的ELM光伏功率区间预测方法步骤如下:
1)获取历史数据,按日气象类型分类,形成训练样本集![]() 和
和![]()
2)通过分类后的训练样本训练ELM模型,测试输出值;
3)重复步骤2),得出N个输出值,从而获得模型预测真实回归值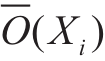 和模型误差的方差
和模型误差的方差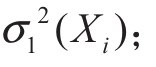
4)求出相邻时段实时预测误差的方差 并与模型误差结合形成总误差的方差
并与模型误差结合形成总误差的方差
5)根据测试数据输出预测真实回归值以及总误差,得出预测区间。
光伏电站历史数据量庞大,若直接对历史数据进行泛性学习,不仅难以得出训练结果,而且会导致预测结果不精确。为此,首先将数据按气象因素划分为晴、阴、雨,并选取相似日数据进行训练学习,有助于提高预测精度。在数据分类的基础上提出结合相邻时段实时预测误差与ELM的光伏功率区间预测方法。
1.1 极限学习机理论
ELM是一种用于训练单隐含层的前馈神经网络[12],具有训练时间短、学习效率高等优势,结构如图1所示。
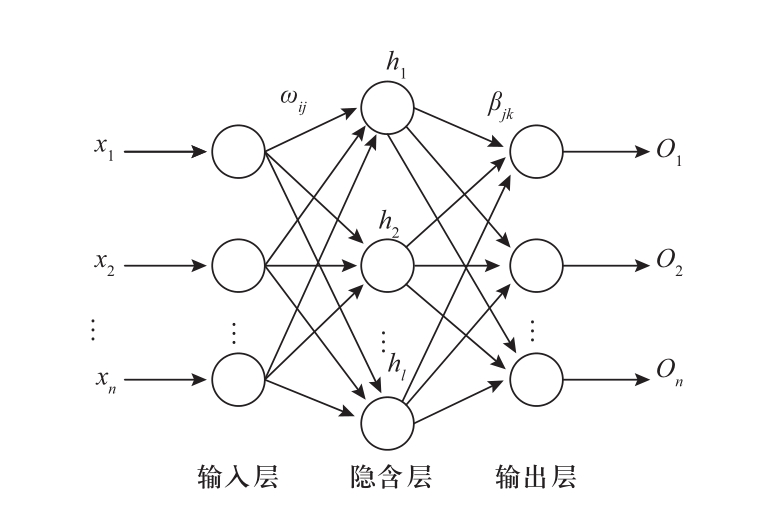
图1 ELM模型Fig.1 ELM model
给定N个训练样本(Xi, Yi),单隐含层输出可表示为:
式中:βi表示输出权重;h(x)表示激活函数;Wi·Xj表示Wi和Xj的内积;Wi表示输入权重;bi表示第i个隐含层单元的偏置量;Oj表示输出量。
ELM学习的目标是输出误差最小,即Oj与Yj差的范数最小。式(1)可转化为
式中:Y表示期望输出向量;H表示隐藏层输出矩阵;β表示连接隐藏层和输出层的输出权值。
根据Moore-Penrose广义逆矩阵理论[18],对于随机确定的Wi和bi,H被唯一确定,β为
式中:I表示对角矩阵;C表示惩罚系数;Y表示输出目标向量。
由此,建立ELM模型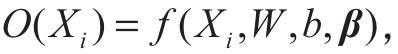 ,对于给定Xi,将预测输出平均值
,对于给定Xi,将预测输出平均值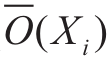 作为估计真实回归值,同时求出模型方差
作为估计真实回归值,同时求出模型方差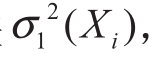 ,得:
,得:
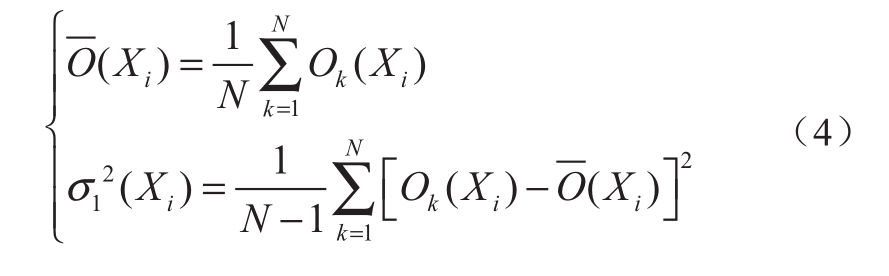
1.2 相邻时段实时预测误差
通过式(4)得出的估计回归值以及模型误差可以表征预测数据的普遍性,但对于日内实测数据的特殊性表征不够。为此,引入相邻时段实时预测误差:
式中: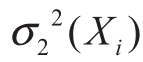 表示相邻时段实时预测误差的方差;S表示预测前的S个时间段;y(Xi,k)表示k时段光伏实际出力值;
表示相邻时段实时预测误差的方差;S表示预测前的S个时间段;y(Xi,k)表示k时段光伏实际出力值; 表示k时段ELM模型预测值。预测总误差可以表示为:
表示k时段ELM模型预测值。预测总误差可以表示为:
式中:μ为气象日类型指数。在非突变天气(晴天)下,光伏出力曲线较为平滑,近似抛物线。在突变天气(阴、雨天)下,光伏出力呈现出较为强烈的波动性和随机性。因此,对于突变天气而言,其在日内短期的功率预测误差所占比例较多,日类型指数相对较大。通过对这一地区的晴天、阴天和雨天的光伏出力进行统计计算,得出日类型指数分别为0.18、0.43和0.71。
由此,可得光伏功率预测区间:
式中,z0.9为标准高斯函数中置信度0.9所对应的临界值。
2 DESS荷电状态均衡
DESS频繁改变充、放电模式,且过量充放电会降低其循环寿命,同时,DESS的可调度量不足会影响优化效果。为此,需要研究DESS的SOC计算方法与相应的均衡策略。
2.1 DESS的SOC计算
采用文献[15]中给出的SOC估算式计算DESS中单个储能的SOC:
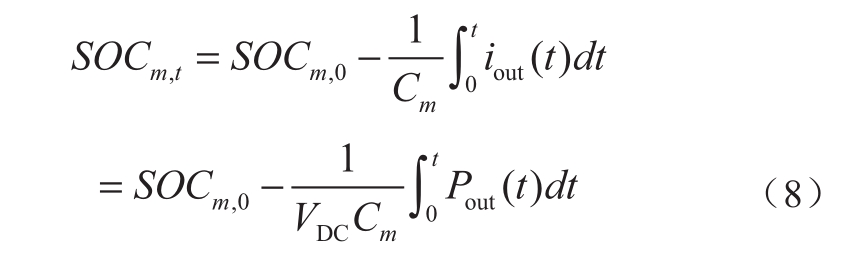
式中:SOCm,t和SOCm,0分别为t时刻和初始时刻第m个储能设备的荷电状态;iout(t)为储能设备输出电流;Cm为储能设备m的容量;iout=Pout /VDC,VDC表示储能设备输出电压;Pout(t)表示储能设备输出有功功率。可以看出,储能设备SOC状态主要由其输出的有功功率决定。
DESS的SOC平均值可表示为:
式中:SOCave,t为t时刻DESS荷电状态平均值;σm为储能设备m所占的比例系数,一般根据其容量Cm按比例设置;M为储能设备总个数。
2.2 DESS的区间离散SOC均衡
考虑到DESS的SOC均衡与优化运行的对立性,同时为减少SOC均衡的充放电次数,将DESS的SOC按区间设置离散量。经过多次仿真验证,得出离散区间为10%时,既能保证优化效果,又能较少出现SOC越限现象,故以10%设置离散区间:

式中,SOCm.表示第m个储能设备的离散SOC。
对单个储能设备m而言,若SOCm.=SOCave.,表示该储能SOC与平均值相近,输出功率根据优化最优值设置,且无需SOC均衡,反之需要根据其SOC水平,控制有功功率的合理输出,使得SOC趋于平均值,同时保证一定的优化运行效果。
设计SOC均衡影响因子,在保证DESS均衡速度的同时参与系统优化。
式中:Km表示第m个DESS的充、放电均衡影响因子;λ表示充、放电系数。利用均衡因子对储能功率进行调节,表示为
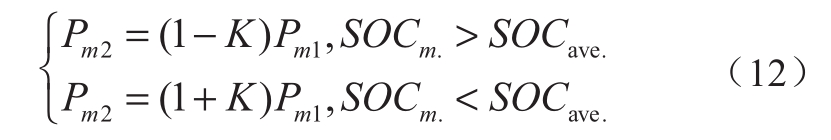
式中:Pm1表示储能设备m调节前的有功输出值,为系统最优运行状态出力值;Pm2表示通过均衡因子调节后储能设备m输出的有功功率。
2.3 DESS控制策略
依据DESS的SOC水平设置3种运行模式:
模式一:优化运行模式。若DESS的SOC处在允许范围内,并且单个储能设备的SOC离散量与平均SOC离散量相同时,通过调整其有功无功输出,实现降低网损和维持电压稳定等优化目标。
模式二:SOC均衡模式。当某一DESS的SOC水平与平均SOC相差较大时,通过区间离散SOC均衡策略控制DESS充放电功率,使整个DESS的SOC趋于均衡。
模式三:过充、过放模式。当储能的SOC状态降低至下限(5%)或者升高至上限(95%)时,为避免过度充放,DESS只在允许方向上充、放电。
DESS的运行模式只取决于平均和自身的离散SOC状态。因此,通过检测判断DESS的SOC状态,调整其运行模式,控制策略如图2所示。
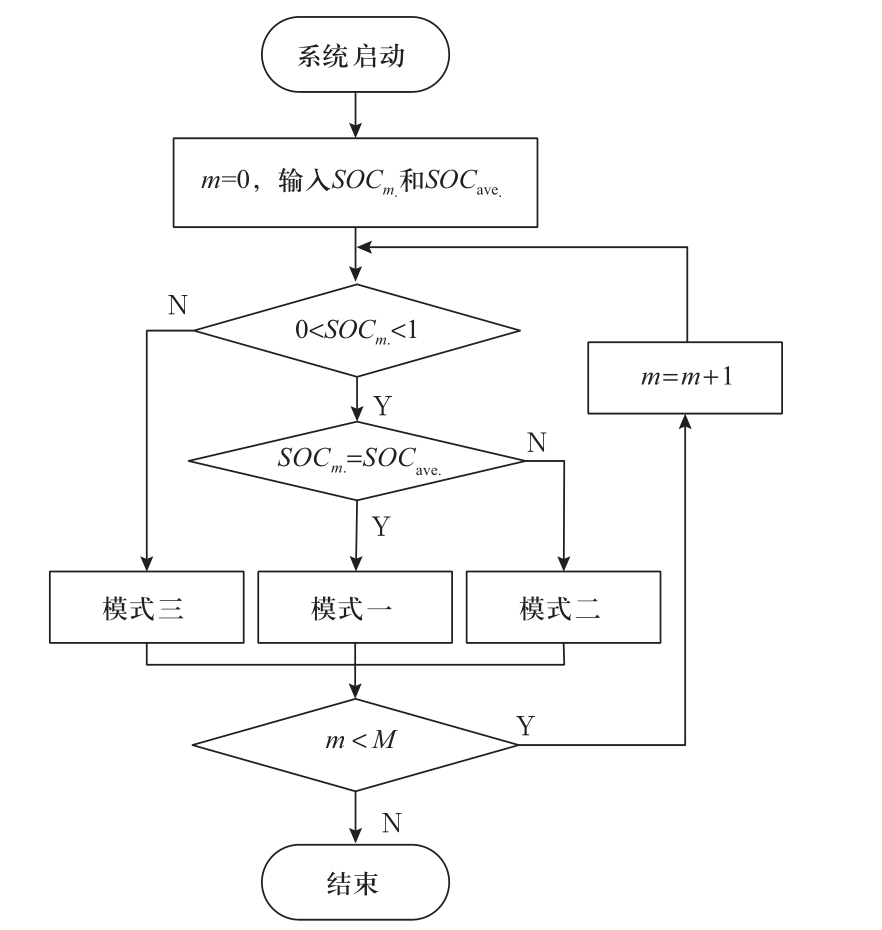
图2 DESS控制策略Fig.2 DESS control strategy
3 区间优化运行模型与求解
3.1 模型建立
3.1.1 优化目标
在对光伏功率预测的基础上,以DESS充放电功率为控制变量,以日储能运行成本最低、系统网损最小和所有节点电压偏差最小为目标,数学描述如下:
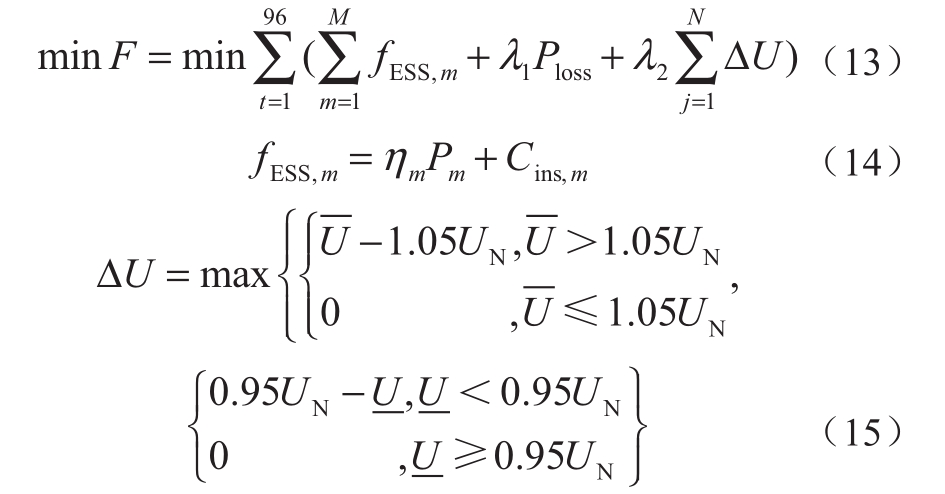
式中:fESS,m表示储能m的运行成本;Ploss表示系统网损;λ1和λ2表示平衡系数;ηm表示储能设备m运维成本;Cins,m表示储能设备m安装建设成本;ΔU表示电压越限值, 和
和 分别表示电压区间上下限;UN表示系统额定电压。
分别表示电压区间上下限;UN表示系统额定电压。
3.1.2 约束条件
1)潮流约束
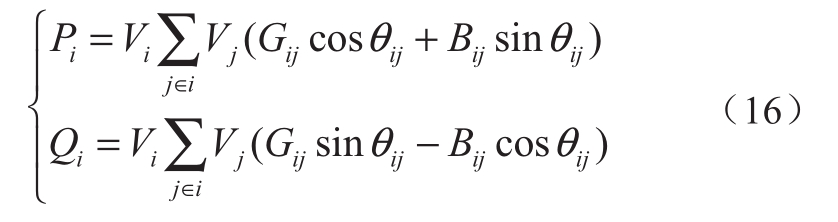
式中:Pi和Qi分别表示节点i的有功和无功功率;Vi和Vj分别为节点i和j的电压;Gij和Bij分别表示节点i和j之间的电导和电纳;cosθij和sinθij分别为相角差θij的余弦和正弦。
2)节点电压约束
式中:Ui表示节点i电压;Uimax和Uimin分别表示电压上下限。
3)储能输出功率约束
式中:Pm和Qm分别表示第m个DESS输出有功和无功;Sm表示第m个DESS对应逆变器容量。
3.2 模型求解
算法流程图如图3所示:
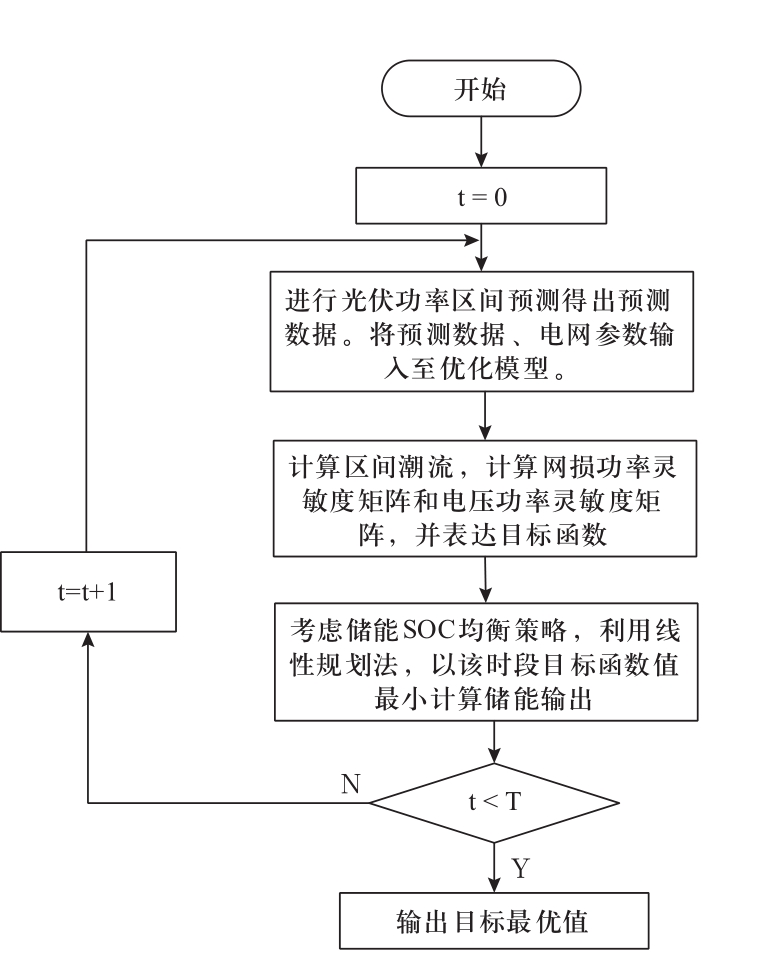
图3 算法流程图
Fig.3 Algorithm flow chart
求解算法的关键点有2处,一是对区间潮流问题的求解;二是利用灵敏度矩阵表达目标函数,并用线性规划法计算储能最优输出。
对于包含区间量的潮流方程,为避免区间迭代和保守性问题,使用基于区间泰勒展开的仿射算法[19-20]进行求解,区间量的仿射表示以及区间泰勒展开的仿射算法求解过程参见附录A。该算法避免区间量直接参与运算,克服区间算法保守性和超宽度问题;将区间潮流的求解问题转化为3个恒等式的求解,避免区间多次迭代,在提高算法收敛性能的同时大幅度减少计算量。
对于单个时段目标函数最优值的求解问题,首先由已知的网损功率灵敏度矩阵和电压功率灵敏度矩阵[21],可得ΔPloss=g1(P1,…,Pm,Q1,…Qm)以及ΔU=g2(P1,…,Pm,Q1,…Qm)的线性表达式,可将原包含储能运行成本、网损以及电压偏差的目标函数转化为求minf=f(P1,…,Pm,Q1,…Qm)的问题。目标函数及约束多为线性表示,可通过线性规划的方法求解。对于式(18)中储能输出功率容量约束等非线性约束,以验算形式判断约束成立与否,若不符合约束条件,将其等比例缩减并以确定量形式带入运算,得出目标函数及相应控制量。
4 算例分析
4.1 算例介绍
使用修改的IEEE33节点配电系统进行验证分析,系统容量10 MVA,额定电压为10 kV,线路结构如图4所示。在12、22、30处接有额定容量为600 kW的光伏电站。为考察储能对光伏并网的影响,在16、20和30节点处接入额定容量为400 kW/2 MWh的锂离子电池,能量效率为95%,循环寿命为5000次。线路参数和负荷参数参见附录A表A1和图A1。

图4 修改的IEEE33节点配电系统结构图
Fig.4 Modified IEEE33 node power distribution system structure
仿真计算机配置:处理器为intel CORE i7-7700,主频为2.8 GHz,内存为8 GB,程序编写软件为MATLAB R2014a,内置MATPOWER和CPLEX工具箱分别用于潮流计算和线性规划求解。
4.2 光伏功率区间预测分析
本文采用华东某地区一座600 kW光伏电站在某一季度的环境温度、湿度、光照直接辐射、散射辐射以及实际出力等实测数据作为参数来源。设定区间预测置信度为0.9,按照本文提出的预测方法求出的光伏功率预测区间如图5至图7所示,蓝色曲线代表预测上限,绿色曲线代表预测下限,红色曲线代表实际光伏出力值。
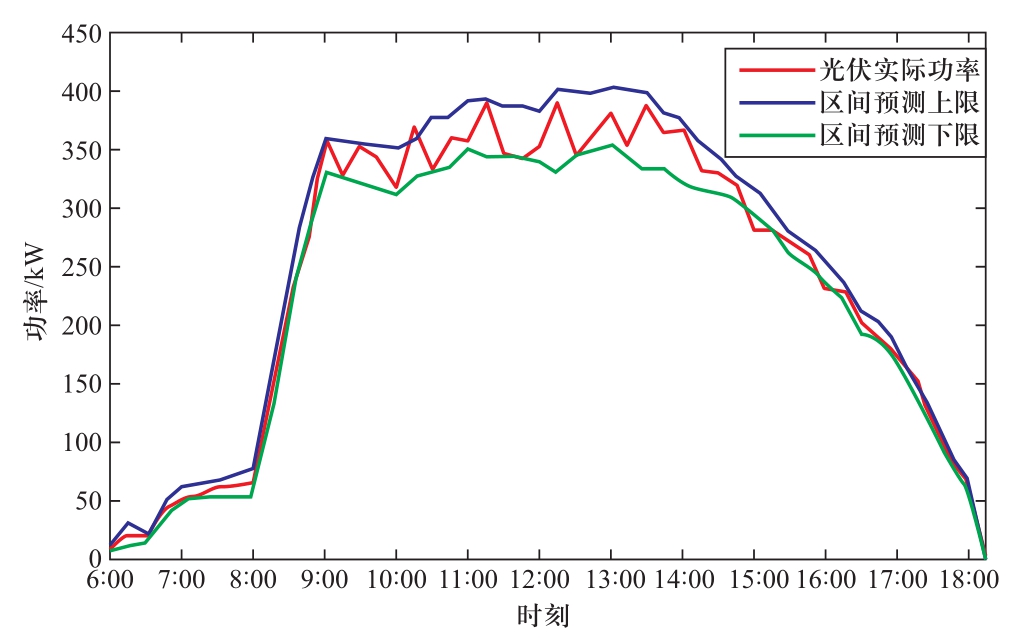
图5 晴天光伏出力预测结果
Fig.5 Sunny PV output prediction results
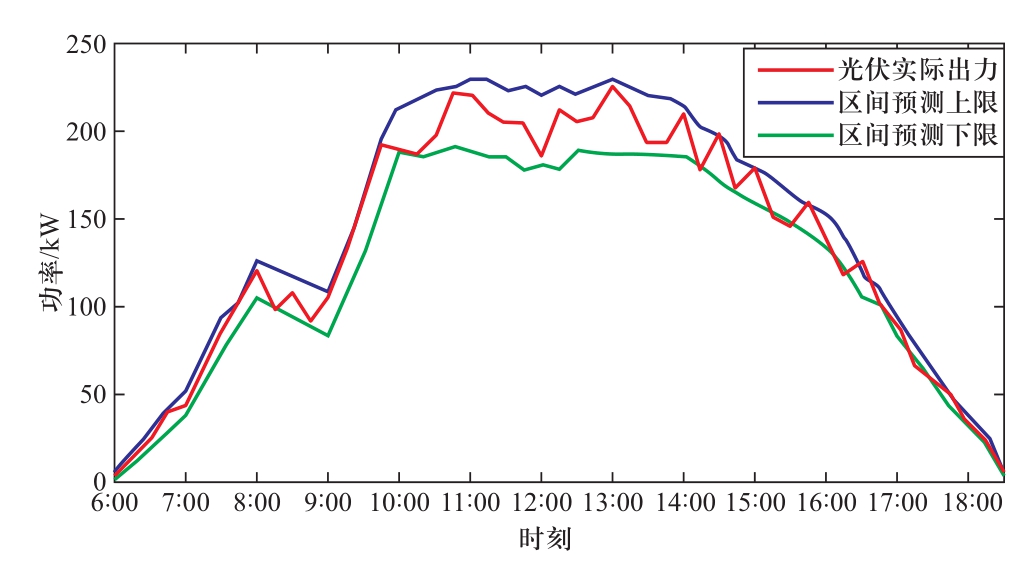
图6 阴天光伏出力预测结果
Fig.6 Cloudy PV output prediction results
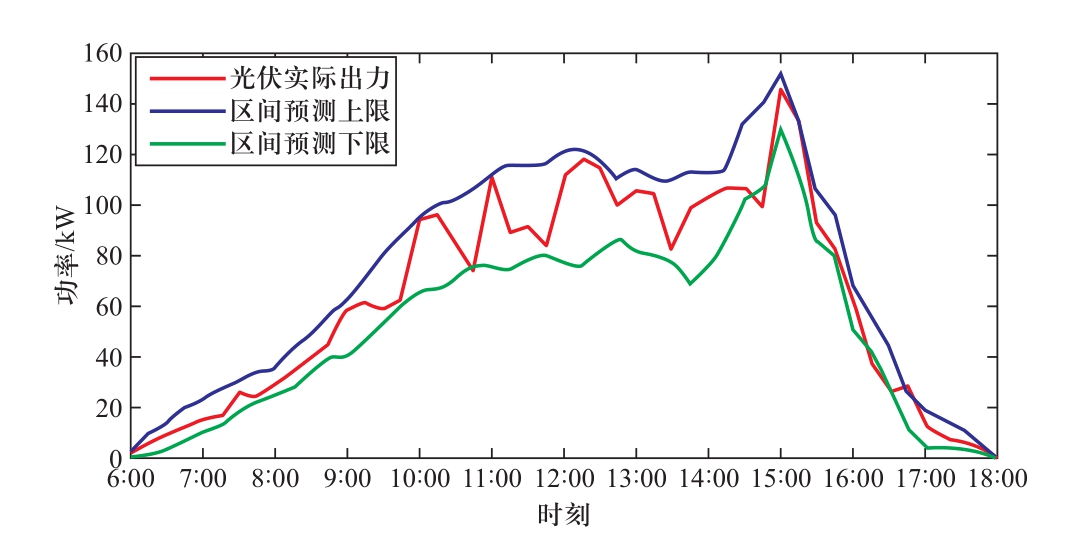
图7 雨天光伏出力预测结果
Fig.7 Rainy PV output prediction results
为评价区间估计准确性和可靠性等性能,引入区间覆盖率(prediction intervals coverage probability,PICP)和区间平均宽度(prediction intervals normalized averaged width,PINAW)等指标衡量光伏区间预测性能[8]。PICP越大说明预测区间越可靠,PINAW越小说明预测区间精确度越高。
可以看出,在不同类型气象条件下,大多数光伏实际出力值在区间预测曲线包括范围内。经计算,晴、阴和雨天PICP指标分别为92.7%、91.6%以及90.6%,PINAW指标分别为29.1 kW、27.8 kW以及23.7 kW。区间覆盖率均在置信度0.9以上,并且接近给定的置信度,同时区间宽度较小,验证了本文所提预测方案的有效性和可靠性。
为测试本文区间预测方法的性能,将其与传统ELM方法和BP神经网络方法进行对比分析。设置置信度为0.9,采用相同的训练样本和预测样本,分别计算区间预测结果,得出性能指标如表1所示。
表1 算法性能对比表
Table1 Algorithm performance comparison table
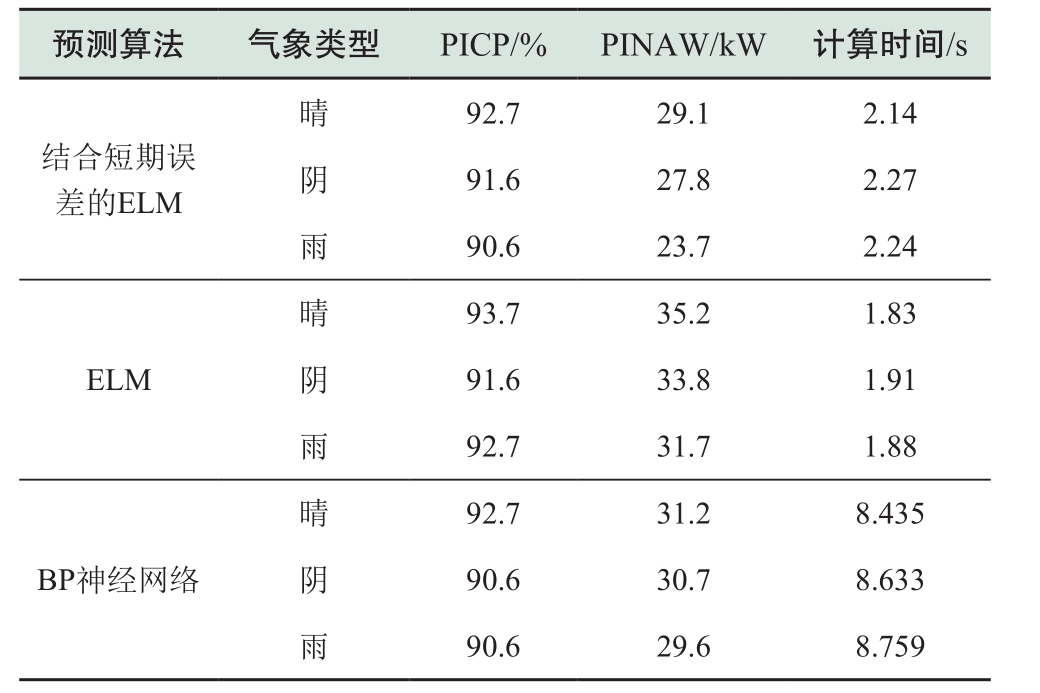
从可靠性来看,各算法PICP均保持在90%以上且相差不大,可靠性相当;从准确性来看,相对于ELM和BP神经网络方法,本文所提算法PINAW较小,相比于ELM和BP神经网络,PINAW分别减少了17%和6%以上,并且在阴雨天气下具有较高的预测精度;从计算时间来看,本文所提方法计算时间稍逊于ELM,但显著优于BP神经网络方法;分别对比各类气象条件下的算法性能,发现本文所提算法具有最强的适应性。由此可以看出,结合短期误差的ELM区间预测方法的综合性能较优。
4.3 优化运行结果分析
为验证本文所提储能离散SOC均衡策略参与配网优化运行的科学性和有效性,结合4种运行场景,对优化运行中储能越限情况、系统网损和电压状态进行分析。
场景1:无储能参与系统优化运行;
场景2:储能无附加SOC均衡措施参与优化;
场景3:储能以直接SOC均衡的方式参与优化;
场景4:储能以离散SOC均衡的控制策略实现最优运行目标。
4.3.1 储能越限情况
以全周期96个时间段内DESS的SOC达到或超过越限值次数加以说明,如表2所示。
表2 各场景DESS越限次数统计表
Table2 Statistics of DESS violation times for each scenario
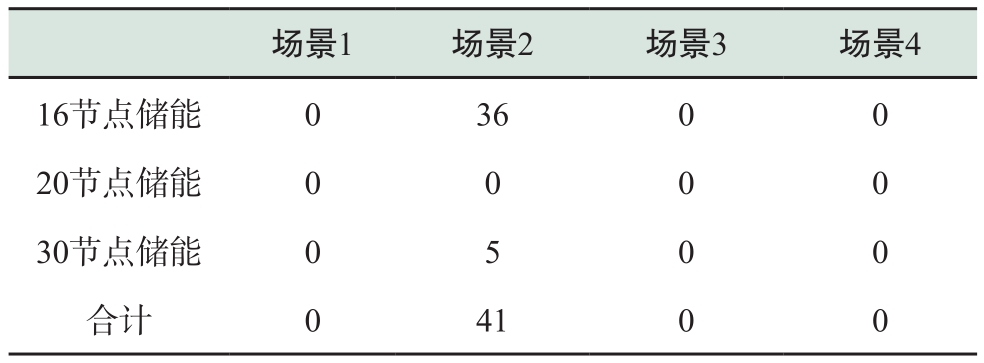
从表中可以看出,场景1储能不参与系统优化运行,故无SOC越限情况;场景3和4中储能以SOC均衡模式参与电网优化时同样无过量充放电情况;场景2中储能的SOC越限次数较多,且各储能之间差异较大。因此,DESS不附加SOC均衡措施会导致DESS的使用寿命不均,并且越限储能设备会严重影响优化效果。
4.3.2 系统网损
求解各种场景下各优化时段的系统网损,并绘制相应网损曲线,如图8所示。
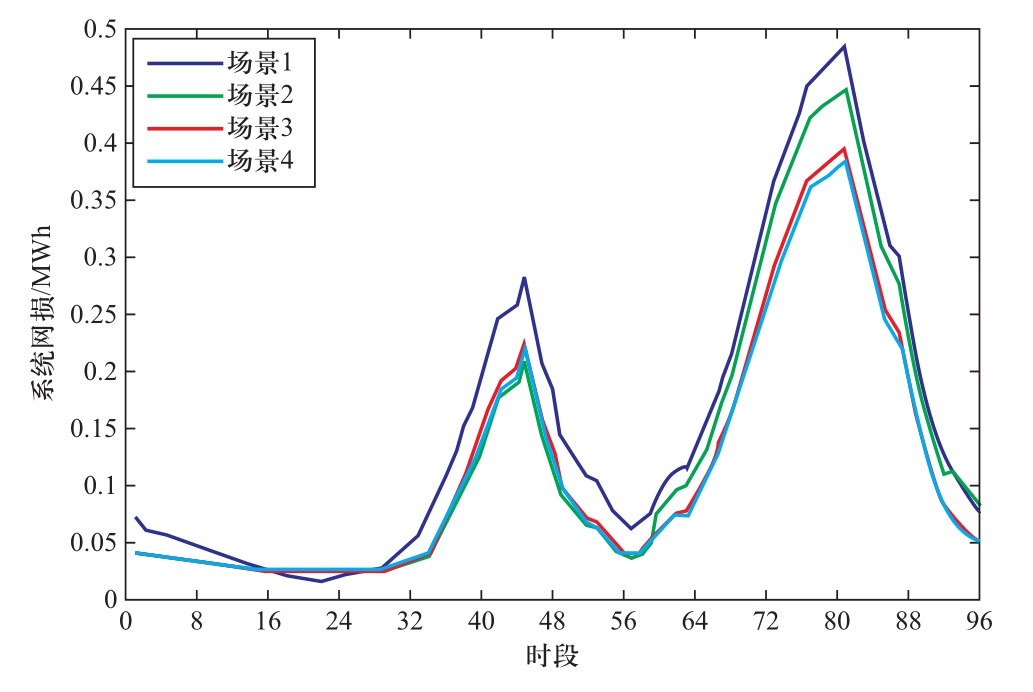
图8 各场景下系统网损曲线
Fig.8 System network loss curve in each scenario
从图8可以看出:场景1未经优化,网损最大;场景2中,前期网损最低,但从第60个时段开始,网损变大,主要是由于16节点储能设备达到最低放电深度,不能继续参与优化,在第91个时段,30节点的储能也停止优化,网损趋于未优化的场景1;场景3和4网损始终保持在较低水平,证明采用SOC均衡方法对系统网损具有更强的优化效果。在一天的前一部分时段,负荷量较少,场景2至场景4中的网损曲线基本一致;后一部分时段,负荷量大,各场景网损差异较为显著。总体网损的优化效果排序:场景4>场景3>场景2>场景1。
4.3.3 节点电压
多布点光伏接入的配电系统中,电压分布多呈现由光伏并网点和首端向馈线末端渐低的趋势。因此,光伏并网点和末端节点是衡量系统电压的重要节点。附录A中图A2给出场景1光伏并网点和末端节点电压情况。可以看出,在储能不参与系统优化运行时,节点22电压水平较高,节点33波动幅度较大,二者的电压越限现象较为严重。故以节点22和节点33为例,仿真计算出上述节点在4种不同场景下的24 h电压波动情况,如图9所示。
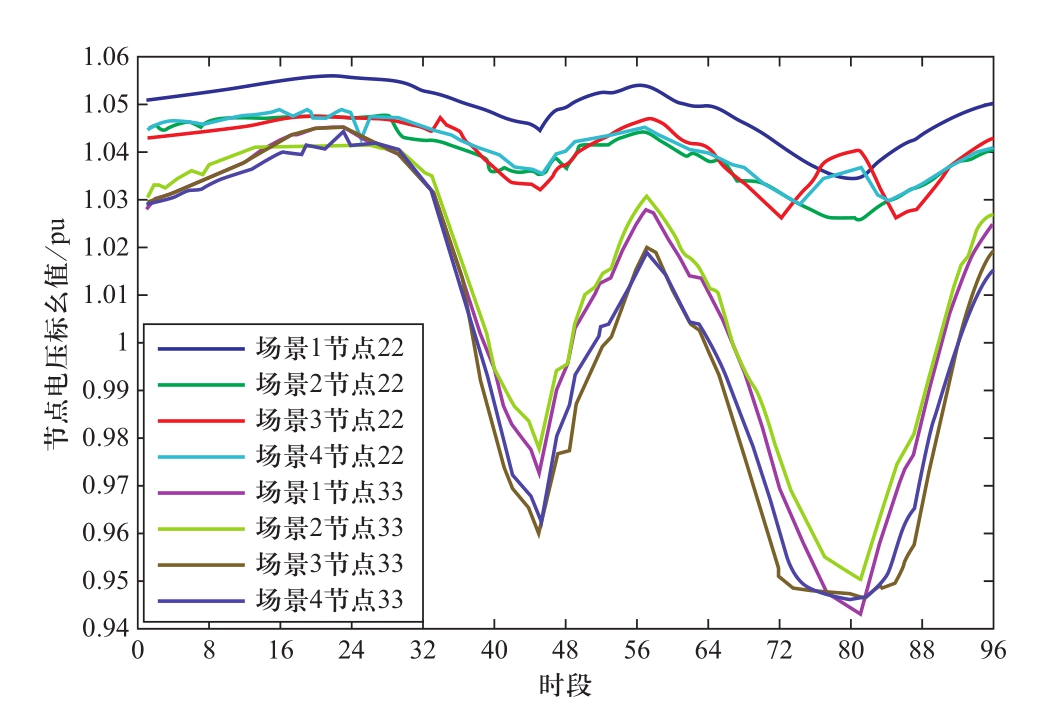
图9 各类场景下节点电压标幺值
Fig.9 Node voltage values in various scenarios
由图9可知,场景1不采用储能均衡方式运行时,电压越限情况较为严重;场景2无电压越限现象;在场景3和场景4中,24 h仿真时域内绝大部分时段节点电压标幺值在[0.95,1.05]范围内,少数越限时段为负荷高峰期,主要是由于储能容量多用于降低网损,而此时场景2中一部分储能设备运行在过充过放模式,仅能提供较多无功输出,故而无电压越限。计算得出,场景1、2、3和4中电压越限总量分别为1.78、0、0.31和0.22,说明场景4所提储能控制策略具有较强的电压调控能力,满足配网优化运行的电压要求。
综上所述,基于修改的IEEE33节点的优化结果表明:场景4的离散SOC均衡方法可以将储能过量充放电的几率降到最低,显著提升储能的运行寿命;有效降低网损,改善系统运行经济性;能够调节节点电压分布,保证系统安全高质量运行。相比于前3种运行场景,场景4中的离散SOC均衡方法具有最佳的综合优化效果。
5 结论
针对高渗透率光伏并网引起的电压问题,本文提出了计及光伏区间预测和储能SOC均衡的配电网优化方法,通过算例仿真验证了所提方法的有效性,主要结论如下:
1)提出一种结合相邻时段实时预测误差与极限学习机的光伏功率区间预测方法,在保证计算时长的情况下显著减少区间预测宽度,显著提高了预测精度;
2)提出DESS区间离散SOC均衡方案,将DESS的SOC均衡与系统优化相结合,有效降低网损和改善电压分布,同时提升了储能运行寿命,实现了配网的最优运行。
优化方法可以对未来大规模波动性可再生能源并网以及区间不确定性系统的稳态安全分析和优化运行研究提供一定的参考价值。后续研究将结合多类型分布式电源和柔性负荷的区间预测技术,同时考虑分布式电源的无功调节能力,制定更为精细化的区间预测和优化运行模型。
附录A
1)区间量转化为仿射量:
定义区间数:
式中,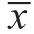 、
、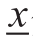 分别表示区间数x的上、下限。转化为仿射量xˆ:
分别表示区间数x的上、下限。转化为仿射量xˆ:
式中:x0和xr分别表示区间中点和区间半径;ε为噪声元,其取值在区间[-1,1]中。
2)区间泰勒展开的仿射算法:
首先将光伏出力预测区间转化为仿射形式,得出节点i的注入功率仿射量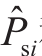 和
和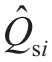 :
:
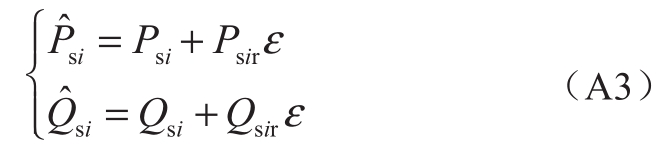
式中:Psi、Qsi、Psir和Qsir分别表示节点i注入的有功和无功仿射量中点和半径;ε为噪声元。
令线路导纳Yij= Gij + jBij,节点功率方程为:
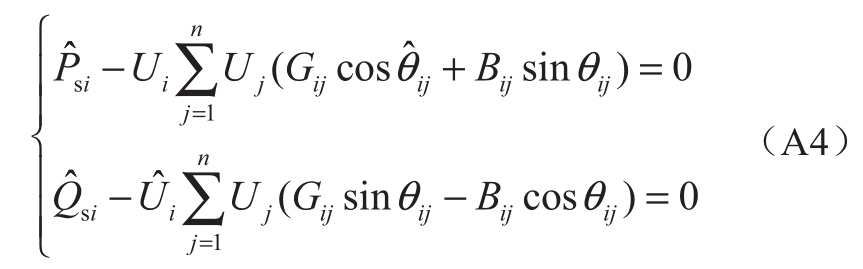
式中: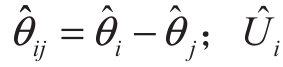 和
和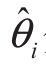 分别表示节点i的电压和相角仿射量。
分别表示节点i的电压和相角仿射量。
矩阵形式简写为
式中: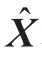 表示待求状态量的仿射向量;
表示待求状态量的仿射向量;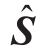 表示节点注入功率仿射向量;
表示节点注入功率仿射向量;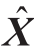 受
受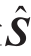 控制,
控制, 可看作
可看作 构成的隐函数
构成的隐函数 具体表示为:
具体表示为:
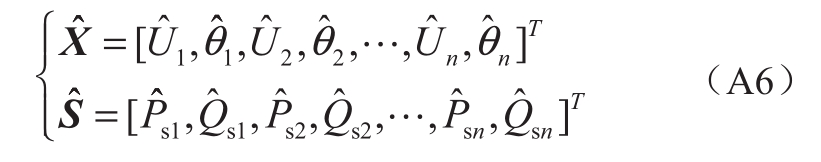
以区间变量中点为基点,将仿射式进行2阶泰勒展开,得到系统待求状态量的仿射算子展开式:
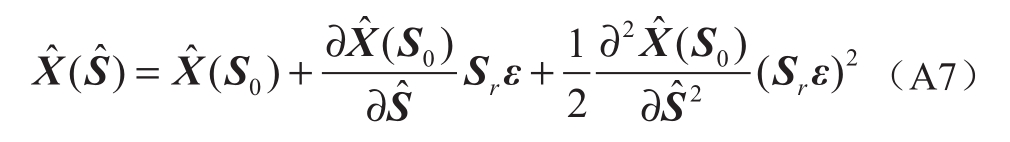
将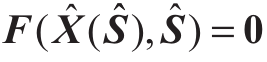 在S0处进行2阶泰勒展开可得3项恒等式,由于等式恒成立,分别令其为0,可解出
在S0处进行2阶泰勒展开可得3项恒等式,由于等式恒成立,分别令其为0,可解出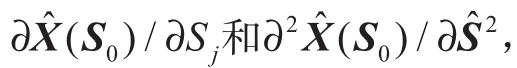 ,带入式(A7)可实现潮流方程求解。
,带入式(A7)可实现潮流方程求解。
表A1 IEEE33节点配电网系统参数数据
TableA1 IEEE33 node distribution network system parameter data
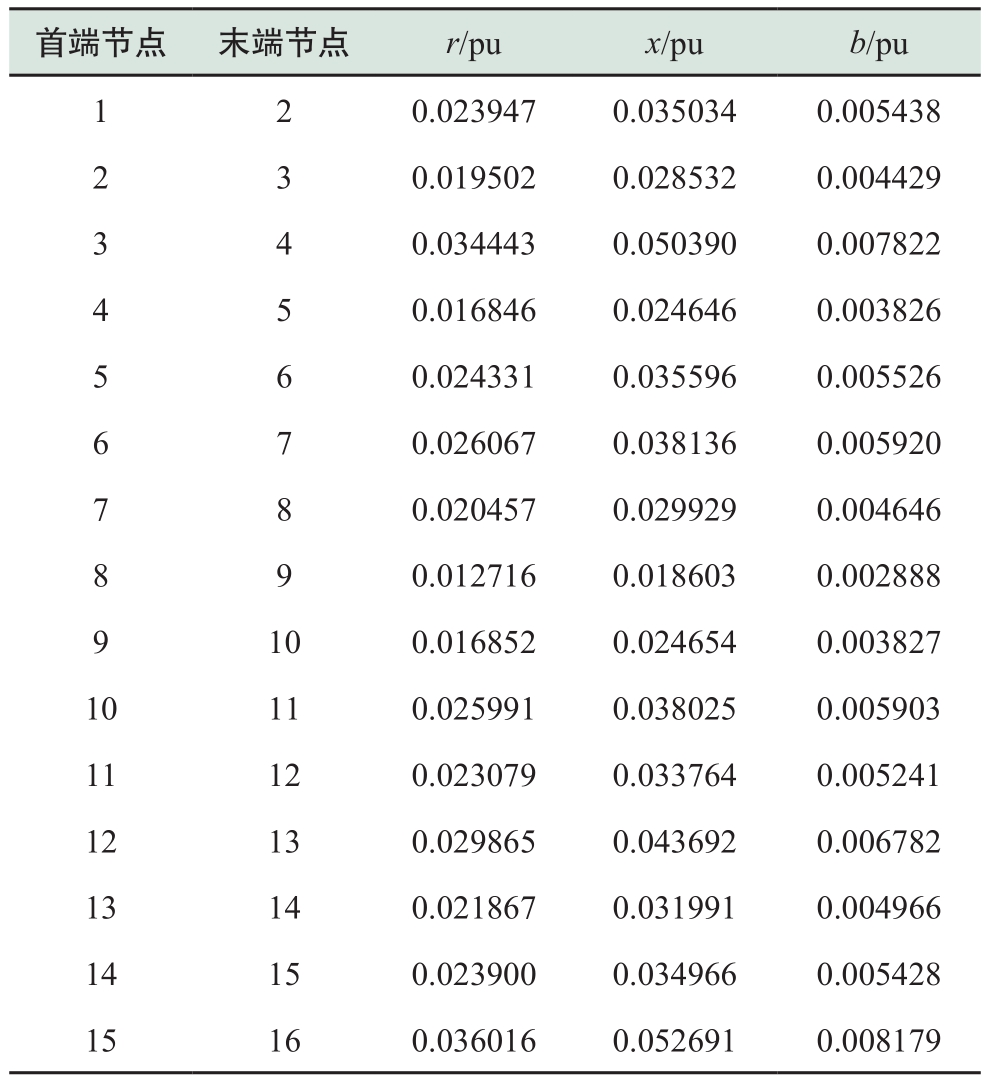
续表
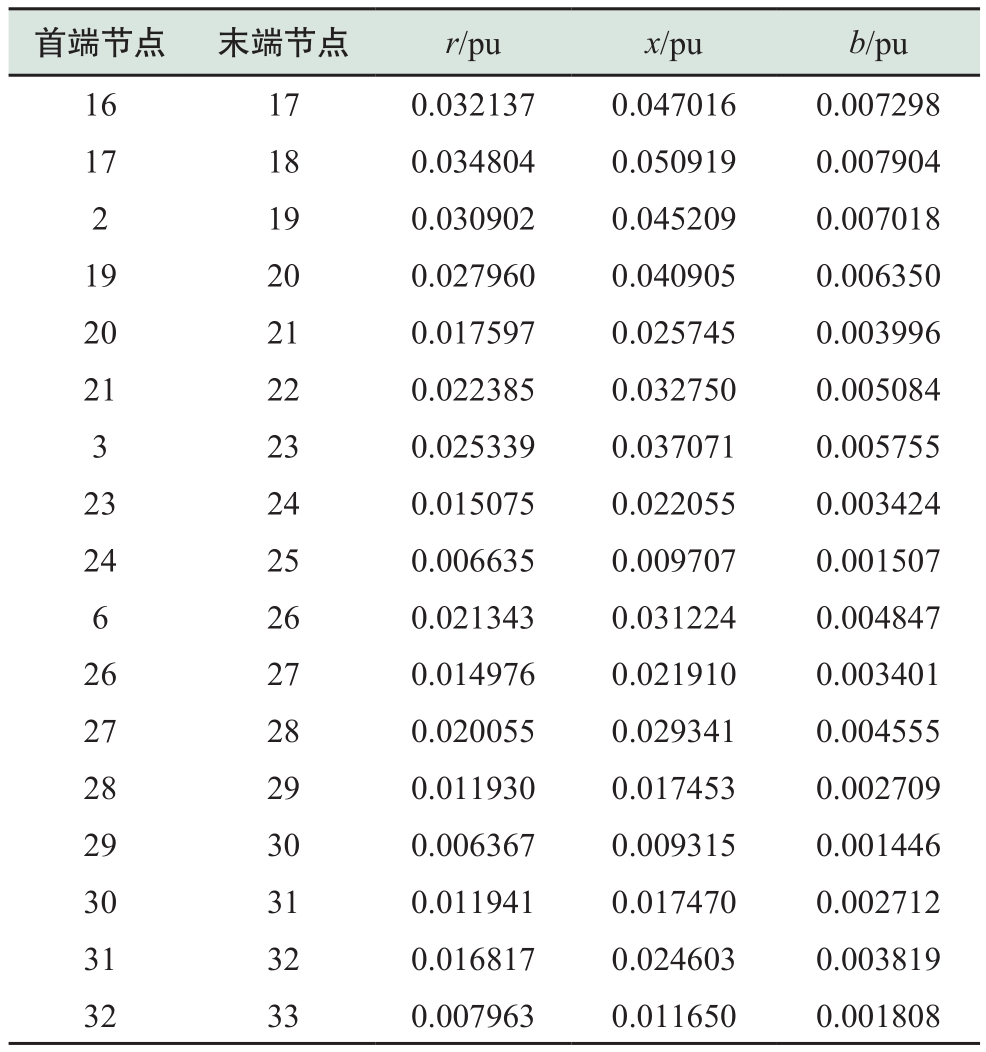
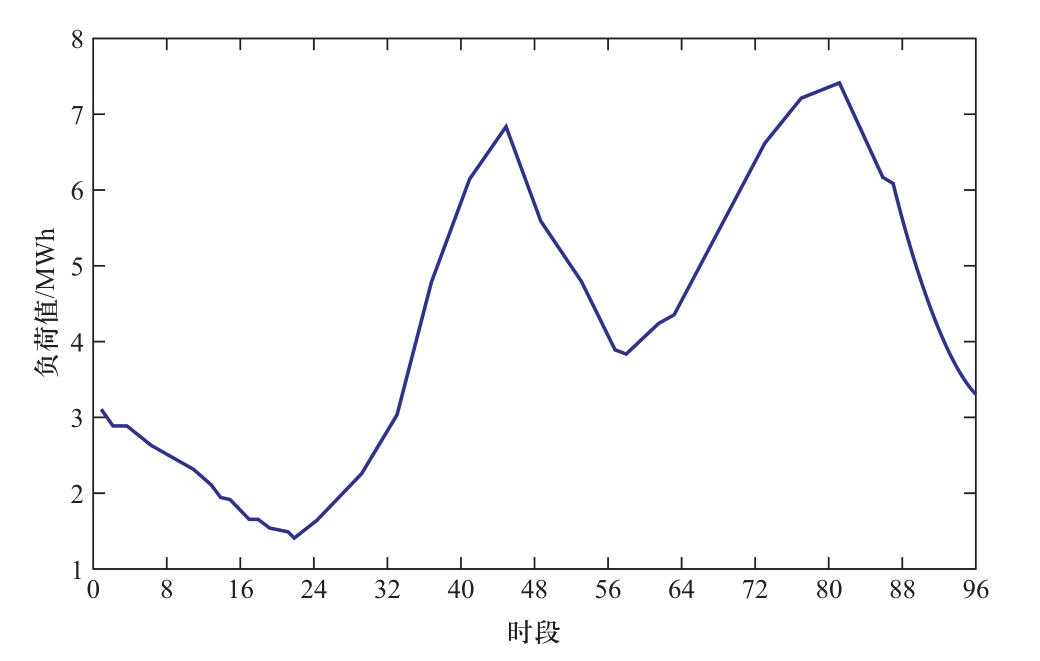
图A1 负荷曲线Fig.A1 Load curve
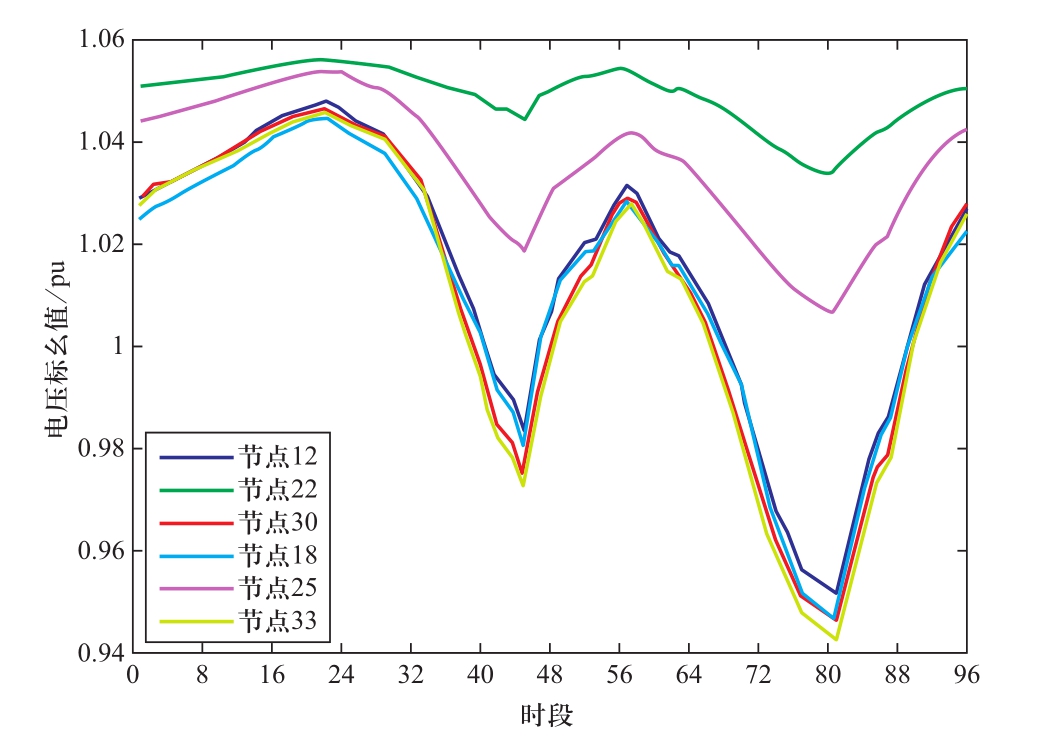
图A2 场景1节点电压曲线
Fig.A2 Scenario 1 node voltage curve
参考文献
[1]张立波,高骞,周勤勇,等.考虑可再生能源出力概率模型和预测负荷区间模型的输电网规划方法[J].全球能源互联网,2019(1):62-69.
Zhang Libo, Gao Qian, Zhou Qinyong, et al.Transmission network expansion planning considering probabilistic model of renewable power and interval model of predicted load[J].Journal of Global Energy Interconnection, 2019(1): 62-69(in Chinese).
[2]周孝信,陈树勇,鲁宗相,等.能源转型中我国新一代电力系统的技术特征[J].中国电机工程学报,2018,38(7):1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al.Technology features of the new generation power system in China[J].Proceedings of the CSEE, 2018, 38(7): 1893-1904,2205(in Chinese).
[3]Xiang Z, Ji W, Hai Z, et al.Very short-term prediction model for photovoltaic power based on improving the total sky cloud image recognition[J].The Journal of Engineering, 2017,2017(13): 1947-1952.
[4]Jang H S, Bae K Y, Park H S, et al.Solar power prediction based on satellite images and support vector machine[J].IEEE Transactions on Sustainable Energy, 2016, 7(3): 1255-1263.
[5]Li Fen, Li Chunyang, Yang Yong, et al.Short-term photovoltaic power probability forecasting based on OLPPGPR and modified clearness index[J].The Journal of Engineering, 2017, 13(1): 1625-1628.
[6]王继东,冉冉,宋智林.基于改进深度受限玻尔兹曼机算法的光伏发电短期功率概率预测[J].电力自动化设备,2018,38(5):43-49.
Wang Jidong, Ran Ran, Song Zhilin.Probability forecast of short-term photovoltaic power generation based on improved depth restricted Boltzmann machine algorithm[J].Electric Power Automation Equipment, 2018, 38(5): 43-49(in Chinese).
[7]Ying Y Q, Wu Y J, Su Y Q, et al.Dispatching approach for active distribution network considering PV generation reliability and load predicting interval[J].The Journal of Engineering, 2017, 2017(13): 2433-2437.
[8]赖昌伟,黎静华,陈博,等.光伏发电出力预测技术研究综述[J].电工技术学报,2019,34(6):1201-1217.
Lai Changwei, Li Jinghua, Chen Bo, et al.Review of photovoltaic power output prediction technology[J].Transactions of China Electrotechnical Society, 2019, 34(6):1201-1217(in Chinese).
[9]Valencia F, Collado J, Saez D, et al.Robust energy management system for a microgrid based on a fuzzy prediction interval model[J].IEEE Transactions on Smart Grid,2016, 7(3): 1486-1494.
[10]徐俊俊,吴在军,周力,等.考虑分布式电源不确定性的配电网鲁棒动态重构[J].中国电机工程学报,2018,38(16):4715-4725,4976.
Xu Junjun, Wu Zaijun, Zhou Li, et al.Robust dynamic reconfiguration for distribution networks considering uncertainty of distributed generations[J].Proceedings of the CSEE, 2018, 38(16): 4715-4725, 4976(in Chinese).
[11]Wan C, Lin J, Song Y H, et al.Probabilistic forecasting of photovoltaic generation: an efficient statistical approach[J].IEEE Transactions on Power Systems, 2017, 32(3): 2471-2472.
[12]Jing B, Qian Z, Pei Y, et al.Ultra short-term PV power forecasting based on ELM segmentation model[J].The Journal of Engineering, 2017, 2017(13): 2564-2568.
[13]陈云龙,殷豪,孟安波,等.基于模糊信息粒化的光伏出力区间预测[J].电测与仪表,2018,55(14):63-68.
Chen Yunlong, Yin Hao, Meng Anbo, et al.PV power interval prediction based on fuzzy information granulation[J].Electrical Measurement & Instrumentation, 2018, 55(14): 63-68(in Chinese).
[14]黎敏,林湘宁,张哲原,等.超短期光伏出力区间预测算法及其应用[J].电力系统自动化,2019,43(3):10-18.
Li Min, Lin Xiangning, Zhang Zheyuan, et al.Interval prediction algorithm for ultra-short-term photovoltaic output and its application[J].Automation of Electric Power Systems,2019, 43(3): 10-18(in Chinese).
[15]吴青峰,孙孝峰,王雅楠,等.基于分布式下垂控制的微电网分布式储能系统SOC平衡策略[J].电工技术学报,2018,33(6):1247-1256.
Wu Qingfeng, Sun Xiaofeng, Wang Yanan, et al.A distributed control strategy for SOC balancing of distributed energy storage systems in microgrid[J].Transactions of China Electrotechnical Society, 2018, 33(6): 1247-1256(in Chinese).
[16]Bi K T, Sun L, An Q T, et al.Active SOC balancing control strategy for modular multilevel super capacitor energy storage system[J].IEEE Transactions on Power Electronics, 2019,34(5): 4981-4992.
[17]黄剑龙,孙晓艳,刘全胜.基于SOC的储能电池组均衡策略研究[J].可再生能源,2017,35(12):1828-1834.
Huang Jianlong, Sun Xiaoyan, Liu Quansheng.Research on equalization strategy of energy storage battery strings based on SOC[J].Renewable Energy Resources, 2017, 35(12): 1828-1834(in Chinese).
[18]张宇献,郝双,钱小毅.基于误差分解和Bootstrap方法的风电功率区间预测[J/OL].电网技术:1-7[2019-04-25].https://doi.org/10.13335/j.1000-3673.pst.2018.3023.
Zhang Yuxian, Hao Shuang, Qian Xiaoyi.Wind power power interval prediction based on error decomposition and Bootstrap method [J/OL].Power System Technology: 1-7 [2019-04-25].https://doi.org/10.13335/j.1000-3673.pst.2018.3023(in Chinese).
[19]Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al.Interval method for uncertain power flow analysis based on Taylor inclusion function[J].IET Generation, Transmission &Distribution, 2017, 11(5): 1270-1278.
[20]彭寒梅,昌玲,郭颖聪,等.主从控制微电网的动态区间潮流计算[J].电网技术,2018,42(1):195-203.
Peng Hanmei, Chang Ling, Guo Yingcong, et al.Dynamic interval power flow calculation of microgrid under masterslave control[J].Power System Technology, 2018, 42(1): 195-203(in Chinese).
[21]袁爽,戴朝华,赵传,等.多异质能源接入下的无功电压局部/全局融合优化[J].中国电机工程学报,2018,38(4):1006-1015,1277.
Yuan Shuang, Dai Chaohua, Zhao Chuan, et al.Local/global collaborative optimization of reactive power/voltage with multiple heterogeneous energy sources integration[J].Proceedings of the CSEE, 2018, 38(4): 1006-1015, 1277(in Chinese).
Optimization Operation of Distribution Network Considering Photovoltaic Interval Prediction and Energy Storage SOC Equilibrium
YUAN Xiaodong1*, YU Zhenggang2, ZHANG Chenyu1, FU Xiangyun2, LI Jianlin3
(1.State Grid Jiangsu Electric Power Company Research Institute, Nanjing 211103, Jiangsu Province, China;2.Lianyungang Power Supply Company, State Grid Jiangsu Electric Power Company, Nanjing 222004, Jiangsu Province, China;3.China Electric Power Research Institute, Haidian District, Beijing 100192, China)
Abstract: Large-scale connection of photovoltaic power generation to the distribution network poses challenges to the safety and economic operation of the power grid owing to its random and intermittent characteristics.Energy storage is an effective method for solving the high-permeability photovoltaic output power fluctuations.In this study, a photovoltaic power interval prediction method combining error feedback and extreme learning machine is proposed.Furthermore, an interval discrete state of charge equalization control strategy for distributed energy storage is proposed.A multi-objective interval optimization operation model is constructed, including the energy storage operating costs, system network loss, and voltage deviation.The affine algorithm of interval Taylor expansion is used to transform the uncertain interval power flow problem into deterministic algebraic equations to calculate the power flow.Simultaneously, the objective function is expressed by voltage-power and network loss-power sensitivity matrix and solved using the linear programming method.Finally, a simulation is performed based on the improved IEEE 33 bus distribution network.Simulation results show that the proposed photovoltaic power interval prediction method can significantly improve the prediction accuracy, and the proposed energy storage control strategy can effectively reduce network loss and improve voltage distribution.
Keywords: photovoltaic; energy storage; interval prediction;SOC equilibrium; affine algorithm; sensitivity matrix
文章编号:2096-5125 (2019) 06-0598-10
中图分类号:TM727
文献标志码:A DOI:10.19705/j.cnki.issn2096-5125.2019.06.010
基金项目:国家电网公司总部科技项目(5210D0180006)。
Science and Technology Foundation of SGCC (5210D0180006).
收稿日期:2019-07-09;修回日期:2019-08-07。
作者简介:

袁晓冬
袁晓冬(1979),男,研究员级高工,研究方向为电能质量、新能源发电及并网、电力储能应用等。通信作者,E-mail:lannyyuan@hotmail.com,1838658@qq.com。
郁正纲(1972),男,研究员级高工,研究方向为电力系统运行与分析、状态监测、可再生能源发电并网等。
张宸宇(1989),男,高级工程师,研究方向为直流配电网、电能质量治理等。
(责任编辑 张宇)