0 引言
随着环境污染和气候变化等问题日益严重,全球能源领域正在掀起一场有史以来最深刻和最广泛的革命,传统电力系统难以适应新的能源供需格局和发展趋势,而以电力系统为核心的综合能源系统(integrated energy system, IES)将成为未来人类社会能源的主要承载形式[1]。综合能源系统耦合多种能源子系统[2],统一规划调度多种能源的产生、传输、转换、分配等过程,从而满足需求侧的多样化需求,提高能源利用效率,增强能源供应的灵活性。但相较于传统电力系统,综合能源系统规划设计和优化运行过程中面临着更多的不确定性因素,如空气源热泵、燃气轮机和蓄能式电暖器等新设备,这些不确定性因素使得电网、热网和气网的耦合程度大幅度增加,系统规划、运行工作更加复杂困难,给系统的安全稳定运行带来巨大挑战[3-4]。可靠性评估能够对系统进行风险评估,量化分析元件故障、检修等因素对系统可靠性的影响,便于在综合能源系统的规划运行过程中,快速准确地对系统可靠性进行评估,并依据评估结果采取相关措施。综合能源系统可靠性评估主要包括[5]:系统状态选取、系统状态影响计算和系统可靠性指标计算。系统状态影响是指系统在选定状态下为满足运行约束,在采取包括源出力调整、变压器档位调整、燃气系统压缩机功率调整等所有补救措施后,仍然需要削减的负荷量。因此,负荷削减是系统为保证有效运行所采取的最终措施,一种高效准确的电气热综合能源系统最优负荷削减量计算方法对系统规划、运行、调度等过程都有着极为重要的意义。
综合能源系统最优负荷削减算法是最为常用的一种负荷削减量计算方法[5],其目标函数是系统的负荷削减量最低,结合等式约束和不等式约束条件,利用优化方法求解得到系统在元件故障、检修等情况下的最小损失负荷,该算法可用于量化计算综合能源系统元件故障、分布式能源出力变化和负荷波动等各类不确定因素对供能充裕性和安全性的影响,并提出相应的提升措施[6]。
综合能源系统最优负荷削减算法的关键在于系统建模仿真和最优潮流算法(optimal power flow, OPF)两方面。系统建模仿真方面,瑞士苏黎世联邦理工学院提出了能源集线器模型[7-8],通过耦合矩阵来表示不同能源传输、分配、转换的过程特性,可用于综合能源系统的潮流计算[9]、可靠性分析[10]等领域。最优潮流算法方面,目前的研究可分为统一求解法[11]和顺序求解法[12]两类。前者是将各子系统潮流过程和能源转换过程综合起来建立最优负荷削减模型,但该模型的方程往往是非凸的,雅可比矩阵奇异,算法难以收敛,且计算结果也难以保证全局最优。文献[13]采用线性化的方法提出了基于MILP的电/气综合能源系统最优潮流计算方法,但难以进一步应用于电气热综合能源系统。顺序求解法也可称为解耦求解法[3],本文在文献[3]基于电气耦合系统的分层解耦优化模型的基础上,提出了一种面向电气热综合能源系统可靠性评估的最优负荷削减量分层解耦计算方法,在能源集线器的基础上将综合能源系统调度过程解耦为单一OPF问题,考虑各能源子系统之间的影响,可以高效准确地求解电气热综合能源系统在各种故障状态下的最优负荷削减量。
本文首先分别建立了电气热子系统的最优潮流计算模型,并分析耦合环节能源集线器的能量转换与分配特性;进一步,提出了一种电气热综合能源系统最优负荷削减的分层解耦算法,并给出了其应用于综合能源系统可靠性评估的算法框架。最后利用所提方法对综合能源系统算例进行可靠性评估,详细分析了该算例系统中电气热互补转化对可靠性的影响,并对系统进行了薄弱环节分析和相应可靠性提升分析。
1 综合能源系统最优负荷削减模型
综合能源系统是未来重要的能源供给形式[14]。本文所考虑的综合能源系统包括电/气/热三个子系统,三个子系统通过能源集线器形成耦合关系,从而进行联合优化调度运行,如图1所示。
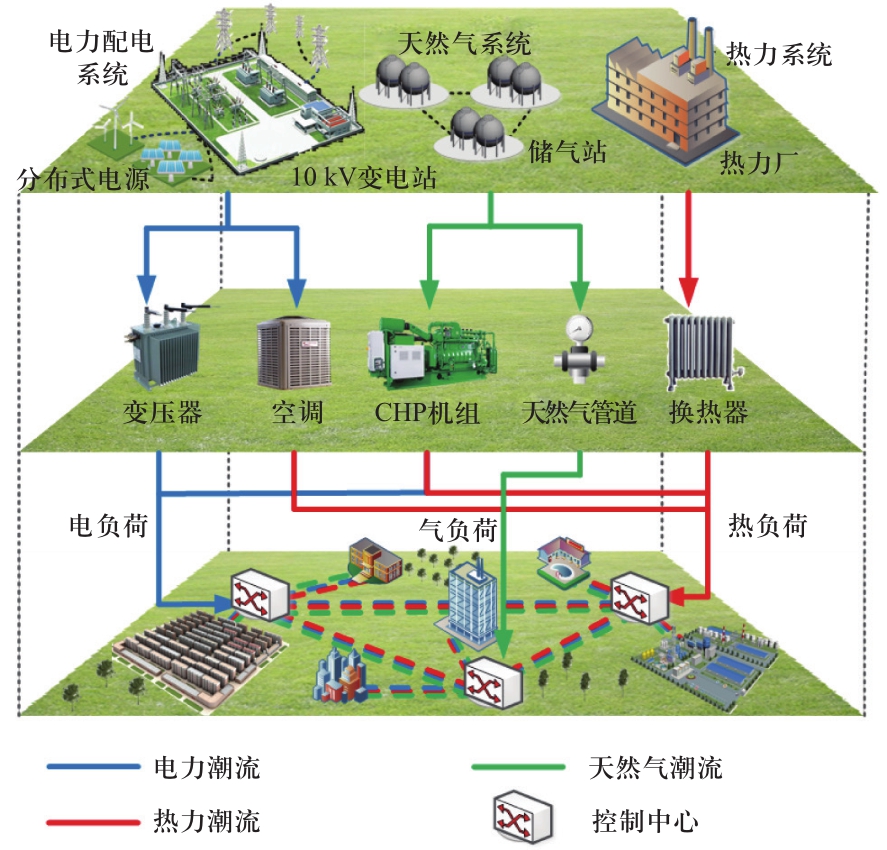
图1 综合能源系统
Fig.1 Integrated energy system
1.1 电力系统
电力系统的最优负荷削减模型以最优潮流为基础,以负荷削减量最低为目标函数:

式中:Ne为电力系统的节点数量;ΔLe,i为电力系统节点i的负荷削减量。相应模型的约束条件为:

式中:Le为电力系统节点负荷;Pe为电力系统节点潮流;P、Q、V、θ分别为电力系统的有功潮流、无功潮流、电压和相角,对应后4个公式表示其取值的上下限;fe为电网节点注入功率与节点电压关系的节点功率方程,极坐标形式下的功率平衡方程[15]为:

式中:Pi和Qi分别为节点i注入的有功功率和无功功率;Ui和Uj分别为节点i和 j的电压;Gij和Bij分别为节点导纳矩阵的电导和电纳;θij为节点i和 j电压相角差,θij= θi - θj。
1.2 天然气系统
天然气系统包括气源、输气管道、压缩机和负荷节点等。天然气由气源节点供应,通过输气管道传输到负荷节点,燃气轮机可以将天然气转化为电能和热能以供用户使用,压缩机可以提高天然气传输过程中的气压以弥补传输过程中的压力损失[16]。天然气系统的最优负荷削减模型为:
式中:Ng为天然气系统的节点数量;ΔLg,j为天然气系统节点j的负荷削减量。相应模型的约束条件为:
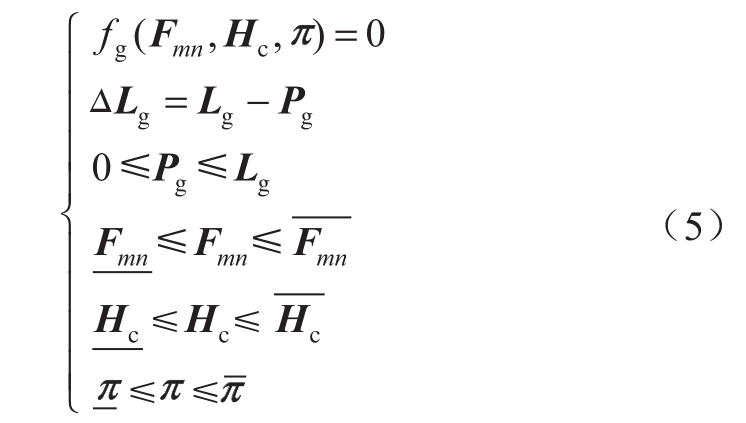
式中:Lg为天然气系统节点负荷;Pg为天然气系统节点潮流;Fmn、Hc、π分别为天然气网络支路流量、压缩机功率和节点气压,对应后3个公式表示其取值的上下限; fg为天然气系统潮流方程[17]:
式中:A为系统的拓扑矩阵,表示节点与支路的关联关系,支路包括压缩机和管道;S为气源节点出力;L为负荷节点需求;G为压缩机与节点的关联矩阵;若压缩机由燃气轮机驱动,即压缩机需要消耗一定量的天然气,Fc为压缩机消耗气体量:
式中:ac、bc和cc为拟合系数。
1.3 热力系统
热力系统的最优负荷削减模型为:
式中:Nh为天然气系统的节点数量;ΔLh,k为热力系统节点k负荷削减量。相应模型的约束条件为:
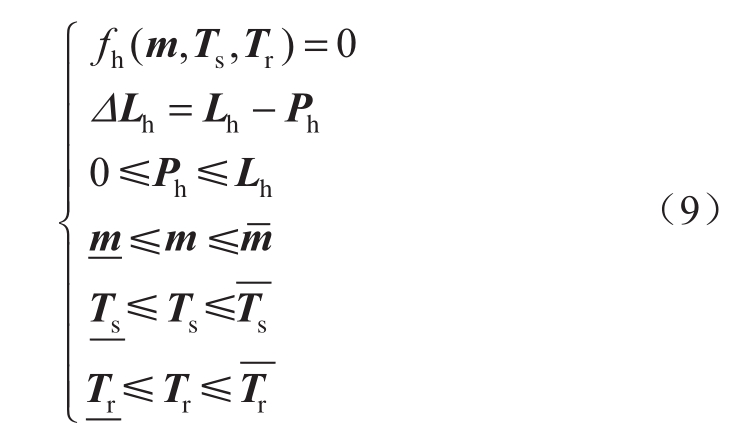
式中:Lh为热力系统节点负荷;Ph为热力系统节点潮流;m、Ts、Tr分别为管道流量、节点供给温度和返回温度,对应后三个公式表示其取值的上下限;fh为热力系统潮流方程[18]:

式中Φ为节点消耗或供给的热功率。
1.4 能源集线器
综合能源系统通过耦合元件联结电力系统、燃气系统和热力系统等,使得电/气/热各种能源之间可以相互转化、相互补充,从而提高了能源利用效率和系统能源供给的灵活性。综合能源系统中各能源子系统之间能量转化、分配和存储等过程通过多种耦合元件如热电联产机组、空调、冷热电三联供机组等设备完成,能源集线器模型[8]利用耦合矩阵准确描述综合能源系统中各种设备对电、热、气等能源的转化与分配。
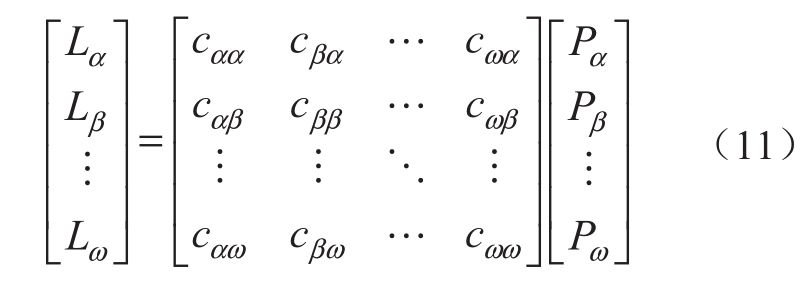
式中:L、c和P分别代表能源集线器的输入端、输出端和耦合矩阵;cij表示能量从第i个能源转换到第j个能源的效率。
本文所讨论的能源集线器如图2所示,可以看到,能源集线器的输入和输出均为电、气和热,明显可以看出电气热系统中的潮流方向。该能源集线器包含5种设备:变压器(T)、空调(AC)、天然气管道(GP)、热电联产机组(CHP)和热交换器(HE),AC和CHP是耦合设备,能源集线器的耦合矩阵为:

式中:Le、Lg、Lh、Pe、Pg和Ph分别为能源集线器的电气热三输出和三输入;η是设备能量转化的效率;v是与电气热能源分配有关的调度因子,ve,T + ve,AC = 1。
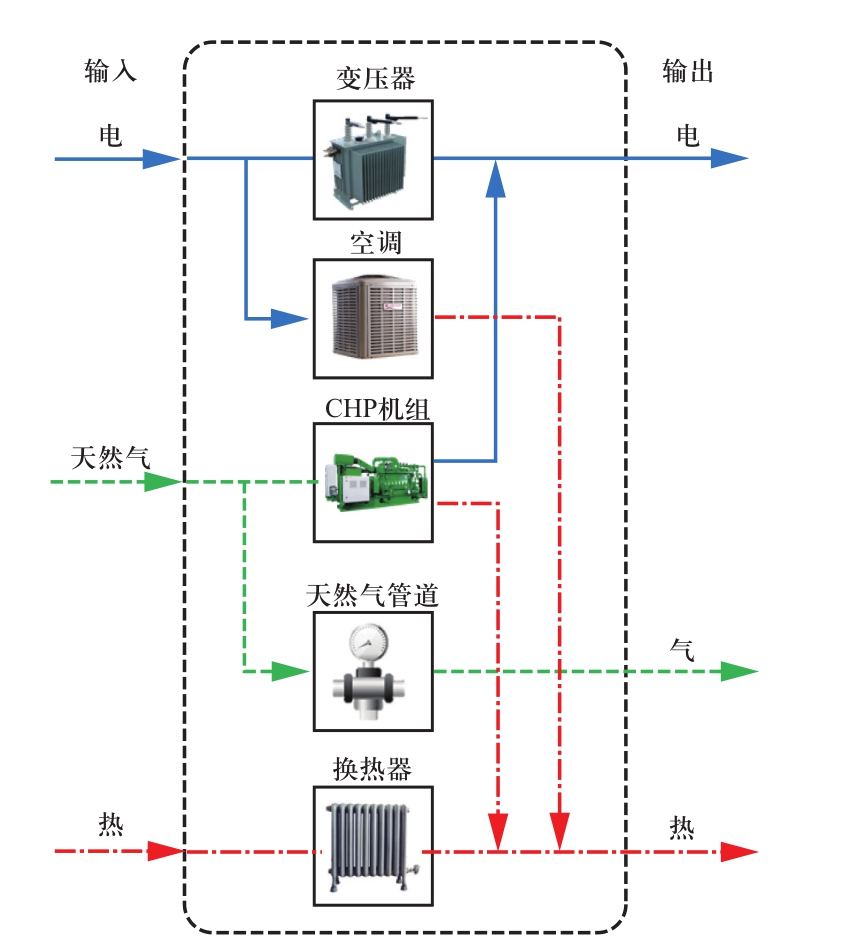
图2 能源集线器结构图
Fig.2 Structure of energy hub
能源集线器优化调度模型同样以负荷削减量最低为目标函数:
式中:NEH为耦合节点即能源集线器的数量;i为能源集线器标号;e、g、h分别为电/气/热三种能源;ΔL为能源集线器电/气/热输出负荷削减量。其约束条件为:
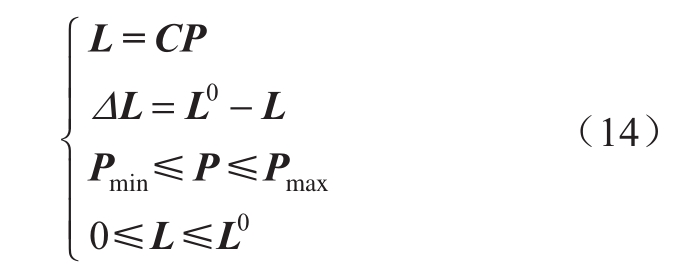
式中:Pmin和Pmax为P的下限值和上限值;L0为最初输入的能源集线器电/气/热负荷。
2 综合能源系统最优负荷削减算法
2.1 综合能源系统分层解耦的最优负荷削减模型
解耦求解法利用现有成熟的潮流求解方法对各能源子系统进行独立求解,再基于能源集线器求解能源耦合方程,求解灵活且易于收敛。本文基于解耦求解法的思路,给出了综合能源系统基于分层解耦的最优负荷削减算法。
图3为综合能源系统分层解耦的最优负荷削减模型(hierarchical decoupling optimal load curtailment framework, HDOLCF),模型分为外层和内层,内层分别对电气热能源子系统进行以负荷削减量最小为目标的最优潮流(OPF)计算,外层则利用能源集线器对综合能源系统中电气热三种能源进行整体优化调度,从而体现三种能源的互补转化关系,通过内外两层模型的不断迭代求解,得到最终收敛解。该模型可将综合能源系统最优负荷削减问题转化为单一的OPF问题,极大地降低了原问题的复杂性,显著提高了计算效率、稳定性和实用性。
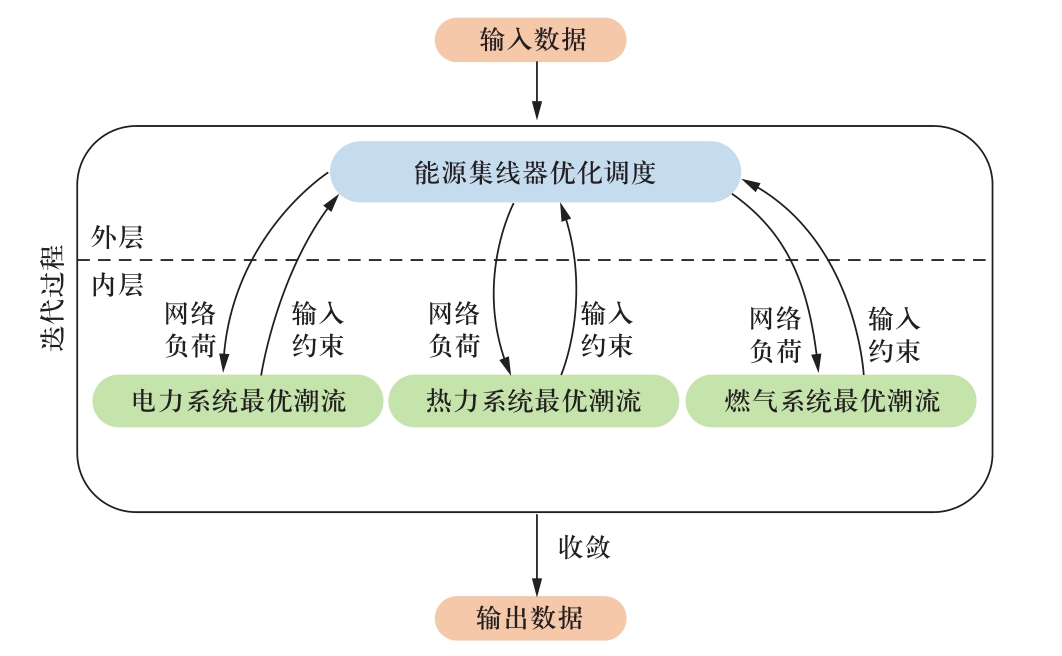
图3 综合能源系统分层解耦的最优负荷削减模型
Fig.3 HDOLCF in IES
2.2 综合能源系统可靠性评估方法
综合能源系统分层解耦的最优负荷削减量计算方法是综合能源系统可靠性评估方法的重要部分。目前传统可靠性评估方法主要有两种:状态枚举法(SE)和蒙特卡洛法(MCS),两种方法各有其适用场合[19]。本文采用状态枚举法对综合能源系统进行可靠性评估。
状态枚举法先利用枚举算法选择系统状态,然后通过综合能源系统分层解耦的最优负荷削减量计算方法来定量评估所选择状态的负荷削减量,最后求得其总的数学期望,即可靠性指标。
状态枚举法中系统状态可表示为:
式中:ai和ui分别为第i个系统元件的可用率和不可用率;N是系统的元件总数。
系统状态s的概率P(s)为:
式中:Nf是系统状态s中失效元件的数量。
状态枚举法的可靠性指标R为:
式中:I(s)为状态s的影响函数即可靠性指标,如负荷削减等;Ω为系统状态集合。
可靠性指标由相应的状态影响函数I(s)确定,在实际工程中常采用EENS(expected energy not supplied) [20]作为可靠性评估指标,根据式(18)可得。
式中:T是可靠性评估的时间尺度;ILC(s)是综合能源系统状态s的负荷削减量。
2.3 综合能源系统可靠性评估算法流程
将分层解耦的最优负荷削减模型应用于状态枚举法,对电气热综合能源系统的可靠性评估,算法流程如图4所示。具体步骤为:
步骤1:输入综合能源系统数据,包括电/气/热系统和能源集线器等。
步骤2:设定综合能源系统分层解耦优化模型的收敛阈值δ、最大迭代次数NHDOF和故障状态枚举最高阶数N。初始化故障阶数k= 1。
步骤3:建立k阶故障状态集Ωsk,如下:
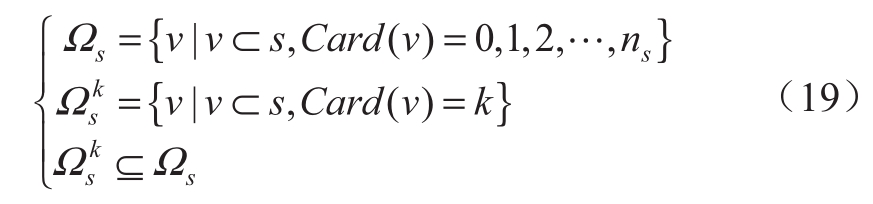
式中:Ωs是系统状态s的ns阶以内故障状态总集;Ωsk是Ωs的k阶故障状态子集;Card(a)表示状态v包括的故障元件数。当k= 0时,Ωsk = φ。
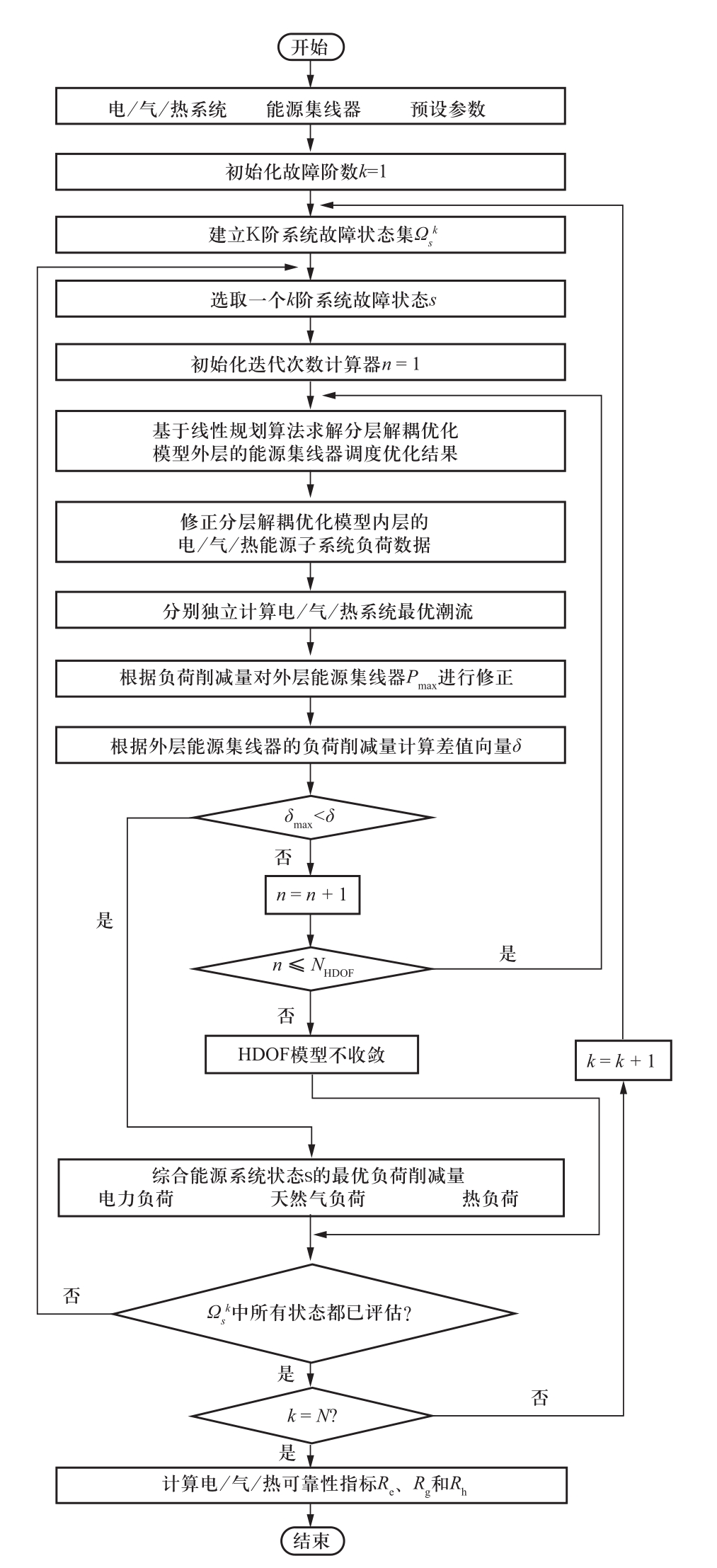
图4 综合能源系统可靠性评估算法流程图Fig.4 Flowchart of IES reliability assessment
步骤4:从k阶系统故障状态集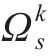 中选取综合能源系统故障状态s,对综合能源系统状态s的最优负荷削减量进行计算。
中选取综合能源系统故障状态s,对综合能源系统状态s的最优负荷削减量进行计算。
步骤5:初始化迭代次数计算器n = 1。
步骤6:结合式(13)和(14)求解分层解耦模型外层的能源集线器调度优化结果。
步骤7:根据能源集线器调度优化结果,修正分层解耦优化模型中内层各能源子系统的负荷:

式中:i∈EH表示电力系统节点i与能源集线器相连;i∉EH表示电力系统节点i与能源集线器不相连;j和k分别表示天然气系统和热力系统。
步骤8:分别求解电力系统负荷削减的最优潮流问题,见式 (1) 和 (2),天然气系统负荷削减的最优潮流问题,见式 (4) 和 (5),热力系统负荷削减的最优潮流问题,见式 (8) 和 (9),得到电/气/热能源子系统的最优负荷削减量。
步骤9:根据前一步计算得到的各能源子系统的最优负荷削减量修正外层模型中能源集线器输入P的上限值Pmax:
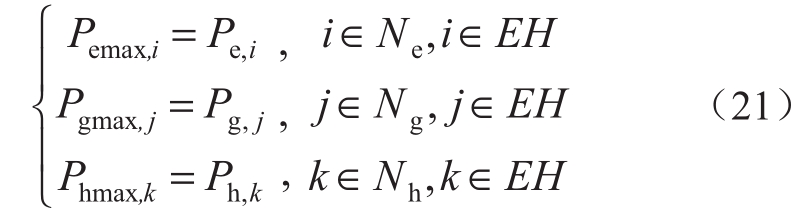
步骤10:根据步骤8得到的最优负荷削减量来计算判断模型是否收敛的δmax:
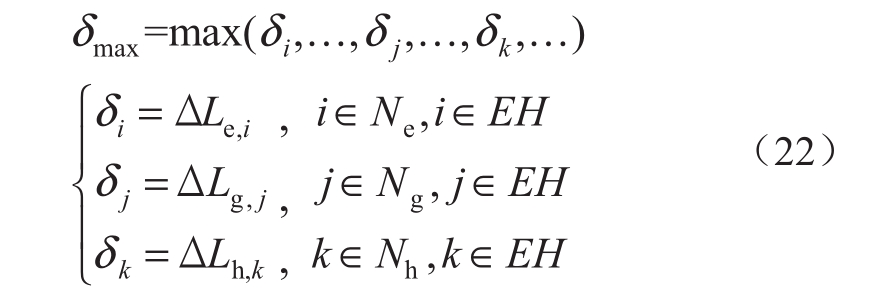
步骤11:若δmax<δ,转到步骤13;否则,进行下一步。
步骤12:迭代计数器n= n+1,若n<NHDOF,转到步骤6;否则,模型不收敛,转到步骤13。
步骤13:计算系统故障状态s下综合能源系统的电/气/热最优负荷削减量ΔLs,e、ΔLs,g和ΔLs,h:
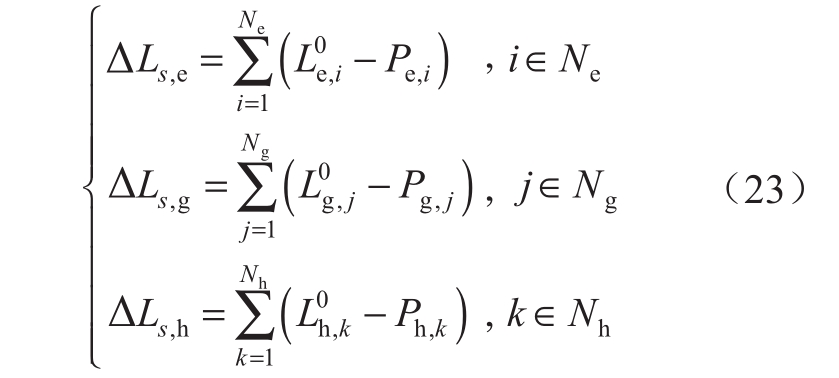
式中:L0是步骤1输入的综合能源系统初始各节点负荷数据,包括电/气/热能源子系统节点负荷和各能源集线器输出负荷;P是本轮迭代中步骤5所得到的最优负荷削减量计算结果。
步骤14:判断k阶故障状态是否分析完成,若是,继续下一步骤;若否,跳到步骤4。
步骤15:判断k是否等于N,若是,继续下一步骤;若否,k加1并跳到步骤3。
步骤16:基于式(17)计算电/气/热可靠性指标Re、Rg和Rh:

3 算例分析
本文综合能源系统算例由IEEE 33节点电力系统[21]、32节点热力系统[18]和14节点天然气系统[22]组成,如图5所示。年负荷曲线见文献[23]。IEEE 33节点系统发电出力容量为9 MW,峰值负荷为3.175 MW,32 节点热力系统出力容量为4.5 MW,峰值负荷为2.164 MW。14节点天然气系统出力容量为1.9 MW,峰值负荷为0.285 MW。压缩机由燃气轮机驱动,抽头位置为注气管道端。接入4个能源集线器,能源集线器电/气/热输入最大限制等于接入节点相应负荷的1.5倍,输出侧电气热负荷等于接入节点相应负荷。
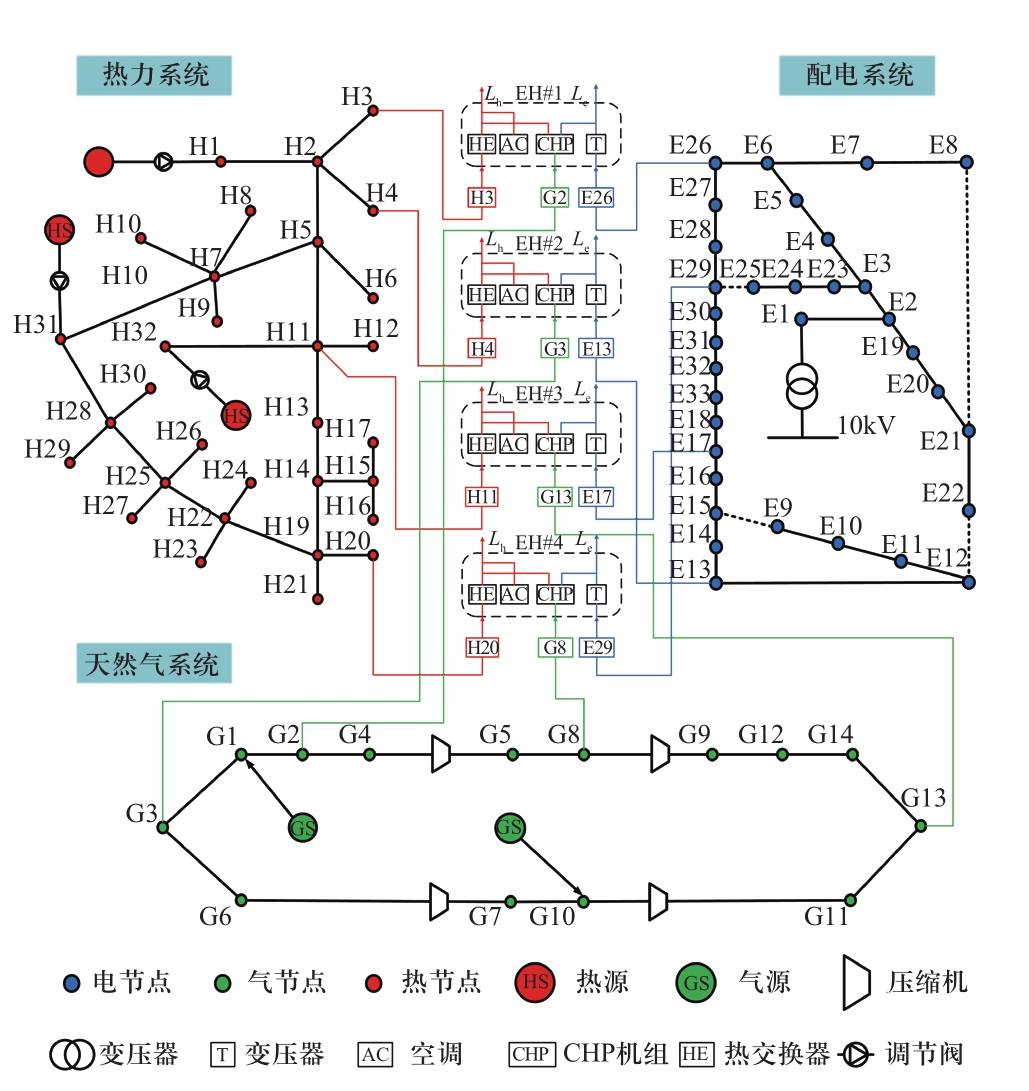
图5 综合能源系统测试算例
Fig.5 Test case of IES
本文将所提的电气热综合能源系统分层解耦最优负荷削减算法应用于可靠性评估中,求解分析线路故障状态下系统的可靠性水平,可靠性评估方法为状态枚举法,指标为EENS,状态枚举阶数为2,不可用率为0.1%。
3.1 耦合环节分析
区别于传统独立解耦的电/气/热系统,综合能源系统通过燃气轮机、空调等耦合元件将电/气/热等子系统联结起来形成一个整体系统,因此有必要分析综合能源系统耦合环节对可靠性的影响。能源集线器作为主要的耦合环节,本节主要分析能源集线器结构对可靠性的影响。
图5综合能源系统算例中设置了4个能源集线器,将此算例作为基础算例A1,改变能源集线器的内部结构,能源集线器中具有耦合作用的元件有空调(AC)和热电联产机组(CHP),空调具有电热耦合作用,热电联产机组具有电气热耦合作用,通过增删上述元件完成能源集线器内部结构的改变形成算例。算例A2在算例A1基础上删除热电联产机组,仅保留电热耦合元件空调;算例A3在算例A1基础上删除空调,仅保留电气热耦合元件热电联产机组;算例A4能源集线器仅保存元件变压器、天然气管道和热交换器,电/气/热子系统完全解耦。对算例A1—A4进行可靠性分析,结果见表1。
表1 不同耦合环节的可靠性评估结果
Table1 Reliability assessment of different coupling parts
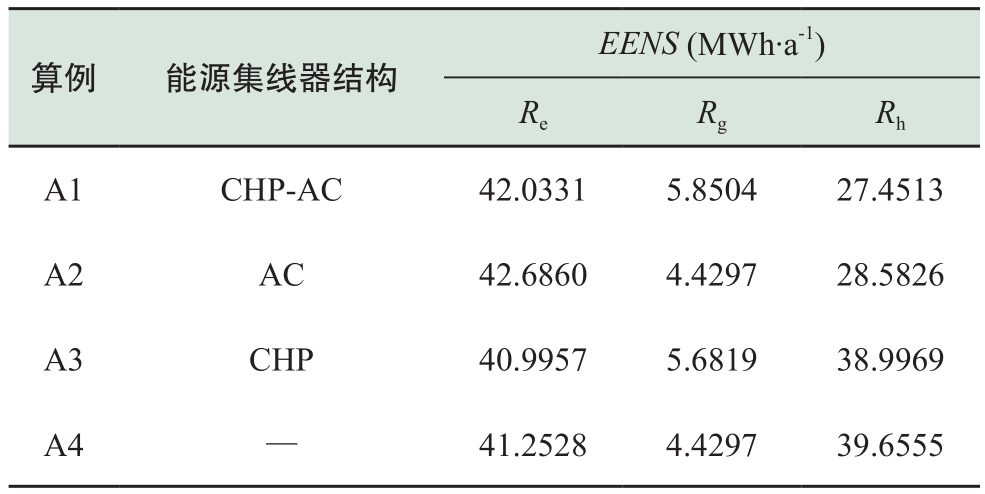
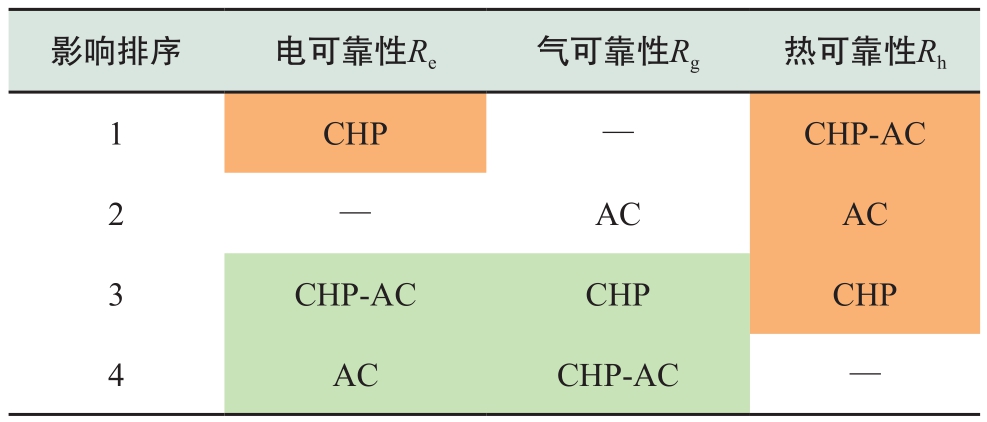
表1表明耦合环节对系统可靠性有重要影响。耦合环节能源集线器的结构设置不同,综合能源系统各子系统耦合关系不同,相应不同能源之间的转移转化过程不同,对可靠性的影响也会有区别。表2给出了表1各算例中能源集线器对应的能源子系统耦合关系,其中箭头表示能量流动方向。根据表1和表2得到不同能源集线器结构对电/热可靠性的影响能力并进行排序,见表3。
表3对能源集线器结构对可靠性影响能力进行排序,红色代表可靠性影响为正,即增强可靠性,绿色代表可靠性影响为负,即减弱可靠性。可以看出,AC和CHP可以将电和气转化为热,所以引入能源集线器结构后,将电力系统、天然气系统和热力系统耦合起来,对热可靠性有很大的提升。但为了补充热负荷,会加重电负荷和天然气负荷,有可能会导致气可靠性或电可靠性的下降。
表2 能源子系统耦合关系
Table2 Coupling relationship of energy subsystem
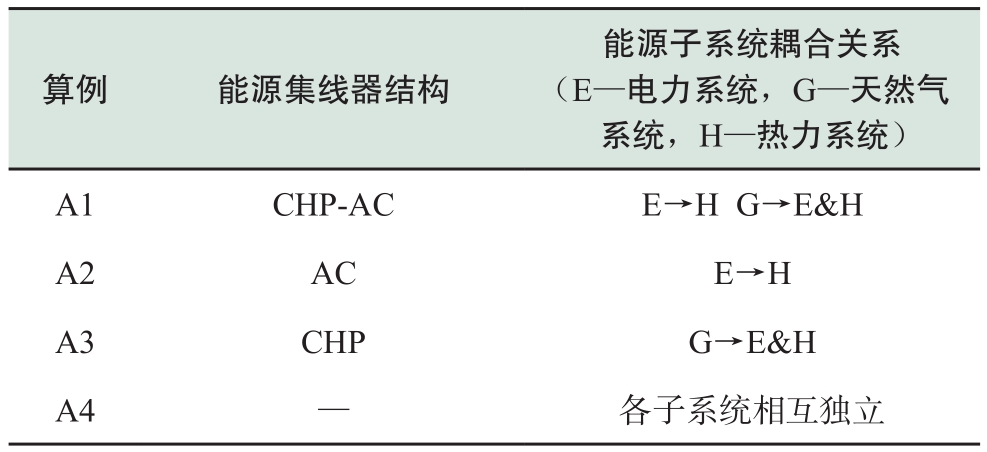
表3 耦合环节对可靠性的影响能力
Table3 The order of the impact of coupling parts on reliability
3.2 薄弱环节分析
通过系统可靠性分析,发现系统内的薄弱环节并予以加强是可靠性评估的重要功能。通过分层解耦的电气热最优负荷削减模型,各电气热子系统可被独立分析。本节对电力线路、天然气管道和热力管道进行薄弱环节分析,确定相应的薄弱环节,为下一步系统可靠性的提升提供参考。
图6、7和8分别给出了电、气、热可靠性的薄弱环节分析结果:电可靠性指标EENS主要由电力线路故障导致,薄弱环节为电力线路1和2,其中电力线路LE1是算例图5中配网系统电源供应的唯一通道,是极为重要的线路;天然气系统拓扑结构呈环状,环内的各条线路都对可靠性有着重要影响,PG1、PG4和PG6都是影响较大环节,其中PG6是影响最大的薄弱环节;热力系统整体结构成环,且局部放射,大多数元件都对可靠性有着重要影响。在故障影响较大的管道中,PH13、PH30和PH31处于热网环结构中,PH5、PH7等管道位于局部放射状结构中,故障直接影响其相连负荷的供给能力,可认为PH13、PH30和PH31是热力系统的主要薄弱环节。

图6 电可靠性的薄弱环节分析
Fig.6 Weak point analysis in electricity reliability
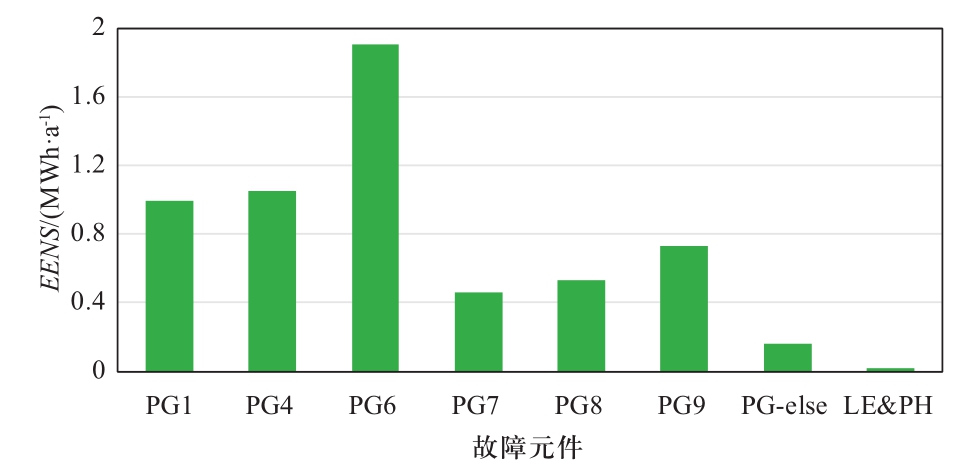
图7 气可靠性的薄弱环节分析
Fig.7 Weak point analysis in gas reliability
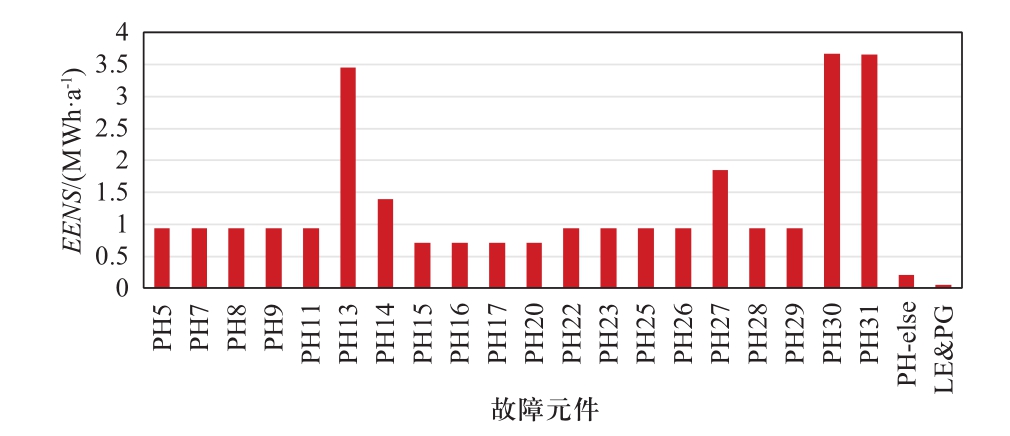
图8 热可靠性的薄弱环节分析
Fig.8 Weak point analysis in heat reliability
3.3 可靠性提升分析
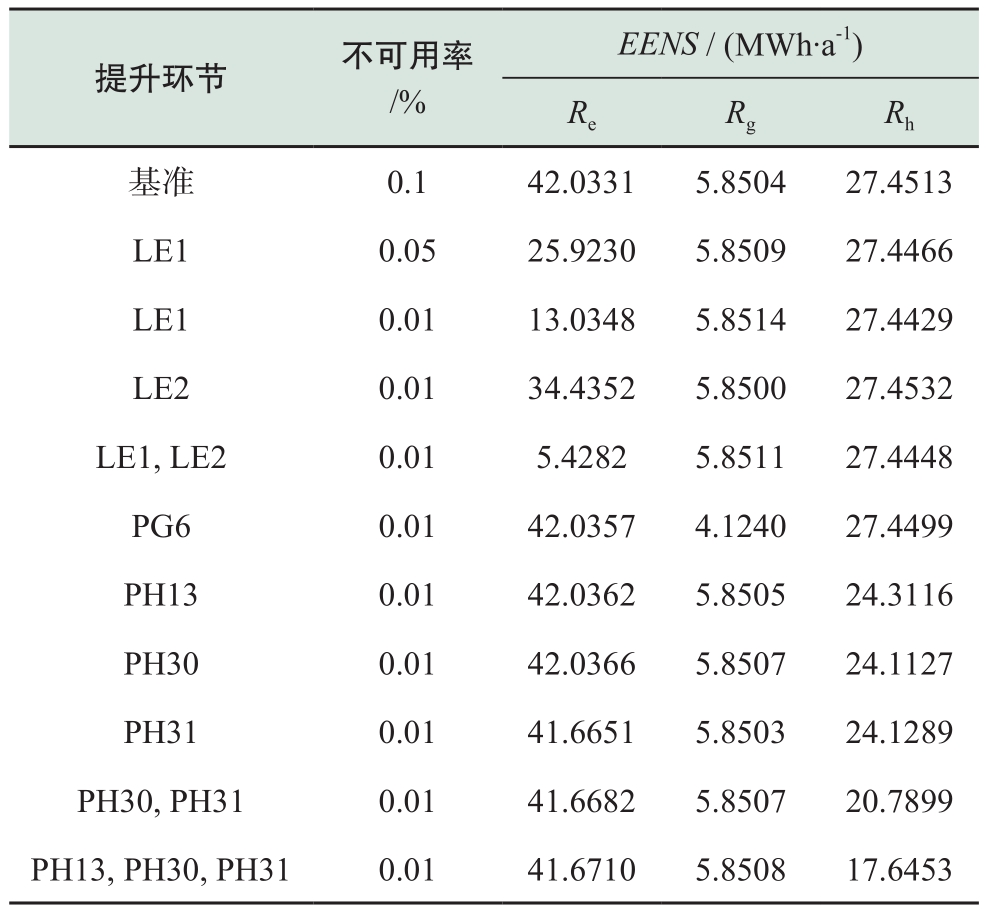
根据薄弱环节分析的结果,针对薄弱环节进行可靠性提升,采用检修计划优化、设备升级、备用线路架设等方式提高薄弱环节的可靠性,即降低元件的不可用率。对薄弱环节提升后的综合能源系统算例进行可靠性分析,结果见表4。
表4可以看出薄弱环节升级改造后,不同能源子系统可靠性的提升程度存在差异。电可靠性提升程度最大,这是由于电力线路LE1是电源出力唯一通道,是电可靠性指标EENS的主要来源。热可靠性的提升程度有限,因为算例热力系统中存在大量的发射状网络,仅仅对个别热力管道进行加强所产生的可靠性提升效果有限。
表4 可靠性提升分析结果
Table4 Results of reliability improvement
4 结论
最优负荷削减算法是综合能源系统可靠性评估的重要环节。本文给出了一种面向电气热综合能源系统可靠性评估的最优负荷削减量分层解耦计算方法,可以有效稳定地求解电气热综合能源系统在故障状态下的最优负荷削减量,从而对系统进行可靠性评估。利用该方法分析了不同能源耦合环节结构对系统电/气/热可靠性的影响能力,研究了多能源互补转化对可靠性的影响。结果表明,多能源耦合可以在整体上提升能源供给的可靠性,但也可能会降低部分能源子系统的可靠性。同时,也对系统进行了薄弱环节分析和相应可靠性提升分析。
未来的工作应将设备故障纳入系统故障状态考虑范围,同时考虑综合能源系统中分布式发电、储能和电动汽车等新能源新技术对系统可靠性的影响。
参考文献
[1]贾宏杰,穆云飞,余晓丹.对我国综合能源系统发展的思考[J].电力建设,2015,36(1):16-25.
Jia Hongjie, Mu Yunfei, Yu Xiaodan.Thought about the integrated energy system in China[J].Electric Power Construction, 2015, 36(1): 16-25(in Chinese).
[2]贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.
Jia Hongjie, Wang Dan, Xu Xiandong, et al.Research on some key problems related to integrated energy systems[J].Automation of Electric Power Systems, 2015, 39(7): 198-207(in Chinese).
[3]Lei Yunkai, Hou Kai, Wang Yue, et al.A new reliability assessment approach for integrated energy systems: using hierarchical decoupling optimization framework and impactincrement based state enumeration method[J].Applied Energy,2018, 210: 1237-1250.
[4]侯恺.电力系统可靠性评估方法改进与应用研究[D].天津:天津大学,2016.
Hou Kai.Power system reliability assessment methodology improvement and its application[D].Tianjin: Tianjin University, 2016(in Chinese).
[5]赵渊,周家启,刘洋.发输电组合系统可靠性评估中的最优负荷削减模型分析[J].电网技术,2004,28(10):34-37.
Zhao Yuan, Zhou Jiaqi, Liu Yang.Analysis on optimal load shedding model in reliability evaluation of composite generation and transmission system[J].Power System Technology, 2004, 28(10): 34-37(in Chinese).
[6]雷云凯.基于影响增量的电力系统及综合能源系统可靠性评估方法[D].天津:天津大学,2018.
Lei Yunkai.Impact-increment based reliability assessment method for power system and integrated energy system[D].Tianjin: Tianjin University, 2018(in Chinese).
[7]Geidl Martin, Andersson Goran.Optimal coupling of energy infrastructures[C]//2007 IEEE Lausanne Power Tech,Lausanne, Switzerland, July 1-5, 2007.
[8]Geidl Martin, Koeppel Gaudenz, Favre-Perrod Patrick, et al.Energy hubs for the future[J].IEEE Power and Energy Magazine, 2007, 5(1): 24-30.
[9]林威,靳小龙,穆云飞,等.区域综合能源系统多目标最优混合潮流算法[J].中国电机工程学报,2017,37(20):5829-5839.
Lin Wei, Jin Xiaolong, Mu Yunfei, et al.Multi-objective optimal hybrid power flow algorithm for integrated local area energy system[J].Proceedings of the CSEE, 2017, 37(20):5829-5839(in Chinese).
[10]Lei Yunkai, Zhang Pei, Hou Kai, et al.An incremental reliability assessment approach for transmission expansion planning[J].IEEE Transactions on Power Systems, 2018,33(3): 2597-2609.
[11]Liu Xuezhi, Wu Jianzhong, Jenkins Nick, et al.Combined analysis of electricity and heat networks[J].Applied Energy,2016, 162: 1238-1250.
[12]王伟亮,王丹,贾宏杰,等.考虑运行约束的区域电力-天然气-热力综合能源系统能量流优化分析[J].中国电机工程学报,2017,37(24):7108-7120.
Wang Weiliang, Wang Dan, Jia Hongjie, et al.Analysis of energy flow optimization in regional electricity-gas-heat integrated energy system considering operational constraints[J].Proceedings of the CSEE, 2017, 37(24): 7108-7120(in Chinese).
[13]Shao Chengcheng, Wang Xifan, Shahidehpour Mohammad, et al.An MILP-based optimal power flow in multicarrier energy systems[J].IEEE Transactions on Sustainable Energy, 2017,8(1): 239-248.
[14]余晓丹,徐宪东,陈硕翼,等.综合能源系统与能源互联网简述[J].电工技术学报,2016,31(1):1-13.
Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al.A brief review to integrated energy system and energy internet[J].Transactions of China Electrotechnical Society, 2016, 31(1):1-13(in Chinese).
[15]Martinez-Mares Alberto, Fuerte-Esquivel Claudio.A unified gas and power flow analysis in natural gas and electricity coupled networks[J].IEEE Transactions on Power Systems,2012, 27(4): 2156-2166.
[16]Ouyang Liang-biao, Aziz Khalid.Steady-state gas flow in pipes[J].Journal of Petroleum Science & Engineering, 1996,14(3-4): 137-158.
[17]孙国强,陈霜,卫志农,等.计及相关性的电-气互联系统概率最优潮流[J].电力系统自动化,2015,39(21):11-17.
Sun Guoqiang, Chen Shuang, Wei Zhinong, et al.Probabilistic optimal power flow of combined natural gas and electric system considering correlation[J].Automation of Electric Power Systems, 2015, 39(21): 11-17(in Chinese).
[18]Liu Xuezhi.Combined analysis of electricity and heat networks[D].Cardiff: Cardiff University, 2013.
[19]Billinton R, Allan R N.Power-system reliability in perspective[J].Electronics and Power, 1984, 30(3): 231-236.
[20]Hou Kai, Jia Hongjie, Yu Xiaodan, et al.An impact incrementsbased state enumeration reliability assessment approach and its application in transmission systems[C]//2016 IEEE Power and Energy Society General Meeting, Boston, USA, July 17-21, 2016.
[21]Mohamed Imran, Kowsalya M.A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using Fireworks Algorithm[J].International Journal of Electrical Power & Energy Systems,2014, 62: 312-322.
[22]Wang Jiangjiang, Fu Chao, Yang Kun, et al.Reliability and availability analysis of redundant BCHP (building cooling,heating and power) system[J].Energy, 2013, 61: 531-540.
[23]Probability Methods Subcommittee.IEEE reliability test system[J].IEEE Transactions on Power Apparatus and Systems.1979, PAS-98(6): 2047-2054.
Hierarchical Decoupling Optimal Load Curtailment Algorithm for Integrated Energy Systems Reliability Evaluation
ZHAO Changwei1, ZHANG Huiying1, LIU Chunling1, GAO Jiaxin1, LIU Zeyu2, HOU Kai2*, JIA Hongjie2
(1.Chengdong Power Supply Company, State Grid Tianjin Electric Power Company, Hedong District, Tianjin 300250, China;2.Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Nankai District, Tianjin 300072, China)
Abstract: Energy security is a critical issue that is related to the national economy and people’s livelihood.The basic task of an integrated energy system, the core of a future energy system, is to supply safe and reliable energy.In this study, a hierarchical decoupling optimal load curtailment algorithm for integrated energy system reliability evaluation is proposed to solve the problem associated with the traditional optimal load curtailment algorithm, namely difficulty of converging.The optimal dispatch of energy hubs and the optimal power flow of electricity, gas,and heat subsystems are uncoupled and calculated based on a hierarchical decoupling optimal load curtailment framework,and the optimal load curtailment of an integrated energy system is obtained under various fault states.This approach can be employed for power-gas-heat integrated energy system reliability evaluation as demonstrated with numerical examples;it reasonably reflects the impact of complementation and transformation of electricity, gas, and heat on system reliability under various fault states, and is also suitable for weak point analysis and reliability improvement planning.
Keywords: integrated energy system; reliability assessment; optimal load curtailment algorithm; hierarchical decoupling framework
文章编号:2096-5125 (2019) 06-0538-09
中图分类号:TK01;TE09
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.06.003
基金项目:国网天津市电力公司科技项目(智慧园区与智慧小镇关键技术构架及运营模式研究,KJ19-1-03)。
State Grid Tianjin Electric Power Company Technology Project(Research on Key Technology Architecture and Operation Model of Intelligent Park and Intelligent Town, KJ19-1-03).
收稿日期:2019-06-30;修回日期:2019-07-31。
作者简介:

赵长伟
赵长伟(1982),男,高级工程师,主要研究方向为电力系统规划,综合能源系统可靠性分析,E-mail:tchengdongface@163.com。
张慧颖(1990),女,工程师,主要研究方向为综合能源系统规划,E-mail:hyzhang@163.com。
刘春玲(1982),女,高工,主要研究方向为电网投资规划,E-mail:clliu@163.com。
侯恺(1988),男,博士,硕士生导师,主要研究方向为电力系统风险评估、综合能源系统。通信作者,E-mail:khou@tju.edu.cn。
(责任编辑 李锡)