0 引言
柔性直流输电(flexible high voltage direct current transmission, flexible HVDC)技术具有结构灵活、可控性高、输出谐波小等特点[1],为实现风电大规模远距离输送提供了理想的解决方案。上海南汇柔直、广东南澳柔直、欧洲北海BorWin1柔直等国内外多个用于风电送出的柔性直流输电工程相继投产。但风电和柔性直流输电系统均基于电力电子变流器,存在因控制相互作用而引发的系统振荡风险。上述柔直工程在调试或运行过程中曾出现过几赫兹至上千赫兹的功率振荡现象[2-4]。与传统电力系统振荡不同,这种变流器参与的新型功率振荡表现出电磁暂态时间尺度下的宽频带特性,其机理复杂,已成为学者和电力科研单位研究的热点[5-6]。
文献[7]报导了一种双馈风电场经柔性直流并网的次同步振荡现象,分析了次同步振荡电流在柔性直流系统中的分布与传播机制,但该文并未对振荡机理进行建模分析。借鉴传统电力系统稳定性分析思路,文献[8]建立了包含两电平电压源变流器(voltage source converter,VSC)的双馈风电机组小信号模型,研究不同控制模式和参数下风电系统小干扰稳定性。文献[9]建立包含模块化多电平换流器(modular multilevel converter, MMC)阀及其控制系统的详细小信号模型,对MMC内部模态及相应影响因素进行了详细分析。然而,利用特征根分析法研究的对象主要是单个模型或简单系统,当系统规模增大、结构复杂时,会出现“维数灾”问题,不易推广到含多变流器的风电经柔性直流并网系统。
基于频域的阻抗特性分析方法[10]是一种分析复杂电力电子系统稳定性简单而有效的方法。其基本原理是通过构建互联系统中各子系统的戴维南(或诺顿)等效阻抗模型,根据奈奎斯特或相角裕度等稳定性判据[11-12]分析系统潜在的谐振频率及稳定裕度。在阻抗建模基础上,文献[13]利用奈奎斯特稳定性判据,分析了风机变流器电流环、锁相环参数及VSC-HVDC电压电流控制对系统稳定性的影响,指出加快VSCHVDC送端电压外环控制速度或者减慢风机锁相环控制速度能够提高系统稳定性。文献[14]通过分析奈奎斯特曲线的变化规律,进一步提出当VSC-HVDC送端换流站控制带宽小于风机网侧逆变器控制带宽时系统发生次同步振荡。相比于两电平VSC,MMC具有环流抑制等更复杂结构。文献[15]初步建立了MMC交流侧序阻抗模型,提出无环流控制时互联系统的稳定裕度较低且容易出现次同步振荡现象,而加入环流控制能够抑制内部谐振现象。在此基础上,文献[16]基于多谐波线性化方法推导出计及锁相环和环流控制的MMC交流侧序阻抗详细解析公式,为后续研究风机参与的互联系统的稳定性提供了基础。目前,对风电经柔性直流并网系统的振荡问题尚没有物理意义上的机理解释,并且在次同步频率范围和中高频范围振荡风险与控制系统的关系以及风机出力和台数的影响有待深入研究。
本文首先介绍了风机与柔性直流互联系统阻抗模型,借鉴电路阻尼概念,推导互联系统的等效电路阻尼稳定性判据,并从物理意义解释互联系统发生振荡的机理。分析双馈风机网侧变流器控制带宽、锁相环控制带宽以及送端柔性直流换流站控制带宽与互联系统等效电路阻尼特性的关系,研究控制参数变化对宽频域范围振荡特性的影响。考虑风速和并网风机台数的影响因素,给出不同风机出力和风机台数的互联系统等效电路阻尼特性,提出考虑振荡稳定性的控制参数设计要求。
1 互联系统阻抗建模
风电经柔性直流并网的典型拓扑如图1所示。柔性直流输电系统为两端MMC-HVDC结构,由MMC换流站、换流变压器、直流线路组成;风电场由风机和箱变构成,可利用单机聚合的方法进行等值建模,风电场经升压变压器和汇集线路接入公共连接点(point of common coupling, PCC);受端交流电网可利用戴维南等值建模实现。
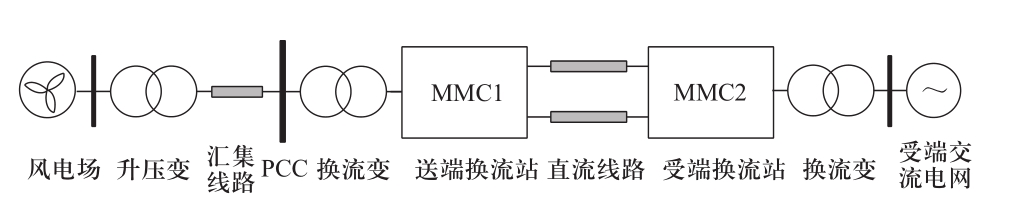
图1 风电经柔性直流并网的系统拓扑结构
Fig. 1 Topology of wind farms integration via an MMC-based HVDC system
为分析这种互联系统发生次、超同步振荡问题,在关注工况的稳态运行点建立基于频域阻抗的小信号模型。对于风机或MMC的“白箱”系统,采用机理建模法得到出口处电压Δui和电流Δii的关系[17-18]
经数学推导,其序阻抗模型均可写成如下形式
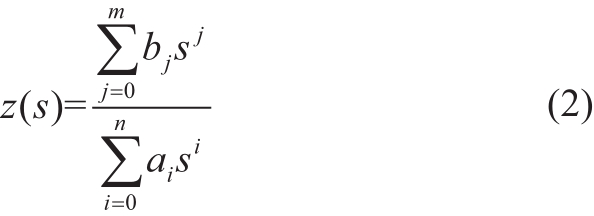
而对于“黑箱”系统可根据实验测量数据利用模型辨识法[18]得到序阻抗模型。
因此,以PCC点为界,图1所示的互联系统可分为风机侧子系统和柔直侧子系统,其等效序阻抗模型如图2所示。其中,柔直侧子系统等效为电压源UM、换流站阻抗ZMMC和换流变阻抗ZT,风机侧子系统等效为电流源Iw、风机阻抗Zwind和汇集线路阻抗Zgrid。

图2 互联系统等效阻抗模型
Fig. 2 Impedance model of interconnected system
2 等效电路阻尼稳定性判据

在s域下,式(3)中![]() 可视为形如
可视为形如![]() )的闭环传递函数。在分析稳定性时,常利用开环传递函数M(s) N(s)的幅频特性与相频特性,通过相角裕度稳定性判据来分析系统稳定性,系统稳定条件可表示为对于
)的闭环传递函数。在分析稳定性时,常利用开环传递函数M(s) N(s)的幅频特性与相频特性,通过相角裕度稳定性判据来分析系统稳定性,系统稳定条件可表示为对于

于是,有

由式(11)和式(13)可得,无论XM(ω)和Xw(ω)为感性或容性,当Rw(ω)+RM(ω)>0时,系统在谐振点ωa(此时|ZM(jωa)|=|Zw(jωa)|)均可保持稳定。因此,基于等效电路阻尼的互联系统稳定判据为当|ZM(jω)|=Zw(jω)|∀ω,都有RƩ(jω)>0,即系统稳定。其中,RƩ(jω)=RM(jω)+RW(jω)。
等效电路阻尼判据可理解为互联系统在谐振频率点若具有正阻尼,则系统稳定;若具有负阻尼,则系统存在功率振荡风险。相比于式(4)、(5)的相角裕度判据或奈奎斯特判据,等效电路阻尼判据体现出更直接的物理意义,并且根据子系统的阻尼特性可分辨其对引发振荡的贡献。值得注意的是,当子系统含有串联大电阻等特殊情况使得等效电阻值接近等效电抗值时,子系统等效阻抗频率曲线交点处互联系统等效电阻之和不再能准确地体现阻尼特性,等效电路阻尼判据的适用性变弱。|
3 振荡风险与控制系统的关系
为分析控制系统引发互联系统振荡的风险,在图1所示的拓扑基础上搭建具体的系统模型。MMCHVDC的额定直流电压为500 kV,额定传输容量为1500 MW,柔直换流器、换流变、直流线路等一次参数参照文献[19]中张北—北京正极系统进行设置。风电场输出功率为1050 MW,由700台1.5 MW的双馈风机构成,通过0.69 kV/35 kV箱变和35 kV/230 kV升压站接入PCC点。MMC1控制参考值为交流电压188 kV和交流频率50 Hz,MMC2控制参考值为直流电压500 kV和无功功率0 MVar。
在PCC点加入等效电路阻尼测量模型,如图3所示,通过扫描设置模块控制扰动源的幅值和频率,由系统阻尼特性分析模块提取两侧对应扰动源频率的电压、电流幅值并计算|ZM|、|Zw|和RƩ,以实施等效电路阻尼稳定性判据。在1~100 Hz频段以及100~1000 Hz谐振点附近频段设置1 Hz扫描频率间隔,而在其余频段设置10 Hz扫描频率间隔,以保证等效电路阻尼测量准确性,同时兼顾测量效率。
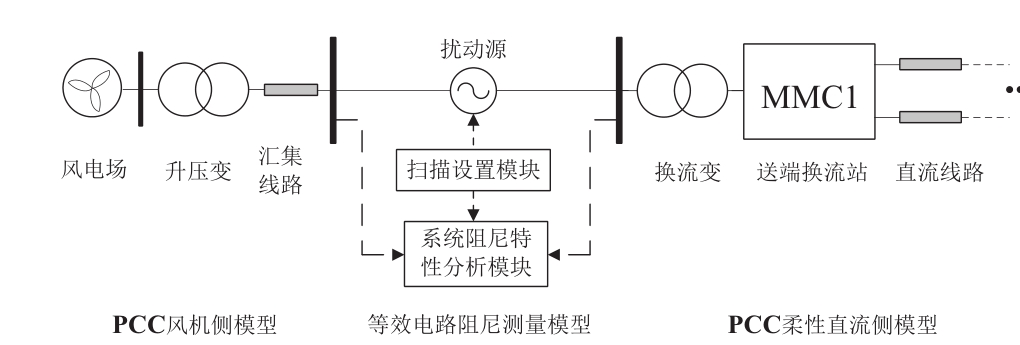
图3 互联系统等效电路阻尼测量示意图
Fig. 3 the Equivalent circuit damping measurement of the interconnected system
由于双馈风机的网侧变流器和送端MMC换流站连接作用至PCC点,其控制系统直接影响PCC点功率振荡风险,这里重点研究风机网侧变流器控制带宽、风机锁相环控制带宽以及送端MMC换流站控制带宽的影响。
3.1 风机网侧变流器控制带宽
由于风机网侧逆变器直流电压控制带宽较窄,因此电流控制带宽占主导地位。将电流控制比例增益调小(Kp=0.4)以使控制带宽变窄,互联系统的等效电路阻尼判定结果如图4(a)所示。可见,|Zw(jω)|在11.1 Hz和88.9 Hz出现谐振峰,并在11 Hz和89 Hz与|ZM(jω)|曲线相交,其交点处的RƩ(jω)分别为-0.07 Ω和-2.51 Ω。由于风机侧子系统和柔直侧子系统的等效电阻值均远小于等效电抗值,因此等效电路阻尼稳定性判据具有有效性,由图4(a)可见系统负阻尼由风机侧提供。此工况下互联系统在11 Hz和89 Hz附近具有谐振点且呈现负阻尼特性,而在100~1000 Hz均呈现正阻尼特性,系统存在次同步频率范围的功率振荡风险。经时域仿真,流经PCC点的a相电流含有3%的11 Hz谐波分量、10%的89 Hz谐波分量,如图4(b)所示,其结果与阻抗分析一致。
继续减小风机网侧逆变器电流控制比例增益(Kp=0.4,Kp=0.3,Kp=0.1),互联系统等效电路阻尼特性如图4(c)所示。可见,随着风机网侧逆变器控制带宽变窄,风机侧阻抗的谐振峰均处于0~100 Hz范围且具有远离基频的变化趋势,故振荡频率在0~100 Hz范围内愈发远离基频。
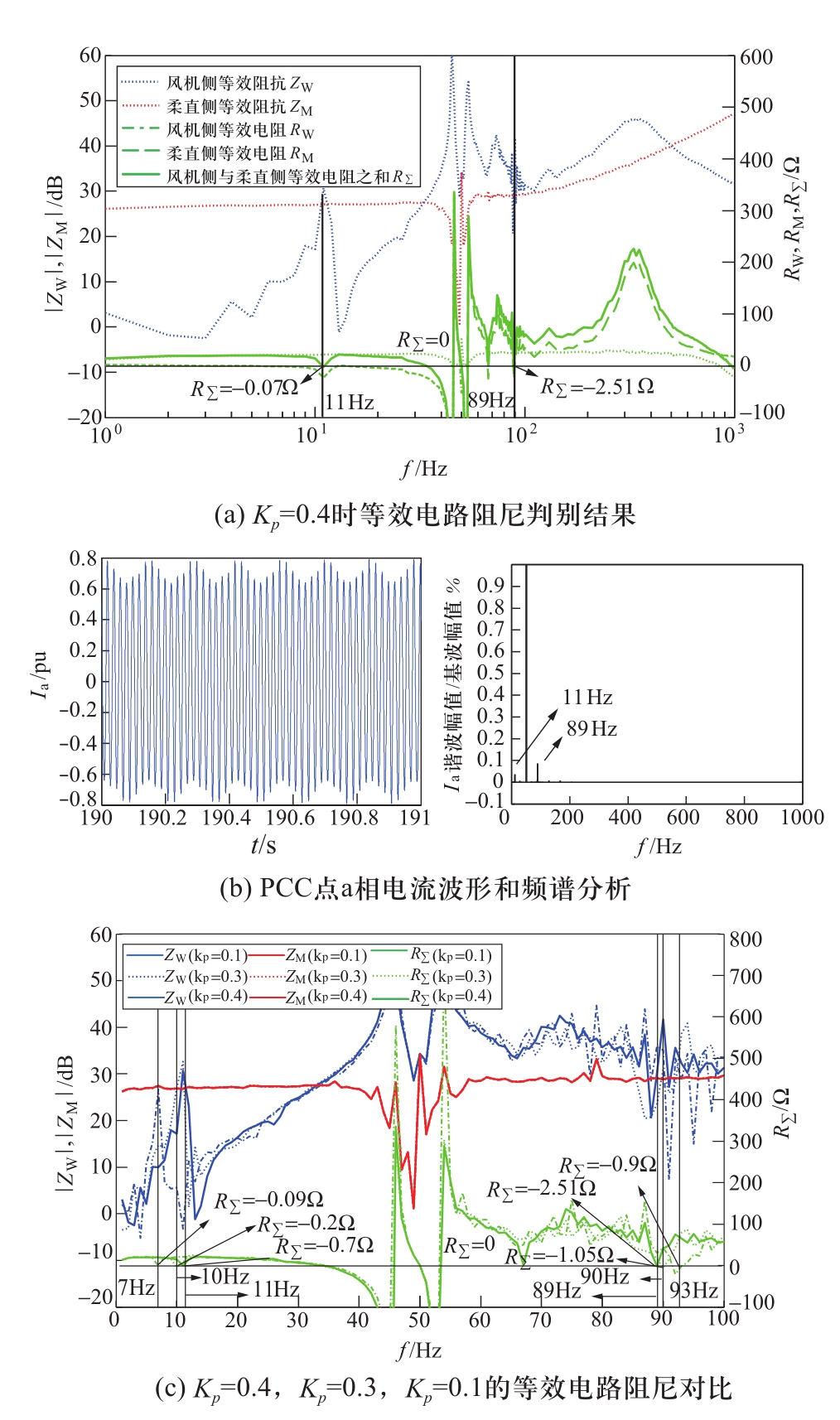
图4 风机网侧变流器控制带宽变窄的振荡分析结果
Fig. 4 Result of oscillation analysis of smaller control bandwidth of the network side converter
当风机网侧变流器控制带宽变宽时,系统振荡特性将发生改变。图5(a)给出了电流控制比例增益Kp=60时系统的等效电路阻尼特性。可见,|Zw(jω)|在300 Hz~400 Hz存在谐振峰并在380 Hz与|ZM(jω)|曲线相交,其交点处的RƩ(jω)为-2.57 Ω,且负阻尼同样由风机提供。因此,此工况下互联系统在380 Hz附近具有谐振点且呈现负阻尼特性,而在0~100 Hz均呈现正阻尼特性,系统存在中高频范围的振荡风险。经时域仿真,流经PCC点的a相电流含有3%的380 Hz谐波分量,如图5(b)所示,验证了阻抗分析结果。
继续增大风机网侧逆变器电流控制比例增益(Kp=60,Kp=120,Kp=150),互联系统等效电路阻尼特性如图5(c)所示。可见,随着风机网侧逆变器控制带宽变宽,系统在中高频范围出现负阻尼和谐振点的频率越高,故系统可能引发的振荡频率越高。
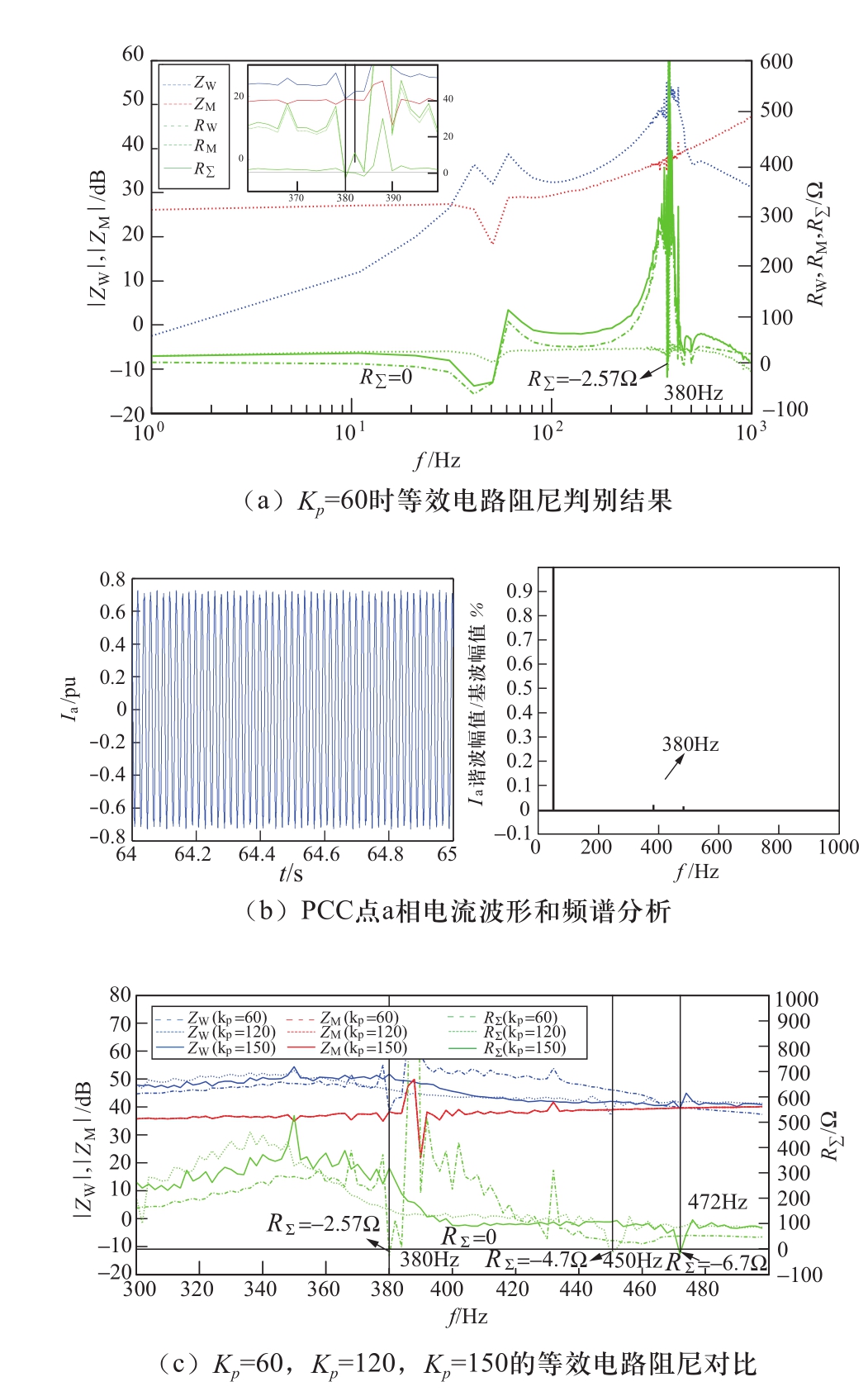
图5 风机网侧变流器控制带宽变宽的振荡分析结果
Fig. 5 Result of oscillation analysis of bigger control bandwidth of the network side converter
3.2 风机锁相环控制带宽
风机锁相环为网侧变流器提供坐标变换基准,其控制带宽将影响风机的阻抗特性。增大PLL控制比例增益(Kpll=40,Kpll=80),PLL控制带宽变宽,锁相速度变快,互联系统的等效电路阻尼判定结果如图6(a)所示。|Zw(jω)|在1 Hz~100 Hz产生谐振峰,并在与|ZM(jω)|曲线相交处呈现负阻尼特性。经时域仿真,对于Kpll=40工况,流经PCC点的a相电流含有5%的37 Hz谐波分量、2%的63 Hz谐波分量,如图6(b)所示,其结果与阻抗分析一致。并且,随着PLL控制带宽的增加,系统负阻尼和谐振点的频率在0~100 Hz呈现远离基频的趋势。
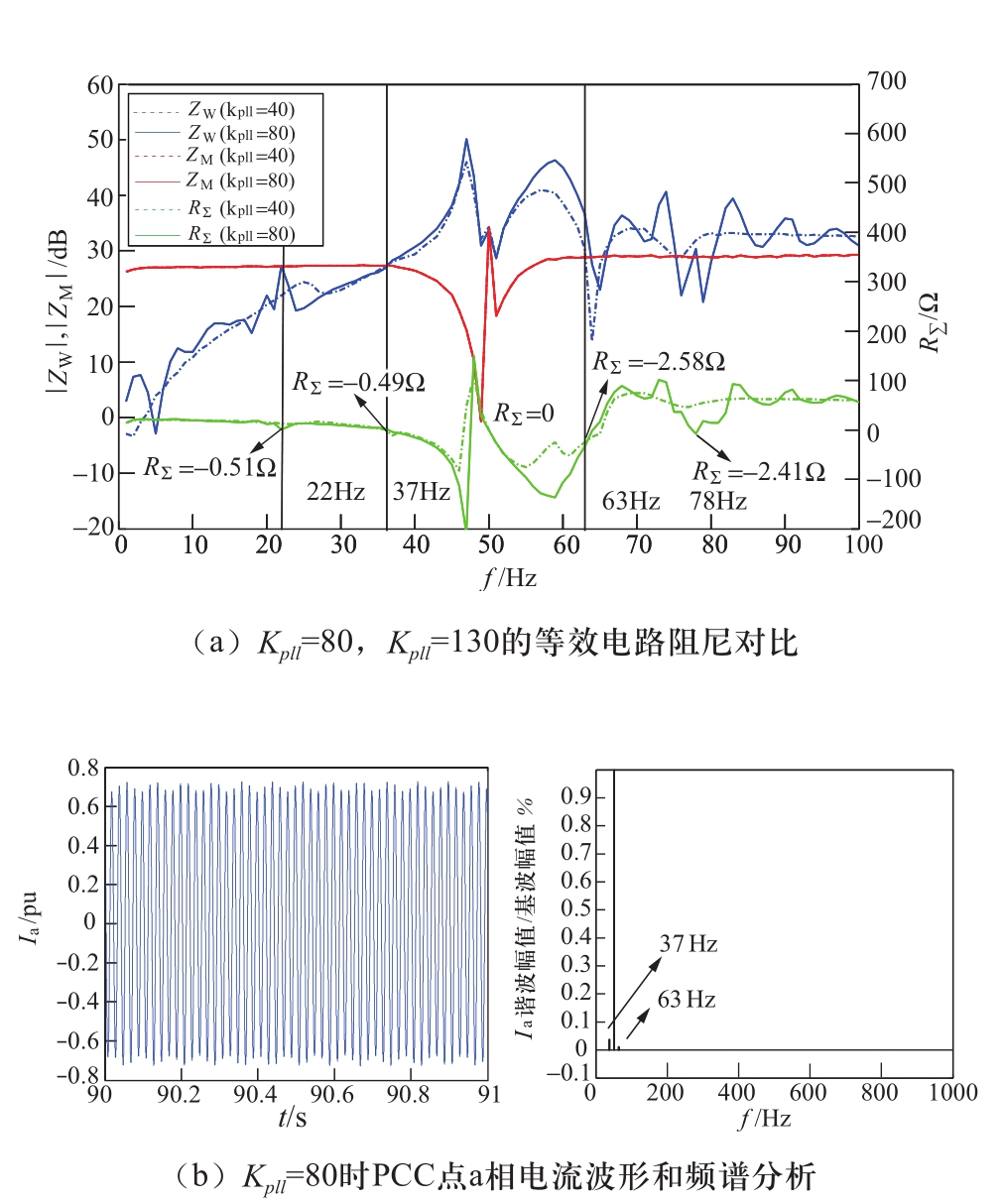
图6 风机锁相环控制带宽变化的振荡分析结果
Fig. 6 Result of oscillation analysis of control bandwidth of the PLL
3.3 送端MMC控制带宽
送端MMC的控制目标是维持PCC点交流电压的稳定,交流电压控制环节会直接影响控制响应性能,本节重点关注电压闭环控制,通过改变电压控制比例增益来分析送端MMC控制带宽对互联系统稳定性影响。增大电压控制比例增益(KM=20)或减小电压控制比例增益(KM=0.5)使MMC电压控制带宽改变时,互联系统的等效电路阻尼特性如图7(a)所示。可见,Kp=20时|Zw(jω)|在9 Hz和520 Hz与|ZM(jω)|曲线相交,其交点处的RƩ(jω)分别为-0.64 Ω和-2.04 Ω。因此,此工况下互联系统在9 Hz和520 Hz附近存在振荡风险,与图7(b)的时域仿真结果一致。当送端MMC电压控制带宽变小时,|ZM(jω)|曲线有上移的趋势,系统会有次同步范围内的振荡风险。因此,MMC控制带宽的调大调小表现为不同的阻尼特性,控制带宽过小时不会引发中高频范围的振荡。
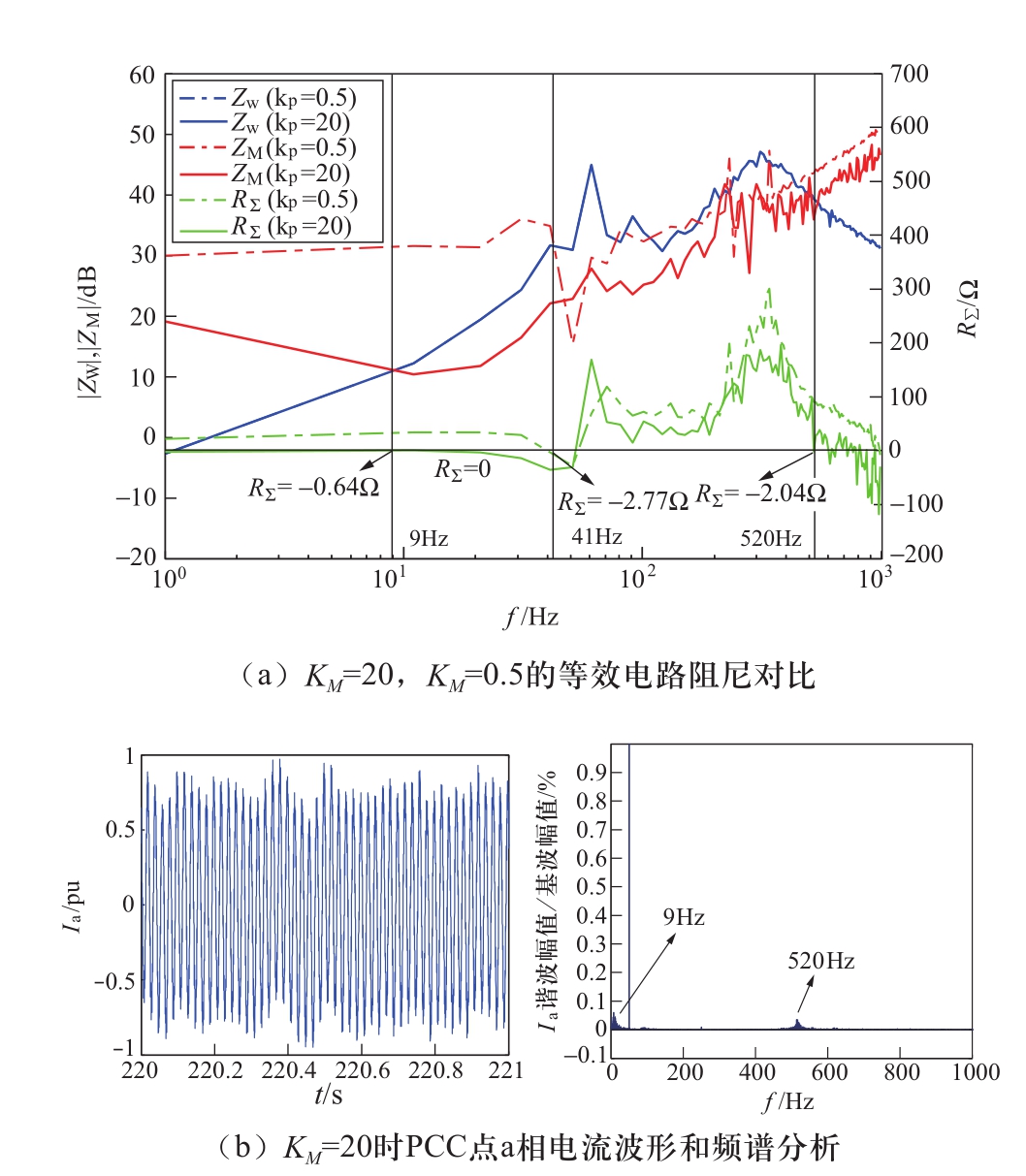
图7 送端MMC控制带宽变化的振荡分析结果
Fig. 7 Result of oscillation analysis of control bandwidth of the sending MMC
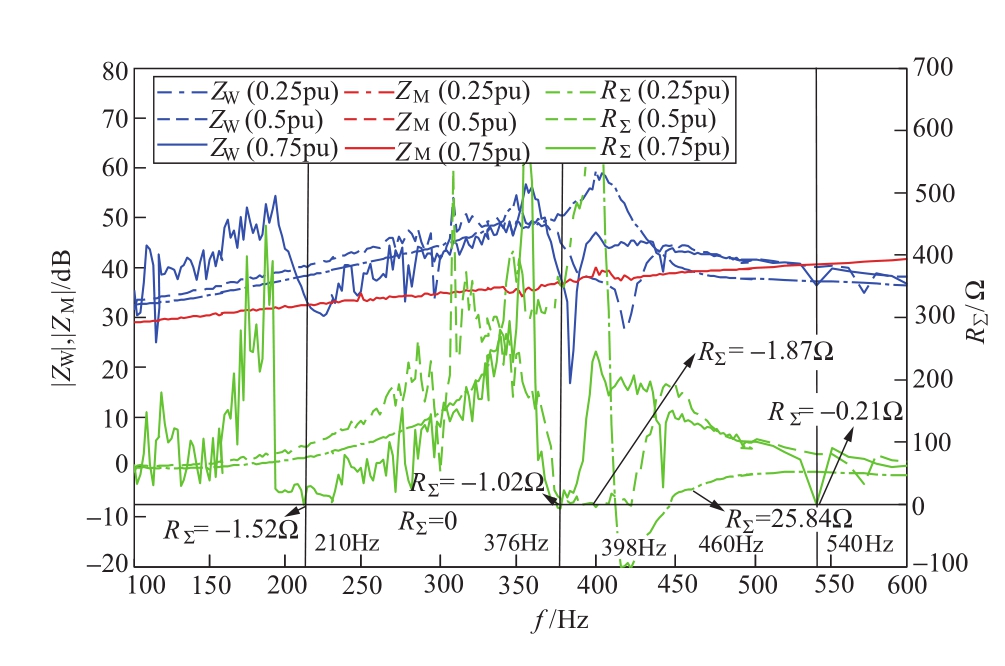
图8 风机出力对等效电路阻尼特性的影响
Fig. 8 Influence of wind power on network damping characteristics
4 风速和并网风机台数影响因素
风速与并网风机台数的不同将导致系统运行在不同的工作点,会改变控制系统引发功率振荡的影响。
4.1 风速
风速的变化影响风机出力的大小。当风机出力逐渐增大时,利用等效电路阻尼稳定性判据,对一定控制参数设定下的互联系统进行分析,如图8所示。可见,当出力增大至0.5 pu时,系统开始在398 Hz出现呈负阻尼特性的谐振点,存在振荡风险。当出力增大至0.75 pu时,可能出现振荡的频率增多,潜在的系统振荡愈发复杂。而风机出力减小至0.25 pu时系统无潜在振荡风险。因此,风机出力越大,系统稳定对风机与柔直互联系统控制参数的设计要求越高。
4.2 风机台数
当接入的风机台数逐渐增多时,利用等效电路阻尼稳定性判据,对一定控制参数设定下的互联系统进行分析,如图9所示。可见,风机台数的增多至900~1000台时,系统开始在谐振点呈现负阻尼,具有振荡风险。而风机减少至800台时,系统无潜在振荡风险。因此,风场台数越多,系统稳定对风机与柔直互联系统控制参数的设定要求越高。
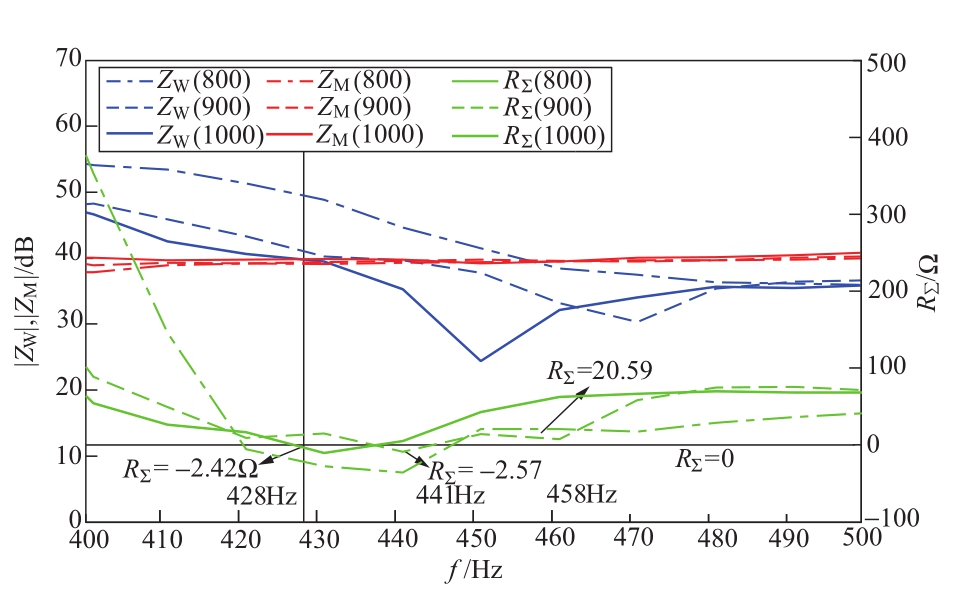
图9 风机台数对等效电路阻尼特性的影响
Fig. 9 Influence of wind turbines number on network damping characteristics
根据风机出力和风机台数对互联系统稳定性的影响,风电场满出力时对控制系统参数设计要求最高,故考虑互联系统稳定性问题,风机网侧变流器控制带宽、锁相环控制带宽以及送端MMC控制带宽的设计应以风电场满出力为前提条件。
5 结论
本文以双馈风电场经MMC-HVDC并网系统为研究对象,推导了基于等效电路阻尼的互联系统稳定性判据,通过调节不同控制比例增益来改变控制带宽,分析了振荡风险与控制系统的关系以及风速与并网风机台数的影响,主要结论如下。
1)风机网侧变流器控制带宽过窄会引发次/超同步频率范围的振荡,且振荡频率随比例增益变小而远离基频;风机网侧变流器控制带宽过宽会引发中高频范围的振荡,且振荡频率随比例增益变大而增大。
2)风机锁相环控制带宽过宽会在次/超同步频率范围内产生负阻尼的谐振点,且振荡频率随比例增益变大而远离基频。
3)送端MMC控制带宽过窄时会在次同步频率范围内产生负阻尼的谐振点,而带宽过宽时在次同步频率和中高频范围均可能存在振荡风险。
4)风机出力越大或并网风机台数越多,互联系统振荡风险越大,对风机与柔性直流控制参数的设计要求越高,控制参数设计应考虑风场满出力工况。
参考文献
[1] Debnath S, Qin J, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter: a review[J].IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.
[2] 赵岩,郑斌毅,贺之渊等.南汇柔性直流输电示范工程的控制方式和运行性能[J].南方电网技术,2012,(6):6-10.ZHAO Yan, ZHENG Binyi, HE Zhiyuan, et al. The control mode and operating performance of Nanhui VSC-HVDC demonstration project [J]. Southern Power System Technology,2012, (6): 6-10 (in Chinese).
[3] 魏伟,许树楷,李岩,等.南澳多端柔性直流输电示范工程系统调试[J].南方电网技术,2015,(1):73-77.WEI Wei, XU Shukai, LI Yan, et al. The system commissioning of Nan’ao VSC-MTDC demonstration project[J]. Southern Power System Technology, 2015, (1): 73-77 (in Chinese).
[4] Buchhagen C, Rauscher C, Menze A, et al. BorWin1-First Experiences with harmonic interactions in converter dominated grids[C]//International ETG Congress 2015; Die Energiewende-Blueprints for the new energy age; Proceedings of VDE, 2016: 1-7.
[5] 姜齐荣,王亮,谢小荣.电力电子化电力系统的振荡问题及其抑制措施研究[J].高电压技术,2017,43(4):1057-1066.JIANG Qirong, WANG Liang, XIE Xiaorong. Study on oscillations of power-electronized power system and their mitigation schemes[J]. High Voltage Engineering, 2017, 43(4):1057-1066 (in Chinese).
[6] 李明节,于钊,许涛,等.新能源并网系统引发的复杂振荡问题及其对策研究[J].电网技术,2017,41(4): 1035-1042.LI Mingjie, YU Zhao, XU Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042 (in Chinese).
[7] 吕敬,董鹏,施刚,等.大型双馈风电场经MMC-HVDC并网的次同步振荡及其抑制[J].中国电机工程学报,2015,35(19):4852-4860.LYU Jing, DONG Peng, SHI Gang, et al. Subsynchronous oscillation and its mitigation of MMC-based HVDC with large doubly-fed induction generator-based wind farm integration[J].Proceedings of the CSEE, 2015, 35(19): 4852-4860 (in Chinese).
[8] 陈润泽,吴文传,孙宏斌,等.双馈风电机组惯量控制对系统小干扰稳定的影响[J].电力系统自动化,2014(23):6-12.CHEN Runze, WU Wenchuan, SUN Hongbin, et al. Impact of inertia control of DFIG wind turbines on system small-signal stability[J]. Automation of Electric Power Systems, 2014,38(23): 6-12 (in Chinese).
[9] LI T, Gole A M, Zhao C. Harmonic Instability in MMCHVDC Converters Resulting From Internal Dynamics[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1738-1747.
[10] Cespedes M, Sun J. Impedance modeling and analysis of gridconnected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[11] SUN J. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011,26(11): 3075-3078.
[12] Amin M, Molinas M. Small-signal Stability Assessment of Power Electronics based Power Systems: A Discussion of Impedance- and Eigenvalue-based Methods[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 5014-5030.
[13] LIU H, SUN J. Voltage Stability and Control of Offshore Wind Farms With AC Collection and HVDC Transmission[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics,2014, 2(4): 1181-1189.
[14] Amin M, Molinas M. Understanding the Origin of Oscillatory Phenomena Observed between Wind Farms and HVDC Systems[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(1): 378-392.
[15] LYU J, CAI X, Molinas M. Frequency Domain Stability Analysis of MMC-Based HVdc for Wind Farm Integration[J].IEEE Journal of Emerging & Selected Topics in Power Electronics, 2016, 4(1): 141-151.
[16] SUN J, LIU H. Sequence Impedance Modeling of Modular Multilevel Converters[J]. IEEE Journal of Emerging &Selected Topics in Power Electronics, 2017, 5(4): 1427-1443.
[17] 杨洪雨.双馈异步发电机系统阻抗建模及稳定性分析[D],浙江大学,2016.
[18] 谢小荣,刘华坤,贺静波,等.新能源发电并网系统的小信号阻抗/导纳网络建模方法[J].电力系统自动化,2017,41(12):26-32.XIE Xiaorong, LIU Huakun, HE Jingbo, et al. Small-signal impedance/admittance network modeling for grid-connected renewable energy generation systems[J]. Automation of Electric Power Systems, 2017, 41(12): 26-32 (in Chinese).
[19] 李英彪,卜广全,王姗姗,等.张北柔直电网工程直流线路短路过程中直流过电压分析[J].中国电机工程学报,2017,37(12):3391-3399.LI Yingbiao, BU Guangquan, WANG Shanshan, et al.Analysis of DC overvoltage caused by DC short-circuit fault in Zhangbei VSC-Based DC grid[J]. Proceedings of the Csee,2017, 37(12): 3391-3399 (in Chinese).
Analysis of Risk and Impacting Factors of Oscillation in Wind Farms Integration via a Flexible HVDC System Based on Equivalent Circuit Damping Stability Criterion
WANG Xiao1,2, LIU Hui1,2, HU Xiao-bao1,3, LAN Hai-bo4, WU Lin-lin1,2
(1. State Grid Jibei Electric Power Co. Ltd. Research Institute, North China Electric Power Research Institute Co. Ltd., Xicheng District,Beijing 100045, China; 2. State Grid Wind-Solar-Energy Storage Generation Laboratory, Xicheng District, Beijing 100045, China;3. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071051, Hebei Province, China;4. State Grid Jibei Electric Power Company Limited, Xicheng District, Beijing 100054, China)
Abstract: Flexible HVDC technology is widely used in largescale wind power transmission, but oscillation phenomena might occur due to the interaction of power electronic devices. Firstly,on the basis of impedance analysis, the stability criterion of interconnection system based on equivalent circuit damping is derived to explain the mechanism of oscillation in the physical sense clearly. Secondly, combining this criterion and time domain simulation, the relationship between oscillation risk and the control bandwidth of wind turbines or flexible HVDC converter control system is analyzed, and variation of oscillation frequency with the change of control parameters is pointed out. Finally, the influence of wind speed and wind turbines number on network damping characteristics of wind farms integration via a flexible HVDC system is analyzed, and the design requirement of control parameters for oscillation stability constraints is proposed.
Key words: wind power; flexible HVDC; stability; oscillation;influencing factor
Project Supported by National Key Research and Development Program of China (2016YFB0900500) and Science and Technology Foundation of SGCC (5201011600 UC).
作者简介:

王潇
王潇(1987),男,博士,研究方向为新能源并网技术,E-mail:wangxiao2017@foxmail.com。
刘辉(1975),男,博士,教授级高级工程师,主要从事新能源并网相关技术研究工作。
(责任编辑 张鹏)
